Command Palette
Search for a command to run...
Coupling Experts and Routers in Mixture-of-Experts via an Auxiliary Loss
Coupling Experts and Routers in Mixture-of-Experts via an Auxiliary Loss
Ang Lv Jin Ma Yiyuan Ma Siyuan Qiao
Abstract
Mixture-of-Experts (MoE) models lack explicit constraints to ensure the router's decisions align well with the experts' capabilities, which ultimately limits model performance. To address this, we propose expert-router coupling (ERC) loss, a lightweight auxiliary loss that tightly couples the router's decisions with expert capabilities. Our approach treats each expert's router embedding as a proxy token for the tokens assigned to that expert, and feeds perturbed router embeddings through the experts to obtain internal activations. The ERC loss enforces two constraints on these activations: (1) Each expert must exhibit higher activation for its own proxy token than for the proxy tokens of any other expert. (2) Each proxy token must elicit stronger activation from its corresponding expert than from any other expert. These constraints jointly ensure that each router embedding faithfully represents its corresponding expert's capability, while each expert specializes in processing the tokens actually routed to it. The ERC loss is computationally efficient, operating only on n^2 activations, where n is the number of experts. This represents a fixed cost independent of batch size, unlike prior coupling methods that scale with the number of tokens (often millions per batch). Through pre-training MoE-LLMs ranging from 3B to 15B parameters and extensive analysis on trillions of tokens, we demonstrate the effectiveness of the ERC loss. Moreover, the ERC loss offers flexible control and quantitative tracking of expert specialization levels during training, providing valuable insights into MoEs.
One-sentence Summary
The authors from Renmin University of China and ByteDance Seed propose a lightweight expert-router coupling (ERC) loss that enforces alignment between router decisions and expert capabilities by using perturbed router embeddings as proxy tokens, ensuring each expert specializes in its assigned tokens through dual activation constraints—outperforming prior methods in computational efficiency and enabling fine-grained tracking of expert specialization in MoE-LLMs up to 15B parameters.
Key Contributions
- Mixture-of-Experts (MoE) models suffer from weak alignment between router decisions and expert capabilities, leading to suboptimal token routing and hindered specialization, which limits overall performance despite their efficiency advantages.
- The proposed expert-router coupling (ERC) loss introduces a lightweight, n2-cost auxiliary loss that enforces two key constraints: each expert must activate more strongly on its own proxy token (derived from perturbed router embeddings) than on others, and each proxy token must activate its corresponding expert most strongly, thereby tightly coupling router representations with expert capabilities.
- Extensive pre-training on 3B to 15B parameter MoE-LLMs using trillions of tokens demonstrates that ERC loss improves downstream performance while maintaining low training overhead, and enables quantitative tracking and flexible control of expert specialization levels during training.
Introduction
The authors address a key limitation in Mixture-of-Experts (MoE) language models: the weak coupling between router decisions and expert capabilities, which can lead to suboptimal expert utilization and hinder model performance. This decoupling often results in poor specialization and inefficient resource allocation during inference. To overcome this, the authors introduce an expert-router coupling (ERC) loss that tightly aligns router parameters with their corresponding experts during training. The ERC loss enhances downstream task performance with minimal additional training cost and provides deeper insights into expert specialization, offering a valuable tool for future MoE model research.
Method
The authors leverage a novel auxiliary loss, termed expert-router coupling (ERC) loss, to address the lack of explicit constraints ensuring alignment between router decisions and expert capabilities in Mixture-of-Experts (MoE) models. The core of the ERC loss is a three-step process that operates on the router's parameter matrix, treating each row as a cluster center representing a token cluster routed to a specific expert. This framework is illustrated in the accompanying diagram.

The first step involves generating a perturbed proxy token for each expert. Specifically, each router parameter vector R[i] is augmented with bounded random noise δi to produce a proxy token R~[i]=R[i]⊙δi. This noise is modeled as a multiplicative uniform distribution, ensuring the proxy token generalizes to the tokens assigned to its corresponding expert while remaining within the same cluster. The second step processes each of these n proxy tokens through all n experts. The intermediate activation norm from each expert j given input R~[i] is computed, forming an n×n matrix M, where M[i,j]=∥R~[i]⋅Wgj∥. This step is designed to be computationally efficient, operating on n2 activations, which is independent of the batch size.
The third and final step enforces expert-router coupling by applying two constraints to the matrix M. For all i=j, the loss penalizes cases where the activation norm from expert j to proxy i exceeds a scaled version of the activation norm from expert i to its own proxy, and vice versa. This is formalized as M[i,j]<αM[i,i] and M[j,i]<αM[i,i], where α is a scalar hyperparameter. The overall ERC loss is the mean of the positive parts of these violations, defined as:
LERC=n21i=1∑nj=i∑n(max(M[i,j]−αM[i,i],0)+max(M[j,i]−αM[i,i],0)).Minimizing this loss ensures that each expert exhibits its highest activation for its own proxy token (promoting expert specialization) and that each proxy token elicits its strongest activation from its corresponding expert (ensuring precise token routing). The ERC loss is designed to be lightweight, with a fixed computational cost of 2n2Dd FLOPs, and does not introduce activation density beyond that of a vanilla MoE, making it a practical and efficient enhancement. The authors also demonstrate that the ERC loss provides a quantitative measure of expert specialization, as the hyperparameter α directly controls the degree of specialization.
Experiment
- ERC-loss-augmented MoE outperforms vanilla MoE and narrows the gap with AoE on multiple benchmarks, achieving significant and stable gains across tasks including ARC-Challenge, CommonsenseQA, MMLU, and others, with consistent improvements on both 3B and 15B parameter models.
- On the 3B model, ERC loss achieves comparable load balancing to vanilla MoE (difference ~10⁻⁵) and maintains near-identical training throughput and memory usage, while AoE incurs 1.6× higher training time and 1.3× higher memory usage, making it impractical for scaling.
- The ERC loss introduces negligible overhead—0.2–0.8% in real-world distributed training—due to its low FLOP cost (0.18–0.72% of base forward pass), confirmed by both theoretical analysis and empirical throughput measurements.
- ERC loss enables effective expert specialization, as shown by t-SNE visualizations and quantitative metrics: increased clustering in expert parameters and a measurable correlation between the noise level ε and specialization degree controlled by α.
- Ablation studies confirm that the random noise δ in the ERC loss is critical for generalization, and the loss cannot be replaced by separate constraints on routers or experts (e.g., router orthogonality), which yield limited gains even when router embeddings are already nearly orthogonal.
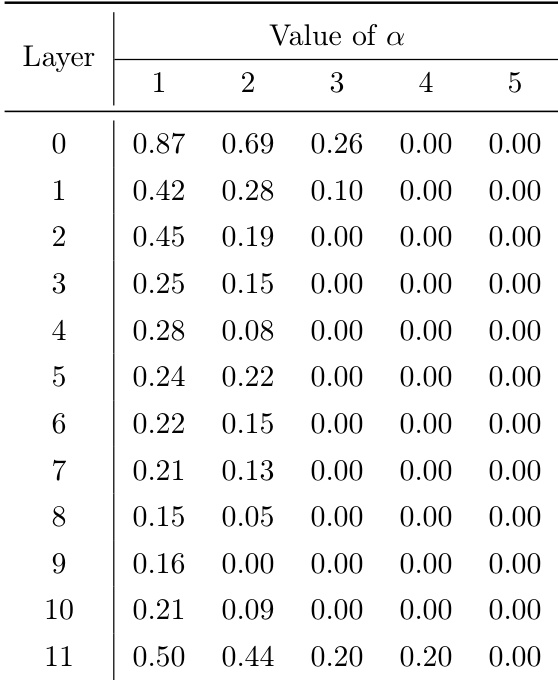
- The optimal specialization level is not extreme; performance degrades with overly strict α, indicating a trade-off between specialization and collaboration, with optimal α depending on model scale (e.g., α=1 for n=64, α=0.5 for n=256).
- ERC loss is effective at scale: on 15B models with n=256 and K=8, it improves performance across challenging benchmarks including MMLU-Pro, AGI-Eval, MATH, and GSM8K, despite AoE failing to train due to excessive cost.
The authors use the ERC loss to strengthen the coupling between routers and experts in a MoE model, and the table shows that this results in a significant reduction of the ERC loss across all layers, with values dropping to 0.00 when the loss is applied. This indicates that the model learns to align router and expert parameters effectively, as evidenced by the near-zero ERC loss in the +LERC column, while the baseline values remain non-zero.
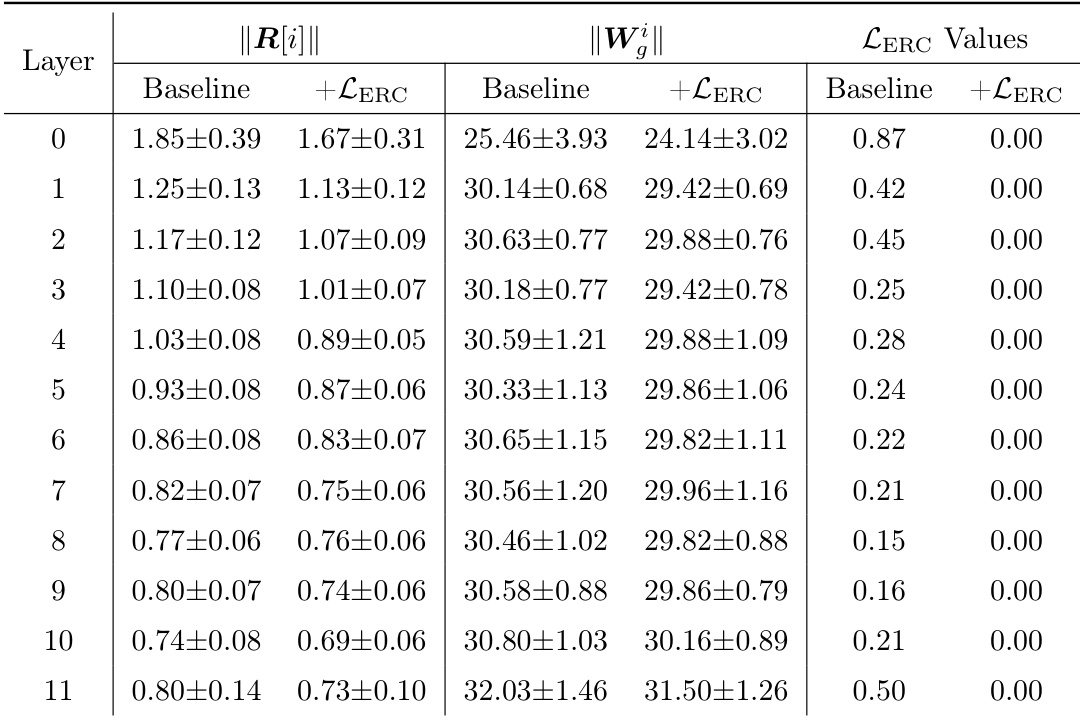
The authors use the ERC loss to investigate expert specialization by varying the coupling strength parameter α, and the table shows that as α increases, the ERC loss decreases across all layers, indicating reduced specialization. This trend is consistent with the analysis that higher α values weaken the coupling constraint, leading to more homogeneous experts and lower performance gains.
The authors use the ERC loss to enhance expert-router coupling in MoE models, resulting in consistent performance improvements across multiple benchmarks. Results show that the MoE model augmented with ERC loss achieves higher accuracy than the vanilla MoE baseline, with gains observed in both 3B and 15B parameter models, while maintaining low computational overhead and effective load balancing.
