One-sentence Summary

The authors propose a novel attention-free sequence model based on Grassmann flows, leveraging low-rank subspace dynamics on Gr(2, r) and Plücker embeddings to enable geometric, linearly scalable information fusion—achieving competitive performance on language modeling and natural inference tasks while offering a more analytically tractable alternative to dense self-attention.

Key Contributions

• The paper challenges the assumption that dense or approximate self-attention is essential for strong language modeling, reframing attention as a high-dimensional tensor lifting operation that obscures model behavior due to its analytical intractability across layers and heads.

• It introduces a novel attention-free architecture based on Grassmann flows, where local token pairs are modeled as 2D subspaces on a Grassmann manifold Gr(2, r), embedded via Plücker coordinates and fused through a gated mixing block, enabling geometric evolution of hidden states without explicit pairwise weights.

• Evaluated on Wikitext-2 and SNLI, the Grassmann-based model achieves competitive performance—within 10–15% of a Transformer baseline in perplexity and slightly better accuracy in classification—while offering linear complexity in sequence length for fixed rank, contrasting with the quadratic cost of self-attention.

Introduction

The authors challenge the foundational role of self-attention in sequence modeling, which has become the default mechanism in Transformers due to its expressiveness and parallelizability. While prior work has focused on optimizing attention—reducing its quadratic complexity through sparsification, approximation, or memory augmentation—these approaches still rely on computing or approximating an $L \times L$L×L attention matrix. The key limitation is that attention is treated as indispensable, despite being just one way to implement geometric lifting of representations. The authors propose Grassmann flows as a fundamentally different alternative: instead of pairwise interactions via attention, they model sequence dynamics through the evolution of subspaces on a Grassmann manifold, using Plücker coordinates to encode geometric relationships. This approach eliminates the need for explicit attention entirely, offering a geometry-driven mechanism for sequence modeling that is both mathematically principled and computationally efficient. Their main contribution is integrating this Grassmann–Plücker pipeline into a Transformer-like architecture, demonstrating that geometric mixing can replace attention while preserving strong performance, with potential for future extensions incorporating global invariants.

Dataset

• The dataset used is Wikitext-2-raw, a widely adopted benchmark for language modeling tasks.
• Text sequences are created by splitting the raw text into contiguous chunks of fixed length, with block sizes of either 128 or 256 tokens.
• A WordPiece-like vocabulary of approximately 30,522 tokens is employed, consistent with BERT-style tokenization.
• The authors compare two model architectures: TransformerLM, a standard decoder-only Transformer, and GrassmannLM, which replaces each self-attention block with a Causal Grassmann mixing block.
• Two model depths are evaluated: Shallow (6 layers) and Deeper (12 layers), with both models maintaining identical embedding dimensions (d=256), feed-forward dimensions (d_ff=1024), and 4 attention heads.
• For GrassmannLM, a reduced dimension of r=32 is used, and multi-scale window patterns are applied: {1, 2, 4, 8, 12, 16} for the 6-layer model, and a repeated pattern (1, 1, 2, 2, 4, 4, 8, 8, 12, 12, 16, 16) across layers for the 12-layer model.
• Both models are trained for 30 epochs using the same optimizer and learning rate schedule, differing only in the mixing block type.
• Best validation perplexity is reported across training, with batch sizes of 32 for L=128 and 16 for L=256.

Method

The authors leverage a geometric reinterpretation of self-attention to propose an alternative sequence modeling framework that replaces the standard attention mechanism with a structured, attention-free process based on Grassmann flows. This approach rethinks the core interaction mechanism in sequence models by shifting from unstructured tensor lifting to a controlled geometric evolution on a finite-dimensional manifold. The overall architecture, referred to as the Causal Grassmann Transformer, follows the general structure of a Transformer encoder but substitutes each self-attention block with a Causal Grassmann mixing layer. This layer operates by reducing the dimensionality of token representations, encoding local pairwise interactions as geometric subspaces on a Grassmann manifold, and fusing the resulting features back into the hidden state space through a gated mechanism.

The process begins with token and positional embeddings, where input tokens are mapped to a $d$d-dimensional space using a learned embedding matrix and augmented with positional encodings. This initial sequence of hidden states is then processed through $N$N stacked Causal Grassmann mixing layers. Each layer performs a sequence of operations designed to capture local geometric structure without relying on explicit pairwise attention weights. First, a linear reduction step projects each hidden state $h_t \in \mathbb{R}^d$ht​∈Rd into a lower-dimensional space via $z_t = W_{\text{red}} h_t + b_{\text{red}}$zt​=Wred​ht​+bred​, resulting in $Z \in \mathbb{R}^{L \times r}$Z∈RL×r, where $r \ll d$r≪d. This reduction step serves to compress the representation while preserving essential local information.

As shown in the figure below, the framework proceeds by constructing local pairs of reduced states $(z_t, z_{t+\Delta})$(zt​,zt+Δ​) for a set of multi-scale window sizes $\mathcal{W}$W, such as $\{1, 2, 4, 8, 12, 16\}${1,2,4,8,12,16}, ensuring causality by only pairing each position $t$t with future positions. For each such pair, the authors interpret the span of the two vectors as a two-dimensional subspace in $\mathbb{R}^r$Rr, which corresponds to a point on the Grassmann manifold $\text{Gr}(2, r)$Gr(2,r). This subspace is encoded using Plücker coordinates, which are derived from the exterior product of the two vectors. Specifically, the Plücker vector $p_t^{(\Delta)} \in \mathbb{R}^{\binom{r}{2}}$pt(Δ)​∈R(2r​) is computed as $p_{ij}^{(\Delta)}(t) = z_{t,i} z_{t+\Delta,j} - z_{t,j} z_{t+\Delta,i}$pij(Δ)​(t)=zt,i​zt+Δ,j​−zt,j​zt+Δ,i​ for $1 \leq i < j \leq r$1≤i<j≤r. These coordinates represent the local geometric structure of the pair in a finite-dimensional projective space, subject to known algebraic constraints.

The Plücker vectors are then projected back into the model's original dimensionality through a learned linear map $g_t^{(\Delta)} = W_{\text{plü}} \hat{p}_t^{(\Delta)} + b_{\text{plü}}$gt(Δ)​=Wplu¨​p^​t(Δ)​+bplu¨​, where $\hat{p}_t^{(\Delta)}$p^​t(Δ)​ is a normalized version of the Plücker vector for numerical stability. The resulting features are aggregated across all valid offsets at each position $t$t to form a single geometric feature vector $g_t$gt​. This vector captures multi-scale local geometry and is fused with the original hidden state $h_t$ht​ via a gated mechanism. The gate $\alpha_t$αt​ is computed as $\sigma(W_{\text{gate}} [h_t; g_t] + b_{\text{gate}})$σ(Wgate​[ht​;gt​]+bgate​), and the mixed representation is given by $\tilde{h}_t^{\text{mix}} = \alpha_t \odot h_t + (1 - \alpha_t) \odot g_t$h~tmix​=αt​⊙ht​+(1−αt​)⊙gt​. This fusion step allows the model to adaptively combine the original representation with the geometric features.

Following the gated fusion, the representation undergoes layer normalization and dropout. A position-wise feed-forward network, consisting of two linear layers with a GELU nonlinearity and residual connections, further processes the hidden states. The output of this block is normalized and serves as the updated hidden state for the next layer. This entire process is repeated across $N$N layers to form the full Causal Grassmann Transformer.

The key distinction from standard self-attention lies in the absence of an $L \times L$L×L attention matrix and the associated quadratic complexity. Instead of computing pairwise compatibility scores across all token positions, the model operates on a finite-dimensional manifold with controlled degrees of freedom. The complexity of the Grassmann mixing layer scales linearly in sequence length for fixed rank $r$r and window size $m$m, in contrast to the quadratic scaling of full self-attention. This linear scaling arises because the dominant cost is the $O(Ld^2)$O(Ld2) term from the feed-forward network and linear operations, while the Plücker computation and projection contribute $O(Lmr^2)$O(Lmr2), which is subdominant for fixed $r$r and $m$m. The authors argue that this shift from tensor lifting to geometric flow provides a more interpretable and analytically tractable foundation for sequence modeling, as the evolution of the model's behavior can be studied as a trajectory on a well-defined manifold rather than a composition of high-dimensional, unstructured tensors.

Experiment

• On Wikitext-2 language modeling, GrassmannLM achieves validation perplexity of 275.7 (6-layer) and 261.1 (12-layer), remaining within 10–15% of size-matched TransformerLMs despite using no attention, with the gap narrowing at greater depth.
• On SNLI natural language inference with a DistilBERT backbone, the Grassmann-Plücker head achieves 85.50 validation and 85.38 test accuracy, slightly outperforming the Transformer head (85.45 validation, 85.11 test).
• The Grassmann architecture demonstrates viability as an attention-free sequence model, with comparable parameter counts and consistent performance across settings, validating that geometrically structured local mixing can support semantic reasoning.
• Empirical runtime remains slower than Transformer baseline due to unoptimized implementation, though theoretical complexity is linear in sequence length, indicating potential for future scaling gains with specialized optimization.

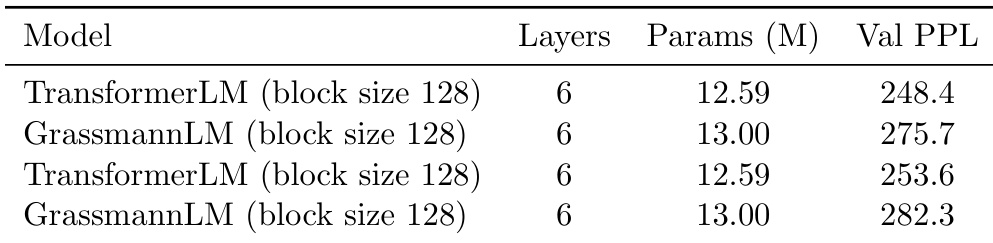
The authors use the table to compare the performance of TransformerLM and GrassmannLM on the Wikitext-2 language modeling task under identical conditions. Results show that the GrassmannLM achieves higher validation perplexity than the TransformerLM, with values of 275.7 and 282.3 compared to 248.4 and 253.6, respectively, indicating that the Grassmann model performs worse despite having slightly more parameters.

The authors use a 12-layer model with block size 256 to compare TransformerLM and GrassmannLM on language modeling. Results show that GrassmannLM achieves a validation perplexity of 261.1, which is higher than the TransformerLM's 235.2, indicating a performance gap under these conditions.

The authors use a DistilBERT backbone with two different classification heads—Transformer and Grassmann-Plücker—to evaluate performance on the SNLI natural language inference task. Results show that the Grassmann-Plücker head achieves slightly higher validation and test accuracy compared to the Transformer head, indicating that explicit geometric structure in the classification head can improve performance on downstream reasoning tasks.