Command Palette
Search for a command to run...
Lernmodelle, die sich selbst beibringen: Schlussfolgern am Rande der Lernbarkeit
Lernmodelle, die sich selbst beibringen: Schlussfolgern am Rande der Lernbarkeit
Shobhita Sundaram John Quan Ariel Kwiatkowski Kartik Ahuja Yann Ollivier Julia Kempe
Zusammenfassung
Kann ein Modell lernen, aus seiner eigenen Lernplatte zu entkommen? Verstärkendes Lernen zur Feinabstimmung großer Schlussfolgerungsmodelle gerät bei Datensätzen mit niedrigen Ausgangserfolgsraten ins Stocken, da hier nur wenig Trainingssignal verfügbar ist. Wir untersuchen eine grundlegende Frage: Kann ein vortrainiertes Sprachmodell latente Kenntnisse nutzen, um einen automatisierten Lehrplan für Probleme zu generieren, die es selbst nicht lösen kann? Um dies zu erforschen, entwickeln wir SOAR: Ein Selbstverbesserungsframework, das durch Meta-Verstärkendes Lernen (Meta-RL) diese pädagogischen Signale aufzudecken versucht. Eine Lehrer-Kopie des Modells schlägt synthetische Aufgaben für eine Schüler-Kopie vor und wird belohnt, basierend auf deren Verbesserung bei einer kleinen Teilmenge schwieriger Probleme. Entscheidend ist, dass SOAR den Lehrplan nicht auf willkürliche, intrinsische Belohnungsschemata stützt, sondern auf gemessenen Fortschritt des Schülers. Unsere Studie an den anspruchsvollsten Teilgruppen mathematischer Benchmark-Datensätze (0/128 Erfolgsrate) ergibt drei zentrale Erkenntnisse. Erstens zeigen wir, dass es möglich ist, ein zweistufiges Meta-RL-Verfahren zu realisieren, das Lernen unter spärlichen, binären Belohnungen ermöglicht, indem die latente Fähigkeit vortrainierter Modelle zur Generierung nützlicher Zwischenschritte geschärft wird. Zweitens übertrifft der durch den Lernfortschritt des Schülers fundierte Belohnungsansatz die in früheren Arbeiten zu LLM-Selbstspiel verwendeten intrinsischen Belohnungsschemata, indem er stabilere und diversitätsstabile Lernprozesse gewährleistet. Drittens zeigt die Analyse der generierten Fragen, dass strukturelle Qualität und korrekte Problemformulierung für den Lernfortschritt entscheidender sind als die Korrektheit der Lösung. Unsere Ergebnisse deuten darauf hin, dass die Fähigkeit, nützliche Zwischenschritte zu generieren, nicht voraussetzt, dass das Modell die schwierigen Probleme bereits lösen kann – dies eröffnet einen prinzipiengeleiteten Weg, um aus Lernplattauen in Schlussfolgerungsmodellen auszubrechen, ohne zusätzliche, manuell kuratierte Daten zu benötigen.
One-sentence Summary
MIT and Meta FAIR researchers propose SOAR, a meta-RL framework enabling LLMs to generate self-curated curricula for unsolvable problems by grounding teacher rewards in student progress, not intrinsic signals, thereby escaping reasoning plateaus without curated data.
Key Contributions
- SOAR introduces a bi-level meta-RL framework that enables pretrained LLMs to generate synthetic curricula for hard problems they initially cannot solve, using grounded rewards based on measurable student improvement rather than intrinsic proxies.
- On math benchmarks with near-zero initial success (0/128), SOAR reliably avoids the instability and collapse seen in prior self-play methods by anchoring teacher rewards to real performance gains, not self-consistency or solution quality.
- Analysis shows that structural quality and well-posedness of generated problems drive learning more than solution correctness, demonstrating that useful stepping stones can emerge without prior solving ability.
Introduction
The authors tackle a core limitation in fine-tuning large language models for reasoning: when initial success rates are near zero, reinforcement learning with verifiable rewards (RLVR) fails due to sparse signals. Prior self-play and curriculum methods rely on intrinsic or proxy rewards—like self-consistency or gradient norms—which often collapse into degenerate or unlearnable tasks, especially in symbolic domains with binary correctness. The authors introduce SOAR, a meta-RL framework where a teacher model generates synthetic problems for a student model, and is rewarded only when the student improves on a small set of real hard problems. This grounded, bilevel approach avoids reward hacking and enables learning even when the model cannot initially solve the target problems, revealing that latent knowledge can be surfaced through self-generated stepping stones without human curation.
Dataset
-
The authors use three math reasoning benchmarks—MATH, HARP, and OlympiadBench—to study sparse binary rewards in settings without automatic verification. These cover problems from AMC, AIME, USA(J)MO, and international Olympiads.
-
For each dataset, they apply a “fail@128” filter: they sample 128 solutions per problem using Llama-3.2-3B-Instruct (with 1024 token budget and temperature 1.0) and retain only problems with 0/128 success rate. This creates a challenging subset where direct training yields minimal gains.
-
OlympiadBench: Uses only the 674 English, text-only, automatically verifiable problems. A random 50-50 train/test split is created since the original was a test set.
-
HARP: Uses the full dataset, and also applies a random 50-50 train/test split for the same reason.
-
MATH: To avoid memorization bias (since Llama-3.2-3B-Instruct shows higher accuracy on MATH’s official train split), they draw the initial problem pool from the 5000-problem official test split. After applying fail@128 filtering, they create their own 50-50 train/test split. All training and evaluation use only this internal split.
-
Dataset sizes: Final train/test splits are reported in Table 2. The test sets are made larger (50% of filtered data) to reliably measure performance gains over stochastic variance.
-
No cropping or metadata construction is mentioned beyond the filtering and splitting. All synthetic data and student-teacher training uses only the internal training splits; final results are evaluated solely on the held-out test splits.
Method
The authors leverage a teacher-student meta-RL framework, termed SOAR, to enable a pretrained language model to generate its own stepping-stone curriculum for solving difficult problems. The framework operates as an asymmetric self-play system where two models, initialized from the same base model, are trained in a nested loop structure. The teacher model, denoted as πϕT, generates synthetic question-answer pairs (q,a)synthetic, which are used to train the student model, πθS. The student's training occurs in an inner loop, where it learns to answer the teacher-generated problems using reinforcement learning. The performance of the student on a set of hard, real-world problems from the target dataset serves as the reward signal for the teacher in the outer loop. This creates a feedback mechanism where the teacher is incentivized to produce synthetic problems that lead to measurable improvement in the student's ability to solve the hard problems, without the teacher ever directly observing these hard problems.
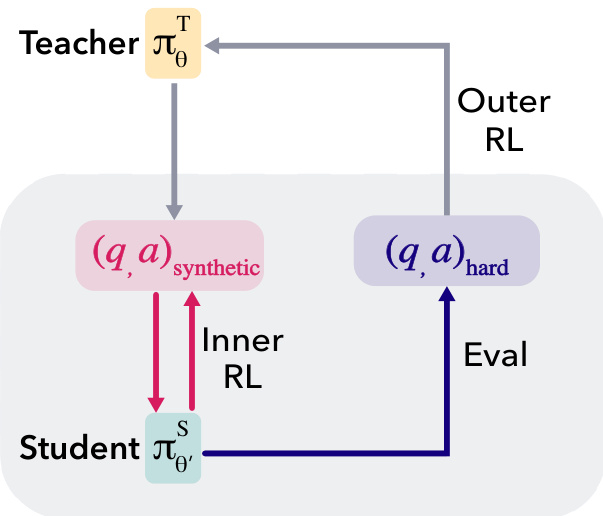
The core of the framework is a bilevel optimization problem, where the objective is to generate a synthetic dataset X that, when used to train the student, maximizes the student's performance on the target domain. To make this computationally feasible, the authors instantiate this objective as a nested meta-RL loop. The outer loop trains the teacher using RLOO (Reinforcement Learning with Out-of-Loop Optimization) to generate synthetic question-answer pairs. The inner loop trains the student using standard RLVR (Reinforcement Learning with Value-based Reward) on the teacher-generated dataset. The key innovation is the grounding of the teacher's reward signal in the student's actual performance on the hard problems, rather than using intrinsic rewards. This black-box reward signal ensures that the teacher is penalized for generating degenerate or unhelpful problems and is rewarded only when the synthetic curriculum leads to genuine learning progress.
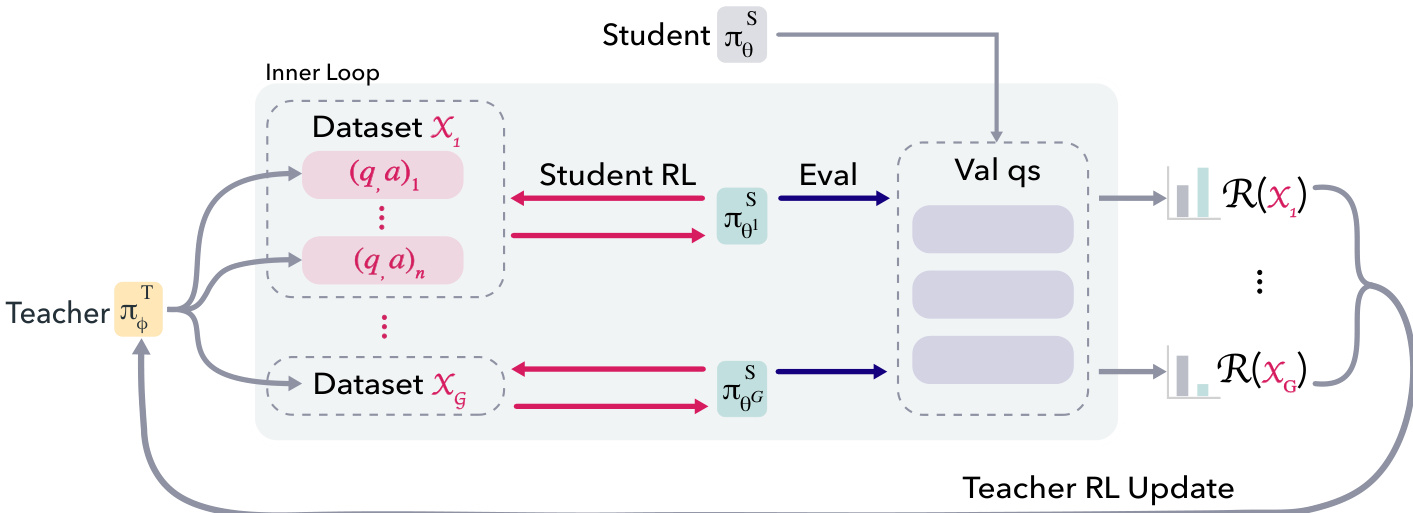
In the outer loop, the teacher generates a batch of g⋅n synthetic question-answer pairs, which are partitioned into g datasets of size n. For each dataset Xk, the inner loop is executed. This involves training the student for a fixed number of steps (10) on Xk and then evaluating the resulting student policy on a subsampled set of hard questions QR from the original training set. The reward for the dataset Xk is the average improvement in the student's success rate on QR compared to a baseline student. To mitigate noise, this reward is averaged over r parallel student trainings. The teacher is then updated using the RLOO algorithm based on these dataset-level rewards.
The inner loop involves training the student on a synthetic dataset Xk using RLOO. The student is trained for a small number of steps to induce measurable policy movement while keeping the computational cost low. After each inner loop, the student reverts to the baseline policy for the next iteration. To address the challenge of the teacher adapting to an improving student, a promotion mechanism is introduced. A moving average of the teacher rewards is tracked, and when it exceeds a fixed threshold τ, the student baseline is reset to the best-performing student policy from the previous iteration. This accumulated dataset, which led to student promotion, is stored as the "Promotion Questions" (PQ) for evaluation.
Experiment
- SOAR trains teacher-student pairs on MATH and HARP (held-out OlympiadBench for OOD testing), using Llama-3.2-3B-Instruct, with 200 outer-loop steps and n=64 samples per iteration; promotes student if 3-step moving average reward exceeds τ=0.01.
- Promoted Student (PS) achieves +8.5% pass@32 on MATH and +3.6% on HARP over Hard-Only; Promotion Questions (PQ) yield +9.3% on MATH and +4.2% on HARP, confirming synthetic questions—not training trajectory—drive gains.
- PQ transfers to OlympiadBench (+6% MATH-PQ, +3% HARP-PQ over Hard-Only), showing cross-dataset generalization despite no OOD optimization.
- PQ recovers 75% of performance gain from full MATH training (6750 problems) and 50% from HARP; HARP-PQ outperforms 128 real HARP questions and matches 128 real MATH questions.
- Grounded-T teachers outperform Intrinsic-T and Base-T, with stable student trajectories and higher diversity (Vendi Score 34.91 vs. 10.82 for Intrinsic-T); Intrinsic-T exhibits high variance and collapse in 1/3 seeds.
- Synthetic questions need not be correct—only 32.8% of PQ problems are fully correct—but structural coherence and diversity matter more; meta-RL reduces ambiguity errors vs. Base-T.
- Hard-Only with 4× compute (group size 128) gains only +2.8% pass@32 on MATH, far below PQ gains.
- Teacher policy itself improves via meta-RL: Grounded-T questions match PQ performance and stabilize student learning curves; promotion mechanism is essential.
- Multi-turn question generation underperforms single-turn; larger sampled datasets (128 vs. 64) from Grounded-T reduce variance without sacrificing mean performance.
- Teacher training follows search-exploitation cycles; grounded rewards preserve diversity while intrinsic rewards collapse it during convergence.
The authors use SOAR to generate synthetic questions that improve student performance on hard problem sets, with results showing that SOAR-PQ and SOAR-PS methods significantly outperform Hard-Only and Intrinsic-T baselines across all pass@k metrics. The best-performing methods, SOAR-PQ (MATH) and SOAR-PS (HARP), achieve pass@32 scores of 12.0 ± 3.0 and 11.7 ± 1.6 respectively, demonstrating that grounded meta-RL effectively discovers useful curricula that enable learning beyond performance plateaus.
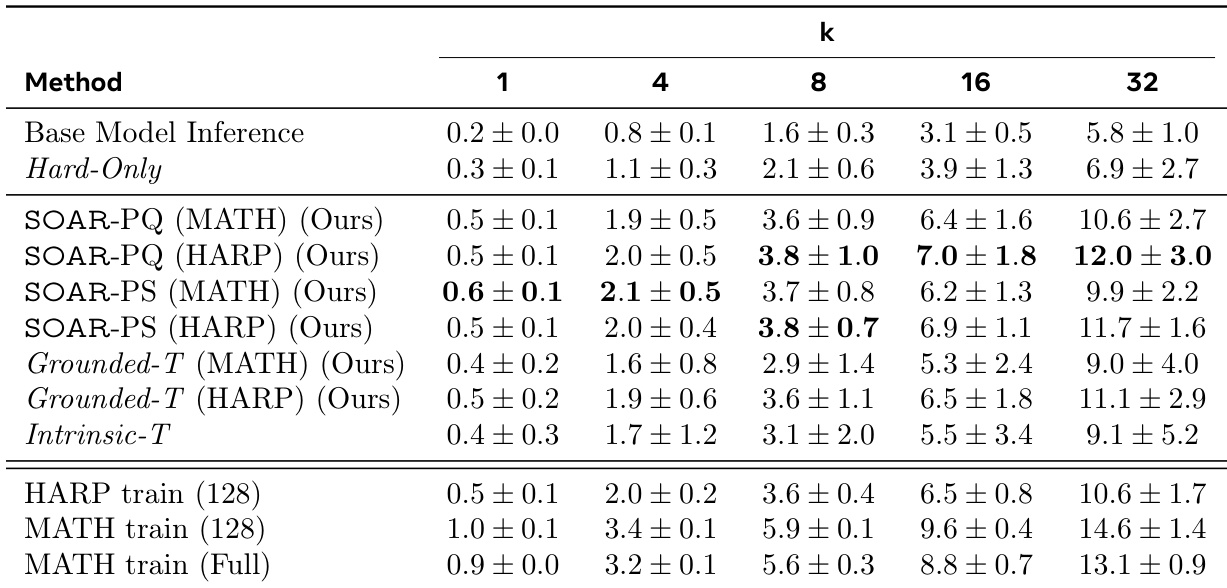
The authors use SOAR to generate synthetic questions that improve student performance on hard problem sets, with results showing that SOAR-PQ and SOAR-PS significantly outperform Hard-Only and Intrinsic-T baselines across all pass@k metrics. The best-performing method, SOAR-PQ, achieves a 19.1% pass@32 accuracy, surpassing even the full MATH train set in some cases, while also demonstrating strong cross-dataset generalization to OlympiadBench.
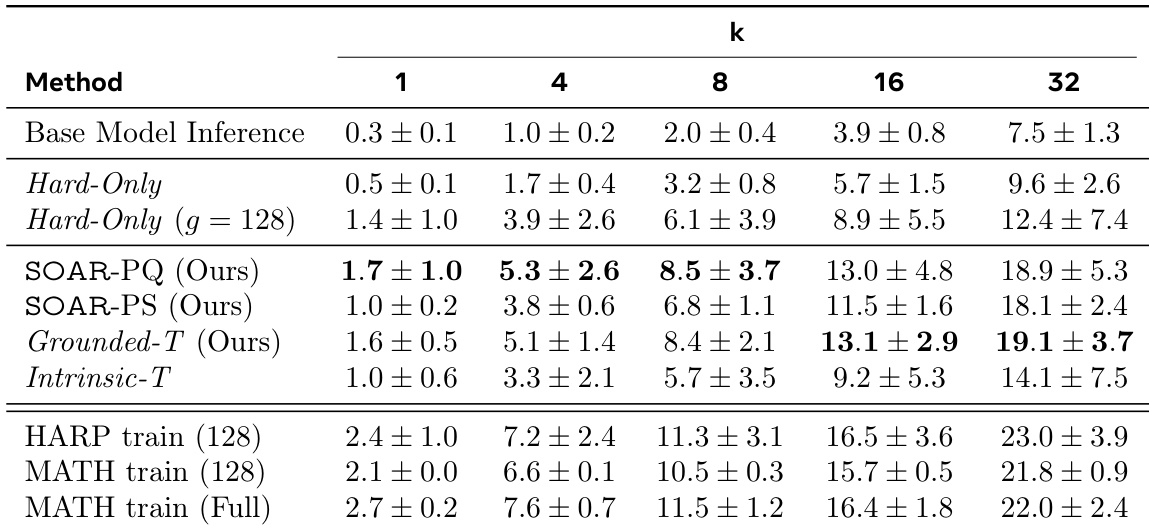
The authors use the table to show the effect of dataset size and number of samples on student performance in the MATH dataset. Results show that increasing the number of samples from 32 to 64 improves performance across all pass@k metrics, while increasing the dataset size from 32 to 128 questions generally leads to lower performance, especially at higher k values.
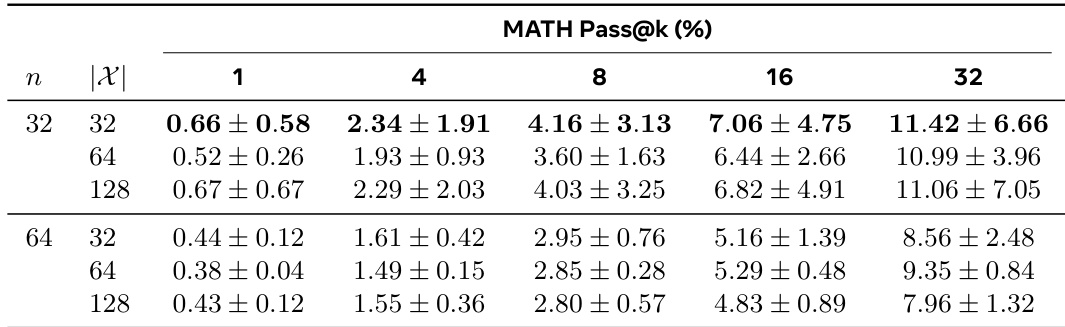
The authors use a table to compare the correctness and error types of synthetic questions generated by different teacher models. Results show that grounded rewards produce questions with higher well-posedness and correctness rates compared to intrinsic and base models, while intrinsic rewards yield the highest correctness but with significantly higher ambiguity and logic errors. The data indicates that question structure and coherence are more important than answer correctness for improving student performance.
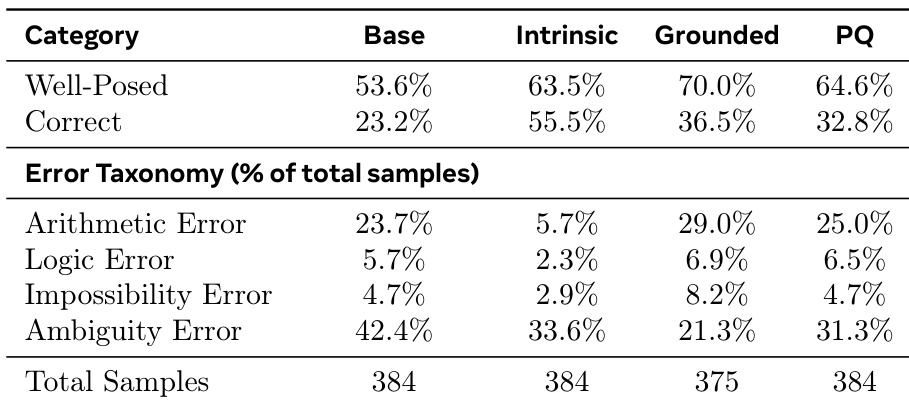
The authors use a meta-RL framework to train a teacher model that generates synthetic problems to improve student performance on hard datasets. Results show that the teacher-generated questions significantly outperform baselines, with the best-performing methods achieving higher pass@k accuracy on MATH and HARP compared to direct training on real data.