Command Palette
Search for a command to run...
Das MIT Entwickelt SCIGEN, Ein Zielgerichtetes Design Für Stabile Materialien, Das Sich an Jedes Vortrainierte Diffusionsmodell Anpassen kann.
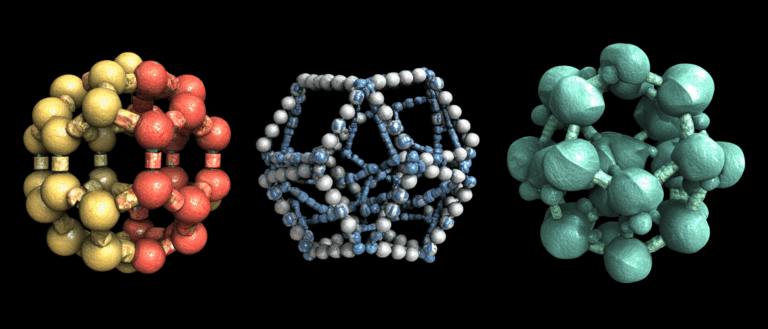
In der Materialwissenschaft existieren die Quanteneigenschaften von Materialien (wie topologische Isolierung, Supraleitung und magnetische Ordnung) nicht isoliert, sondern werden direkt durch strukturelle Eigenschaften wie die Symmetrie ihrer Atomanordnung und Gittergeometrie bestimmt. Dies bietet eine theoretische Grundlage für die gezielte Gestaltung von Quantenmaterialien durch Strukturmanipulation. Der Sprung von der „theoretischen Möglichkeit“ zur „praktischen Nutzbarkeit“ ist jedoch nicht einfach. Aufgrund praktischer Faktoren wie der Komplexität der Strukturmanipulation und des Mangels an relevanten Daten verliefen die Fortschritte bei der Entwicklung stabiler Materialien mit idealen Quanteneigenschaften schleppend. So wurden beispielsweise nach einem Jahrzehnt der Forschung lediglich ein Dutzend Kandidatenmaterialien für Quantenspinflüssigkeiten identifiziert.
Der durch künstliche Intelligenz vorangetriebene wissenschaftliche Paradigmenwechsel verändert die Methoden und Ansätze der Materialentwicklung. Beispielsweise haben gängige Materialgenerierungsmodelle wie CDVAE, UniMat, DiffCSP und GNoME (meist basierend auf Diffusionsmodellen oder Graph-Neural-Network-Architekturen) ein enormes Potenzial bei der Identifizierung stabiler Kristallstrukturen und der Batch-Generierung von Millionen von Materialkandidaten bewiesen.Die meisten Methoden basieren jedoch immer noch auf der Stichprobenziehung aus der statistischen Verteilung der Trainingsdaten, was dazu führt, dass die Ausgabematerialien hinsichtlich der Strukturtopologie und der Leistungsmerkmale auf gängige Typen in vorhandenen Datenbanken beschränkt sind.Kristallographische Raumgruppen liefern jedoch nur einen makroskopischen Strukturrahmen für ein Material und erfassen die entscheidenden lokalen geometrischen Muster nicht. Daher ist die Entwicklung von Methoden des maschinellen Lernens, die die Einschränkungen spezifischer geometrischer Muster präzise einbetten können, der Schlüssel, um den Engpass bekannter Materialien zu überwinden und neue Quantenphänomene zu erforschen.
Beachten Sie die Schwierigkeiten bei der Erforschung und Entwicklung von Quantenmaterialien,Das Team von Professor Mingda Li am MIT hat in Zusammenarbeit mit der Michigan State University, dem Oak Ridge National Laboratory und anderen eine Methode zur Integration geometrischer Strukturbeschränkungen namens SCIGEN (Structural Constraint Integration in a GENerative model) vorgeschlagen.Diese Methode kann an jedes vortrainierte generative Diffusionsmodell angepasst werden, um Symmetrie- und geometrische Musterbeschränkungen zu berücksichtigen und so Zielmaterialien mit spezifischen Beschränkungen zu generieren. Ein wesentlicher Vorteil dieser Methode besteht darin, dass das zugrunde liegende Modell nicht neu trainiert oder optimiert werden muss. Dies erhöht die Flexibilität und Vielseitigkeit des Frameworks erheblich und ermöglicht eine schnelle Anpassung an verschiedene vortrainierte Diffusionsmodelle, was Effizienz und Geschwindigkeit verbessert.
Die entsprechende Forschung wurde in der Top-Zeitschrift Nature Materials unter dem Titel „Structural constraint integration in a generative model for the discovery of quantum materials“ veröffentlicht.
Forschungshighlights:
* Die Studie schlägt eine Lösung vor, mit der jedes vortrainierte generative Diffusionsmodell angepasst werden kann, ohne dass das Basismodell neu trainiert oder feinabgestimmt werden muss. Dadurch wird die Abhängigkeit des traditionellen generativen Constraint-Modells von einem sekundären Training des Basismodells aufgehoben.
* Die vom Institut vorgeschlagene Methode hat den Paradigmenwechsel bei der Entdeckung von Quantenmaterialien von „Versuch und Irrtum“ zur „gerichteten Erzeugung“ gefördert und so die Entwicklung von Quantenmaterialien beschleunigt.
* Die Studie synthetisierte und charakterisierte zwei vorhergesagte Materialien, TiPd₀.₂₂Bi₀.₈₈ und Ti₀.₅Pd₁.₅Sb, die Paramagnetismus bzw. Diamagnetismus aufweisen

Papieradresse:
https://www.nature.com/articles/s41563-025-02355-y
Folgen Sie dem öffentlichen Konto und antworten Sie auf „SCIGEN Vollständiges PDF herunterladen
Weitere Artikel zu den Grenzen der KI:
Datenunterstützung: Aufbau und Screening einer umfangreichen archimedischen Gittermaterialdatenbank
In dieser Studie verwendeten Forscher SCIGEN, um eine umfassende Datenbank mit AL-Materialien (Archimedische Gitter) für die experimentelle Erforschung zusammenzustellen.
Der Datensatz enthält insgesamt 10,06 Millionen Materialien mit ALs.Nach einem vierstufigen Stabilitäts-Vorscreening blieben den Forschern über 1,01 Millionen Materialien erhalten. Anschließend führten sie Hochdurchsatz-DFT-(Dichtefunktionaltheorie)-Strukturrelaxationsberechnungen an 26.000 hochprioritären Materialien durch und konnten 24.743 Materialien erfolgreich konvergieren. Über 951 TP3T-Strukturen konvergierten, und über 531 TP3T-Materialien erreichten innerhalb von 150 Schritten der Strukturoptimierung Energieminima.
Um die magnetische Struktur zu identifizieren, verwendeten die Forscher dann ein auf einem Graph-Neuralnetzwerk basierendes Klassifizierungsmodell, wobei die DFT-optimierte Struktur von 41% als magnetisch identifiziert wurde.
Abschließend, nach der Sichtung der Materialdaten,Die Forscher synthetisierten außerdem zwei neue Materialien: TiPd₀.₂₂Bi₀.₈₈ und Ti₀.₅Pd₁.₅Sb.
Modellanalyse: Perfektionieren Sie die Designlogik und verbessern Sie die Modellfunktionen zur Materialgenerierung
SCIGEN integriert geometrische Beschränkungen direkt in den Diffusionsgenerierungsprozess und ermöglicht so Materialgenerierungsmodellen die effizientere Untersuchung stabiler Quantenmaterialien mit Zielgeometrie und Quanteneigenschaften. Mithilfe einer logischen Kette aus „Beschränkungsführung, Maskeniteration und Rauschunterdrückung“ werden ausgehend von der Zielbeschränkung zufällige Strukturen über mehrere Zeitschritte verteilt. Vor jeder Diffusion maskiert die beschränkte Struktur die entrauschte Struktur und bildet so eine induktive Vorspannung, die den Generierungsprozess auf die Erzeugung eines Ergebnisses ausrichtet, das die Beschränkungen erfüllt. Durch die iterative Anwendung der Maskierung in jedem Rauschunterdrückungsschritt werden alle zur Maske gehörenden Atome deterministisch an Positionen über alle vorgegebenen geometrischen Strukturen hinweg konvergiert. So stellt SCIGEN sicher, dass die generierten Materialien die voreingestellten geometrischen Beschränkungen erfüllen und gleichzeitig die generative Validität des zugrunde liegenden Modells erhalten bleibt.
Konkret besteht das Ziel der Kristallstrukturerzeugung darin, einen periodischen Kristall M zu finden, der aus drei Komponenten bestehen kann,Dabei handelt es sich um: eine Gittermatrix L = [l₁, l₂, l₃] ∈ R³ᕽ³ mit drei Basisvektoren, die die gesamte räumliche Struktur des Kristalls beschreiben; fraktionale Koordinaten F = [f₁, f₂, …, f៷] ∈ [0, 1)³ᕽᴺ, die die relativen Positionen der Atome im Gitter darstellen (begrenzt auf den Bereich [0, 1), um die Periodizität widerzuspiegeln); und eine One-Hot-Atomtypkodierung A = [a₁, a₂, …, a៷] ∈ [0, 1)ʰᕽᴺ, die einen Binärcode verwendet, um den spezifischen Typ jedes Atoms zu identifizieren. Während der diffusionsbasierten Materialgenerierung wendet SCIGEN geometrische Beschränkungen auf L, F und A an, um sicherzustellen, dass die generierte Struktur der Zielmorphologie entspricht.
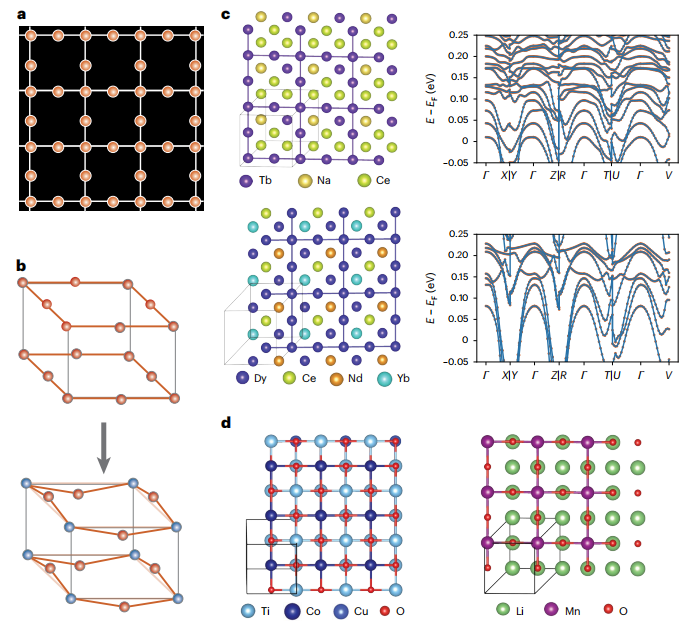
Wie in Abbildung a unten gezeigt,Zu den repräsentativen Gittern, die SCIGEN einschränken kann, gehören Dreiecksgitter, Wabengitter und Kagome-Gitter.Dies sind die Kernstrukturen, die einzigartige Quantenphänomene wie Quantenspinflüssigkeiten beherbergen.
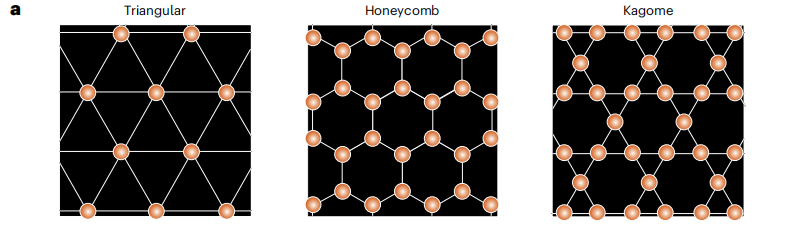
Abbildung b unten veranschaulicht den Initialisierungsprozess einer eingeschränkten Struktur. Die Grundregeln für die Initialisierung eingeschränkter Strukturen basieren auf einem „archimedischen Gitter aus magnetischen Atomen“, wodurch sichergestellt wird, dass die eingeschränkte Struktur von Anfang an potenzielle Quanteneigenschaften besitzt. Abbildung c veranschaulicht den Generierungsalgorithmus für integrierte Einschränkungskomponenten und stellt den vollständigen Prozess der „Diffusion eingeschränkter Strukturen – Initialisierung uneingeschränkter Strukturen – Fusion der beiden – iterative Rauschunterdrückung“ visuell dar.
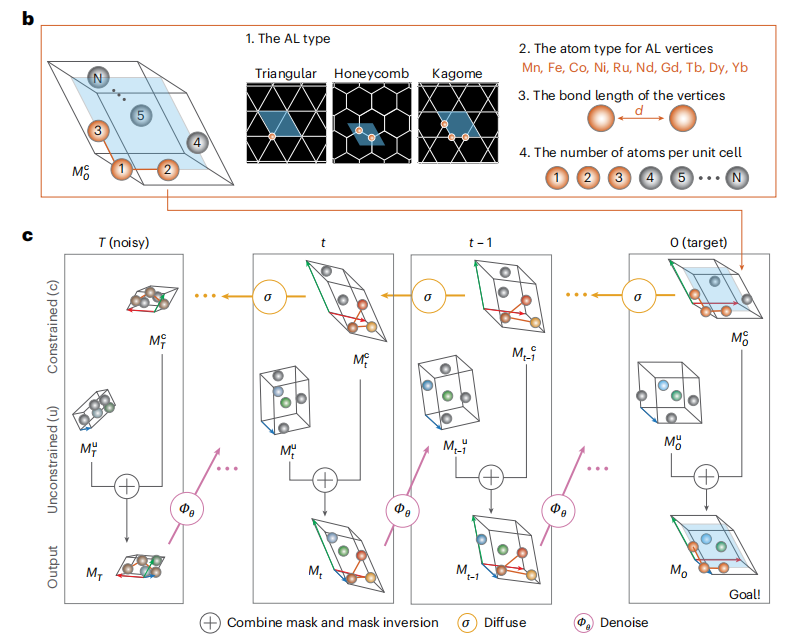
Der Kern von SCIGEN von der Initialisierung bis zur Generierung der endgültigen Struktur M₀ ist die „iterative Integration eingeschränkter und uneingeschränkter Komponenten“.Zunächst wird die initialisierte Beschränkungsstruktur (wie AL, das aus magnetischen Atomen besteht) für T=1000 Schritte einer Rauschaddition unterzogen, um bei jedem Zeitschritt die Beschränkungsstruktur Mᶜₜ (t∈[1, T]) zu erhalten.Dieser Schritt bietet einen „voreingestellten Pfad“ zur Rauschunterdrückung der eingeschränkten Komponenten und verhindert, dass die nachfolgende Generierung von der Zielgeometrie abweicht. Die uneingeschränkte Struktur besteht zunächst aus einem vollständig verrauschten Mᵘₜ, das den Teil des Generierungsprozesses darstellt, der frei optimiert werden kann. Diese beiden Strukturen werden dann integriert, um die zusammengesetzte Struktur MT zu bilden, die anschließend zu Mᵘₜ₋₁ entrauscht wird. Diese Logik wird in allen nachfolgenden Schritten wiederholt und führt schließlich einige Atome durch Iteration zur Bildung der planaren AL-Struktur, was zur Zielkristallstruktur M₀ führt.
Um die Wirksamkeit der SCIGEN-Einschränkungen zu beweisen,Die Studie hat außerdem sowohl durch mathematische Beweise als auch durch rechnerische Überprüfung bewiesen, dass SCIGEN bei der Auferlegung von Einschränkungen die ursprüngliche Verteilung des zugrunde liegenden Modells nicht zerstört.Nach der Erzeugung einer großen Anzahl von Materialien wird die Stabilität durch ein „vierstufiges Vorscreening + Hochdurchsatz-DFT-Relaxation“ bewertet, um sicherzustellen, dass potenziell stabile Kandidaten für Quantenmaterialien ausgesiebt werden.
* Ein vierstufiger Vorabprüfungsprozess kombiniert chemische Regeln, die die Ladungsneutralität und das von Atomen eingenommene Volumen der Elementarzelle prüfen, mit einem zusätzlichen neuronalen Netzwerk, das die Stabilität basierend auf dem Eₕᵤₗₗ-Wert der konvexen Hüllenenergie vorhersagt (je niedriger der Eₕᵤₗₗ-Wert, desto thermodynamisch stabiler ist das Material).
* Mittels Hochdurchsatz-DFT-Relaxation werden Dichtefunktionaltheorie-Berechnungen an den untersuchten Materialien durchgeführt. Durch Strukturrelaxation (Optimierung der Atompositionen und Elementarzellenabmessungen) identifizieren wir schließlich Kandidaten mit potenzieller Stabilität und schaffen so die Grundlage für die anschließende experimentelle Synthese oder eingehende Forschung.
Experimentelle Verifizierung: SCIGEN demonstriert herausragende Fähigkeiten zur Richtungserzeugung und Materialvorhersage
Im konkreten Experiment übernahm das Basismodell das DiffCSP-Modell, wodurch auch die Beibehaltung der Fähigkeiten des Basisgenerationsmodells bestätigt wurde.
Erste,Die Experimente zeigen die Ergebnisse der Materialerzeugung unter drei Haupteinschränkungen der AL:Die Fähigkeit von SCIGEN zur gerichteten Generierung wird anhand des Dreiecksgitters, des Wabengitters und des Kagome-Gitters überprüft, wie in der folgenden Abbildung dargestellt.
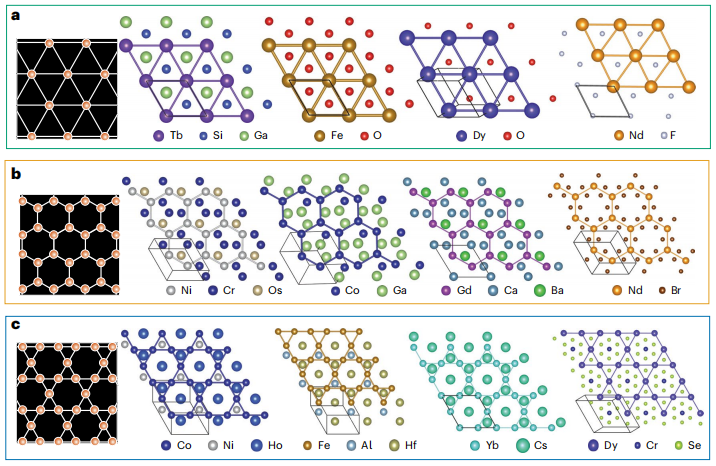
Die Ergebnisse zeigen, dassSCIGEN kann eingeschränkte Atome präzise dazu anleiten, sich in vordefinierten geometrischen Mustern anzuordnen, und die Einschränkungen wirken nur auf die Zielkomponenten.Die Positionen der freien Atome sind nicht streng definiert, wodurch ein gerichteter und flexibler Entstehungsprozess gewährleistet wird. Die Positionen der freien Atome werden während des Entstehungsprozesses auf natürliche Weise bestimmt und von räumlichen und bindungsbedingten Faktoren beeinflusst. Bei Dreiecksgittern neigen freie Atome dazu, Positionen einzunehmen, die drei magnetische Atome verbinden und so gleichseitige Dreiecke bilden. Bei Wabengittern erscheinen freie Atome typischerweise im Zentrum von Sechsecken, die aus magnetischen Atomen gebildet werden, koplanar mit den Gitterebenen. Bei Kagome-Gittern verbinden freie Atome die gleichseitigen Dreiecke und Sechsecke jeder Kagome-Gitterschicht. Wenn der Innenraum des Gitterpolygons zu eng ist, werden sie außerhalb der AL-Ebene versetzt. Bei größeren Polygonen, wie Sechsecken, können sie koplanar mit den freien Atomen angeordnet werden.
Um begrenzte Materialstrukturen mit einer höheren Stabilitätswahrscheinlichkeit zu erzeugen, entwickelten die Forscher außerdem ein Stichprobenschema für die Anfangsbedingungen, indem sie die Überlebensraten der Vorprüfung analysierten. Der Schlüssel liegt in der Bestimmung der optimalen Wahl der „Anzahl der Atome pro Elementarzelle (N)“ und der „Art der magnetischen Atome an den AL-Scheitelpunkten“. Die Forscher wählten zunächst N Werte aus einer gleichmäßigen Verteilung aus und berechneten die entsprechenden „mehrstufigen Überlebensraten der Vorprüfung“ für verschiedene N Werte, um eine stabile Wahrscheinlichkeitsverteilung für N zu erhalten. Basierend auf dieser Verteilung wurde dann N abgetastet, um die Generierung im großen Maßstab zu initialisieren: Dreiecksgitter eignen sich besser für kleinere N Werte, während Waben- und Kagome-Gitter besser für größere N Werte geeignet sind. Dies ist in Abbildung d unten dargestellt.
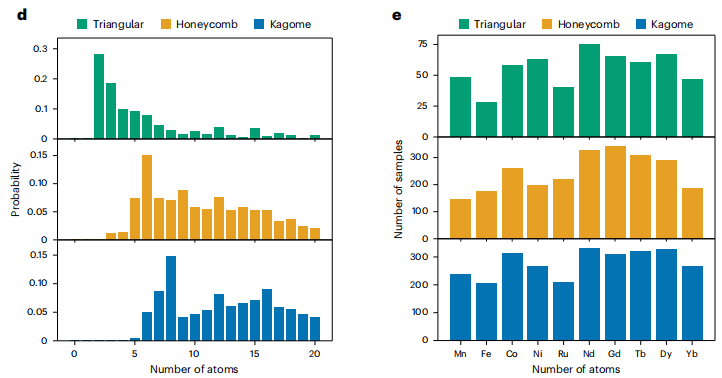
Abbildung e: Die Menge des Materials, die nach der Vorabprüfung auf gängige magnetische Atomtypen in jedem größeren geometrischen Muster übrig bleibt.
Wie in Abbildung e oben gezeigt, wurden 10 gängige magnetische Atome (Mn, Fe, Co, Ni, Ru, Nd, Gd, Tb, Dy, Yb) experimentell getestet.Für jeden Gittertyp und jedes magnetische Atom wurden 3.000 Materialien erzeugt und die Anzahl der stabilen Materialien nach der Vorprüfung gezählt.Die Ergebnisse zeigen, dass, obwohl die Menge an stabilen Materialien für verschiedene magnetische Atome variiert, alle zehn Arten magnetischer Atome AL-Strukturen bilden können. Daher wird bei der Erzeugung in großem Maßstab für die AL-Vertex-Atomtypen eine „Equal Probability Sampling“-Methode verwendet, um sowohl Diversität als auch Stabilität zu berücksichtigen.
Zusätzlich zu den drei oben genannten Hauptgittern kann SCIGEN auch auf andere archimedische Gitter wie Quadrate, längliche Dreiecke und abgeschnittene Quadrate angewendet werden, sodass insgesamt sieben Arten von AL-gebundenen Materialien entstehen. Unbeschränkte Atome spielen in diesen Gittern ebenfalls eine Schlüsselrolle, indem sie die Lücken zwischen den Gitterschichten überbrücken und so die mechanische und thermische Stabilität der Struktur erhöhen. Sie können sogar spontan erkennbare AL-Muster bilden, was darauf hindeutet, dass AL-Strukturen eine „feste Stabilitätspräferenz“ in lokalen Koordinaten aufweisen und so eine Grundlage für die Erforschung einzigartigerer Quantenmaterialien bilden. (Siehe Abbildung unten.)

Als Variation des quadratischen AL,Die Forscher demonstrierten außerdem experimentell den Durchbruch von SCIGEN bei der Erzeugung von Lieb-Gittermaterialien.Die Ergebnisse zeigen, dass SCIGEN durch geometrische Einschränkungen stabile Lieb-ähnliche Gittermaterialien erzeugen kann, was seine Fähigkeit zur Erzeugung seltener Gitterstrukturen bestätigt. In diesen Lieb-ähnlichen Materialien sind magnetische Atome wie Tb und Dy an den Knotenpunkten des Lieb-Gitters ausgerichtet, was die Grundlage für Untersuchungen magnetischer Eigenschaften bildet. Anschließende DFT-Strukturrelaxationsrechnungen der erzeugten Materialien zeigten, dass die gesamte Lieb-Gitterarchitektur intakt bleibt. Weitere Bandberechnungen ergaben, dass diese Materialien die erwarteten elektronischen Flachbandeigenschaften nahe dem Fermi-Niveau aufweisen. Dies bestätigt, dass die mit SCIGEN erzeugten Materialien nicht nur strukturell stabil sind, sondern auch das einzigartige quantenelektronische Verhalten des Lieb-Gitters aufweisen. Dies ist in der folgenden Abbildung dargestellt.
Um Lieb-ähnliche Gittermaterialien in Richtung oxidischer Analoga praktischer supraleitender Materialien zu entwickeln, hat SCIGEN eine Strategie der „adaptiven Demaskierung“ eingeführt, die ein Gleichgewicht zwischen Zwangsstarrheit und struktureller Flexibilität herstellt und so eine Brücke zwischen der Grundlagenforschung zu Lieb-Gittern und der Erforschung supraleitender Anwendungen schlägt.
Um die Vorhersagefähigkeit und Wirksamkeit von SCIGEN zu überprüfen,Die Forscher synthetisierten und testeten zwei völlig neue Verbindungen – TiPd₀.₂₂Bi₀.₈₈ und Ti₀.₅Pd₁.₅Sb.Experimente zeigen, dass die experimentellen Ergebnisse trotz geringfügiger Unterschiede in der Stöchiometrie und Kristallsymmetrie zu den von SCIGEN vorhergesagten Gegenstücken dennoch weitgehend mit den berechneten Ergebnissen übereinstimmen. Erstere weisen Paramagnetismus auf, letztere Diamagnetismus.Dies zeigt die Fähigkeit von SCIGEN, chemisch plausible Strukturmotive vorzuschlagen, die, obwohl nicht in idealisierter Form, dennoch eine Grundlage und einen Wert für weitere Untersuchungen bieten können.
Zusammenfassend lässt sich sagen, dass SCIGEN als innovatives allgemeines Framework auf Basis maschinellen Lernens bisher unzugängliche Bereiche im Bereich der Materialentwicklung erschließt und den Weg für Durchbrüche bei Quantenmaterialien auf der Grundlage der Beziehung zwischen Struktur und Leistung ebnet.
Quantenmaterialentdeckung und künstliche Intelligenz prallen aufeinander und erzeugen ein brillantes Feuerwerk
Die „Struktur-Leistungs-Beziehung“ ist zu einem zentralen Konzept in der aktuellen Forschung und Entwicklung neuer Materialien geworden. Sie bietet zwei wesentliche Vorteile: Erstens ermöglicht sie das Verständnis der funktionalen Quantenphänomene von Materialien durch ihre Struktur; zweitens ermöglicht sie die Vorhersage der Mikrostruktur des Materials durch ihre Leistung und drittens ermöglicht sie durch Strukturmanipulation die gezielte Gestaltung von Zielmaterialien. Die Entwicklung künstlicher Intelligenz eröffnet Wissenschaftlern zweifellos neue Möglichkeiten, die Beziehung zwischen diesen beiden Aspekten systematisch zu untersuchen und so die Forschung und Entwicklung neuer Materialien zu beschleunigen.
Zusätzlich zu den oben genannten Errungenschaften verfügt die wissenschaftliche Forschungsgemeinschaft über eine lange Geschichte der Untersuchung der Struktur-Leistungs-Beziehung, wie beispielsweise die Forschung zum im Artikel erwähnten Basismodell.Unter anderem veröffentlichte das Google DeepMind-Team eine Studie mit dem Titel „Scaling deep learning for materials discovery“.Um eine maschinelle Lernerweiterung der Materialerkundung durch aktives Lernen im großen Maßstab zu erreichen, wird eine Methode namens GNoME (Graph Networks for Materials Exploration) vorgeschlagen.
Die Methode basiert auf zwei Schlüsselkomponenten: Erstens der Etablierung von Methoden zur Generierung diverser Kandidatenstrukturen, wie beispielsweise der symmetriebewussten partiellen Substitution (SAPS) und der Zufallsstruktursuche; und zweitens der Verwendung fortschrittlicher Graph-Neural-Networks (GNNs) zur Vorhersage der Gesamtkristallenergie. In einem iterativen Prozess nutzt das GNoME-Modell vorhandene Daten, um Kandidatenstrukturen zu trainieren und zu screenen. DFT-Energieberechnungen verifizieren die Vorhersagen und liefern Daten für die nächste Trainingsrunde. Letztendlich wurden über 2,2 Millionen stabile Strukturen entdeckt.Die aktualisierte konvexe Hülle enthält 381.000 neue Einträge.Die Anzahl stabiler Kristalle hat sich im Vergleich zu früher um eine Größenordnung erhöht.
Papieradresse:
https://www.nature.com/articles/s41586-023-06735-9
Das den oben genannten Experimenten zugrunde liegende Modell stammt aus einer Studie mit dem Titel „Crystal Structure Prediction by Joint Equivariante Diffusion“, die von Teams der Tsinghua-Universität, der Renmin-Universität China und der Sun Yat-sen-Universität durchgeführt wurde.In der Studie wurde eine Methode namens DiffCSP vorgeschlagen, um das schwierige Problem der Kristallstrukturvorhersage zu lösen.Das Modell basiert auf einem periodischen äquivarianten Rauschunterdrückungsmodell und generiert gemeinsam die Gitter- und Atomkoordinaten jedes Kristalls, wodurch die Kristallgeometrie besser modelliert werden kann.
Papieradresse:
https://arxiv.org/abs/2309.04475
Zusammenfassend lässt sich sagen, dass die SCIGEN-Methode eine Innovation darstellt, die auf früheren Erkenntnissen basiert. Sie verfeinert das grundlegende Diffusionsmodell durch „eingeschränkte Integration“, eröffnet einen neuen, zielgerichteten und effizienten Weg zur Entdeckung von Quantenmaterialien und fördert die Forschung und Entwicklung von Quantenmaterialien vom „skalierten Ausprobieren“ zum „gerichteten Design“. Ihre Vielseitigkeit legt zudem den Grundstein für die anschließende Erforschung von Materialien mit unbekannten Quantenstrukturen und -eigenschaften.