Sigmoid 函数 Sigmoid Function
Sigmoid 函数是常见的 S 型函数，也被称为 S 型生长曲线，由于其具有单增、反函数单增等性质，Sigmoid 函数常被用作神经网络的阈值函数，将变量映射到 0,1 之间。
Sigmoid 函数基本性质
Sigmoid 函数形式与图像如下：
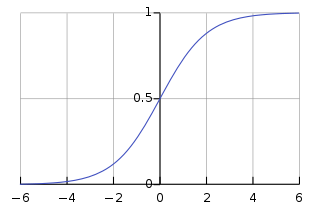
- 定义域：( −∞ , +∞ )；
- 值域：(− 1 , 1 )；
- 函数在定义域内为连续光滑函数；
- 处处可导，导数为：f′ ( x ) = f ( x ) ( 1 − f ( x ) )；
- 函数的取值在 0 到 1 之间，在 0.5 处呈中心对称，且越靠近 x = 0 的取值斜率越大。
Sigmoid 函数与逻辑回归
根据逻辑回归 LR 的目的，选择函数时必须满足以下两个条件：
1）取值范围在 0~1 之间；
2）对于一个事件发生情况， 50% 是结果的分水岭，选择函数应该在 0.5 中心对称。
基于这两点， Sigmoid 正好符合 LR 的需求。