总结

华为诺亚方舟实验室的研究人员推出了 ROOT，这是一种用于大型语言模型的鲁棒正交化优化器，通过采用自适应牛顿迭代和近端优化来克服现有动量正交化方法的维度脆弱性和噪声敏感性，从而增强训练稳定性和收敛速度。

简介

预训练大型语言模型 (LLM) 不断增长的计算需求要求优化器在大规模下既高效又稳定。虽然像 AdamW 这样的标准方法和像 Muon 这样较新的矩阵感知方法推动了该领域的发展，但它们往往面临数值不稳定性和精度差距的问题。具体而言，现有的基于正交化的优化器依赖于无法适应变化矩阵维度的固定系数近似，并且仍然对可能破坏更新方向的离群数据样本产生的梯度噪声敏感。

作者介绍了 ROOT（鲁棒正交化优化器），这是一个旨在增强针对结构不确定性和数据级噪声鲁棒性的新颖框架。通过改进权重矩阵的正交化方式和梯度的过滤方式，ROOT 确保了大规模神经网络的可靠训练，且不牺牲计算效率。

关键创新包括：

• 自适应正交化： 该方法采用具有特定维度系数的 Newton-Schulz 迭代，以确保跨不同网络架构的高精度，取代了不精确的固定系数方案。
• 噪声抑制： 近端优化项利用软阈值处理来主动减轻由离群值引起的梯度噪声的破坏性影响。
• 增强收敛性： 与当前最先进的优化器相比，该方法实现了更快的训练速度，并在嘈杂、非凸场景中表现出更优越的性能。

方法

作者利用一个框架，通过解决现有方法中的两个关键限制——对矩阵维度的敏感性和对离群值引起的梯度噪声的脆弱性，来增强基于正交化优化的鲁棒性。整体方法集成了用于 Newton-Schulz 迭代的自适应系数学习和通过软阈值进行的离群值抑制，形成了一个统一的优化过程。

该方法的核心是 Newton-Schulz (NS) 迭代，它通过迭代细化初始矩阵 $X_0 = M_t / \|M_t\|_F$X0​=Mt​/∥Mt​∥F​ 来近似正交变换 $(M_t M_t^T)^{-1/2} M_t$(Mt​MtT​)−1/2Mt​。每次迭代 $k$k 的更新规则定义为：

$$X_k = a X_{k-1} + b X_{k-1} (X_{k-1}^T X_{k-1}) + c X_{k-1} (X_{k-1}^T X_{k-1})^2$$Xk​=aXk−1​+bXk−1​(Xk−1T​Xk−1​)+cXk−1​(Xk−1T​Xk−1​)2

这种递归通过多项式映射 $g(x) = a x + b x^3 + c x^5$g(x)=ax+bx3+cx5 作用于输入矩阵的奇异值，经过 $T$T 次迭代后，得到的矩阵 $X_T$XT​ 近似于正交化动量。标准的 Muon 优化器采用固定系数 $a = 3.4445$a=3.4445、$b = -4.7750$b=−4.7750 和 $c = 2.0315$c=2.0315，这些系数针对平均矩阵形状进行了优化，但在具有不同维度的矩阵上表现不佳。

为了克服这种维度脆弱性，作者引入了自适应 Newton-Schulz 迭代 (AdaNewton)，其中系数 $a^{(m,n)}$a(m,n)、$b^{(m,n)}$b(m,n) 和 $c^{(m,n)}$c(m,n) 是专门为网络中每个矩阵大小 $(m, n)$(m,n) 学习的。这种细粒度的适应性确保了不同维度层之间一致的正交化质量。自适应更新规则如下：

$$X_k = a^{(m,n)} X_{k-1} + b^{(m,n)} X_{k-1} (X_{k-1}^T X_{k-1}) + c^{(m,n)} X_{k-1} (X_{k-1}^T X_{k-1})^2$$Xk​=a(m,n)Xk−1​+b(m,n)Xk−1​(Xk−1T​Xk−1​)+c(m,n)Xk−1​(Xk−1T​Xk−1​)2

这些系数在训练期间与模型参数联合优化，允许正交化过程适应每一层的谱属性。这种方法从“一刀切”的策略转变为维度鲁棒的设计，确保了整个网络中稳定可靠的梯度更新。

[[IMG:|ROOT 优化器的框架图]]

框架图展示了自适应正交化和离群值抑制的集成。动量矩阵 $M_t$Mt​ 首先使用软阈值分解为基础分量 $B_t$Bt​ 和离群分量 $O_t$Ot​。离群分量被丢弃，而基础分量通过 AdaNewton 进行鲁棒正交化。生成的正交化矩阵随后用于更新模型参数。

为了进一步增强鲁棒性，该方法结合了软阈值处理以抑制梯度离群值。动量矩阵 $M_t$Mt​ 被建模为基础分量 $B_t$Bt​ 和离群分量 $O_t$Ot​ 的和，鲁棒分解被公式化为一个惩罚大幅值元素的凸优化问题。该问题的解由软阈值算子给出：

$$\mathcal{T}_{\varepsilon}[x]_i = \operatorname{sign}(x_i) \cdot \max(|x_i| - \varepsilon, 0)$$Tε​[x]i​=sign(xi​)⋅max(∣xi​∣−ε,0)

此操作平滑地收缩超过阈值 $\varepsilon$ε 的梯度值，在保留幅值相对顺序的同时抑制极端值。该分解逐元素应用于动量矩阵，得到：

$$O_t = \mathcal{T}_{\varepsilon}(M_t), \quad B_t = M_t - O_t$$Ot​=Tε​(Mt​),Bt​=Mt​−Ot​

通过仅对截断后的基础分量 $B_t$Bt​ 应用正交化，该方法确保敏感的 NS 迭代在稳定的梯度上运行，减轻了离群噪声的放大。这种设计提供了一种连续、可微的硬截断替代方案，在保持梯度方向的同时提高了训练稳定性。完整的优化过程总结在 ROOT 优化器算法中，该算法在一个迭代循环中结合了动量累积、离群值抑制和自适应正交化。

实验

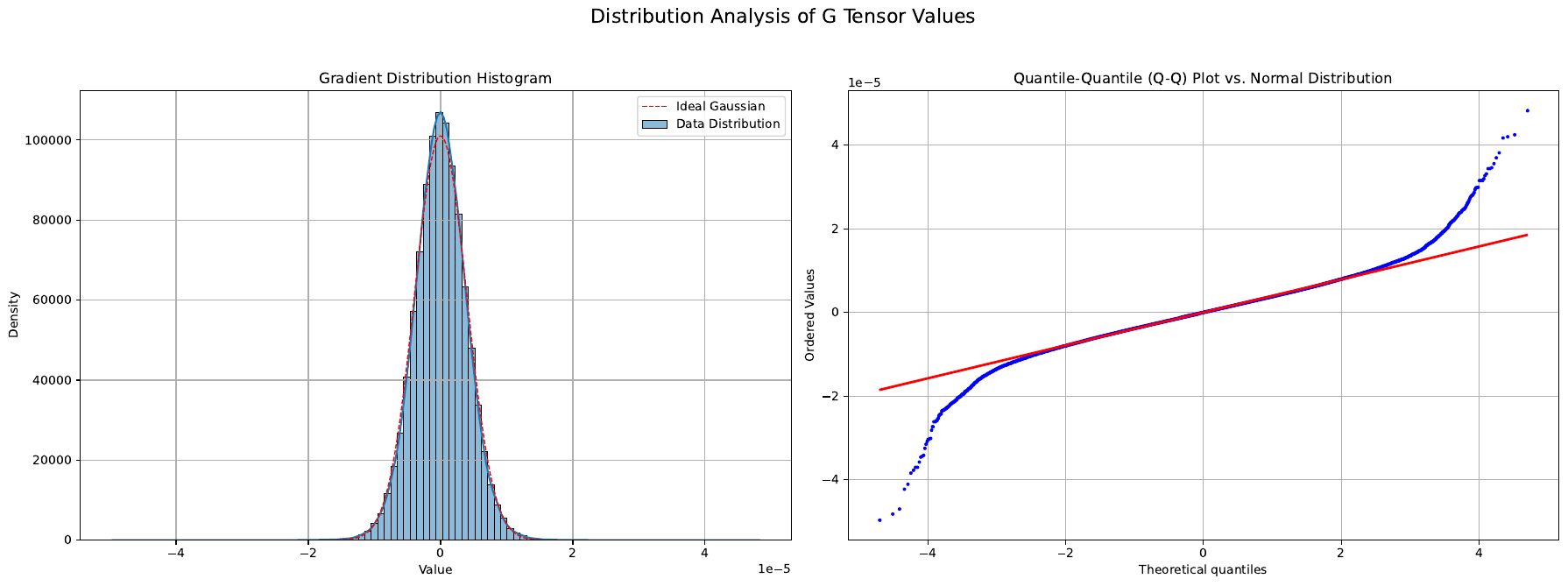
• 梯度动力学验证： 使用前 1 万个预训练步骤的梯度比较了正交化策略；ROOT 保持了比 Muon 和经典 Newton-Schulz 更低的相对误差，证实了维度感知系数能更好地近似真实 SVD。
• LLM 预训练： 在 FineWeb-Edu 子集（100 亿和 1000 亿 token）上训练了一个 1B Transformer；ROOT 实现了 2.5407 的最终训练损失，超过 Muon 基线 0.01。
• 学术基准： 评估了 HellaSwag 和 PIQA 等任务的零样本性能；ROOT 取得了 60.12 的平均分，优于 Muon (59.59) 和 AdamW (59.05)。
• 消融研究： 确定了 0.90 百分位阈值是离群值抑制的最佳选择，并选择了混合 (1:3) 校准策略以确保稳定性同时防止过拟合。
• 视觉泛化： 在 CIFAR-10 上训练了一个 Vision Transformer；ROOT 始终获得比 Muon 基线更高的准确率，验证了该方法在非语言模态上的有效性。

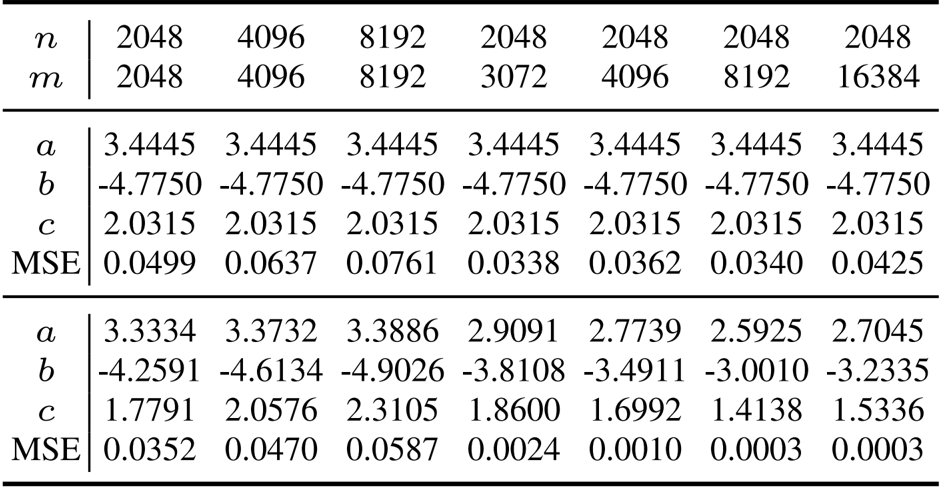
作者使用提供的表格证明，与固定系数方法相比，ROOT 优化器的形状特定系数在各种矩阵维度上实现了更低的均方误差 (MSE)。结果表明，随着系数值适应不同的矩阵形状，MSE 显著降低，表明在训练期间对不同层几何形状的近似保真度有所提高。

作者在一系列学术基准上评估了 ROOT 优化器与 AdamW 和 Muon 的对比，结果显示 ROOT 在所有任务中都实现了更高的零样本性能。具体而言，ROOT 在 HellaSwag、PIQA、OBQA、SciQ、Wino 和 WSC 中均优于这两个基线，平均得分为 60.12，超过了 AdamW 的 59.05 和 Muon 的 59.59。

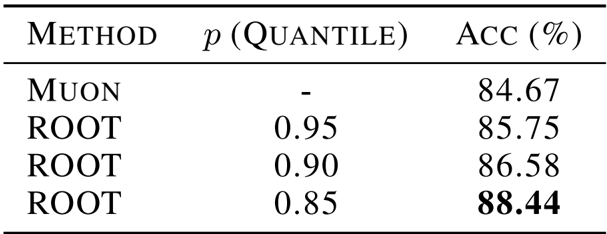
作者在 CIFAR-10 上训练的 Vision Transformer 上评估了不同百分位阈值对 ROOT 优化器中离群值抑制的影响。结果表明，阈值的选择显著影响性能，较低的 0.85 百分位产生了最高的准确率 88.44%，优于 Muon 基线和其他 ROOT 配置。这表明更积极的离群值抑制可以增强视觉任务的泛化能力。