总结

来自格勒诺布尔-阿尔卑斯大学、纽约大学和基因泰克的研究人员推出了 MIST，这是一种完全数据驱动的互信息估计器，在合成元数据集上进行训练，利用分位数回归提供校准的不确定性区间，为依赖经验泛化而非理论保证的经典基线提供了一种可微且高效的替代方案。

简介

互信息 (MI) 是数据科学中量化变量间非线性依赖关系的关键指标，是特征选择、表征学习和凯果关系等任务的基石。由于现实世界数据的真实概率分布鲜为人知，从业者依赖估计器从有限样本中推断 MI。然而，现有的技术——无论是直接估计数据密度还是近似密度比——往往在具有挑战性的现实场景中表现不佳。这些方法在处理高维数据、有限样本量或复杂分布时往往会失效，而且它们通常仅在掩盖了这些性能差距的简单、低 MI 高斯基准上进行验证。

为了克服这些限制，作者推出了 MIST（通过监督训练进行互信息估计），这是一个将 MI 估计重新构建为监督学习问题而非数学推导的框架。作者没有在推理过程中近似密度函数，而是使用具有已知真实 MI 值的大规模合成分布元数据集端到端地训练神经网络。这使得模型能够直接学习从数据样本到信息内容的映射。

该方法的关键创新和优势包括：

• 低数据环境下的鲁棒性： 该估计器在困难设置中显著优于现有基线，即使在样本量少至 10 到 500 个以及更高维度的情况下也能提供可靠的估计。
• 计算效率： 通过在训练期间摊销计算成本，该模型执行推理的速度比先前的神经方法快几个数量级，仅需单次前向传播。
• 校准的不确定性： 该架构结合了分位数回归以提供内置的、经过良好校准的置信区间，提供了标准点估计方法所缺乏的可靠性。

数据集

作者使用 BMI 库构建了一个合成元数据集，以实现对具有已知互信息 (MI) 的分布进行监督学习。数据集组织如下：

• 数据集构成与来源 元数据集由通过对基础族应用可逆变换生成的合成分布组成，这些基础族具有解析 MI。每个条目或“元样本”将来自特定分布的联合样本与其真实 MI 值配对。

• 分布类别 数据根据其与训练数据的关系分为两大类：

  • 元分布内 (IMD)： 此子集包括基础分布，如多元正态分布（具有密集或潜变量模型变体）和多元学生 $t$t 分布（具有密集或稀疏结构）。这些族共享协方差结构，但在尾部厚度和参数化方面有所不同。
  • 元分布外 (OoMD)： 此子集包含训练集中完全不存在的分布族，用于测试泛化能力。它具有多元加性噪声模型，其特征是非高斯属性和有界支持，其中噪声由共享的尺度参数控制。

• 数据划分与使用 为了促进多样性，作者将分布族划分为不相交的训练组和测试组。为了评估，他们构建了两个不同的语料库：

  • 标准基准： 一个较小的测试集，旨在与现有的计算密集型估计器进行比较。
  • 扩展基准： 一个较大的测试集，用于评估对新颖分布和更高维度的泛化能力。

• 处理与元数据

  • 维度： 数据集中的样本维度从 2 到 32 不等。
  • 真实值： 真实的 MI 值根据特定分布族的可处理性，通过解析或数值方法计算得出。
  • 参数采样： 结构超参数（如相关性、潜在信号强度和自由度）从特定的均匀分布中采样，以确保每个族内的多样性。

方法

作者提出了一个完全数据驱动的互信息估计框架，将该问题重新构想为一个监督学习任务，即模型学习从有限样本中直接预测互信息。这种方法被称为 MIST（通过监督训练进行互信息估计），它通过训练神经网络将一组配对样本 $\{(x_i, y_i)\}_{i=1}^n${(xi​,yi​)}i=1n​ 映射到 $I(X;Y)$I(X;Y) 的估计值，从而绕过了传统的密度估计或比率近似方法。该模型在大型合成联合分布元数据集上进行端到端训练，其中每个训练示例由样本数据集及其对应的真实互信息值组成。学习目标是最小化预测 MI 与真实 MI 之间的均方误差，有效地训练模型以逼近贝叶斯最优回归函数，该函数输出给定观测数据的 MI 后验期望。

如下图所示，该框架由两个主要部分组成：合成元数据集和监督预测模型。元数据集是通过从多样化的联合分布族中采样构建的，每个分布都有已知的互信息值，并生成不同大小和维度的有限数据集。预测模型 MIST 旨在处理这些大小可变的数据集，同时对样本顺序保持不变。模型架构基于 SetTransformer++ 框架，非常适合处理无序数据集。该架构的核心是一系列 ISAB（集合内注意力块）层，它们对固定数量的学习诱导点执行注意力机制，从而能够高效处理可变长度的输入。为了处理可变输入维度，引入了一个额外的行宽注意力块，它沿特征轴操作并使用学习到的池化机制将维度减少到固定大小。此行池化步骤确保模型可以处理不同维度的输入。处理后的特征随后通过最终的 MLP（多层感知机）以产生 MI 预测。该模型可以训练为使用均方误差损失预测 MI 的点估计，或使用弹球损失预测 MI 分布的分位数，从而实现内置的不确定性量化。该框架旨在对实践中遇到的广泛 MI 值具有鲁棒性，作者发现只要元数据集包含足够范围的 MI 标签，直接预测 MI 就能产生最佳性能。

实验

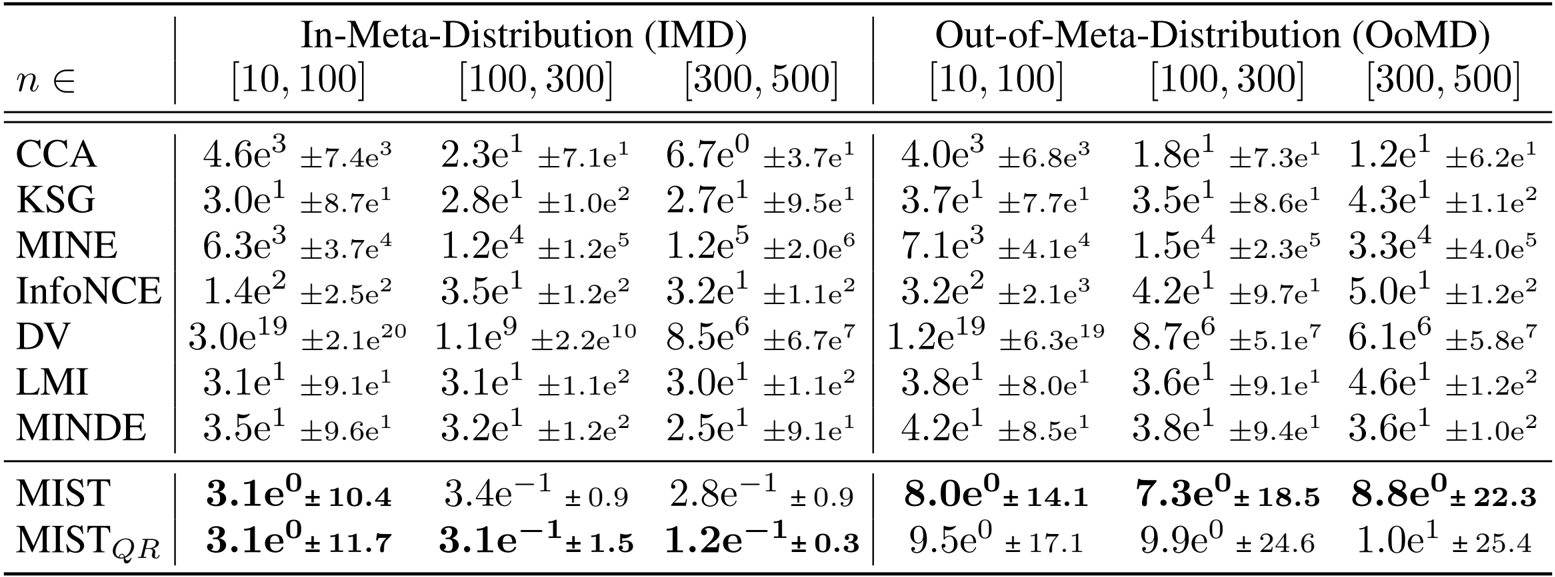
• 在合成分布上与现有方法进行的基准测试验证了学习到的估计器优于基线，在见过的分布上误差降低了约 10 倍，在未见过的分布上误差降低了 5 倍。
• 在高维和低样本环境中，模型表现出的损失比 KSG 基线低高达 100 倍，并避免了通常与估计大互信息值相关的负偏差。
• 扩展性和效率实验表明，该方法仅需最佳基线约一半的样本即可获得可靠估计，并且推理速度比 KSG 快 4 到 80 倍。
• 不确定性量化分析证实，基于分位数的区间经过良好校准，在测试设置中产生的覆盖率比 KSG 好约 2 倍。
• 泛化研究表明，在未见过的分布和样本量上表现稳健，尽管当同时遇到未见过的分布和更高维度时，准确性会下降。
• 可变维度实验表明，与专门的单维度模型相比，在混合维度上进行训练可使高维数据 ($D \ge 16$D≥16) 的均方误差降低 2 到 3 倍。

作者使用该表比较了他们学习到的估计器 MIST 和 MIST_QR 与几种现有方法在不同样本量和分布类型下的性能。结果表明，MIST 和 MIST_QR 的均方误差显著低于所有基线，特别是在低样本和高维设置中，其中 MIST_QR 在不确定性估计中表现出卓越的校准性和可靠性。