بقلم سيمونا إيفانوفا
خبير الذكاء الاصطناعي والتعلم الآلي
العمل في مجلة العلوم
مقدمة عن HyperAI
يعد الانتشار الخلفي (BP) حاليًا الطريقة الأكثر شيوعًا وفعالية لتدريب خوارزميات الشبكة العصبية الاصطناعية (ANN).
ظهرت ظاهرة الانتشار العكسي لأول مرة في سبعينيات القرن العشرين، ولكنها لم تحظ بالاهتمام من جميع مناحي الحياة إلا بعد أن نشر جيفري هينتون بحثه "تعلم التمثيلات عن طريق أخطاء الانتشار العكسي" في عام 1986.
جيفري هينتون: المخترع المشارك لخوارزمية الانتشار الخلفي
جيفري هينتون
جيفري هينتون هو عالم كمبيوتر وعالم نفس كندي من أصل بريطاني قدم العديد من المساهمات في مجال الشبكات العصبية. وهو أحد مخترعي خوارزمية الانتشار الخلفي ومروج نشط للتعلم العميق. يُعرف بأنه والد الشبكات العصبية والتعلم العميق.
بالإضافة إلى ذلك، يعد هينتون مؤسس مركز غاتسبي لعلوم الأعصاب الحاسوبية في جامعة لندن، وهو حاليًا أستاذ في قسم علوم الكمبيوتر في جامعة تورنتو، كندا. تتركز اهتماماته البحثية الرئيسية في تطبيق الشبكات العصبية الاصطناعية في التعلم الآلي والذاكرة والإدراك ومعالجة الرموز. يقوم هينتون حاليًا باستكشاف كيفية تطبيق الشبكات العصبية على خوارزميات التعلم غير الخاضعة للإشراف.
ومع ذلك، من بين العديد من نتائج البحث العلمي التي توصل إليها هينتون، فإن الانتشار الخلفي هو الأكثر شهرة ويشكل الأساس لمعظم خوارزميات الشبكات العصبية للتعلم الخاضع للإشراف الحالية، والتي تعتمد على طريقة الانحدار التدرجي. مبدأ عملها الرئيسي هو:
في التشغيل الفعلي، يتم تقسيم خوارزمية ANN بشكل عام إلى ثلاث فئات: طبقة الإدخال، والطبقة المخفية، وطبقة الإخراج. عندما يكون هناك خطأ بين نتيجة إخراج الخوارزمية ونتيجة الهدف، فإن الخوارزمية ستحسب قيمة الخطأ، ثم تقوم بإعادة قيمة الخطأ إلى الطبقة المخفية من خلال الانتشار الخلفي، وتعديلها عن طريق تعديل المعلمات ذات الصلة، وتكرر هذه الخطوة حتى يتم الحصول على النتيجة المتوقعة.
يسمح الانتشار الخلفي لخوارزمية الشبكة العصبية الاصطناعية باستخلاص نتائج أقرب إلى الهدف. ومع ذلك، قبل فهم كيفية تطبيق الانتشار الخلفي على خوارزمية الشبكة العصبية الاصطناعية، من الضروري أولاً فهم مبدأ عمل الشبكة العصبية الاصطناعية.
كيف تعمل الشبكات العصبية الاصطناعية
الشبكة العصبية الاصطناعية (ANN) هو نموذج رياضي أو نموذج حسابي يعتمد على الشبكة العصبية في الدماغ البشري، والتي تتكون من عدد كبير من العقد (والتي يمكن فهمها على أنها خلايا عصبية بيولوجية) متصلة ببعضها البعض.
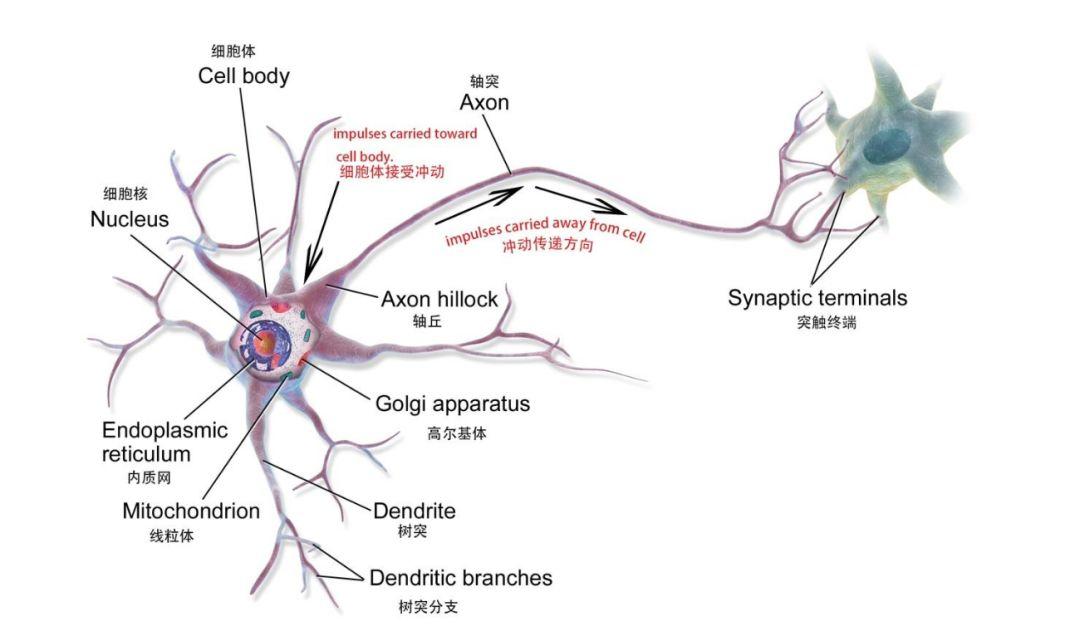
الخلايا العصبية البيولوجية
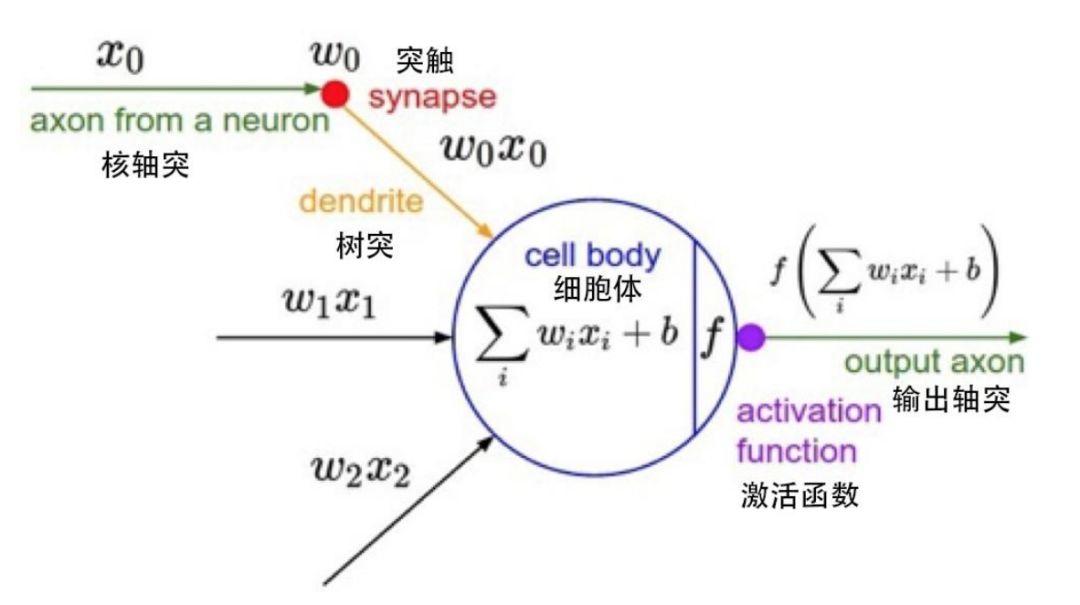
عقدة واحدة في نموذج رياضي
تمثل كل عقدة دالة إخراج محددة، تسمى دالة التنشيط؛ يمثل الاتصال بين عقدتين قيمة مرجحة، تسمى أيضًا قيمة الوزن. أثناء تشغيل خوارزمية الشبكة العصبية الاصطناعية، يتوافق كل اتصال مع الوزن w والإزاحة b (المعروفة أيضًا باسم معلمات الشبكة العصبية الاصطناعية). ترتبط قيمة الإخراج بالعقدة وقيمة الوزن والإزاحة.
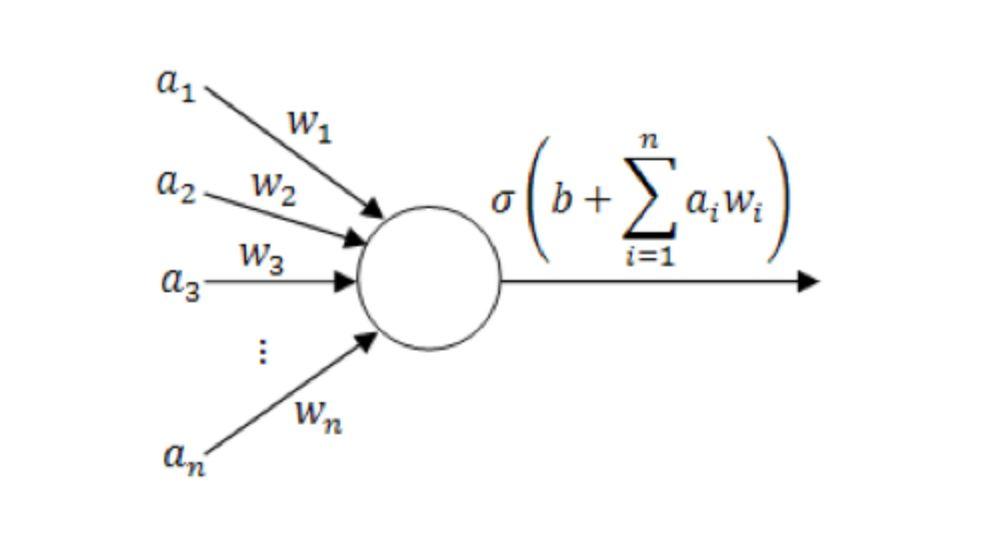
مخطط نموذج الخلية العصبية الفردية
(حيث أ1~أن هي مكونات متجه الإدخال؛ و1~ون هي قيمة الوزن؛ ب هو الإزاحة؛ σ هي دالة التنشيط، مثل tanh، Sigmoid، ReLU، إلخ.)
تتكون الشبكة العصبية الاصطناعية الكاملة عادةً من طبقة إدخال، وطبقات مخفية متعددة، وطبقة إخراج. تتكون الطبقة المخفية بشكل أساسي من الخلايا العصبية وهي التي تقوم بأهم أعمال الحوسبة. أثناء العملية الفعلية، سوف تتخذ الخلايا العصبية في كل طبقة القرارات وتنقل القرارات إلى الخلايا العصبية في الطبقة المخفية التالية حتى يتم إخراج النتيجة النهائية.
لذلك، كلما زاد عدد الطبقات المخفية، أصبحت الشبكة العصبية الاصطناعية أكثر تعقيدًا وستكون النتائج أكثر دقة. على سبيل المثال، إذا كنت تريد استخدام شبكة عصبية اصطناعية لتحديد ما إذا كان الحيوان المدخل "قطة" أو "ليس قطة"، فبعد إدخال الحيوان، ستصدر الخلايا العصبية في كل طبقة مخفية حكمًا عليه، وتحصل على نتيجة، وتنقل النتيجة إلى الأسفل حتى تخرج الطبقة الأخيرة من الخلايا العصبية النتيجة.
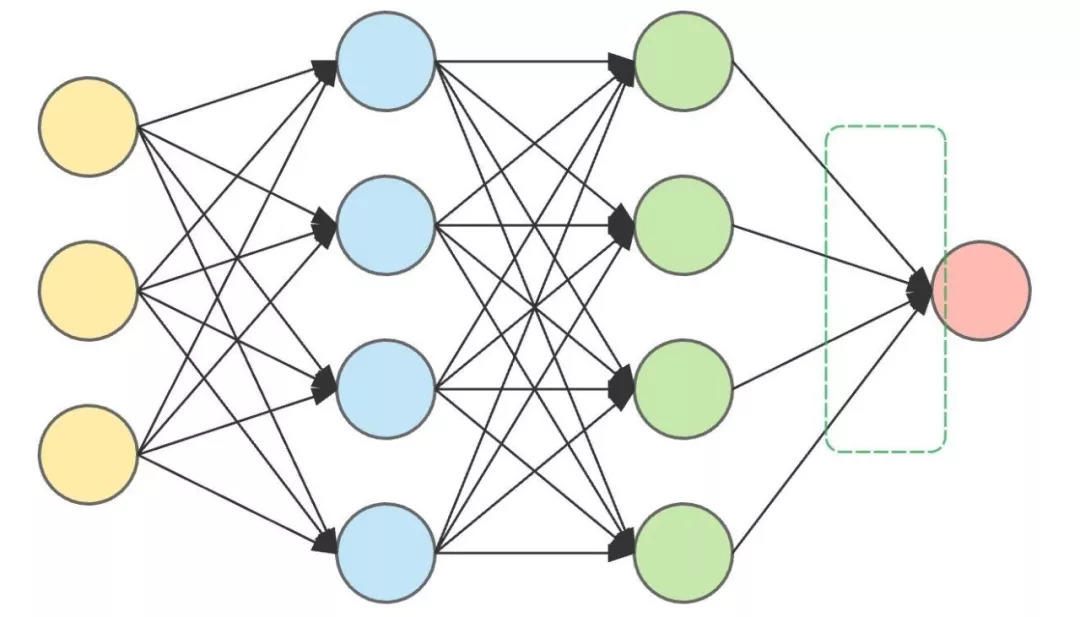
هذه هي بنية الشبكة العصبية الاصطناعية ذات الطبقتين المخفيتين.
تقع طبقة الإدخال (اليسار) وطبقة الإخراج (اليمين) على كلا الجانبين، وتقع الطبقتان المخفيتان في المنتصف.
إذا كان الحيوان بيولوجيًا قطة، لكن الشبكة العصبية الاصطناعية تقول إنه "ليس قطة"، فإن مخرجات الشبكة العصبية الاصطناعية خاطئة. الآن، الشيء الوحيد الذي يمكننا فعله هو العودة إلى الطبقة المخفية وضبط الأوزان والتحيزات، وهذه العملية من العودة وضبط البيانات هي الانتشار العكسي.
ومع ذلك، لتحقيق الانتشار العكسي، نحتاج أيضًا إلى الاعتماد على نوع مهم من الخوارزميات - خوارزمية الانحدار التدرجي. يؤدي النزول التدريجي إلى تسريع عملية التعلم بشكل كبير. يمكن فهم ذلك ببساطة على النحو التالي: عند النزول من الجبل من أعلى الجبل، فإن اختيار المسار الذي يحتوي على أكبر قدر من الانحدار هو الأسرع.
خوارزمية الانحدار التدرجي: مفتاح الانتشار العكسي
نظرًا لأننا نحتاج إلى حساب الانحراف بين الناتج والقيمة الفعلية باستمرار لتعديل المعلمات (كلما زاد الفرق، زاد التعديل)، نحتاج إلى استخدام دالة الخطأ (وتسمى أيضًا دالة الخسارة) لقياس الخطأ بين القيمة المتوقعة النهائية والقيمة الفعلية لجميع العينات في مجموعة التدريب.
في ي^ي هي نتيجة التنبؤ، yأنا للحصول على نتائج فعلية.
يقيس هذا التعبير الخطأ بين القيمة المتوقعة النهائية والقيمة الفعلية لجميع العينات في مجموعة التدريب، والتي تتعلق فقط بالفئة المتوقعة لطبقة الإخراج، ولكن هذه القيمة المتوقعة تعتمد على المعلمات في الطبقات السابقة. إذا لم نرغب في تصنيف الكلاب كقطط، فنحن بحاجة إلى تقليل دالة الخطأ هذه.
خوارزمية الانحدار المتدرج هي إحدى الخوارزميات التي تعمل على تقليل دالة الخطأ. وهي أيضًا خوارزمية تحسين شائعة الاستخدام في تدريب نموذج الشبكات العصبية الاصطناعية. تستخدم معظم نماذج التعلم العميق خوارزمية الانحدار التدريجي للتدريب على التحسين. بالنظر إلى مجموعة من معلمات الوظيفة، يبدأ الانحدار المتدرج من مجموعة أولية من قيم المعلمات ويتحرك بشكل تكراري نحو مجموعة من قيم المعلمات التي تقلل من دالة الخسارة. يتم تنفيذ هذا التقليل التكراري باستخدام حساب التفاضل والتكامل، مع أخذ تغييرات التدرج في الاتجاه السلبي للتدرج. المثال الكلاسيكي لاستخدام الانحدار المتدرج هو الانحدار الخطي. مع تكرار النموذج، تتقارب دالة الخسارة تدريجيًا إلى الحد الأدنى للقيمة.
نظرًا لأن التدرج يعبر عن اتجاه الحد الأقصى لمعدل تغير الدالة عند نقطة معينة ويتم الحصول عليه عن طريق حساب المشتق الجزئي، فإن استخدام طريقة الانحدار التدرجي سوف يسرع عملية التعلم بشكل كبير.
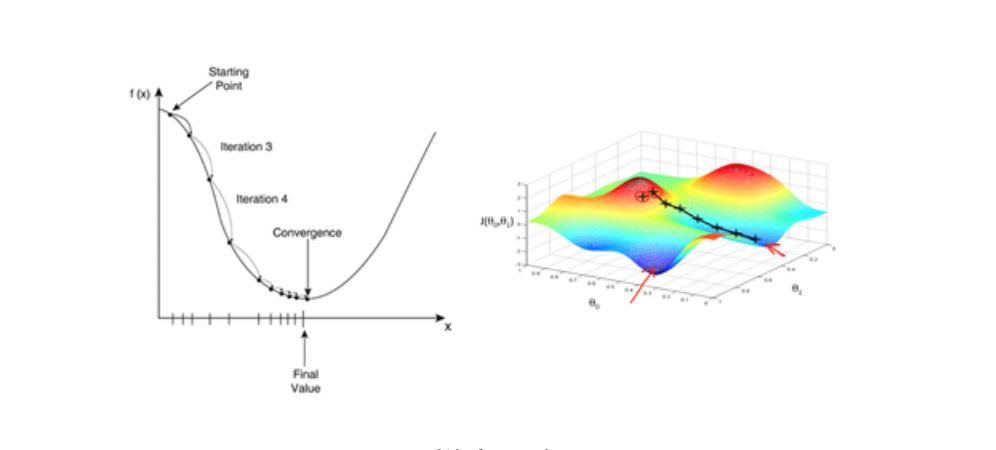
الانحدار التدريجي
من الناحية العملية، من المفيد نظريًا التحقق أولاً من كيفية تأثير قيم الوزن والتحيزات في الطبقة الأخيرة على النتيجة. من خلال أخذ المشتق الجزئي لدالة الخطأ E، يمكننا أن نرى تأثير قيم الأوزان والإزاحات على دالة الخطأ.
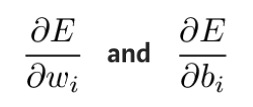
يمكن حساب هذه المشتقات الجزئية باستخدام قاعدة السلسلة لمعرفة كيفية تأثير التغييرات في هذه المعلمات على الناتج. صيغة الاشتقاق هي كما يلي:
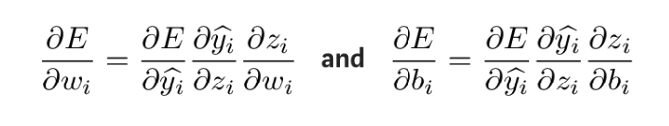
للحصول على الكمية المجهولة في التعبير أعلاه، خذ المشتق الجزئي لـ zi بالنسبة إلى wi وbi على التوالي:
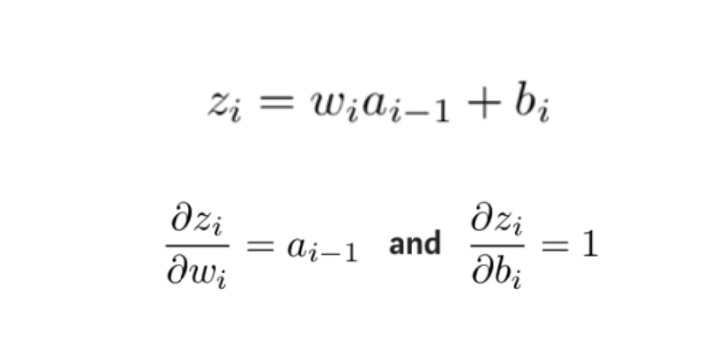بعد ذلك، يتم حساب المشتقات الجزئية لدالة الخطأ بالنسبة لأوزان وإزاحات كل طبقة بالترتيب العكسي، ويتم تحديث الأوزان والإزاحات المعدلة بطريقة الانحدار التدريجي حتى الطبقة الأولية التي يحدث فيها الخطأ.
هذه العملية هي خوارزمية الانتشار العكسي، والمعروفة أيضًا باسم خوارزمية BP، والتي تنشر خطأ طبقة الإخراج إلى الخلف طبقة تلو الأخرى، وتحديث معلمات الشبكة عن طريق حساب المشتقات الجزئية لتقليل دالة الخطأ، بحيث يمكن لخوارزمية ANN الحصول على الإخراج المتوقع.
في الوقت الحالي، يتم استخدام الانتشار الخلفي بشكل أساسي في خوارزميات الشبكات العصبية الاصطناعية في ظل التعلم الخاضع للإشراف.
القراءة الموسعة سوبر نيورو
أساسيات التعلم الآلي - المشتقات الجزئية:https://blog.csdn.net/qq_37527163/article/details/78171002
فهم الانتشار العكسي:https://blog.csdn.net/u012223913/article/details/68942581
سيرة جيفري هينتون:https://zh.wikipedia.org/wiki/%E6%9D%B0%E5%BC%97%E9%87%8C%C2%B7%E8%BE%9B%E9%A1%BF
http://www.cs.toronto.edu/~hinton/
دالة الخسارة:https://en.wikipedia.org/wiki/Loss_function
الخلايا العصبية البيولوجية:https://en.wikipedia.org/wiki/Neuron#Histology_and_internal_structure
وصف موجز لخوارزمية الانحدار التدرجي:https://blog.csdn.net/u013709270/article/details/78667531
مبدأ خوارزمية الشبكة العصبية الاصطناعية:http://www.elecfans.com/rengongzhineng/579673.html
كيفية تنفيذ الانحدار التدرجي:https://www.jianshu.com/p/c7e642877b0e