HyperAI超神经

يعد حل التعبيرات الرياضية موضوع بحث مهم للغاية في مجال التعلم الآلي، والانحدار الرمزي (SR) هو طريقة للعثور على التعبيرات الرياضية الدقيقة من البيانات.

يتم استخدام الانحدار الرمزي للكشف عن التعبير الرياضي الأساسي للبيانات الرصدية المعطاة. إنها تمتلك القدرة الطبيعية على التفسير والتعميم، ويمكنها تفسير الآليات السببية بين المتغيرات أو التنبؤ باتجاهات تطور الأنظمة المعقدة. كما يتم استخدامه على نطاق واسع في مجالات مختلفة مثل الفيزياء وعلم الفلك.

ومن التطبيقات الشهيرة اكتشاف كيبلر لمدارات الكواكب. استخدم العلماء خوارزميات الانحدار الرمزي لاكتشاف بعض القوانين الجديدة للحركة السماوية وبالتالي استنتاج مداراتها. وهذه مساهمة مهمة في استكشاف الإنسان للبحر الواسع من النجوم في الكون.

ومع ذلك، فإن البحث في الانحدار الرمزي يواجه أيضًا صعوباته الخاصة. يركز الانحدار الرمزي على الحصول على أفضل تركيبة من هذه العناصر وحل المعاملات الأكثر ملاءمة بالنظر إلى المتغيرات المستقلة X والمتغير التابع Y. ومع ذلك، فإن الحصول على أفضل تركيبة هي مشكلة صعبة من نوع NP (متعددة حدود غير حتمية)، وتنمو مساحة التركيبة بشكل كبير مع طول التعبير الرمزي. بالإضافة إلى ذلك، تتداخل عملية الحل غير الخطي للمعاملات وعملية تحسين تركيبة العناصر مع بعضها البعض، لذلك فإن تحديد التعبير الدقيق يستغرق وقتًا طويلاً للغاية.

ردا على هذه المشكلة الأكاديمية،اعتبر باحثون من معهد أشباه الموصلات التابع للأكاديمية الصينية للعلوم حل بنية التعبير كمشكلة تصنيف وحلوها من خلال التعلم الخاضع للإشراف، واقترحوا شبكة رمزية تسمى DeepSymNet لتمثيل التعبيرات الرمزية.بالمقارنة مع العديد من خوارزميات SR الشائعة المستندة إلى التعلم الخاضع للإشراف، يستخدم DeepSymNet تسميات أقصر، ويقلل من مساحة البحث التنبؤي، ويحسن من قوة الخوارزمية.

عنوان الورقة:
https://ieeexplore.ieee.org/document/10327762
اتبع الحساب الرسمي ورد "DeepSymNet" لتحميل الورقة

تم تسليط الضوء على حدود الأساليب الحالية

هناك حلين رئيسيين لبنية التعبير الرمزي الشائعة:

الحلول القائمة على البحث

الحل الكلاسيكي المبني على البحث هو خوارزمية GP (البرمجة الجينية). أولاً، يتم الحصول على العديد من التعبيرات بشكل عشوائي باعتبارها السكان الأوليين، ثم يتم إجراء التطور من خلال التكرار والتبادل والطفرة، ويتم اختيار النسل ذو الجودة الأصغر لمواصلة التطور حتى يلبي التعبير متطلبات الجودة.

بالإضافة إلى ذلك، من بين الطرق القائمة على البحث، هناك فئة مهمة من الطرق وهي استخدام التعلم التعزيزي للبحث عن هياكل التعبير المناسبة، مثل خوارزمية DSR، التي تقوم بتشفير شجرة الرموز على شكل تسلسل وتستخدم طريقة التدرج السياسي في التعلم التعزيزي العميق لحلها. الفكرة وراء DSR هي زيادة احتمالية أخذ عينات من التعبيرات ذات المكافآت الأكبر، وبالتالي إنتاج تعبيرات ذات أخطاء أصغر.

هناك أيضًا خوارزمية SR للصيغ الفيزيائية - AIFeynman، والتي تستخدم بشكل أساسي المعرفة السابقة في الفيزياء للحكم على بنية التعبير، وبالتالي تحليل التعبير إلى مشاكل فرعية أصغر وتضييق مساحة البحث؛ هناك طريقة أخرى تعتمد على التحسين المتفرق - EQL، تستخدم بشكل أساسي خوارزمية BP جنبًا إلى جنب مع التحسين المتفرق لتعلم المعلمات، وبالتالي الحصول على شبكة فرعية متفرقة في شبكة EQL، ثم الحصول على بنية التعبير الرياضي.

بالإضافة إلى عيوبها الواضحة، فإن هذا النوع من الطرق لديه عيب مشترك وهو البطء لأن مساحة البحث كبيرة ولا يمكن إعادة استخدام تجربة الحل.

حلول التعلم الخاضع للإشراف

يمكن للحلول القائمة على التعلم الخاضع للإشراف التغلب على العيوب التي تستغرق وقتًا طويلاً في الحلول القائمة على البحث. تتضمن الطرق التمثيلية SymbolicGPT وNeSymReS وE2E.

* يقوم SymbolicGPT بتشفير التعبيرات الرمزية في سلاسل ويعتبر حل بنية التعبير بمثابة مهمة ترجمة لغة. يستخدم نموذج GPT في عملية ترجمة اللغة عددًا كبيرًا من العينات المولدة بشكل مصطنع للتدريب الخاضع للإشراف؛

* يقوم NeSymReS بتشفير شجرة الرموز كتسلسل عبر العبور حسب الترتيب المسبق ويقوم بتدريبها باستخدام Set Transformer؛

* يقوم E2E بتشفير بنية التعبير والمعاملات في تسميات للتدريب، وبالتالي التنبؤ ببنية التعبير والمعاملات في وقت واحد.

ومع ذلك، فإن هذه الحلول تعاني من مشاكل تتعلق بالعلامات المكافئة المتعددة وعينات التدريب غير المتوازنة، والتي يمكن أن تسبب بسهولة غموضًا أثناء عملية التدريب وتؤثر على قوة الخوارزمية.بالإضافة إلى ذلك، لديهم عيوب أخرى. على سبيل المثال، يأخذ SymbolicGPT في الاعتبار التعبيرات البسيطة نسبيًا لأن عدد الرموز المستخدمة في أخذ العينات يصل إلى أربع طبقات على الأكثر؛ يقوم E2E بتشفير المعاملات على شكل علامات، مما يجعل العلامات طويلة جدًا ويؤثر على دقة التنبؤ، وما إلى ذلك.

نهج جديد لحل المشكلات - DeepSymNet

اقترح باحثون من معهد أشباه الموصلات التابع للأكاديمية الصينية للعلوم شبكة رمزية جديدة تسمى DeepSymNet لتمثيل التعبيرات الرمزية وقدموا الإطار العام لـ DeepSymNet.الطبقة الأولى هي البيانات، والطبقة الوسطى هي الطبقة المخفية، والطبقة الأخيرة هي طبقة الإخراج.

تتكون عقد الطبقة المخفية من رموز العمليات، بما في ذلك +، -، ×، ÷، sin، cos، exp، log، id، وما إلى ذلك، حيث يكون عامل id هو نفسه عامل id في EQL.

عدد مشغلي الهوية في كل طبقة مخفية يساوي عدد العقد في الطبقة السابقة، في حين تظهر المشغلات الأخرى مرة واحدة فقط في كل طبقة مخفية. يتوافق معرف المشغل واحدًا لواحد مع عقدة الطبقة السابقة، مما يتيح لكل طبقة الاستفادة من كافة المعلومات الموجودة في الطبقة السابقة. أما المشغلون الآخرون فهم مشغلون عاديون ومتصلون بشكل كامل بالطبقة السابقة.

إن الاتصال بين عامل المعرف والطبقة السابقة ثابت، وليس لدى العامل العادي أي اتصال بالطبقة السابقة، أو اتصال واحد أو اتصالين، مما يعني أنه في هذه الشبكة تمثل شبكة فرعية واحدة تعبيرًا رمزيًا واحدًا. كلما زاد عدد الطبقات المخفية التي تشغلها التعبيرات، زادت تعقيدات التعبير. لذلك، يمكن استخدام عدد الطبقات المخفية لقياس مدى تعقيد التعبير بشكل تقريبي.

ولكن يرجى ملاحظة أن طبقة الإدخال تحتوي على عقدة خاصة "const" والتي تستخدم لتمثيل المعاملات الثابتة في التعبيرات الرمزية. تحتوي الحواف المتصلة بالعقد "الثابتة" فقط على أوزان (معاملات ثابتة) لمنع ظهور عدد كافٍ من المعاملات الثابتة في التعبيرات الرمزية.

في المجمل،DeepSymNet هي شبكة كاملة يمكنها تمثيل أي تعبير. حل SR هي عملية البحث عن الشبكات الفرعية في DeepSymNet.

تظهر مجموعتان من المقارنات التجريبية المزايا

أجرى فريق البحث اختبارات تعتمد على مجموعات بيانات تم إنشاؤها بشكل مصطنع ومجموعات بيانات عامة، وقارن بين الخوارزميات الشائعة حاليًا.

عنوان تنزيل مجموعة البيانات:
https://hyper.ai/datasets/29321

في التجربة، يحتوي DeepSymNet على 6 طبقات مخفية على الأكثر ويدعم 3 متغيرات على الأكثر. قام فريق البحث بإنشاء 20 عينة لكل ملصق، تحتوي كل منها على 20 نقطة بيانات. فترة أخذ العينات لكل من المعاملات الثابتة والمتغيرات هي [-2,2]. تتمثل استراتيجية التدريب في التوقف المبكر (أي إيقاف التدريب عندما لا تنخفض الخسارة في مجموعة التحقق). بمساعدة آدم المحسن.

نتائج الاختبار على البيانات المولدة بشكل مصطنع

وتظهر نتائج الاختبار ما يلي:

* تزداد صعوبة التنبؤ مع زيادة عدد كائنات التنبؤ، وتزداد أيضًا الطبقة المخفية (أي التعقيد) للتعبير؛

* إن عنق الزجاجة في التنبؤ بالعلامة يكمن في اختيار المشغل؛

* DSN2 يحل الحلول المثالية والتقريبية بشكل أفضل من DSN1؛

* يمكن أن يؤدي دمج العلامات المكافئة وموازنة العينة إلى تعزيز قوة الخوارزمية.

أولاً،يمكن لـ DeepSymNet تمثيل التعبيرات بكفاءة أكبر من الأشجار الرمزية، وبالنسبة لنفس الوحدة التي تظهر عدة مرات في تعبير، يكون متوسط طول العلامة في DeepSymNet أقصر من متوسط طول العلامة في NeSymRes.

إن دقة التنبؤ للنموذج المدرب باستخدام علامات DeepSymNet تتجاوز بكثير دقة التنبؤ للنموذج المدرب باستخدام علامات NeSymReS، كما هو موضح في الشكل أعلاه. يوضح هذا أن علامات DeepSymNet أفضل من علامات الشجرة الرمزية.

ثانيًا،مع زيادة عدد الطبقات المخفية التي يشغلها التعبير، تنخفض دقة التنبؤ بالنموذج بسرعة. لذلك، اقترح فريق البحث تقسيم التنبؤ بالعلامة إلى مهمتين فرعيتين: التنبؤ بالمشغل والتنبؤ بعلاقة الاتصال، لضمان حل مشكلة التنبؤ بالعلامة بشكل أفضل.

تظهر نتائج تدريب DeepSymNet في جزأين أنه مع زيادة عدد الطبقات المخفية، تنخفض دقة التنبؤ باختيار المشغل بشكل حاد، في حين تظل دقة التنبؤ بعلاقات الاتصال مرتفعة. يرجع ذلك إلى أن مساحة اختيار المشغل أكبر بكثير من مساحة اختيار علاقة الاتصال. لذلك، من أجل تحسين دقة اختيار المشغل، أجرى الباحثون تدريبًا منفصلاً حول اختيار المشغل.

أثناء عملية التنبؤ، استخدم الفريق أولاً نموذج اختيار المشغل للحصول على تسلسل اختيار المشغل، ثم أدخله في النموذج المدرب DSN1 للتنبؤ بعلاقة الاتصال. وتظهر نتائج الاختبار في الشكل أعلاه. بعد التدريب المنفصل على اختيار المشغل، تحسنت دقة التنبؤ بشكل كبير. النموذج المدرب بشكل منفصل يسمى DSN2.

بالإضافة إلى ذلك، أجرى الباحثون تجارب الاستئصال للتحقق من قوة دمج العلامات المكافئة وتعزيز موازنة العينة. أولاً، تم اختيار 500000 عينة تدريبية بشكل عشوائي، تحتوي على 128455 تسمية مختلفة (TrainDataOrg). وتظهر النتائج أن أعداد العينات لهذه الملصقات موزعة بشكل غير متساوٍ، حيث يبلغ الحد الأدنى لعدد العينات 1، ويبلغ الحد الأقصى لعدد العينات 13196، ويبلغ تباين عدد العينات 13012.29.

ثم قام الفريق بموازنة عدد العينات للحصول على عينات التدريب TrainDataB وعينات التدريب TrainDataBM بعد دمج العلامات المكافئة.

وبعد ذلك، بناءً على بيانات التدريب الثلاثة، تم الحصول على النماذج DSNOrg وDSNB وDSNBM. تم اختبار هذه النماذج الثلاثة على مجموعة الاختبار. لقد زادت دقة النماذج الثلاثة من البداية إلى النهاية.يوضح هذا أنه بعد زيادة توازن العينة ودمج العلامات المكافئة، تم تحسين دقة النموذج في إيجاد الحل الأمثل، مما أدى بالفعل إلى تعزيز قوة الخوارزمية وتحسين أداء الخوارزمية.

نتائج اختبار مجموعة البيانات العامة

استخدم فريق البحث 6 مجموعات بيانات اختبارية:كوزا قام Korns وKeijzer وVlad وODE وAIFeynman باختيار التعبيرات بما لا يزيد عن 3 متغيرات من هذه المجموعات من البيانات للاختبار. تظهر المقارنة مع طرق التعلم الخاضع للإشراف الشائعة حاليًا أن دقة الخوارزميات المقترحة (DSN1، DSN2) متفوقة على خوارزميات المقارنة.

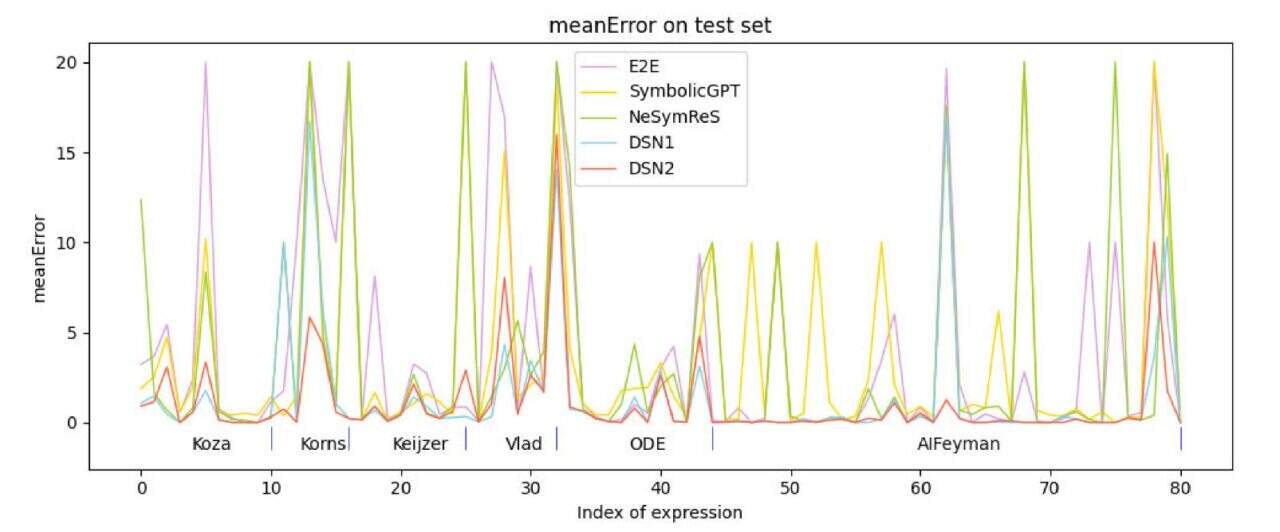
بالإضافة إلى ذلك، قام الفريق بمقارنة الخوارزمية مع طرق البحث الشائعة حاليًا EQL وGP وDSR، وتظهر النتائج في الشكل أدناه.

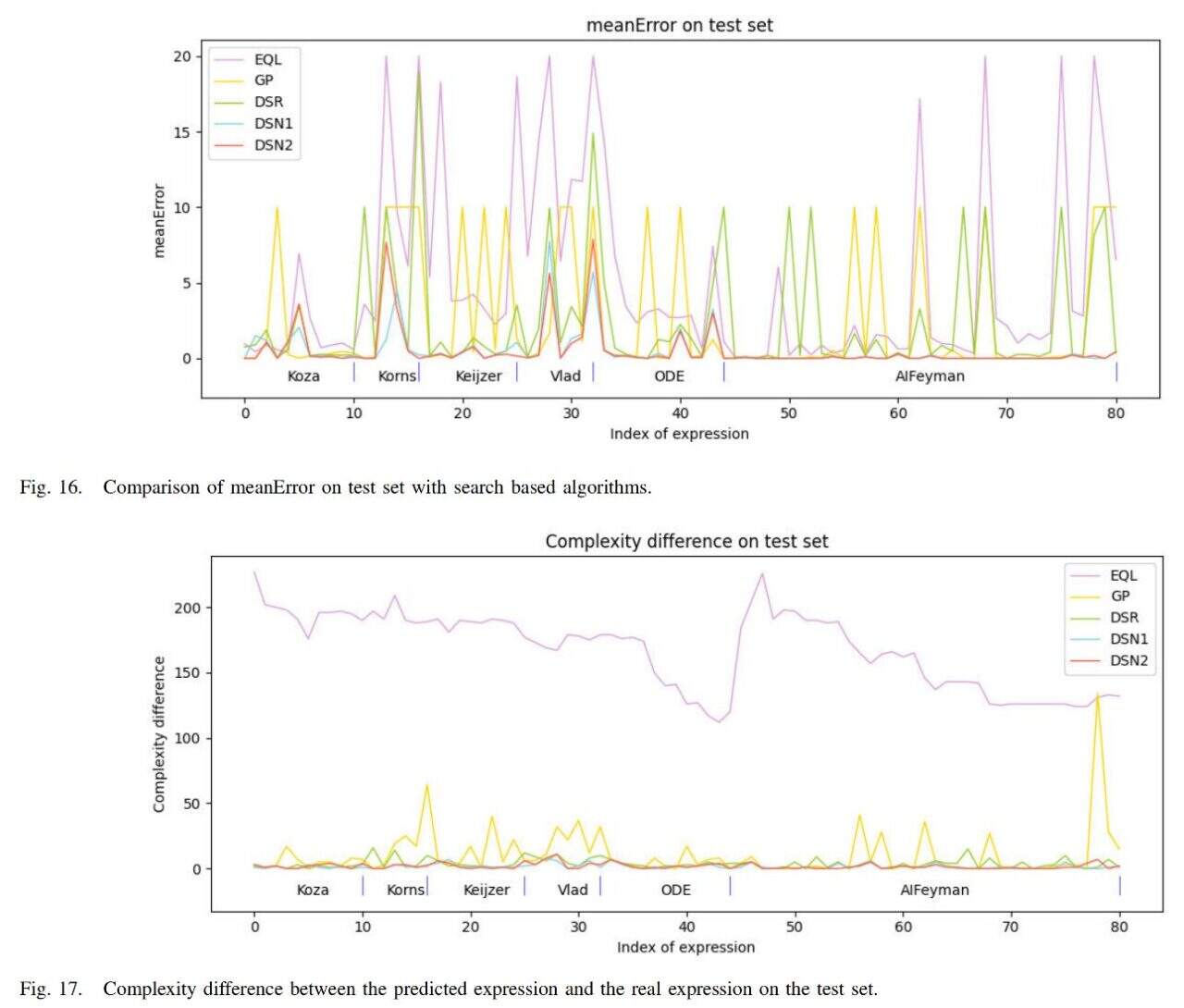
إن الخطأ المتوسط للخوارزمية (DSN1، DSN2) هو الأصغر، كما أن تعقيد التعبير الذي تم الحصول عليه هو الأقرب أيضًا إلى تعقيد التعبير الحقيقي.

باختصار، بناءً على النتائج، يمكن الاستنتاج أنوتتفوق الخوارزمية التي درسها الفريق على الخوارزميات المقارنة في ثلاثة جوانب: خطأ التعبير الرمزي، وتعقيد التعبير الرمزي، وسرعة التشغيل، مما يؤكد فعالية الخوارزمية.

الفريق خلف الكواليس مليء بالنجوم

ويعمل العلماء في مختلف أنحاء العالم بجهد على القضايا الأساسية المتعلقة بالانحدار الرمزي. وعلى الرغم من أن الورقة البحثية ذكرت أن DeepSymNet لا يزال لديه بعض القيود، إلا أن هذا البحث لا يزال يقدم مساهمة مهمة في الذكاء الاصطناعي في حل المشكلات الرياضية. ومن خلال التعامل معها كمشكلة تصنيف، فإنها توفر بلا شك حلاً جديدًا لطرق التعلم الذاتي القائمة على التعلم الخاضع للإشراف.

وبطبيعة الحال، فإن هذا الإنجاز لا ينفصل عن شغف وجهد مجموعة من الأشخاص، مثل وو مين، المؤلف الأول للبحث. وفقًا للموقع الرسمي لمعهد أشباه الموصلات التابع للأكاديمية الصينية للعلوم،وو مين هو حاليا باحث مساعد في معهد أشباه الموصلات، التابع للأكاديمية الصينية للعلوم. شارك في العديد من المشاريع البحثية العلمية، بما في ذلك "الانحدار الرمزي القائم على التعلم العميق وتطبيقه في البحث والتطوير لأجهزة أشباه الموصلات" و"طريقة الانحدار الرمزي لتبسيط تقسيم وغزو الشبكة العصبية لاندماج المعرفة".

فضلاً عن ذلك،كان الدكتور جينغي ليو، أحد مؤلفي الورقة البحثية، المؤلف الأول لورقة بحثية نُشرت في مجلة الذكاء الاصطناعي الرائدة Neural Networks في يوليو من العام الماضي. كان عنوان الورقة البحثية "SNR: إطار عمل التعلم القابل للتصحيح القائم على الشبكة الرمزية للانحدار الرمزي".يتم توفير إطار تعليمي مع إمكانيات التصحيح لمشكلة الانحدار الرمزي.

وبناء على الأبحاث التي أجريت حول المواضيع ذات الصلة، فإن البلاد تتصدر بقوة الأساليب المبتكرة. وما يمكن توقعه في المستقبل هو أن هذه النظريات ونتائج الأبحاث سوف تقدم بالتأكيد مساهمات مهمة في حل المشاكل العملية في المستقبل القريب.