AlphaGeometry: إن قوة الحوسبة الهائلة التي تتمتع بها DeepMind تخلق المعجزات مرة أخرى، ولكن "قوة الحوسبة بدلاً من الذكاء" قد لا تكون الحل الأمثل

المؤلف: لي باوزو

المحرر: سانيانغ

مصدر صورة الغلاف: Google DeepMind

هل تستخدم DeepMind قوة الحوسبة لخلق المعجزات؟ ما مدى قيمة برنامج AlphaGeometry الذي يحظى بالثناء الكبير؟

في الآونة الأخيرة، أضافت سلسلة Alpha من Google DeepMind عضوًا جديدًا - AlphaGeometry، الذي لا يزال يحظى بشعبية كبيرة، مع ثناء مثل "إنجاز تاريخي" و"ملحمي" و"قريب من البشر" على الشاشة. إذن، ما مقدار القيمة التي يتمتع بها نظام الذكاء الاصطناعي هذا، والذي يدعي امتلاك قدرات على مستوى الميدالية الذهبية في أولمبياد الرياضيات؟

تم تطوير AlphaGeometry بواسطة فريق Google DeepMind وباحثين من جامعة نيويورك.الجمع بين نموذج اللغة العصبية ومحرك الاستنتاج الرمزي،القدرة على حل المشاكل الهندسية المعقدة على مستوى قريب من مستوى البشر.

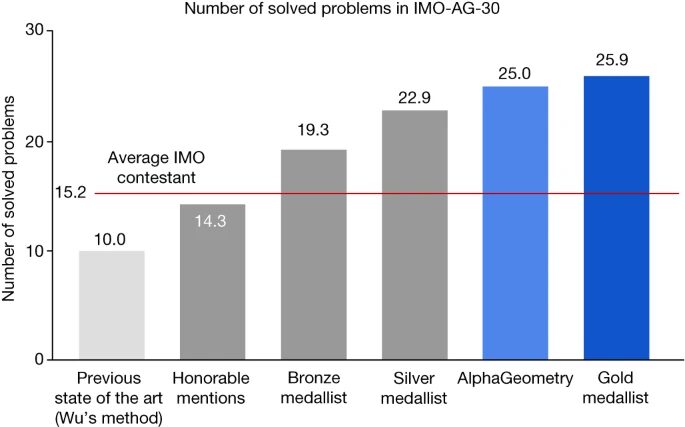
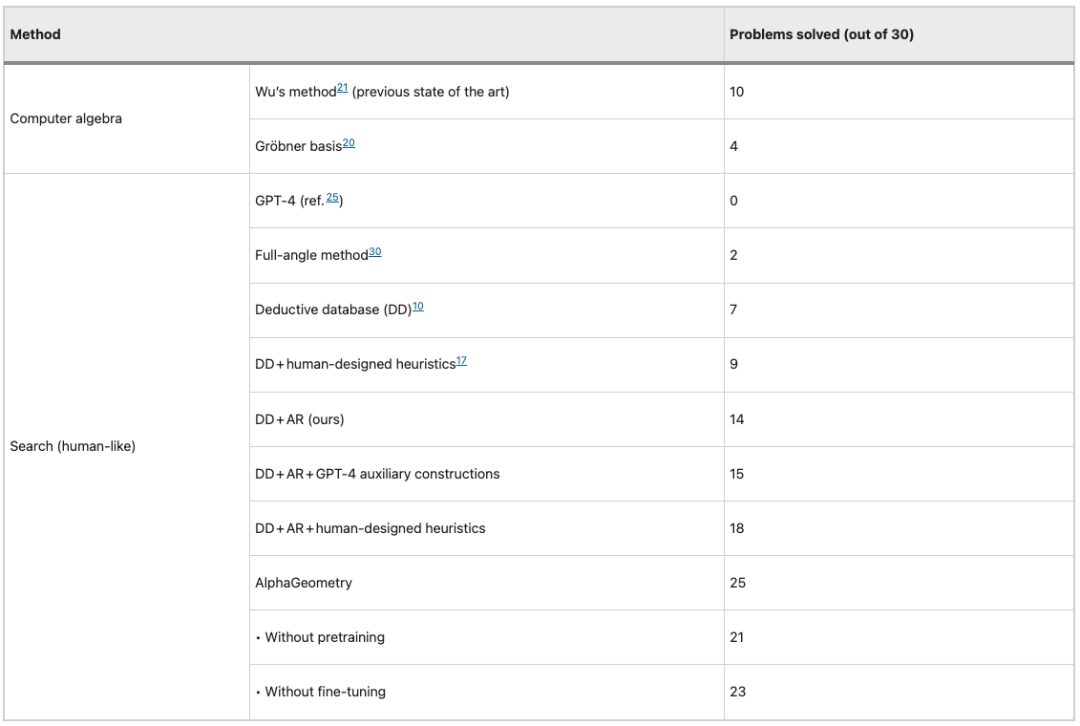
في اختبار معياري لـ 30 مسألة هندسية من مسائل أولمبياد الرياضيات الدولي (IMO)، تمكن AlphaGeometry من حل 25 منها في الوقت المحدد، والذي كان في السابق سوتا  تمكنت "طريقة وو" الخاصة بـ وو من حل 10 مسائل، في حين تمكن الحائز على الميدالية الذهبية في المنظمة البحرية الدولية من حل 25.9 مسألة في المتوسط.

في الواقع، منذ إطلاق AlphaGo، مصحوبًا بالعديد من الاختراقات المبتكرة في مختلف التخصصات، ترسخت فكرة "يجب أن تكون منتجات DeepMind عالية الجودة" تدريجيًا في أذهان الناس. ولكن في الوقت نفسه، هناك أيضًا أصوات عقلانية وجدلية في الصناعة - إن استبدال الذكاء بقوة الحوسبة أمر مُرضٍ بالتأكيد، ولكن القيمة التطبيقية الفعلية أكثر أهمية. لذلك، مع إصدار AlphaGeometry، نود أن نناقش بإيجاز ما إذا كان هذا بمثابة كرنفال في ظل ميزة قوة الحوسبة، أو الذكاء الاصطناعي للعلوم  مستكشف.

ومن الجدير بالذكر أنأجرينا مقابلة مع أستاذ في كلية الاستخبارات بجامعة بكينلين تشوتشن، وناقشنا ودرسنا القضايا الأكاديمية ذات الصلة.درس البروفيسور لين تشوتشين الرياضيات والرياضيات التطبيقية في جامعة نانكاي وجامعة بكين وجامعة هونغ كونغ للفنون التطبيقية، ثم عاد إلى كلية الرياضيات في جامعة بكين للحصول على درجة الدكتوراه وبدأ في دخول مجال الذكاء الاصطناعي. (انقر هنا لمشاهدة المقابلة مع البروفيسور لين تشوتشين)

التعبير والحساب: تحديان رئيسيان للذكاء الاصطناعي في الرياضيات

وقال البروفيسور لين تشوتشن:"في الماضي، كان "التعبير" عن النظريات الرياضية والحوسبة واسعة النطاق هما التحديان الرئيسيان للذكاء الاصطناعي لإثبات النظريات الرياضية."

أولًا، ولأن الرياضيات مجالٌ تجريديٌّ يعتمد بشكلٍ كبير على التفكير المنطقي، فإن الخطوة الأولى لاحتضان الذكاء الاصطناعي في الرياضيات هي حل مشكلة "التعبير". ويُعدّ التعبير عن النظريات الرياضية بطريقةٍ تُمكّن الحواسيب من حسابها أساسًا لتطبيقات الذكاء الاصطناعي اللاحقة.

إن المشكلات الهندسية التي يستهدفها AlphaGeometry من السهل نسبيًا التعبير عنها. لقد أدى ظهور الهندسة التحليلية والهندسة الجبرية إلى إمكانية التعبير عن الأشكال الهندسية والعلاقة بين الأشكال الهندسية من خلال القيم العددية.وو ونجونال "الميكنة الرياضية"وإلى حد ما، قامت أيضًا ببناء جسر بين نظريات الهندسة المستوية ولغة الآلة."

ثانيًا، حلّ أسلوب وو الذي اقترحه الأكاديمي وو ونجون، بالإضافة إلى أساليب تقليدية مثل قاعدة غروبنر، مشكلة إثبات نظريات الهندسة المستوية نظريًا، إلا أن قدرتها الحسابية محدودة. بمعنى آخر، نظرًا لحجم التخزين والحوسبة الكبير، وخاصةً عند مواجهة مسائل هندسة مستوية أكثر تعقيدًا، ستزداد مساحة التشغيل بشكل كبير، لذا تواجه العديد من الأساليب السابقة صعوبة في معالجة المسائل المعقدة.

من الواضح أن مشكلة كمية كبيرة من العمليات الحسابية ليست العقبة الرئيسية أمام DeepMind، التي تتمتع بموارد مالية كبيرة. تكمن الصعوبة الرئيسية في كيفية تجنب النمو الهائل لمساحة التشغيل، وهنا يمكن أن تساعد أساليب التعلم الآلي. "

على وجه التحديد، تم تدريب AlphaGeometry على 100 مليون نقطة بيانات اصطناعية، ويمكنه حل التحديات الهندسية المعقدة بشكل مستقل دون عروض بشرية، وإنشاء أدلة يمكن قراءتها بواسطة الإنسان.

كما هو موضح في الشكل أدناه، مع الأخذ في الاعتبار "نظرية متساوي الساقين" الأكثر شيوعًا بين طلاب المدارس الابتدائية والثانوية في بلدي كمثال، إذا كنت تريد إثبات أن ∠ABC = ∠BCA، فأنت بحاجة إلى تحويل المشكلة يدويًا إلى لغة الكمبيوتر أولاً، ثم إدخالها في AlphaGeometry.

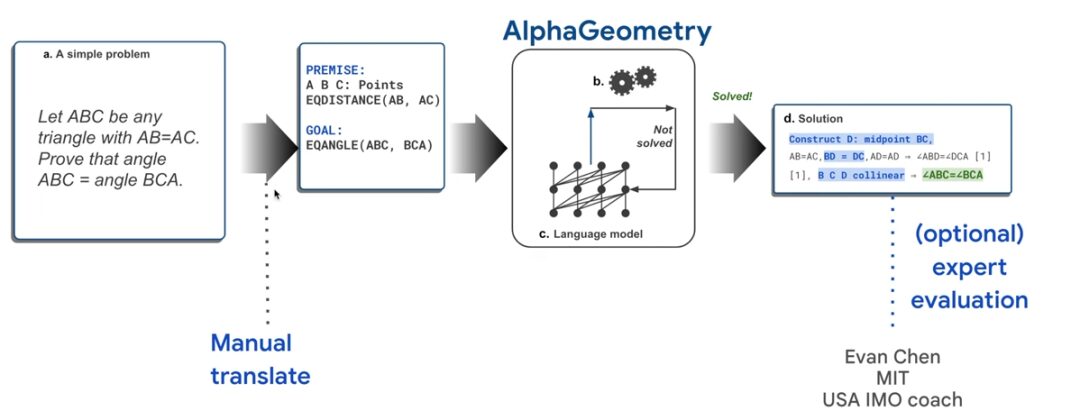
تبدأ AlphaGeometry عملية البحث عن الإثبات من خلال تشغيل محرك استنتاج رمزي يستنتج "بشكل شامل" عبارات جديدة من مقدمات النظرية حتى يتم إثبات النظرية أو استنفاد العبارات الجديدة. إذا فشل محرك الاستنتاج الرمزي في العثور على دليل، يقوم نموذج اللغة بإنشاء نقطة مساعدة، وإضافة شروط قابلة للإثبات، وإعادة تشغيل البحث عن دليل من خلال المحرك الرمزي. تستمر هذه الدورة حتى يتم العثور على الحل.

سيتم تحليل الحلول تلقائيًا إلى لغة يمكن للإنسان قراءتها، حتى يمكن التحقق منها وتقييمها.

ومن الجدير بالذكر أن AlphaGeometry يستخدم البيانات الاصطناعية لتدريب النموذج، مما يحل مشكلة نقص قواعد البيانات ذات الصلة.

وباستخدام المحرك الرمزي الموجود على فرضيات نظرية عشوائية مختلفة وتشغيله على 100 ألف وحدة معالجة مركزية لمدة 72 ساعة، حصل الباحثون على ما يقرب من 500 مليون مثال لإثبات النظرية الاصطناعية. وبعد التطبيع الرسمي وإزالة التكرار، حصلوا في النهاية على 100 مليون مثال لإثبات النظرية، منها 9 ملايين مثال تضمنت على الأقل بناء مساعد واحد، وتجاوزت العديد من خطوات الإثبات 200 خطوة، وهو ما يعادل أربعة أضعاف متوسط طول الإثبات لمشاكل الهندسة في الأولمبياد الدولي للرياضيات.

من أجل مقارنة واختبار قدرة AlphaGeometry على حل المشكلات العملية، حاول الباحثون تحويل مشاكل الهندسة في مسابقة IMO منذ عام 2000 إلى لغة آلية قابلة للقراءة بواسطة المحركات الرمزية، ووجدوا أنه يمكن التعبير عن 75% فقط بنجاح، وبالتالي تشكيل مجموعة اختبار IMO-AG-30 تتكون من 30 مشكلة هندسية كلاسيكية.

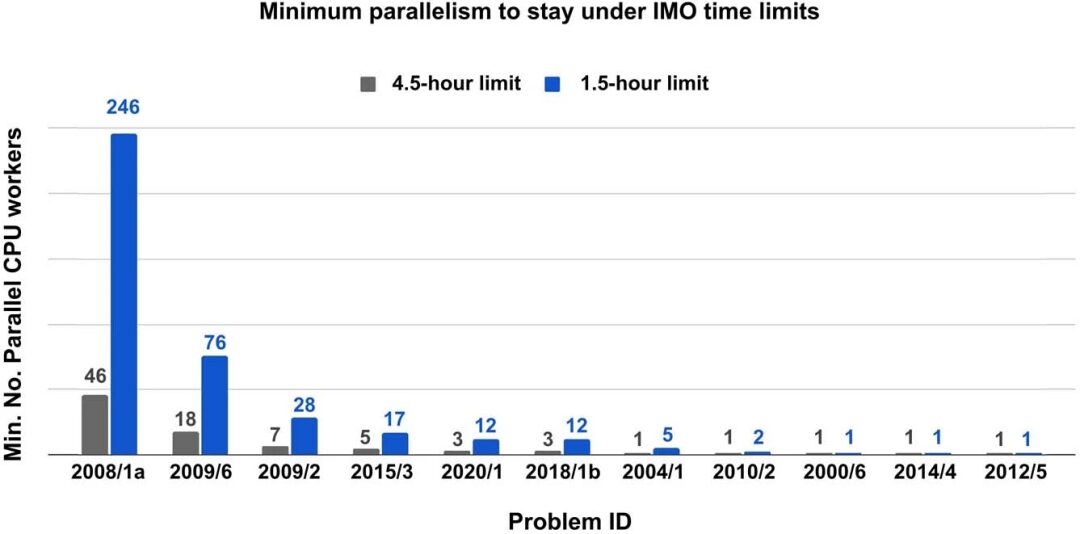
تتمتع كل مشكلة بوقت تشغيل مختلف لأن حجم إغلاق الاشتقاق الخاص بها مختلف. ووجد الباحثون أن وقت الجري لا يرتبط بمدى صعوبة المشكلة. على سبيل المثال، تعد IMO 2019 P6 أكثر صعوبة بكثير من IMO 2008 P1a، ولكنها تتطلب وقت توازي أقل بكثير لحلها ضمن الحد الزمني لـ IMO.

نظرًا لأن عملية فك تشفير نموذج اللغة تعيد k تسلسلات مختلفة، تصف k من الهياكل المساعدة الاختيارية، فقد أجرى الباحثون بحثًا شعاعيًا على k خيارات، باستخدام درجة كل شعاع كدالة قيمة له. تتمتع هذه الطريقة بالتوازي القوي ويمكنها تحسين سرعة البحث بشكل كبير عندما تكون موارد الحوسبة المتوازية متاحة.

وجد الباحثون أن الحد الأدنى لعدد وحدات المعالجة المركزية المتوازية المطلوبة لحل جميع المشكلات الـ 25 والبقاء ضمن الحد الزمني مع أربع نسخ متوازية من نموذج اللغة المعجل GPU V100 موضح في الشكل التالي:

يظهر في الشكل أدناه أداء 10 نماذج/طرق مختلفة على مجموعة اختبار IMO-AG-30. ومن المثير للاهتمام أن GPT-4 لم يتمكن من الإجابة بشكل صحيح على سؤال واحد في الاختبار.

وراء استبدال قوة الحوسبة بالذكاء، فإن قيمة التطبيق هي المفتاح

خلال اليومين الماضيين، كشفت التقارير الساحقة على شبكة الإنترنت عن الإنجازات الكاملة التي حققتها AlphaGeometry. لا يحتاج تأثيرها إلى تفصيل، لذلك نود أن نستكشف، بعد كل هذا الضجيج، ما هي القيمة العملية التي يمكن أن تضيفها AlphaGeometry إلى البحث العلمي وتطوير تطبيقات الذكاء الاصطناعي؟

وقال البروفيسور لين تشوتشن:في الوقت الحاضر، يمكن لـ AlphaGeometry أن يصبح "معلمًا" مثل AlphaGo ويلعب دورًا مساعدًا أكبر في التدريس.وعلاوة على ذلك، فإن الاختراق الذي أحرزته شركة AlphaGeometry في أداء النماذج أمر لا يمكن إنكاره، وهو يوضح كذلك أن "القوة العظيمة يمكن أن تخلق المعجزات" - حيث تعمل ميزة قوة الحوسبة القوية على خلق أداء قوي للنماذج، وهو ما يضيف إلى حد ما مزيدًا من الثقة للباحثين والشركات الذين "يعبدون" قوة الحوسبة. "

ومع ذلك، كما قال البروفيسور لين تشوتشين،في مجال الذكاء الاصطناعي، وعلى الرغم من أننا شهدنا فعالية "استبدال الذكاء بقوة الحوسبة" مرات لا تحصى، فإن الاختراق النهائي 1% نحو أن نصبح خبراء في الصناعة لا يزال من الصعب تحقيقه باستخدام الذكاء الاصطناعي.

لذلك، في الوقت الراهن، سواء كان الأمر يتعلق بـ AlphaGeometry أو أدوات الذكاء الاصطناعي الأخرى مثل نموذج GPT، فإنها لا تزال "معلمين وأصدقاء" في الحياة اليومية للناس والبحث العلمي. أصبح الاستخدام المرن لأدوات الذكاء الاصطناعي اتجاهًا عامًا. إن كيفية تطبيق "المعجزة" التي تخلقها قوة الحوسبة على المشاكل العملية هي قيمة الإنسان التي يصعب استبدالها.

من خلال استخلاص الدروس من الماضي وتطبيقها على الحاضر، فإن الارتفاع السريع لأدوات الذكاء الاصطناعي يتشابه إلى حد كبير مع انتشار أجهزة الكمبيوتر. على سبيل المثال، أحدثت ثورة في طريقة عملنا، واستبدلت الأساليب التقليدية بزخم كبير وأصبحت تدريجيا معيارا لتقييم قدرات مكان العمل... ولكن في المقابل، فإن قيود أدوات الذكاء الاصطناعي أكثر وضوحا أيضا، أي الخصوصية.

يعتقد البروفيسور لين تشوتشين:تفتقر أدوات الذكاء الاصطناعي الحالية إلى التوحيدحتى لو ركزنا فقط على الرياضيات، هناك فرق كبير بين أدوات الذكاء الاصطناعي التي تم تطويرها لنظرية الأعداد والهندسة، ناهيك عن أدوات الذكاء الاصطناعي متعددة التخصصات. إن أدوات الذكاء الاصطناعي ليست متاحة بعد مثل البنية التحتية الأساسية التي تتمتع بها أجهزة الكمبيوتر اليوم. تشمل لغات الكمبيوتر الحالية C وJava وPython وغيرها. ومن الممكن تمامًا حل المشكلات في تخصصات متعددة مثل الرياضيات والفيزياء والكيمياء وما إلى ذلك بناءً على أي من هذه اللغات، مما يعكس تنوعها. ومع ذلك، ليس هذا هو الحال مع أدوات الذكاء الاصطناعي، كما يمكن رؤيته من سلسلة Alpha. "

لذلك، يعتقد البروفيسور لين تشوتشن أنه: "في المستقبل، عندما يمكن تجريد أدوات الذكاء الاصطناعي وإعادة استخدامها، فإن الذكاء الاصطناعي للعلوم سيكون قادرًا على أن يصبح شائعًا". "

وهذه أيضًا ظاهرة لاحظتها شركة HyperAI أثناء تتبعها المستمر لتطور الذكاء الاصطناعي في مجال العلوم. بعض مجموعات البحث أو فرق البحث سوف تقوم بتجنيد عضو متخصص في الذكاء الاصطناعي بالإضافة إلى أعضاء التخصص ليكون مسؤولاً عن تطوير أدوات الذكاء الاصطناعي اللازمة للبحث، في حين لا يزال الجزء العلمي متروكًا للباحثين العلميين التقليديين.

ليس هناك شك في أن مساعدة الذكاء الاصطناعي وتحسينه لعملية البحث العلمي أصبح واضحًا بشكل متزايد وأصبح اتجاهًا جديدًا، ولكن هل يعتبر نموذج فريق الذكاء الاصطناعي + العلم حلاً طويل الأمد؟

يعتقد البروفيسور لين تشوتشن: "في المستقبل، من ناحية، يجب خفض عتبة استخدام أدوات الذكاء الاصطناعي وتحقيق درجة معينة من التوحيد، حتى يتمكن العلماء أيضًا من الجمع بين مكونات أدوات الذكاء الاصطناعي واستخدامها لحل مشاكل مختلفة، تمامًا مثل برمجة الكمبيوتر؛ من ناحية أخرى، يحتاج العلماء أيضًا إلى تحسين قدرتهم تدريجيًا على استخدام أدوات الذكاء الاصطناعي من أجل إطلاق العنان لقوة الذكاء الاصطناعي".

الطريق طويل وصعب، ولكن إذا واصلت المسير فسوف تصل إلى وجهتك. لقد تم إطلاق الذكاء الاصطناعي للعلوم من قبل شركات كبرى مثل DeepMind، ومع تعزيز السياسات الوطنية، بدأ رحلة طويلة. إن الأشواك في هذه الرحلة تحتاج إلى إزالتها من خلال البحث العلمي والصناعة معًا لخلق قيمة حقيقية للتنمية البشرية في تنفيذها.

وأخيرا، أود أن أشكر البروفيسور لين تشوتشين من كلية الاستخبارات بجامعة بكين على مساعدته ودعمه في كتابة هذا المقال. في الوقت الحالي، تقوم مجموعة البحث التابعة للأستاذ الدكتور تشوتشين لين بتجنيد طلاب الدكتوراه. يمكن للطلاب الذين يستوفون المتطلبات إرسال سيرتهم الذاتية إلى: zlin@pku.edu.cn

أنا أعيش وفقا لمبدأ الفيزيائي لودفيج بولتزمان: لا يوجد شيء أكثر عملية من النظرية الجيدة. أبحث الآن عن طلاب دكتوراه أقوياء في الرياضيات (ولكن هذا لا يعني أنه يجب أن تكون من قسم الرياضيات) ومهتمين جدًا بالتحليل النظري، حتى يتمكنوا من الاستمتاع معي بكيفية استخدام الرياضيات بأناقة لحل المشكلات العملية. مرحبا بكم في إرسال سيرتك الذاتية.

——لين تشوتشين