シグモイド関数シグモイド関数
シグモイド関数シグモイド関数は一般的な S 字関数であり、S 字成長曲線とも呼ばれます。単一増加や逆関数単一増加などの特性により、0 と 2 の間の変数をマッピングするニューラル ネットワークのしきい値関数としてよく使用されます。 1.
シグモイド関数の基本的な性質
シグモイド関数の形式とイメージは次のとおりです。
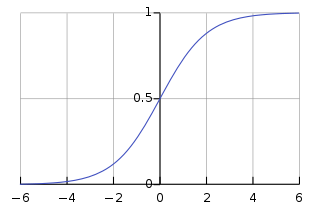
- ドメイン: (−∞、+∞);
- 値の範囲: (− 1 , 1 );
- この関数は、定義領域内の連続的な滑らかな関数です。
- どこでも微分可能であり、導関数は次のようになります。 f' ( x ) = f ( x ) ( 1 − f ( x ) );
- 関数の値の範囲は 0 から 1 で、0.5 で中心対称になり、値が x = 0 に近づくほど傾きが大きくなります。
シグモイド関数とロジスティック回帰
ロジスティック回帰 LR の目的に応じて、関数を選択する際には次の 2 つの条件を満たす必要があります。
1) 値の範囲は 0 ～ 1 です。
2) イベント発生の場合、50% が結果の分水界であり、選択関数は 0.5 の中心の周りで対称である必要があります。
これら 2 つの点に基づいて、Sigmoid は LR のニーズを正確に満たします。