Command Palette
Search for a command to run...
シリコンの状態密度とエネルギーバンドのVASPハイブリッド関数計算
ウィーン第一原理シミュレーションパッケージ (VASP) これは、電子構造計算や量子力学的分子動力学など、第一原理から原子スケールの材料モデリングを行うコンピュータ プログラムです。
VASP は、多体シュレーディンガー方程式の近似解を計算するのに適しています。密度汎関数理論 (DFT) の枠組み内でコーン・シャム方程式を解いたり、ハートリー・フォック (HF) 近似でルートハーン方程式を処理したりするなど、さまざまな計算手法をカバーしています。 VASP のもう 1 つの革新は、ハートリー・フォック法と密度汎関数理論を統合してハイブリッド汎関数法を形成し、研究者により柔軟な計算オプションを提供することです。さらに、グリーン関数法 (GW 準粒子および ACFDT-RPA) と多体摂動論 (2 次 Møller-Plesset) も VASP で利用できます。
VASP では、単一電子軌道、電子電荷密度、局所ポテンシャルなどの中心量は、平面波基底セットを使用して表されます。電子とイオン間の相互作用は、ノルム保存則、超ソフト擬ポテンシャル、またはプロジェクター増強波動法を使用して記述されます。
VASP は、電子の基底状態を決定するために、直接反転反復サブスペースを使用した残差最小化法 (RMM-DIIS) やブロック Davidson アルゴリズムなどの効率的な反復行列対角化手法を利用します。これらは、効率的な Broyden および Pulay 密度混合スキームと組み合わされ、自己無撞着ループを加速します。
チュートリアルの紹介
このチュートリアルでは、ハイブリッド関数を使用してシリコンエネルギーバンドを計算する方法を学びます。これは、前のチュートリアル(VASP 入門チュートリアル: シリコンの状態密度と帯域幅の計算)では、ハイブリッド関数は正しいバンドギャップを持つ物質のエネルギーバンドと状態密度を計算することができますが、より多くの計算リソースが必要になるため、今回はデモに GPU を使用しています。
このチュートリアルに従うことで、VASP ハイブリッド機能計算に必要な INCAR と KPOITNS を生成する方法を学習します。
前回のチュートリアル(VASP 入門チュートリアル: シリコンの状態密度と帯域幅の計算)には 4 つのステップがあります。このハイブリッド関数の計算では、シリコンの状態密度とエネルギー バンドを取得するために 1 つのステップのみが必要です (構造最適化はスキップされます)。
入力ファイルの準備
このチュートリアルでは、INCAR、POSCAR、KPOINTS、POTCAR の 4 つのファイルを準備する必要があります。
インカール
Global Parameters
ENCUT = 300 (波函数截断能量)
PREC = Normal (精度设置)
LWAVE = .TRUE. (保存波函数)
LCHARG = .TRUE. (保存电荷)
ADDGRID= .TRUE. (增加格点加速收敛)
Static Calculation
ISMEAR = 0 (高斯占据数)
SIGMA = 0.1 (高斯展宽)
LORBIT = 11 (输出 DOSCAR 和 PROCAR)
NELM = 60 (最大电子步)
EDIFF = 1E-08 (电子步收敛判据)
HSE06 Calculation
LHFCALC= T (启动杂化泛函计算)
AEXX = 0.25 (杂化比例 0.25)
HFSCREEN= 0.2 (杂化屏蔽参数 0.2)
ALGO = ALL (最优化算法)
TIME = 0.4 (最优化算法步长)
PRECFOCK= N (FFT 精度)
ポスカー
Si #(体系名称)
1.0 #(放大系数 下面 3 行对应 3 个晶格矢量 )
0.0 2.75 2.75
2.75 0.0 2.75
2.75 2.75 0.0
Si #(元素)
2 #(对应元素原子数)
Direct #(采用分数坐标,下列为 2 个原子的分数坐标)
0 0 0
0.25 0.25 0.25
Kポイント
0.060 5 5 5 10 0.060 83 6 19 6 20 16 13 9 # Parameters to Generate KPOINTS (Do NOT Edit This Line)
93
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.20000000000000 0.00000000000000 0.00000000000000 8
0.40000000000000 0.00000000000000 0.00000000000000 8
0.20000000000000 0.20000000000000 0.00000000000000 6
0.40000000000000 0.20000000000000 0.00000000000000 24
-0.40000000000000 0.20000000000000 0.00000000000000 24
-0.20000000000000 0.20000000000000 0.00000000000000 12
0.40000000000000 0.40000000000000 0.00000000000000 6
-0.40000000000000 0.40000000000000 0.00000000000000 12
-0.40000000000000 0.40000000000000 0.20000000000000 24 (以上为 scf 点位)
0.00000000000000 0.00000000000000 0.00000000000000 0 (以下为能带点位)
0.02777777777778 0.00000000000000 0.02777777777778 0
0.05555555555556 0.00000000000000 0.05555555555556 0
0.08333333333333 0.00000000000000 0.08333333333333 0
0.11111111111111 0.00000000000000 0.11111111111111 0
0.13888888888889 0.00000000000000 0.13888888888889 0
0.16666666666667 0.00000000000000 0.16666666666667 0
0.19444444444444 0.00000000000000 0.19444444444444 0
0.22222222222222 0.00000000000000 0.22222222222222 0
0.25000000000000 0.00000000000000 0.25000000000000 0
0.27777777777778 0.00000000000000 0.27777777777778 0
0.30555555555556 0.00000000000000 0.30555555555556 0
0.33333333333333 0.00000000000000 0.33333333333333 0
0.36111111111111 0.00000000000000 0.36111111111111 0
0.38888888888889 0.00000000000000 0.38888888888889 0
0.41666666666667 0.00000000000000 0.41666666666667 0
0.44444444444444 0.00000000000000 0.44444444444444 0
0.47222222222222 0.00000000000000 0.47222222222222 0
0.50000000000000 0.00000000000000 0.50000000000000 0
0.50000000000000 0.00000000000000 0.50000000000000 0
0.52500000000000 0.05000000000000 0.52500000000000 0
0.55000000000000 0.10000000000000 0.55000000000000 0
0.57500000000000 0.15000000000000 0.57500000000000 0
0.60000000000000 0.20000000000000 0.60000000000000 0
0.62500000000000 0.25000000000000 0.62500000000000 0
0.37500000000000 0.37500000000000 0.75000000000000 0
0.35526315789474 0.35526315789474 0.71052631578947 0
0.33552631578947 0.33552631578947 0.67105263157895 0
0.31578947368421 0.31578947368421 0.63157894736842 0
0.29605263157895 0.29605263157895 0.59210526315789 0
0.27631578947368 0.27631578947368 0.55263157894737 0
0.25657894736842 0.25657894736842 0.51315789473684 0
0.23684210526316 0.23684210526316 0.47368421052632 0
0.21710526315789 0.21710526315789 0.43421052631579 0
0.19736842105263 0.19736842105263 0.39473684210526 0
0.17763157894737 0.17763157894737 0.35526315789474 0
0.15789473684211 0.15789473684211 0.31578947368421 0
0.13815789473684 0.13815789473684 0.27631578947368 0
0.11842105263158 0.11842105263158 0.23684210526316 0
0.09868421052632 0.09868421052632 0.19736842105263 0
0.07894736842105 0.07894736842105 0.15789473684211 0
0.05921052631579 0.05921052631579 0.11842105263158 0
0.03947368421053 0.03947368421053 0.07894736842105 0
0.01973684210526 0.01973684210526 0.03947368421053 0
0.00000000000000 0.00000000000000 0.00000000000000 0
0.00000000000000 0.00000000000000 0.00000000000000 0
0.03333333333333 0.03333333333333 0.03333333333333 0
0.06666666666667 0.06666666666667 0.06666666666667 0
0.10000000000000 0.10000000000000 0.10000000000000 0
0.13333333333333 0.13333333333333 0.13333333333333 0
0.16666666666667 0.16666666666667 0.16666666666667 0
0.20000000000000 0.20000000000000 0.20000000000000 0
0.23333333333333 0.23333333333333 0.23333333333333 0
0.26666666666667 0.26666666666667 0.26666666666667 0
0.30000000000000 0.30000000000000 0.30000000000000 0
0.33333333333333 0.33333333333333 0.33333333333333 0
0.36666666666667 0.36666666666667 0.36666666666667 0
0.40000000000000 0.40000000000000 0.40000000000000 0
0.43333333333333 0.43333333333333 0.43333333333333 0
0.46666666666667 0.46666666666667 0.46666666666667 0
0.50000000000000 0.50000000000000 0.50000000000000 0
0.50000000000000 0.50000000000000 0.50000000000000 0
0.50000000000000 0.47916666666667 0.52083333333333 0
0.50000000000000 0.45833333333333 0.54166666666667 0
0.50000000000000 0.43750000000000 0.56250000000000 0
0.50000000000000 0.41666666666667 0.58333333333333 0
0.50000000000000 0.39583333333333 0.60416666666667 0
0.50000000000000 0.37500000000000 0.62500000000000 0
0.50000000000000 0.35416666666667 0.64583333333333 0
0.50000000000000 0.33333333333333 0.66666666666667 0
0.50000000000000 0.31250000000000 0.68750000000000 0
0.50000000000000 0.29166666666667 0.70833333333333 0
0.50000000000000 0.27083333333333 0.72916666666667 0
0.50000000000000 0.25000000000000 0.75000000000000 0
0.50000000000000 0.25000000000000 0.75000000000000 0
0.50000000000000 0.21875000000000 0.71875000000000 0
0.50000000000000 0.18750000000000 0.68750000000000 0
0.50000000000000 0.15625000000000 0.65625000000000 0
0.50000000000000 0.12500000000000 0.62500000000000 0
0.50000000000000 0.09375000000000 0.59375000000000 0
0.50000000000000 0.06250000000000 0.56250000000000 0
0.50000000000000 0.03125000000000 0.53125000000000 0
0.50000000000000 0.00000000000000 0.50000000000000 0
ポトカー
このシステムは、元素の擬似ポテンシャルの組み合わせに対応しており、ここでは Si の擬似ポテンシャルです。
ステップの実行
それでは、チュートリアルの実践的な部分に移りましょう。チュートリアルでは必要なパッケージを準備しているので、コンテナを直接クローンすることができます。 このチュートリアルでは、RTX 4090 コンピューティング リソース、vasp 6.3.0-cuda11.8 バージョン イメージを使用し、ワークスペースで操作します。
1. コンテナのクローンを作成して起動します
1.1 コンテナが読み込まれるのを待ってから「ワークスペースを開く」をクリックします。
1.2 ターミナルを開く
1.3 wflディレクトリに入る
cd tutorials/wfl
1.4 準備したシリコン擬ポテンシャルをwflディレクトリにアップロードする
ここで使える公式サイトサンプルファイル擬ポテンシャル POTCAR
2. VASPを実行する
mpirun -n 1 vasp_std
3. vaspkitをインストールする
前のディレクトリに戻る
cd ..
3.1 Pythonの依存関係をインストールする
pip install numpy scipy matplotlib
3.2 vaspkit を設定する
chmod 777 setupvk.sh
./setupvk.sh
source ~/.bashrc
cd tutorials
4. vaspkit を使用したデータの処理
4.1 状態密度とバンド図のプロット
次のように入力して wfl ディレクトリに入ります。
cd wfl
状態密度データを生成するには、次のコマンドを入力します。
vaspkit
111
1
vaspkit を使用してバンド データを処理し、プロットするには、次のコマンドを入力します。
vaspkit
252
2
状態密度とバンド図を生成できます。
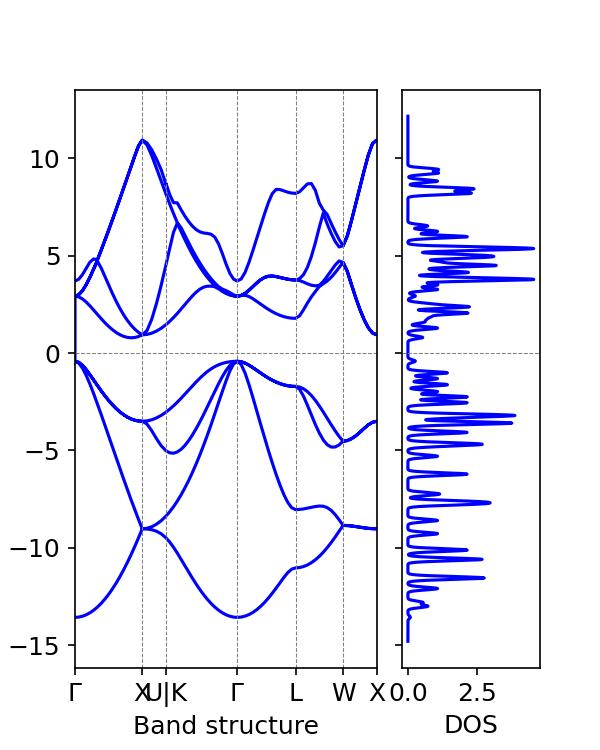
vaspkit を使用してバンドギャップを表示してみましょう。
vaspkit
911
推定されたシリコンバンドギャップは 1.2eV であり、これは典型的なシリコンバンドギャップの実験値 1.12eV に近いことがわかります。
前回のチュートリアルでは、vaspkit を使用した DFT 計算により、バンドギャップが 0.6133 eV であることが明らかになりましたが、これは実験値とは大きく異なります。
したがって、ハイブリッド関数は材料のバンドギャップをより正確に計算できますが、より多くの計算リソースが必要になります。