ニューラル ネットワークの基礎: バックプロパゲーション アルゴリズム

ジェフリー・ヒントン

ジェフリー・ヒントンは、イギリス生まれのカナダのコンピューター科学者および心理学者であり、ニューラル ネットワークの分野で多大な貢献をしており、バックプロパゲーション アルゴリズムの発明者の 1 人であり、深層学習の積極的な推進者として知られています。ニューラルネットワークとディープラーニングの研究。

さらに、ヒントンはロンドン大学の計算神経科学ギャツビーセンターの創設者であり、現在はカナダのトロント大学のコンピューターサイエンス学科の教授を務めています。彼の主な研究方向は、機械学習、記憶、知覚、記号処理の分野における人工ニューラル ネットワークの応用です。現在、ヒントンはニューラル ネットワークを教師なし学習アルゴリズムに適用する方法を研究しています。

ただし、ヒントンの多くの科学研究成果の中で、バックプロパゲーションが最も有名であり、勾配降下法に基づく最新の教師あり学習ニューラル ネットワーク アルゴリズムの基礎でもあります。その主な動作原理は次のとおりです。

実際の演算プロセスでは、ANN アルゴリズムは通常、入力層、隠れ層、出力層の 3 つのカテゴリに分けられます。アルゴリズムの出力結果とターゲット結果の間に誤差がある場合、アルゴリズムは誤差値を計算します。逆伝播を通じてエラー値をアルゴリズムにフィードバックし、関連するパラメーターを変更して調整し、期待と一致する結果が得られるまでこのステップを繰り返します。

バックプロパゲーションを通じて、ANN アルゴリズムはターゲットに近い結果を導き出すことができます。ただし、バックプロパゲーションが ANN アルゴリズムにどのように適用されるかを理解する前に、まず ANN がどのように機能するかを理解する必要があります。

ANN は、人間の脳のニューラル ネットワークに基づく数学モデルまたは計算モデルであり、相互に接続された多数のノード (生物学的ニューロンとして理解できます) で構成されます。

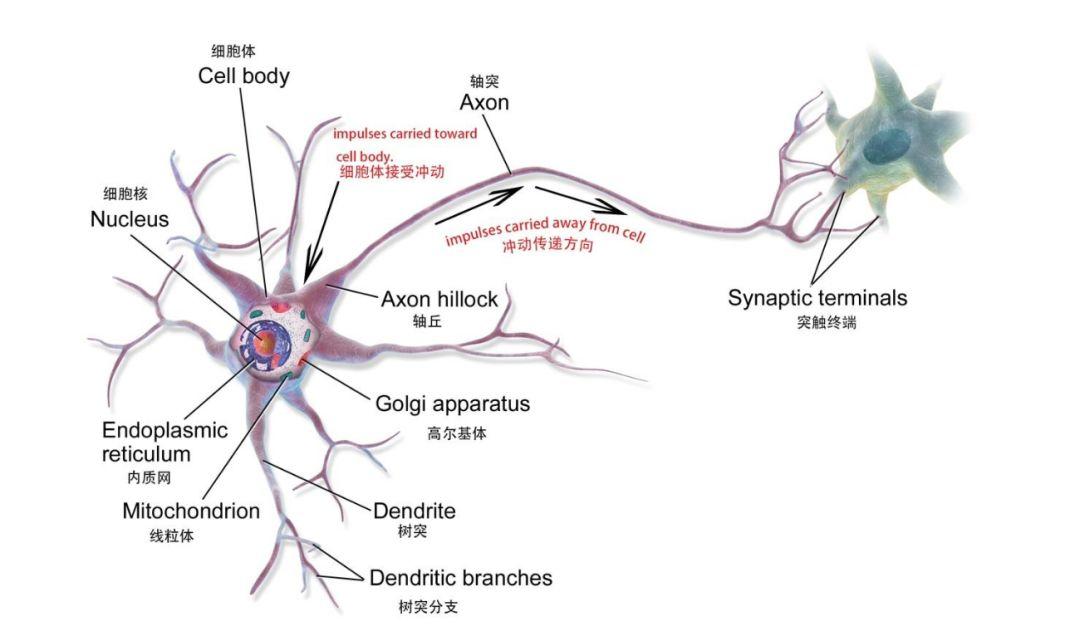
生物学的ニューロン

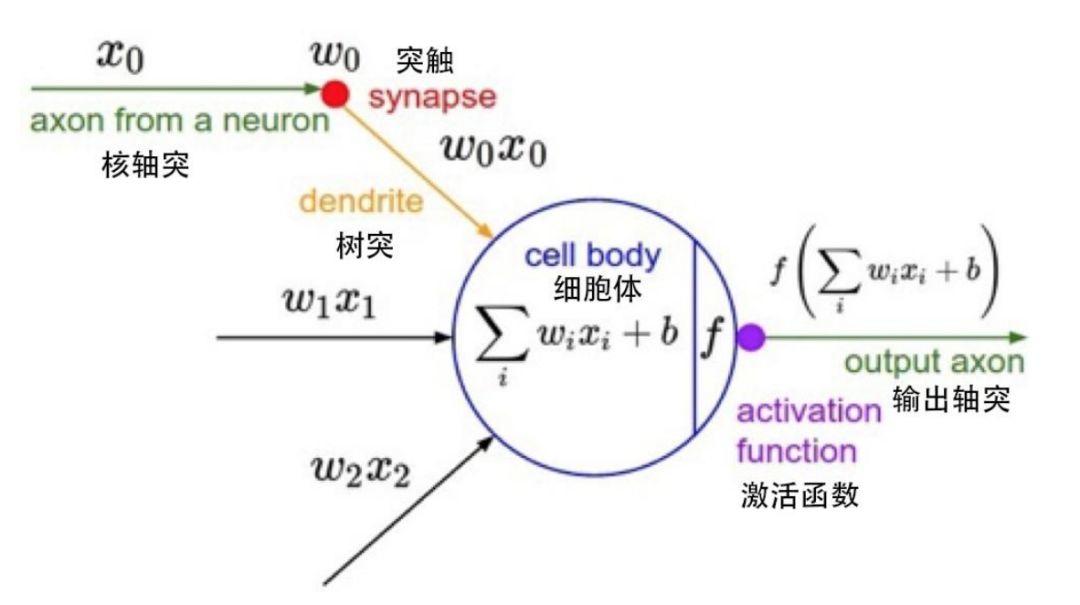
数学モデル内の単一ノード

各ノードは、アクティベーション関数と呼ばれる特定の出力関数を表します。2 つのノード間の接続は、重み値とも呼ばれる重み付けされた値を表します。 ANN アルゴリズムの動作中、各接続は重み w とオフセット b (ANN パラメータとも呼ばれます) に対応します。出力値はノード、ウェイト値、オフセットに関連付けられます。

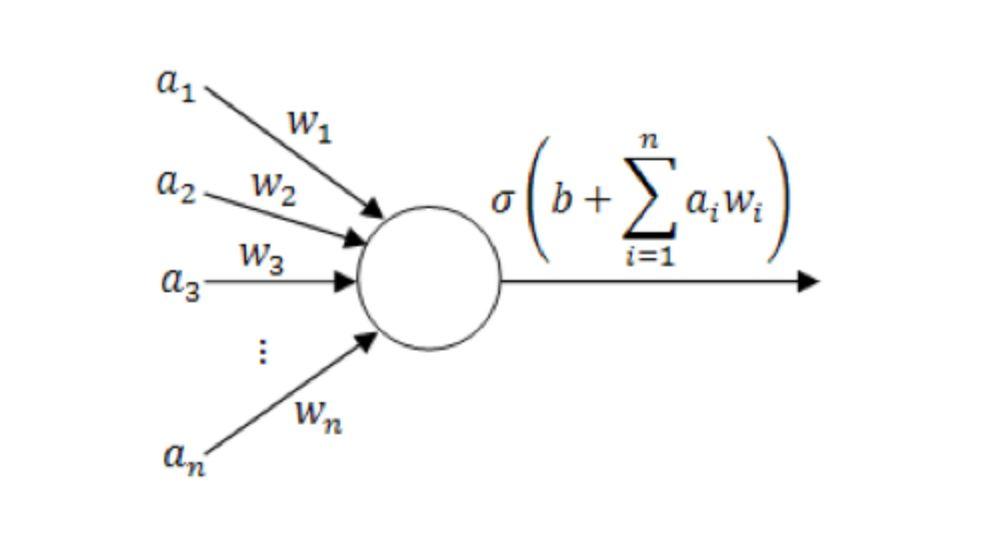
単一ニューロンのモデル図

(ここで、1~an は入力ベクトルの各成分です。1~wn は重み値、b はオフセット、σ は Tanh、Sigmoid、ReLU などの励起関数です)。

完全な ANN には通常、入力層、複数の隠れ層、および出力層が含まれます。隠れ層は主にニューロンで構成され、実際の操作中に最も重要な計算作業を担当します。各層のニューロンは決定を行い、最終結果が出力されるまでその決定を次の隠れ層のニューロンに送信します。 。

したがって、隠れ層が多いほど、ANN はより複雑になり、結果はより正確になります。たとえば、入力された動物が「猫である」か「猫ではない」かを判断するためにANNを使用したい場合、この動物を入力すると、各隠れ層のニューロンがそれを判断し、結果を取得します。そして、結果は、ニューロンの最後の層が結果を出力するまで下方に送信されます。

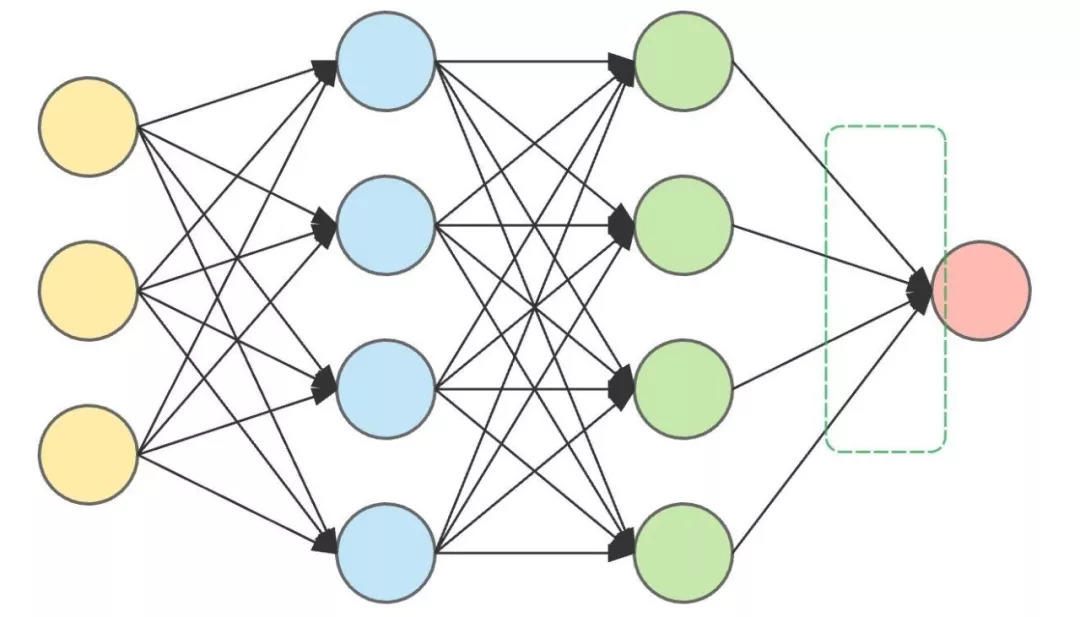
これは 2 つの隠れ層を持つ ANN アーキテクチャです。

両側は入力層 (左) と出力層 (右) で、中央は 2 つの隠れ層です。

動物が生物学的には猫であるにもかかわらず、ANN が「猫ではない」と判断した場合、ANN の出力は正しくありません。ここでできることは、隠れ層に戻って重み値とオフセットを調整することだけです。このデータを返して調整するプロセスがバックプロパゲーションです。

ただし、バックプロパゲーションを実現するには、重要な種類のアルゴリズムにも依存する必要があります。勾配降下アルゴリズムは、学習プロセスを大幅に高速化します。これは、単純に「山の頂上から下るときにピックする」と理解できます。最も急な勾配のある道。

パラメーターを変更するには、出力と実際の値の間の偏差を常に計算する必要があるため (差が大きいほど、変更の規模も大きくなります)、エラー関数 (エラー関数、エラー関数とも呼ばれます) を使用する必要があります。損失関数、損失関数) を使用して、トレーニング セット内のすべてのサンプルの最終結果を測定します。予測値と実際の値の間の誤差。

で やあ は予測結果、y私 実際の結果については。

この式は、最終的な予測値とトレーニング セット内のすべてのサンプルの実際の値の間の誤差を測定します。これは出力層の予測カテゴリにのみ関連しますが、この予測値は前の層のパラメーターに依存します。犬を猫と考えたくない場合は、この誤差関数を最小限に抑える必要があります。

勾配降下法アルゴリズムは、誤差関数を最小化するアルゴリズムの 1 つであり、ANN モデルのトレーニングで一般的に使用される最適化アルゴリズムでもあります。関数パラメーターのセットが与えられると、勾配降下法はパラメーター値の初期セットから開始され、損失関数を最小化するパラメーター値のセットに向かって反復的に移動します。この反復最小化は、勾配の負の方向の勾配変化を考慮した微積分を使用して実装されます。勾配降下法を使用する典型的な例は線形回帰です。モデルが反復されると、損失関数は徐々に最小値に収束します。

勾配は偏導関数を計算して得られる、ある点における関数の変化率が最も大きくなる方向を表すため、勾配降下法を用いることで学習処理が大幅に高速化されます。

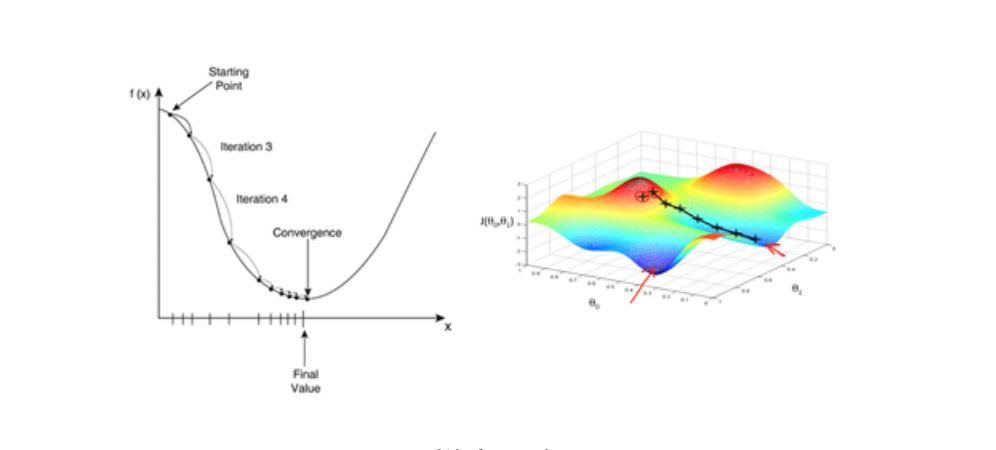
勾配降下法

実際には、理論的には、最初に最後のレイヤーの重み値とオフセットが結果にどのような影響を与えるかを確認することが可能です。誤差関数 E の偏微分を取ることにより、誤差関数に対する重み値とオフセットの影響を確認できます。

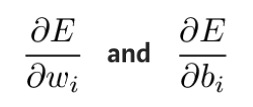
これらの偏導関数は、連鎖導出ルールを通じて計算して、これらのパラメーターの変更が出力に及ぼす影響を取得できます。導出式は次のとおりです。

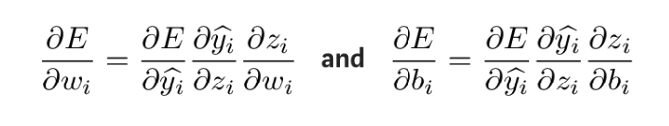
上の式で未知の量を取得するには、wi と bi についてそれぞれ zi の偏微分を求めます。

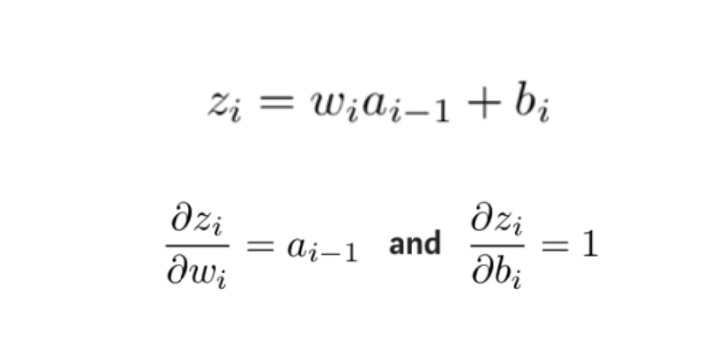次に、各層の重み値とオフセットに対する誤差関数の偏導関数が逆算され、調整された重み値とオフセットが、誤差のある最初の層まで勾配降下法によって更新されます。

このプロセスは、BP アルゴリズムとしても知られる逆伝播アルゴリズムであり、出力層の誤差を層ごとに逆方向に伝播し、偏導関数を計算してネットワーク パラメータを更新して誤差関数を最小化します。アルゴリズムにより期待される出力が得られます。

現在、バックプロパゲーションは主に教師あり学習下の ANN アルゴリズムで使用されています。