物質探求の新時代!清華大学の Xu Yong と Duan Wenhui のチームは、ニューラル ネットワーク密度関数フレームワークをリリースし、物質の電子構造を予測するためのブラック ボックスを開きました。

密度汎関数理論 (DFT) は、材料特性を予測および説明するための重要なツールとして、物理学、化学、材料科学およびその他の分野で不可欠な役割を果たしています。ただし、従来の DFT は通常、多くのコンピューティング リソースと時間を消費し、その適用範囲は大幅に制限されています。

新たな学際分野として、深層学習と密度汎関数理論を組み合わせて、多数の計算シミュレーションを通じて新しい材料を予測および発見することで、計算材料データベースの構築における従来の DFT 計算の時間のかかる複雑な欠点が徐々に克服されつつあります。応用の可能性。ニューラル ネットワーク アルゴリズムは、大規模な材料データベースの構築を加速し、より大きなデータ セットでより強力なニューラル ネットワーク モデルをトレーニングできます。ただし、現在の深層学習 DFT 研究のほとんどは DFT タスクとニューラル ネットワークを別々に扱っているため、両者間の共同開発が大幅に制限されています。

ニューラル ネットワーク アルゴリズムと DFT アルゴリズムをより有機的に組み合わせるために、清華大学の Xu Yong と Duan Wenhui の研究グループは、ニューラル ネットワーク密度汎関数理論 (ニューラル ネットワーク DFT) フレームワークを提案しました。このフレームワークは、ニューラル ネットワークの損失関数の最小化と密度汎関数理論のエネルギー関数の最適化を統合し、従来の教師あり学習手法と比較して精度と効率が高く、深層学習 DFT 手法の開発に新たな道を開きます。新しい方法。

この研究は「変分エネルギー最小化に基づくニューラルネットワーク密度汎関数理論」と題され、Phys Rev. Lett.

研究のハイライト:

* この研究は、変分密度汎関数理論と等価ニューラル ネットワークを組み合わせたニューラル ネットワーク密度汎関数理論の理論的枠組みを提案します。

※本研究はJulia言語をベースにZygote自動微分フレームワークを組み合わせ、AI2DFTという計算プログラムをスクラッチから開発しました。 AI2DFT では、変分 DFT 計算とニューラル ネットワーク トレーニングの両方に自動微分 (AD) を使用できます。

用紙のアドレス:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.076401

オープンソース プロジェクト「awesome-ai4s」は、100 を超える AI4S 論文の解釈をまとめ、大規模なデータ セットとツールを提供します。

https://github.com/hyperai/awesome-ai4s

深層学習と DFT を統合して、物理情報の教師なし学習を実現します

Kohn-Sham DFT は、材料シミュレーションで最も広く使用されている第一原理計算 (ab initio 計算) 手法です。この方法は、複雑な電子相互作用問題を単純化し、有効な単一粒子コーン・シャム ハミルトニアンによって記述される単純化された非相互作用電子問題にマッピングし、近似交換相関関数を使用して複雑な多体効果を考慮します。コーン・シャム方程式は変分原理から正式に導出され、理論物理学の分野で非常に人気がありますが、微分方程式の反復解法がより効率的であるため、この方法は DFT 計算では一般的に使用されません。

しかし、ディープラーニングと DFT のさらなる統合により、この開発パラダイムは完全に変わりました。

深層学習 DFT の研究は主にデータ駆動型教師あり学習技術に依存しています。以下の図 a に示すように、一般に、従来のデータ駆動型教師あり学習手法は、さまざまな材料構造に対して DFT SCF 計算を実行することでトレーニング データを生成し、DFT 結果と同様のデータを予測するニューラル ネットワークを設計およびトレーニングします。このプロセスでは、ニューラル ネットワークと DFT が分離されます。

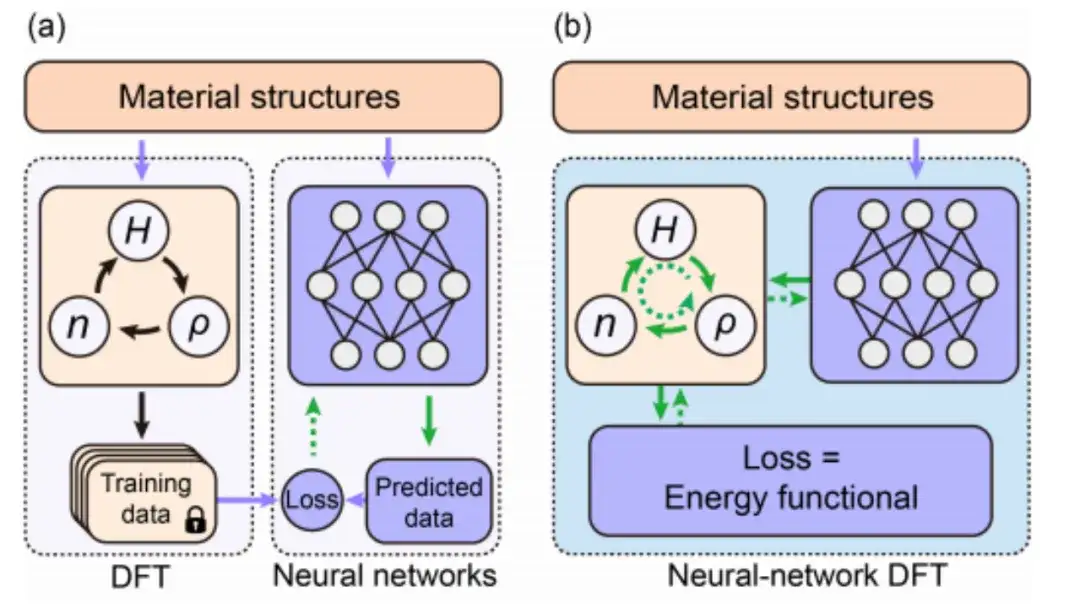
現在、上の図 b に示すように、ニューラル ネットワーク DFT に基づく物理情報の教師なし学習では、DFT のエネルギー関数の最適化とニューラル ネットワークの損失関数の最小化が組み合わされて、ニューラル ネットワーク アルゴリズムと DFT アルゴリズムの統合が実現されています。共有とコラボレーション。さらに重要なことは、深層学習に DFT を明示的に導入することにより、ニューラル ネットワーク モデルは、以前のデータ トレーニング方法よりも実際の物理環境をより適切にシミュレートできるようになります。

ニューラルネットワークDFTを数値的に実装するための自動微分や逆伝播などの技術の導入

この研究では、その後の研究のためにエネルギー汎関数 E[H] を選択し、3 次元ユークリッド群のマッピング {R} → H の共分散を保証するために DeepH-E3 を採用しました。

* DeepH-E3、同等のニューラル ネットワークに基づいて Xu Yong のチームによって設計された第 2 世代 DeepH アーキテクチャ。このフレームワークは、3 次元ユークリッド群の下で共変ニューラル ネットワークを使用して、微視的な原子構造に対応する密度汎関数理論 (DFT) ハミルトニアンを予測します。これにより、第一原理電子構造計算が大幅に高速化されます。

具体的には、下図に示すように、本研究では等変ニューラルネットワークの入力条件として材料構造情報の埋め込みを使用し、ハミルトニアン行列を出力してニューラルネットワークの重みパラメータ化のHθとエネルギー汎関数Eを取得します。 [H] はニューラルネットワークの損失関数 E[Hθ] とみなすこともできます。

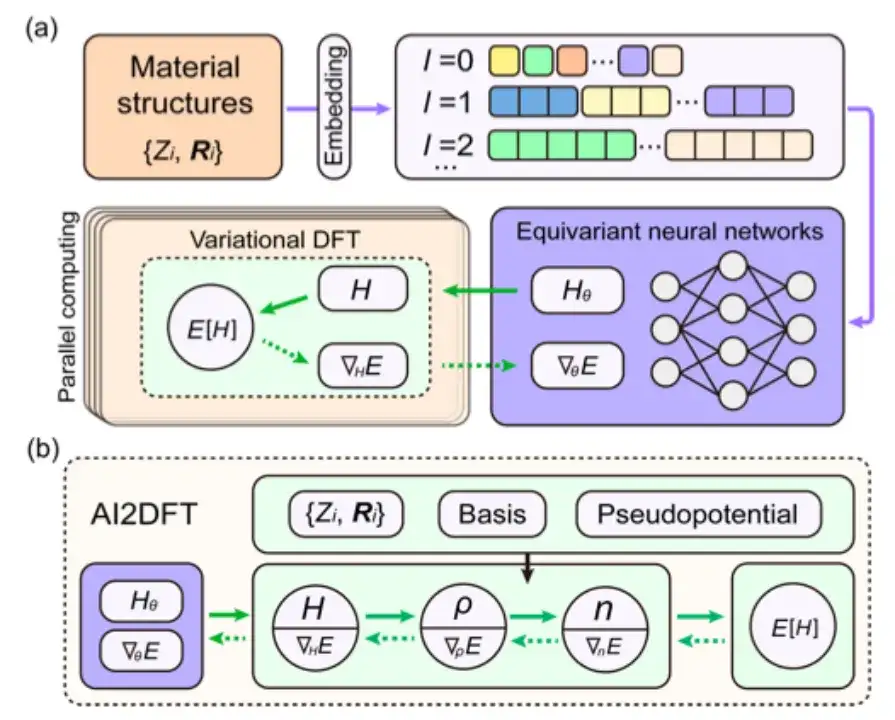
ニューラル ネットワーク DFT では、DFT プログラムはニューラル ネットワーク パラメーターを最適化するために ∇HE を提供する必要があります。これは、DFT プログラミングにとって大きな課題です。

自動微分 (AD) は ∇HE の計算に適していますが、現在のほとんどの DFT コードは AD 機能を完全にはサポートしていません。そこで本研究では、Julia言語を用いた自律的かつ利用可能な自動微分可能DFTプログラム「AI2DFT」を開発した。 AI2DFT では、自動微分 (AD) が DFT 計算とニューラル ネットワーク トレーニングの両方に適していることに注目してください。

DFT では、AI2DFT は H を通じて ρ と n を導出して総エネルギーを計算し、リバース モード AD を使用して連鎖規則に基づいて ∇nE、∇ρE、および ∇HE を順番に計算します。ニューラル ネットワークでは、勾配情報 ∇θE をニューラル ネットワークの最適化に使用できます。

研究結果：ニューラルネットワークDFTは信頼性が高く、予測精度に優れる

ニューラル ネットワーク DFT の理論的枠組みを確立し、微分可能でプログラム可能な AI2DFT コードによる数値実装を完了した後、この研究では、H2O 分子、グラフェン、単層 MoS2、体心立方体 Na テストを含む一連の材料について包括的な実験を実施しました。

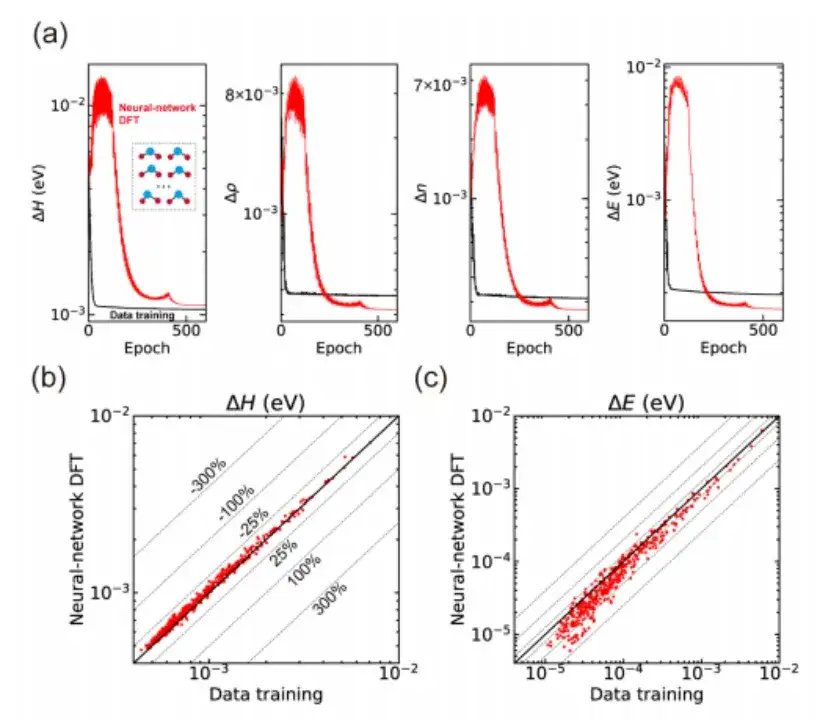
具体的には、この研究ではまず、AI2DFT の SCF 反復が SIESTA コードのベンチマーク結果をうまく再現できるかどうかを調べ、次に同じ材料に変分 DFT を適用します。以下の図 a と b に示すように、数十の変動ステップの後、総エネルギーは μeV スケール未満に収束する可能性があり、エネルギー勾配、ハミルトニアン、密度行列、電荷密度などの他の物理量も指数関数的な収束を示し、信頼性と信頼性が検証されます。変分DFTのロバスト性。

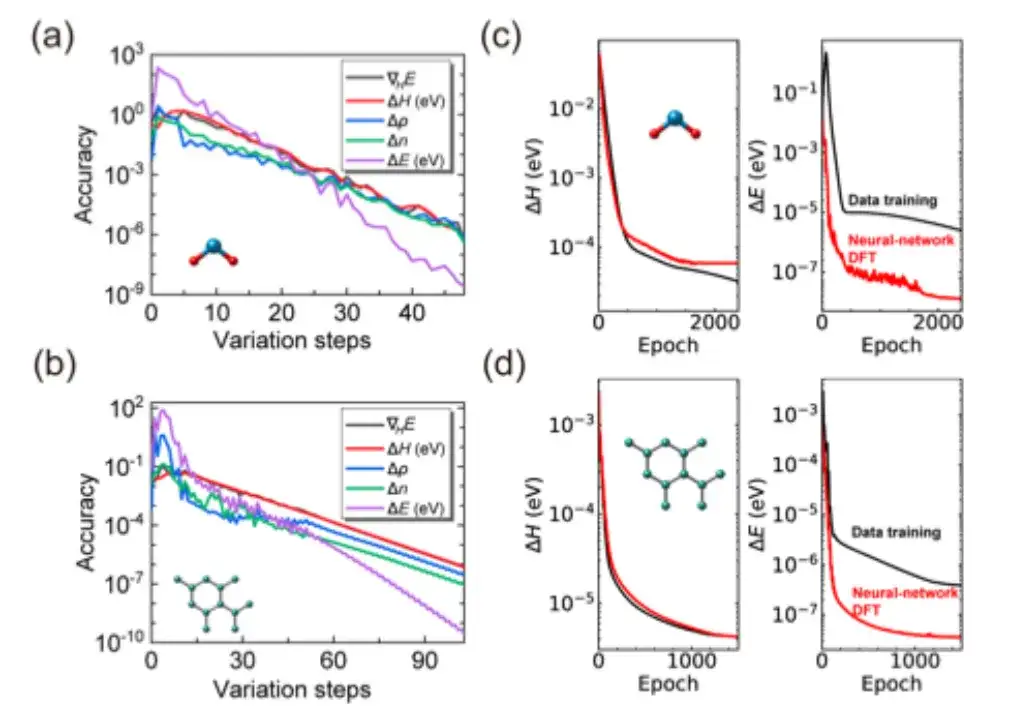
それだけでなく、上の図 c と d に示すように、従来のデータ駆動型教師あり学習方法と比較して、AI2DFT は変分 DFT と DeepH-E3 ニューラル ネットワークのパフォーマンスを組み合わせています。例えば：

* H2O 分子の場合、DFT ハミルトニアンはニューラル ネットワーク DFT を通じて最適化され、高精度を実現できます。ニューラル ネットワーク DFT の精度は 0.06 meV、データ トレーニングの精度は 0.02 meV です。

* グラフェンの場合、両方の方法で 0.004 meV というより高い精度が達成されました。したがって、ニューラルネットワーク手法の信頼性が検証される。

* さらに、エネルギー予測精度の点では、ニューラル ネットワーク DFT のパフォーマンスはデータ トレーニングよりも大幅に優れています。たとえば、H2O 分子の場合、ニューラル ネットワーク DFT のエネルギー予測精度は 0.013 μeV に達し、データ トレーニングの 0.83 μeV よりも 60 倍以上高くなっています。

最後に、この研究ではニューラル ネットワーク DFT をさまざまな材料構造計算に適用し、教師なし学習の能力も実証しました。H2O 分子を例にとると、以下の図 a に示すように、この研究ではまず DeepH-E3 手法に基づくデータ駆動型教師あり学習を通じて事前トレーニング済みニューラル ネットワーク モデルを取得し、次にニューラル ネットワーク DFT を使用して微調整しました。ハミルトニアンやその他の物理量の高精度予測を実現する 300 のトレーニング構造。

それだけでなく、この研究では、トレーニングされたニューラル ネットワーク モデルを使用して、トレーニング プロセス中には見られなかった 435 個のテスト構造を予測しました。その結果は、上の図 b と c に示すように、優れた一般化能力も示しました。データ駆動型教師あり学習と比較して、ニューラル ネットワーク DFT によって生成されたハミルトニアンは、平均絶対誤差がわずかに大きいものの、予測精度の点で優れたパフォーマンスを示します。これは、ニューラル ネットワークがニューラル ネットワーク DFT プロセスを通じて学習されたことを意味します。物理モード。

DFT と第一原理計算に焦点を当て、AI が材料科学の新時代をリード

清華大学のXu Yong教授とDuan Wenhui教授が率いる研究チームは、Li Yang氏、Tang Zechen氏、Chen Zezhou氏らが結集し、密度汎関数理論（DFT）と第一原理計算で一連の成果を達成した。材料科学と物理学の研究におけるテクノロジーの幅広い応用について学びます。

2022 年以来、Xu Yong と Duan Wenhui の研究チームは、第一原理コンピューティングの分野で大きな進歩を遂げてきました。彼らは、深層学習 - DeepH (Deep DFT Hamiltonian) に基づいた理論的フレームワークとアルゴリズムを開発しました。この手法は、電子物性の局所原理を最大限に活用し、小規模なシステム データセットでトレーニングされたモデルを使用するだけで、大規模な材料系を正確に予測できるため、非磁性体の電子構造の計算効率が大幅に向上します。材料。

関連する結果は、「効率的な非経験的電子構造計算のための深層学習密度汎関数理論ハミルトニアン」というタイトルで Nature Computational Science に掲載されました。
論文リンク:
https://www.nature.com/articles/s43588-022-00265-6

2023 年、磁性材料の DFT ハミルトニアンの原子と磁気構造への依存性をさらに研究するために、Xu Yong と Duan Wenhui の研究チームは xDeepH (拡張 DeepH) メソッドを提案しました。この方法では、ディープ等変ニューラル ネットワーク フレームワークを使用して磁性材料の DFT ハミルトニアンを表現し、効率的な電子構造計算を実行します。この成果は、磁気構造の研究のための効率的かつ正確な計算ツールを提供するだけでなく、DFT の精度と効率のバランスをとるための実現可能な方法も提案します。

関連する結果は、「磁気超構造の深層学習電子構造計算」というタイトルで Nature Computational Science に掲載されました。
論文リンク:
https://www.nature.com/articles/s43588-023-00424-3

事前知識と対称性要件を含むニューラル ネットワーク モデルを設計するために、研究者らはさらに DeepH-E3 手法を提案しました。この方法では、少量の DFT データを使用して小規模システムをトレーニングし、大規模な材料システムの電子構造を迅速に予測できます。計算速度が数桁大幅に向上するだけでなく、予測精度もサブミリ電子ボルトの高水準に達します。

関連する結果は、「密度汎関数理論ハミルトニアンの E(3) 等変ニューラル ネットワーク表現の一般的なフレームワーク」というタイトルで Nature Communications に掲載されました。
論文リンク:
https://www.nature.com/articles/s41467-023-38468-8

DeepHは、理論枠組みの継続的な最適化により、非磁性材料から磁性材料までの包括的なカバーを実現し、予測精度も大幅に向上しました。このような背景に対して、Xu Yong と Duan Wenhui の研究チームは、DeepH 手法をさらに使用して、DeepH ユニバーサル材料モデルを構築しました。このモデルは、複数の元素と複雑な原子構造を含む材料系を処理することができ、材料特性の予測において優れた精度を示します。

関連する研究結果は、「深層学習密度汎関数理論ハミルトニアンの普遍的材料モデル」というタイトルで Science Bulletin に掲載されました。
論文リンク:
https://doi.org/10.1016/j.scib.2024.06.011

今回、Xu Yong 氏と Duan Wenhui 氏の研究グループは、ニューラル ネットワーク アルゴリズムと DFT アルゴリズムを有機的に組み合わせ、ディープラーニング DFT 手法を開発する新しい方法を切り開きました。ディープ ニューラル ネットワーク アルゴリズムが進歩し続け、より大規模なデータ セットが作成されるにつれて、AI がより賢くなることは疑いの余地がありません。近い将来、第一原理コンピューティング、材料発見、設計はすべて AI によって強化される可能性があります。ニューラル ネットワークが終了します。これは、AI が材料科学を新たなデータ主導の時代に導くことを示しています。