中国科学院半導体研究所の論文が再び TNNLS のトップ号に掲載され、数式の探究に新たな視点をもたらしました

数式を解くことは機械学習の分野で非常に重要な研究テーマであり、シンボリック回帰 (SR) はデータから正確な数式を見つける方法です。

シンボリック回帰は、特定の観測データの潜在的な数式を明らかにするために使用され、変数間の因果関係を説明したり、複雑なシステムの発展傾向を予測したりすることができます。そして天文学の応用。

有名な応用例は、ケプラーの惑星軌道の発見です。科学者は記号回帰アルゴリズムを使用して、天体の運動に関する新しい法則を発見し、それによってその軌道を推定しました。これは人類による宇宙の星と海の探査に対する重要な貢献です。

ただし、記号回帰研究には独自の困難もあります。シンボリック回帰は、独立変数 X と従属変数 Y を考慮してこれらの要素の最適な組み合わせを取得し、最適な係数を求めることに重点を置いています。ただし、最適な組み合わせを取得することは NP 困難問題 (非決定的多項式) であり、組み合わせ空間はシンボリック式の長さに応じて指数関数的に増大します。また、係数の非線形解法処理と要素の組み合わせの最適化処理が相互に干渉するため、正確な式を決定するのに非常に時間がかかります。

この難しい学術問題に応えて、中国科学院半導体研究所の研究者は、式構造の解決を分類問題とみなして教師あり学習を通じて解決し、記号式を表現するために DeepSymNet と呼ばれる記号ネットワークを提案しました。教師あり学習に基づく現在一般的な SR アルゴリズムのいくつかと比較して、DeepSymNet は短いラベルを使用するため、予測のための検索スペースが削減され、アルゴリズムの堅牢性が向上します。

用紙のアドレス:
https://ieeexplore.ieee.org/document/10327762
公式アカウントをフォローし、バックグラウンドで「DeepSymNet」と返信すると論文をダウンロードできます

既存の手法の限界が浮き彫りになる

現在、一般的なシンボリック式構造を解決するには、主に 2 つの方法があります。

• 検索ベースのソリューション

古典的な検索ベースのソリューションは GP (遺伝的プログラミング) アルゴリズムです。まず、初期集団として多くの式がランダムに取得され、複製、交換、突然変異を通じて進化し、より小さい善性を持つ子孫を選択して、その式が善性の要件を満たすまで進化を続けます。

さらに、検索ベースの手法の中には、シンボル ツリーをシーケンスとしてエンコードし、深層強化学習でポリシー勾配法を使用する DSR アルゴリズムなど、強化学習を使用して適切な表現構造を検索する重要なクラスの手法があります。解決する。 DSR の背後にある考え方は、より大きな報酬を持つ式のサンプリング確率を高め、それによってより小さな誤差を持つ式を生成することです。

物理式用の SR アルゴリズムもあります - AIFeynman は、主に物理学の事前知識を使用して式の構造を決定し、それによって式をより小さなサブ問題に分解し、探索空間を削減します。もう 1 つはスパース最適化手法に基づいています。 EQL は主に、スパース最適化と組み合わせた BP アルゴリズムを使用してパラメーターを学習し、それによって EQL ネットワーク内のスパース サブネットワークを取得し、数式構造を取得します。

このタイプの方法には、明らかな欠点に加えて、検索スペースが大きく、ソリューション エクスペリエンスを再利用できないため、処理が遅いという共通の欠点があります。

• 教師あり学習に基づくソリューション

教師あり学習に基づくソリューションは、時間のかかる検索ベースのソリューションの欠点を克服できます。代表的な手法には、SymbolicGPT、NeSymReS、E2E があります。

* SymbolicGPT は、シンボリック式を文字列にエンコードし、式構造のソリューションを言語翻訳タスクとして扱います。その言語翻訳プロセスでは、教師ありトレーニング用に人工的に生成された多数のサンプルが使用されます。

* NeSymReS は、事前順序トラバーサルを通じてシンボル ツリーをシーケンスとしてエンコードし、トレーニングに set Transformer を使用します。

* E2E は、式の構造と係数をトレーニング用のラベルにエンコードすることで、式の構造と係数を同時に予測します。

ただし、これらのソリューションには、複数の等価ラベルと不均衡なトレーニング サンプルの問題があり、トレーニング プロセス中に曖昧さが生じやすく、アルゴリズムの堅牢性に影響を与えます。さらに、SymbolicGPT には、サンプリングに使用されるシンボルの数が最大でも 4 つのレイヤーしかないため、考慮される式が比較的単純であるため、E2E は係数をラベルにエンコードし、ラベルが非常に長くなり、予測に影響を与えるなど、他の欠点もあります。精度など

問題を解決する新しい方法—DeepSymNet

中国科学院半導体研究所の研究者らは、記号表現を表現するために DeepSymNet と呼ばれる新しい記号ネットワークを提案し、DeepSymNet の全体的なフレームワークを実証しました。最初の層はデータ、中間層は隠れ層、最後の層は出力層です。

隠れ層ノードは、+、-、×、÷、sin、cos、exp、log、id などの演算記号で構成されます。id 演算子は EQL の id 演算子と同じです。

各隠れ層の id 演算子の数は前の層のノードの数と等しくなりますが、他の演算子は各隠れ層に 1 回だけ現れます。オペレータIDは前層のノードと1対1に対応しており、その機能により各層は前層の情報を全て利用することができる。他の演算子は通常の演算子であり、前の層に完全に接続されています。

id 演算子と前の層との接続は固定されており、通常の演算子は前の層との接続がないか、1 つまたは 2 つの接続があります。これは、このネットワークではサブネットワークがシンボリック式を表すことを意味します。式が占める隠れ層が多いほど、その複雑さは高くなります。そのため、隠れ層の数は式の複雑さの大まかな尺度として使用できます。

ただし、入力層には特別なノード「const」があり、シンボリック式で定数係数を表すために使用されることに注意してください。 「const」ノードに接続されたエッジのみが重み (定数係数) を持ち、シンボリック式に十分な定数係数が出現するのを防ぎます。

全体として、DeepSymNet は、あらゆる式を表現できる完全なネットワークです。SR のソリューションは、DeepSymNet 内のサブネットワークを検索するプロセスです。

2 組の実験比較により利点が示される

研究チームは人工的に生成されたデータセットと公開データセットに基づいてテストを実施し、現在普及しているアルゴリズムを比較しました。

データセットのダウンロードアドレス:
https://hyper.ai/datasets/29321

実験では、DeepSymNet には最大 6 つの隠れ層があり、最大 3 つの変数をサポートします。研究チームは、ラベルごとに 20 個のサンプルを生成し、それぞれに 20 個のデータ ポイントが含まれています。定数係数と変数の両方のサンプリング間隔は [-2,2] です。トレーニング戦略は、早期に停止することです (つまり、検証セットの損失が減少しなくなったときにトレーニングを停止します)。 Adam オプティマイザーによって支援されます。

• 人工的に生成されたデータのテスト結果

テスト結果は次のことを示しています。

* 予測オブジェクトの数が増えると予測の難易度が上がり、式の隠れ層 (つまり、複雑さ) も増加します。

* ラベル予測のボトルネックは演算子の選択にあります。

* DSN2 は DSN1 よりも適切に最適解と近似解を解きます。

* 同等のラベルのマージとサンプルのバランスにより、アルゴリズムの堅牢性が強化されます。

初め、DeepSymNet は、シンボル ツリーよりも効率的に式を表現できます。式内に複数回出現する同じモジュールの場合、DeepSymNet の平均ラベル長は NeSymRes よりも短くなります。

上の図に示すように、DeepSymNet ラベルを使用してトレーニングされたモデルの予測精度は、NeSymReS ラベルを使用してトレーニングされたモデルの予測精度をはるかに上回ります。これは、DeepSymNet ラベルがシンボル ツリー ラベルよりも優れていることを示しています。

第二に、式が占める隠れ層の数が増加するにつれて、モデルの予測精度は急速に低下します。そこで研究チームは、ラベル予測の問題をより適切に解決できるように、ラベル予測を演算子予測と接続関係予測の2つのサブタスクに分割できることを提案しました。

DeepSymNet を 2 つの部分に分割して学習した結果、隠れ層の数が増加するにつれて、接続関係の予測精度は高いままであるものの、演算子選択の予測精度は急激に低下することがわかりました。これは、演算子の選択空間が接続関係の選択空間よりもはるかに大きいためです。したがって、オペレーターの選択の精度を向上させるために、研究者はオペレーターの選択に関する別のトレーニングを実施しました。

予測プロセス中、チームはまずオペレーター選択モデルを使用してオペレーター選択シーケンスを取得し、それをトレーニング済みモデル DSN1 に入力して接続関係を予測しました。テスト結果は上記のとおりです。オペレーターの選択に関する個別のトレーニングの後、予測精度が大幅に向上しました。個別にトレーニングされたモデルは DSN2 と呼ばれます。

さらに、研究者らは、等価ラベルの結合とサンプルのバランスの堅牢性を検証するためにアブレーション実験も実施しました。まず、128,455 の異なるラベル (TrainDataOrg) を含む 500,000 のトレーニング サンプルがランダムに選択されました。これらのラベルのサンプル数の分布は著しく不均一であることがわかりました。最小サンプル数は 1、最大サンプル数は 13,196、サンプル数の分散は 13,012.29 でした。

次に、チームはサンプル数のバランスをとり、トレーニング サンプル TrainDataB と、同等のラベルを結合して得られたトレーニング サンプル TrainDataBM を取得しました。

続いて、3 つのトレーニング データに基づいてモデル DSNOrg、DSNB、および DSNBM が取得され、これら 3 つのモデルの精度が前から後ろに順に増加しました。これは、サンプル バランスを追加し、同等のラベルを結合した後、最適解を求めるモデルの精度が向上し、実際にアルゴリズムの堅牢性が向上し、アルゴリズムのパフォーマンスが向上したことを示しています。

• 公開データセットのテスト結果

研究チームは 6 つのテスト データ セットを使用しました。コザ 、Korns、Keijzer、Vlad、ODE、および AIFeynman、変数が 3 つ以下の式がテスト用にこれらのデータ セットから選択されました。教師あり学習に基づく現在一般的な手法と比較すると、このアルゴリズム (DSN1、DSN2) の精度が比較アルゴリズムよりも優れていることがわかります。

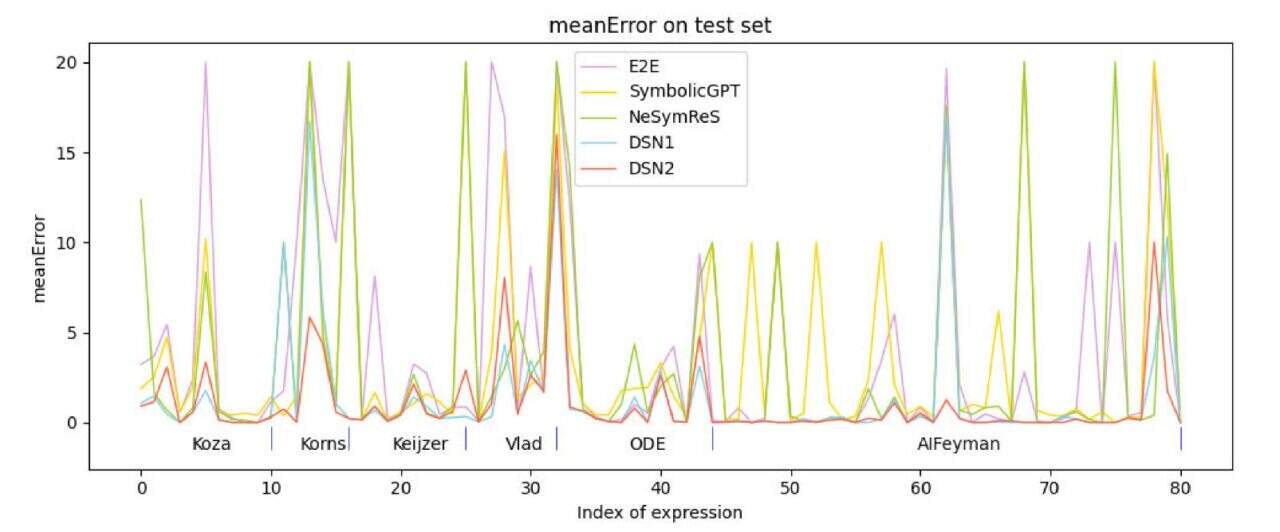
さらに、チームはアルゴリズムを現在人気のある検索ベースの手法である EQL、GP、DSR と比較しました。その結果を下の図に示します。

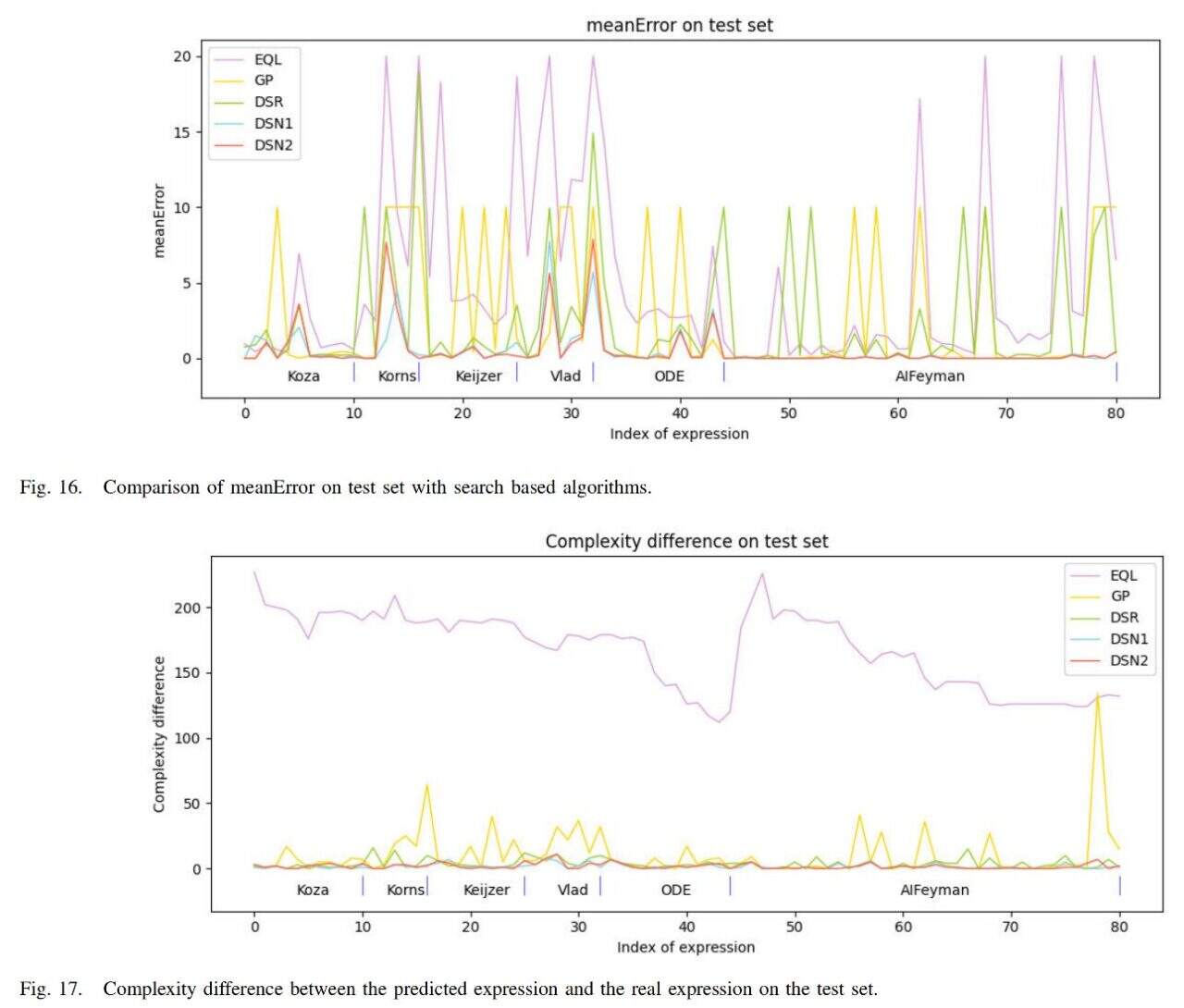
このアルゴリズム (DSN1、DSN2) の平均誤差は最も小さく、得られる式の複雑さも実際の式の複雑さに最も近くなります。

要約すると、結果に基づいて次のように結論付けることができます。研究チームが研究したアルゴリズムは、記号表現のエラー、記号表現の複雑さ、実行速度の3つの側面で比較アルゴリズムよりも優れており、アルゴリズムの有効性が確認された。

背後にあるチームにはスターがちりばめられています

象徴的回帰という中核問題に関しては、世界中の科学者が絶えず熱心に取り組んでいます。論文では DeepSymNet にはまだいくつかの制限があると述べられていますが、この研究は依然として数学的問題を解決する上で人工知能に重要な貢献をしており、完全に教師あり学習に基づいた SR 手法を提供していることは間違いありません。問題を解決する新しい方法。

もちろん、この成果は、論文の筆頭著者であるウー・ミン氏をはじめとする多くの人々の血と汗の賜物であると、中国科学院半導体研究所の公式ウェブサイトによると、Wu Min 氏は現在、中国科学院半導体研究所の助研究員であり、「深層学習に基づくシンボリック回帰と半導体デバイス開発におけるその応用」、「ニューラル ネットワークの分断」などの多くの科学研究プロジェクトに参加しています。 -and-conquer 知識融合のためのリダクションシンボリック回帰法」などのプロジェクト。

加えて、この論文の著者のうち、Liu Jingyi 博士は、昨年 7 月にトップの人工知能ジャーナル Neural Networks に「SNR: Symbolic Network-based Rectifiable Learning Framework for Symbolic Regression」というタイトルの論文を筆頭著者として掲載しました。記号回帰問題には、修正機能を備えた学習フレームワークが提供されます。

関連テーマの研究から判断すると、中国は革新的な手法を着実にリードしており、今後期待されるのは、これらの理論と研究結果が近い将来、実際的な問題の解決に確実に貢献することです。