チューリングがAIの父なら、シャノンはAIの叔父に当たるのではないでしょうか？

シャノンは若い頃からハンサムで自信に満ちており、発明家エジソンの遠い親戚でもありました。

1916年4月30日、クロード・シャノンは米国ミシガン州のゲイロードという小さな町で生まれ、この時チューリングは遠く離れたイギリスにいて4歳に成長していた。シャノンは 1936 年にミシガン大学で数学と電気工学の学士号を取得しました。彼は 1940 年に MIT で数学の修士号と博士号を取得し、1941 年にベル研究所に入社しました。

チューリングに比べて、シャノンの人生は平穏でした。彼は 2001 年 2 月 26 日に 84 歳で亡くなりました。

シャノンによって開拓された情報理論は、情報通信科学の基礎であるだけでなく、今日でも情報通信科学の基礎となっています。これはディープラーニングの重要な理論的基礎です。

情報理論は、微積分、確率論、統計などの多くの分野を包括的に使用し、深層学習でも非常に重要な役割を果たします。

• 一般的なクロスエントロピー損失関数。

• 最大の情報獲得に基づいて決定木を構築します。

• NLP と音声で広く使用されているビタビ アルゴリズム。

• 機械翻訳で一般的に使用される RNN、およびさまざまなタイプのモデルで一般的に使用されるエンコーダーとデコーダー。

簡単な例から紹介しましょう。次の 2 つの文には含まれる情報量が異なります。

「ブルーノは犬です。」

「ブルーノは大きな茶色の犬です。」

明らかに、2 つの文は最初の文と比べて、異なる量の情報を伝えています。この文では、ブルーノが犬であることがわかるだけでなく、犬の毛の色と大きさもわかります。

しかし、これら 2 つの単純な文は、20 世紀初頭の科学者や技術者にとって最大の頭痛の種でした。

彼らは、これらのメッセージ間の違いを定量化し、数学的に説明したいと考えています。

残念ながら、これを行うためのすぐに利用できる分析的または数学的手法はありませんでした。

それ以来、科学者たちはデータの意味論から答えを見つけることを期待して、この質問に対する答えを探し続けてきました。しかし、そのような研究は問題をさらに複雑にするだけであることが判明しました。

数学者でエンジニアのシャノンがこの問題を導入するまで "エントロピ"コンセプトのその後。情報の定量的測定の問題はついに解決され、これは「デジタル情報時代」への突入の始まりでもあります。

シャノンはデータの意味論的な研究にエネルギーを費やさず、確率分布と 「不確実性」情報を数値化して紹介する "少し"情報量を測るという概念。

彼は、情報コンテンツに関しては、データのセマンティクスは重要ではないと信じています。

この革新的なアイデアは、情報理論の基礎を築いただけでなく、人工知能やその他の分野の発展に新たな道を切り開きました。したがって、クロード・シャノンは情報時代の父とも認められています。

情報理論には多くの応用シナリオがあります。ここでは主に、深層学習とデータ サイエンスの分野における 4 つの一般的な応用例を見ていきます。

エントロピ

情報エントロピーまたはシャノン エントロピーとも呼ばれ、不確実な結果を測定するために使用されます。次の 2 つの実験を通じて理解できます。

• 結果の確率が 0.5 になるように公正なコインを投げます。

• 結果の確率が 0.99 になるように偏ったコインを投げます。

明らかに、実験 1 よりも実験 2 の結果を予測するのが簡単です。したがって、結果から判断すると、実験 1 は実験 2 よりも不確実性が高く、この不確実性を測定するために特にエントロピーが使用されます。

実験結果の不確実性が大きければ、そのエントロピーは大きくなり、その逆も同様です。

完全に一定の結果が得られる決定論的な実験では、エントロピーはゼロです。公正なサイコロのような完全にランダムな実験では、それぞれの結果に大きな不確実性があり、エントロピーは大きくなります。

エントロピーを決定するもう 1 つの方法は、ランダムな実験の結果を観察するときに得られる平均情報を、エントロピーを定義する関数として使用することです。結果が少ないほど、観察される情報が少なくなり、エントロピーが低くなります。

たとえば、決定論的な実験では常に結果がわかっているため、観察から新しい情報は得られず、エントロピーはゼロになります。

数式

離散確率変数の場合

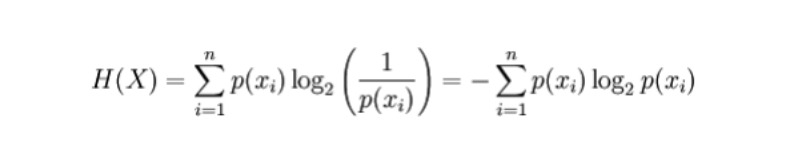
ここで、p(x_i) は変数 X によって生成される結果の確率です。

応用

• 自動決定ツリーを構築します。構築プロセス中に、エントロピーの基準を使用してすべての特徴を選択できます。

• エントロピーが大きいほど情報量が多くなり、予測値も大きくなります。これを使用して、2 つの競合するモデルから最も価値のあるモデル、つまりエントロピーが最も高いモデルを見つけることができます。

クロスエントロピー

意味：クロスエントロピーは主に 2 つの確率分布間の差異情報を測定するために使用され、2 つの確率がどの程度類似しているかを知ることができます。

数式

同じサンプルで定義された 2 つの確率 p と q のクロス エントロピーの計算式は次のとおりです (エントロピーは H、単位ビットで表されます)。

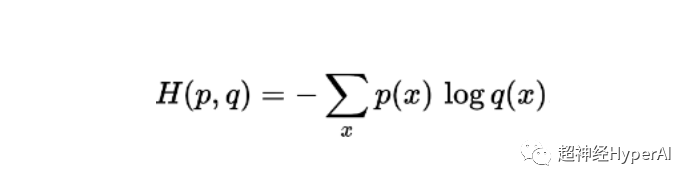
応用

• クロスエントロピー損失関数は、ロジスティック回帰などの分類モデルで広く使用されています。予測が真の出力から外れる場合、クロスエントロピー損失関数は増加します。

• CNN のような深層学習アーキテクチャでは、最終出力の「ソフトマックス」層でクロスエントロピー損失関数が使用されることがよくあります。

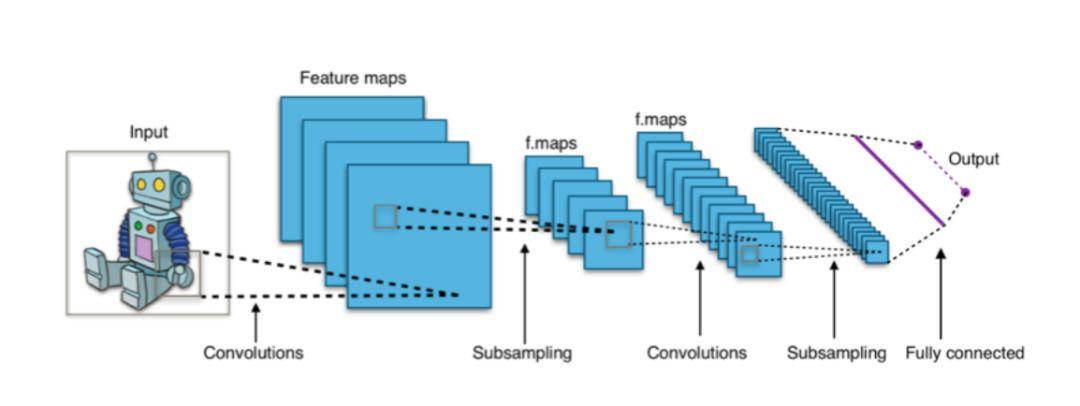
凡例: CNN ベースの分類器は通常、ソフトマックス層を最終層として使用し、トレーニングにクロスエントロピー損失関数を使用します。

相互情報

相互情報量は、2 つの確率分布または確率変数間の相互依存性の度合いを測定するために定義されます。簡単に言えば、ある変数の情報が別の変数にどの程度含まれているかを表します。

相互情報量によって捉えられる確率変数間の相関は、線形場に限定された一般的な相関とは異なり、一部の非線形相関情報も捉えることができ、その応用範囲はより広がります。

数式

2 つの離散確率変数 X と Y の相互情報量公式は次のとおりです。

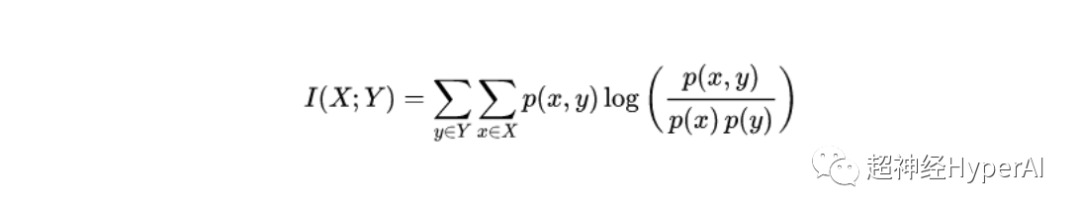
ここで、p(x,y) は x と y の同時確率分布であり、p(x) と p(y) はそれぞれ x と y の周辺確率分布です。

応用

• 特徴の選択: 相互情報は線形相関を捉えるだけでなく、非線形相関にも注意を払うことができるため、特徴の選択がより包括的かつ正確になります。
• ベイジアン ネットワークでは、相互情報量を使用して確率変数間の関係構造を学習し、これらの関係の強さを定義します。。

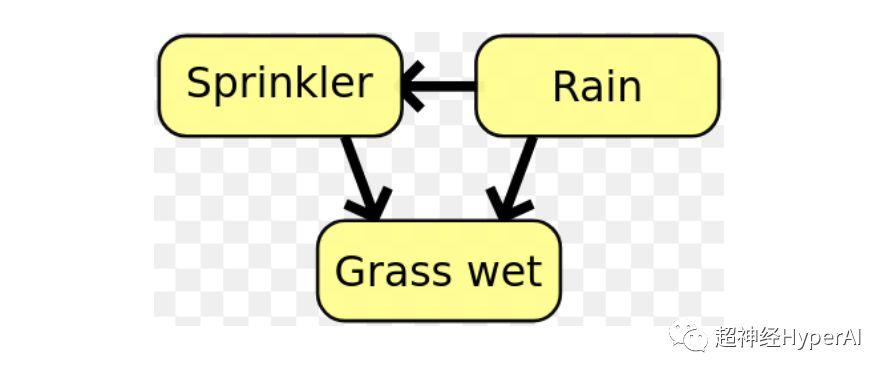
凡例: ベイジアン ネットワークでは、相互情報量を使用して変数間の関係構造を決定できます。

KL ダイバージェンス (カルバック-ライブラーダイバージェンス)

KL ダイバージェンスは相対エントロピーとも呼ばれ、2 つの確率分布の偏差を測定するために使用されます。

必要なデータは実分布 P にあると仮定しますが、この P はわかりません。この時点で、実分布 P に適合する新しい確率分布 Q を作成できます。

Q のデータは P に近似しているだけであるため、Q は P ほど正確ではありません。したがって、P と比較して、Q は部分的な情報損失を被ることになり、この損失した情報の量は KL 発散によって測定されます。

KL 発散は、Q (P の近似値) を使用することを決定したときにどれだけの情報が失われるかを示します。 KL 発散がゼロに近づくほど、Q のデータは P に近づきます。

数式

確率分布 Q と別の確率分布 P の間の KL 発散の数式は次のとおりです。

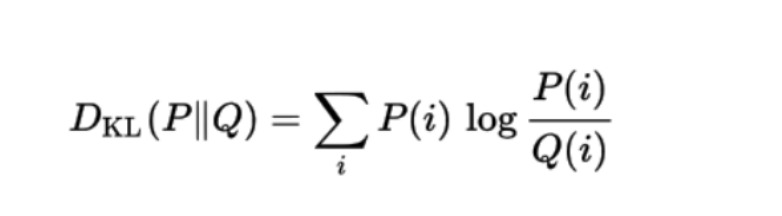
応用

KL ダイバージェンスは現在、教師なし機械学習システムの VAE (変分オートエンコーダー) で使用されています。

1948 年、クロード シャノンは画期的な論文「コミュニケーションの数学理論」で「情報理論」を正式に提案し、新しい時代の到来を告げました。今日、情報理論は機械学習、ディープラーニング、データサイエンスなどの多くの分野で広く使用されています。

周知のとおり、コンピュータ業界の最高栄誉賞はチューリング賞です。チューリング賞は、チューリングの傑出した貢献を記念して、アメリカ コンピュータ協会によって 1966 年に設立されました。同様に、シャノン賞も情報分野で同様に重要な役割を果たしています。

違いは、チューリングが 1954 年という早い時期に亡くなり、世界が彼のためにこの賞を設けたことを知る機会がなかったことです。

シャノン賞はより幸運です。 IEEE 協会は、情報理論の分野で優れた貢献をした科学者や技術者を表彰するために 1972 年に設立され、第 1 回セッションではシャノン自身がシャノン賞を受賞しました。

「シャノンは歴史上シャノンのルーティンとして知られるシャノン賞を受賞した」