Command Palette
Search for a command to run...
Paradigme d'entraînement par alignement de sous-espaces piloté par l'écart de modalité pour les modèles linguistiques à grande échelle multimodaux
Paradigme d'entraînement par alignement de sous-espaces piloté par l'écart de modalité pour les modèles linguistiques à grande échelle multimodaux
Résumé
Malgré les succès du apprentissage contrastif multimodal dans l’alignement des représentations visuelles et linguistiques, un anormalie géométrique persistante, appelée « Modality Gap » (écart modal), subsiste : les embeddings de modalités distinctes exprimant une sémantique identique occupent systématiquement des régions décalées. Les approches antérieures visant à combler cet écart sont largement limitées par des hypothèses isotropes trop simplifiées, ce qui entrave leur application dans des scénarios à grande échelle. Dans cet article, nous surmontons ces limitations en caractérisant précisément la forme géométrique de l’écart modal et en exploitant cette caractérisation pour permettre une mise à l’échelle efficace des modèles. Premièrement, nous proposons la Théorie de l’Écart Modal dans un Cadre Fixe, qui décompose l’écart modal dans un cadre de référence gelé en biais stables et en résidus anisotropes. Guidés par cette modélisation précise, nous introduisons ReAlign, une stratégie d’alignement modal sans entraînement. En exploitant des statistiques issues de données non appariées massives, ReAlign aligne la représentation textuelle sur la distribution des représentations visuelles via un processus en trois étapes : Alignement d’Ancre, Suivi (Trace) et Alignement du Centroid, corrigeant ainsi explicitement l’alignement géométrique. Sur la base de ReAlign, nous proposons ReVision, un paradigme évolutif pour les Modèles Linguistiques Multimodaux à Grande Échelle (MLLM). ReVision intègre ReAlign dans la phase de pré-entraînement, permettant au modèle d’apprendre la distribution des représentations visuelles à partir de textes non appariés avant l’ajustement par instruction visuelle, sans nécessiter de paires image-texte à grande échelle et de haute qualité. Notre cadre démontre qu’un alignement statistique des données non appariées peut efficacement remplacer les paires image-texte coûteuses, offrant ainsi une voie robuste pour la mise à l’échelle efficace des MLLM.
One-sentence Summary
Researchers from HKUST(GZ), NUS, and collaborators propose ReAlign and ReVision to resolve the modality gap in multimodal learning by modeling its geometric structure—stable bias and anisotropic residuals—enabling efficient, training-free alignment and scalable MLLM pretraining using unpaired data instead of costly image-text pairs.
Key Contributions
- We introduce the Fixed-frame Modality Gap Theory, which decomposes the geometric misalignment between visual and text embeddings into stable biases and anisotropic residuals within a frozen reference frame, correcting prior oversimplified isotropic assumptions.
- We propose ReAlign, a training-free alignment method that uses statistics from unpaired data to map text representations into the image embedding space via Anchor, Trace, and Centroid Alignment, enabling precise geometric correction without additional training.
- We present ReVision, a scalable MLLM pretraining paradigm that leverages ReAlign to substitute expensive image-text pairs with unpaired text data, allowing models to learn visual distributions before instruction tuning while maintaining performance.
Introduction
The authors leverage multimodal contrastive learning’s known geometric flaw—the Modality Gap—to rethink how Multimodal Large Language Models (MLLMs) are trained. Prior methods assume this gap is isotropic noise and correct only the mean shift, which fails to capture the true anisotropic structure of representation misalignment and limits scalability. The authors’ key contribution is a precise geometric decomposition of the gap into stable biases and anisotropic residuals, enabling ReAlign: a training-free, three-step statistical alignment that maps text embeddings into the visual distribution using only unpaired data. Building on this, they introduce ReVision, a scalable two-stage training paradigm that substitutes expensive image-text pairs with massive text during pretraining, then refines with real images—proving text alone can encode rich visual semantics when aligned correctly.
Method
The authors leverage a fixed-reference framework to decompose the modality gap into interpretable geometric components, enabling precise characterization of persistent misalignments in dual-encoder contrastive models. This decomposition is grounded in a data-driven subspace construction that separates bias and residual terms, allowing independent estimation and reducing theoretical claims to second-moment conditions estimable from finite samples.
The framework begins by training a dual-encoder model using the InfoNCE loss on a large-scale image-text dataset. At a fixed reference time t0, a task-relevant subspace U is constructed from a held-out probe set by computing the empirical covariance of unit-normalized embeddings for both modalities:
Σ^(t0):=Covp(ex(t0))+Covp(ey(t0)),where U:=span{q1,…,qr} is derived from the top r eigenvectors of Σ^(t0), determined by an energy threshold. The orthogonal complement V:=U⊥ is then defined, and fixed orthogonal projectors PU and PV are maintained for all subsequent analysis. This fixed frame enables consistent decomposition of the modality gap Δ(t):=ex(t)−ey(t) into bias and residual components.
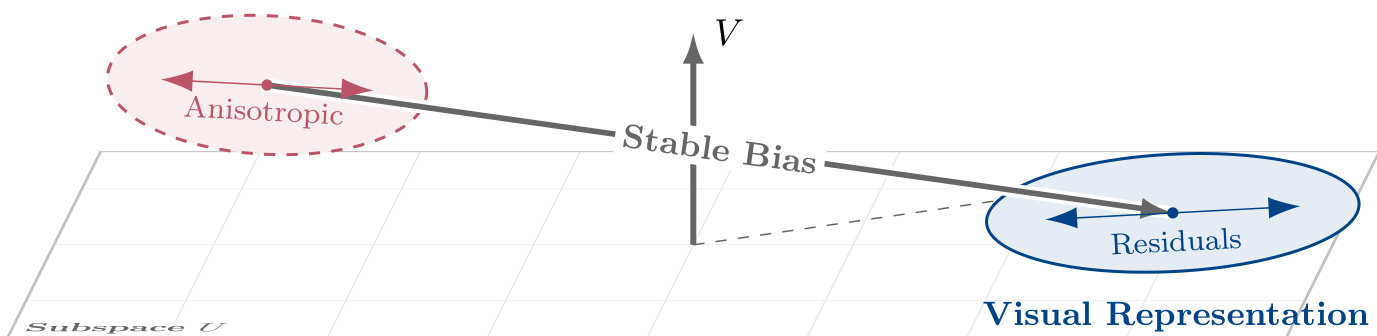
The bias terms are defined as projected mean components: β(t):=PUE[Δ(t)]∈U (Principal Modality Bias, PMB) and γ(t):=PVE[Δ(t)]∈V (Constant Orthogonal Bias, COB). The zero-mean residuals are δ(t):=PU(Δ(t)−E[Δ(t)])∈U and ζ(t):=PV(Δ(t)−E[Δ(t)])∈V. This yields the exact orthogonal decomposition:
Δ(t)=β(t)+δ(t)+γ(t)+ζ(t).As shown in the figure below, the residual structure exhibits extreme anisotropy in both subspaces, with the orthogonal component V hosting a stable bias vector that remains geometrically decoupled from the highly stretched noise structure of ζ(t).
The authors further analyze the evolution of these components. Gradients are empirically observed to concentrate within the instantaneous task subspace Ut, with the reference leakage ratio ∥PVgt∥/∥gt∥ tightly tracking the geometric baseline sinθ(Ut,U). This concentration implies that direct optimization in V is negligible, leading to passive drift of γ(t) — a slow, cumulative evolution driven by subspace rotation rather than active gradient correction. In contrast, within U, the residual δ(t) exhibits extreme anisotropy (κ(ΣU)>103) and rapidly aligns with the gradient covariance structure, indicating that fluctuations are semantically coupled to the task.
To address these geometric misalignments without retraining, the authors propose ReAlign, a three-stage, training-free alignment strategy. The method operates in Euclidean space before spherical projection and consists of:
- Anchor Alignment: Centering the source modality and shifting its mean to match the target’s centroid: e˙y=(ey−μy)+μx.
- Trace Alignment: Scaling the residuals to match the target’s global energy via s=Tx/Ty, yielding e~y=μx+s(ey−μy), preserving the source’s anisotropic structure.
- Centroid Alignment: Correcting the non-linear drift induced by spherical projection by explicitly re-centering the distribution: ey′′=ey′−μ′+μx, followed by re-normalization.
As illustrated in the ReAlign pipeline, this sequence ensures that the final aligned representation matches both the first- and second-order statistics of the target modality on the unit hypersphere, while preserving semantic hierarchy and mitigating phantom drift.

This geometrically grounded approach forms the foundation for ReVision, a scalable two-stage training paradigm for multimodal LLMs. In Stage 1, ReAlign is used to synthesize pseudo-visual embeddings from unpaired text, enabling pretraining on vast textual corpora. In Stage 2, the model is fine-tuned on real image-instruction pairs to refine fine-grained visual reasoning. During inference, the model directly consumes real images, benefiting from the asymmetric alignment established during pretraining.
Experiment
- ReAlign effectively reduces modality gap by modeling anisotropic covariance, outperforming isotropic methods like C³ that hit geometric bottlenecks.
- ReVision achieves superior performance in multimodal LLM training by preserving semantic hierarchy and angular topology, leading to better reasoning and reduced hallucinations.
- Scaling unpaired text data (2M samples) with ReAlign surpasses performance of 1M real image-text pairs at 26% lower cost, proving cost-efficient scaling is viable.
- ReAlign demonstrates rapid convergence with ~10K samples, stable numerical precision in Float64, linear time complexity, and constant memory usage, enabling scalable deployment.
- Domain-specific statistics are essential; cross-domain alignment degrades performance, highlighting the need for tailored calibration.
- Blockwise covariance alignment fails due to numerical instability and semantic distortion, while ReAlign’s isotropic scaling preserves local structure and ensures robustness.
- Short captions outperform long ones due to compact, low-rank covariance and higher signal-to-noise ratio, revealing that linguistic density can harm geometric alignment.
- Qualitative analysis confirms ReVision excels in abstract reasoning, spatial understanding, fine-grained perception, and knowledge integration across diverse cognitive tasks.
ReVision outperforms BC Align across all evaluated categories, including general perception, complex reasoning, and hallucination resistance, achieving a higher average score. The results confirm that ReVision’s geometric alignment strategy preserves semantic structure better than blockwise covariance methods, which suffer from numerical instability and semantic distortion. This leads to more robust and accurate multimodal understanding without requiring paired image-text data.

Results show that ReVision, which uses anisotropic geometric alignment, consistently outperforms its long-caption variant across general perception, reasoning, and hallucination benchmarks. The performance gap highlights that concise, geometrically compact captions enable more stable modality alignment than linguistically rich but noisy long captions. This suggests that signal-to-noise ratio and manifold structure matter more than raw textual length for effective cross-modal training.

The authors use ReVision to align text and image modalities by modeling anisotropic covariance, which significantly reduces the geometric gap compared to isotropic methods like C³. Results show that ReVision outperforms baselines across general perception, reasoning, and hallucination benchmarks, demonstrating that precise geometric alignment preserves semantic structure and improves downstream task performance. Scaling up text-only pretraining with ReVision also surpasses paired image-text training in performance while reducing data acquisition costs.

ReVision-2M achieves the highest average score across general, reasoning, and hallucination benchmarks, outperforming both text-only and paired image-text baselines while reducing data acquisition cost by 26%. The method’s geometric alignment strategy preserves semantic structure better than isotropic noise-based approaches, enabling superior performance even without real image inputs. Scaling up unpaired text data with precise alignment proves more cost-effective and competitive than relying on expensive paired datasets.
