One-sentence Summary

Researchers from Peking University and Tencent Hunyuan propose iFSQ, a refined scalar quantization that fixes activation collapse via distribution-matching, enabling fair AR-diffusion benchmarking; they reveal 4 bits/dim as optimal and show diffusion models surpass AR in ceiling performance, extending insights to LlamaGen-REPA.

Key Contributions

• We introduce iFSQ, a one-line-code enhancement to Finite Scalar Quantization that replaces the tanh activation with a distribution-matching function, ensuring uniform bin utilization and optimal reconstruction fidelity by mapping Gaussian latents to a uniform prior.
• Using iFSQ as a unified tokenizer, we establish a controlled benchmark revealing that 4 bits per dimension strikes the optimal balance between discrete and continuous representations, and that diffusion models outperform autoregressive models in final quality despite slower convergence.
• We adapt Representation Alignment (REPA) to autoregressive image generation, creating LlamaGen-REPA with stronger regularization (λ=2.0), demonstrating improved performance while confirming the benefit of feature alignment across generative paradigms.

Introduction

The authors leverage Finite Scalar Quantization (FSQ) to unify autoregressive and diffusion image generation under a single tokenizer, addressing the long-standing fragmentation caused by VQ-VAEs and VAEs. Vanilla FSQ suffers from activation collapse due to equal-interval quantization mismatching the Gaussian-like distribution of neural activations, forcing a trade-off between reconstruction fidelity and bin utilization. Their main contribution is iFSQ — a one-line code modification replacing tanh with a distribution-matching activation — which enforces uniform prior while preserving equal intervals, achieving optimal fidelity and efficiency simultaneously. This enables fair benchmarking, revealing that 4 bits per dimension is the sweet spot and that diffusion models outperform AR models in peak quality despite slower convergence. They further extend this by adapting Representation Alignment to AR models, creating LlamaGen-REPA.

Method

The authors leverage a quantization-based framework for visual tokenization that bridges the gap between continuous and discrete representation paradigms in generative models. The core of this approach is built upon Finite Scalar Quantization (FSQ), which enables a discrete tokenization process without the need for an explicit, learnable codebook. This design allows for efficient and stable tokenization suitable for both autoregressive and diffusion-based generation tasks. The tokenizer architecture consists of an encoder that compresses input images $x \in \mathbb{R}^{H \times W \times 3}$x∈RH×W×3 into a lower-resolution latent representation $z \in \mathbb{R}^{h \times w \times d}$z∈Rh×w×d, typically through an $8\times$8× or $16\times$16× downsampling process. The decoder then reconstructs the image from the latent space, forming a complete compression-decompression pipeline.

For diffusion models, the quantized latent $z_{\text{quant}}$zquant​ is used directly as input to the diffusion process. The quantization is performed by first applying a bounding function $f: \mathbb{R} \to [-1, 1]$f:R→[−1,1], commonly the hyperbolic tangent function, to constrain the latent values. The quantization resolution is defined by $L = 2^K + 1$L=2K+1 levels per channel, where $K$K determines the number of quantization levels. The continuous latent $z$z is mapped to discrete integer indices $q \in \{0, \ldots, L-1\}^d$q∈{0,…,L−1}d via element-wise rounding, as defined by the equation:

This operation maps the range $[-1, 1]$[−1,1] to the integer set $\{0, \ldots, L-1\}${0,…,L−1}. The quantized indices are then mapped back to the continuous space for diffusion models using:

This step introduces a lossy compression, where $z_{\mathrm{quant}} \approx z$zquant​≈z, preserving the structural properties of the continuous latent space while enabling discrete tokenization.

For autoregressive models, the quantized indices $q$q are converted into a single scalar token index $I$I through a bijective base-$L$L expansion:

This transformation ensures a unique mapping from the $d$d-dimensional quantized vector to a scalar index, enabling the use of autoregressive models that predict tokens sequentially. The implicit codebook size is $|\mathcal{C}| = L^d$∣C∣=Ld, which grows exponentially with the dimensionality $d$d, but avoids the memory and stability issues associated with learnable codebooks in VQ-VAE.

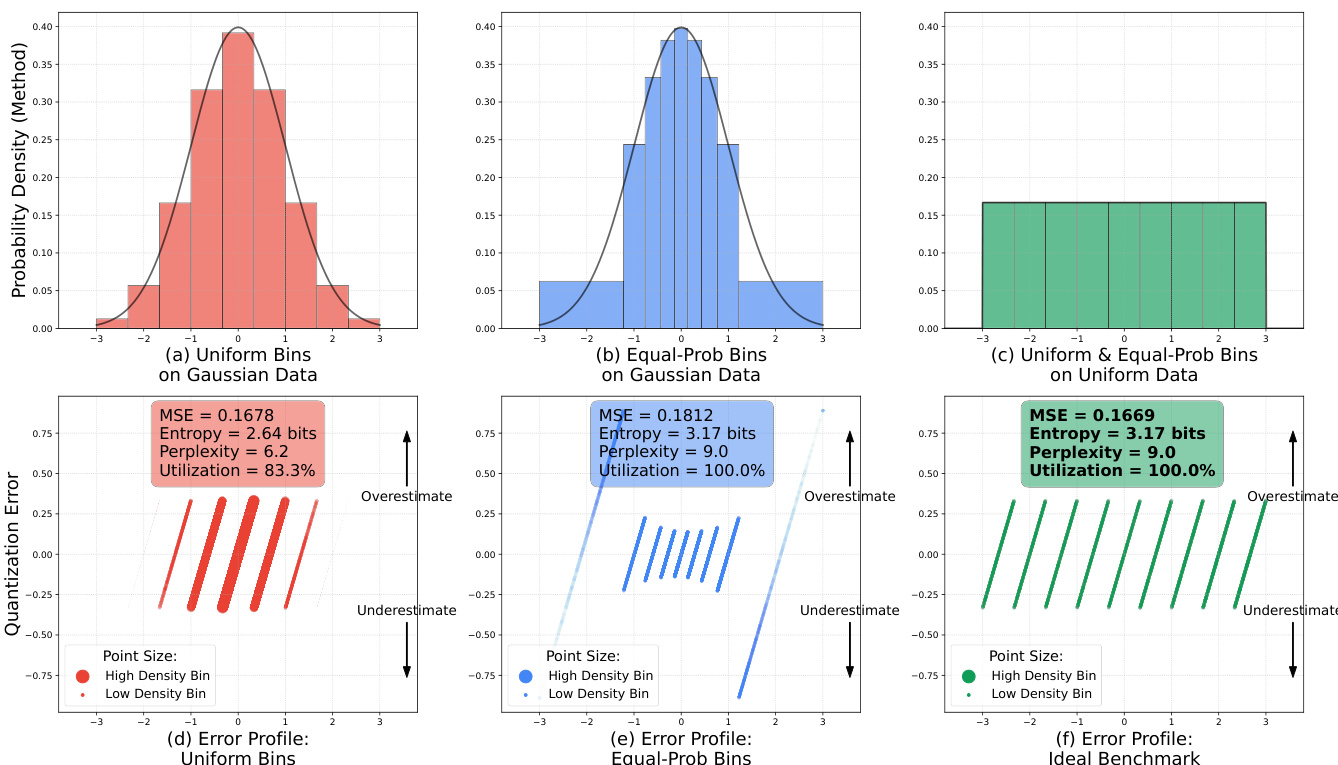
The authors introduce a modification to the standard FSQ pipeline by replacing the tanh activation with a scaled sigmoid function to achieve a more uniform distribution of quantized values. Specifically, the bounding function is replaced as follows:

This change improves the uniformity of the transformed distribution, which is critical for maintaining the quality of the quantized representation. The quantization process is further refined using a straight-through estimator to handle gradient flow during training. The rounded latent $z_{\text{rounded}}$zrounded​ is computed as:

where $z_{\text{scaled}} = z \cdot \text{halfWidth}$zscaled​=z⋅halfWidth, and $\text{halfWidth} = (L - 1)/2$halfWidth=(L−1)/2. The estimator is then applied as:

This allows gradients to pass through the rounding operation during backpropagation. Finally, for diffusion models, the quantized latent is normalized by dividing by the half-width:

This normalization ensures that the quantized latent remains within the $[-1, 1]$[−1,1] range, consistent with the input distribution.

Experiment

• Optimized iFSQ via α=1.6 in sigmoid-based activation achieves near-uniform output distribution, minimizing RMSE and KS metrics vs. tanh (α=2.0), improving reconstruction fidelity and entropy utilization.
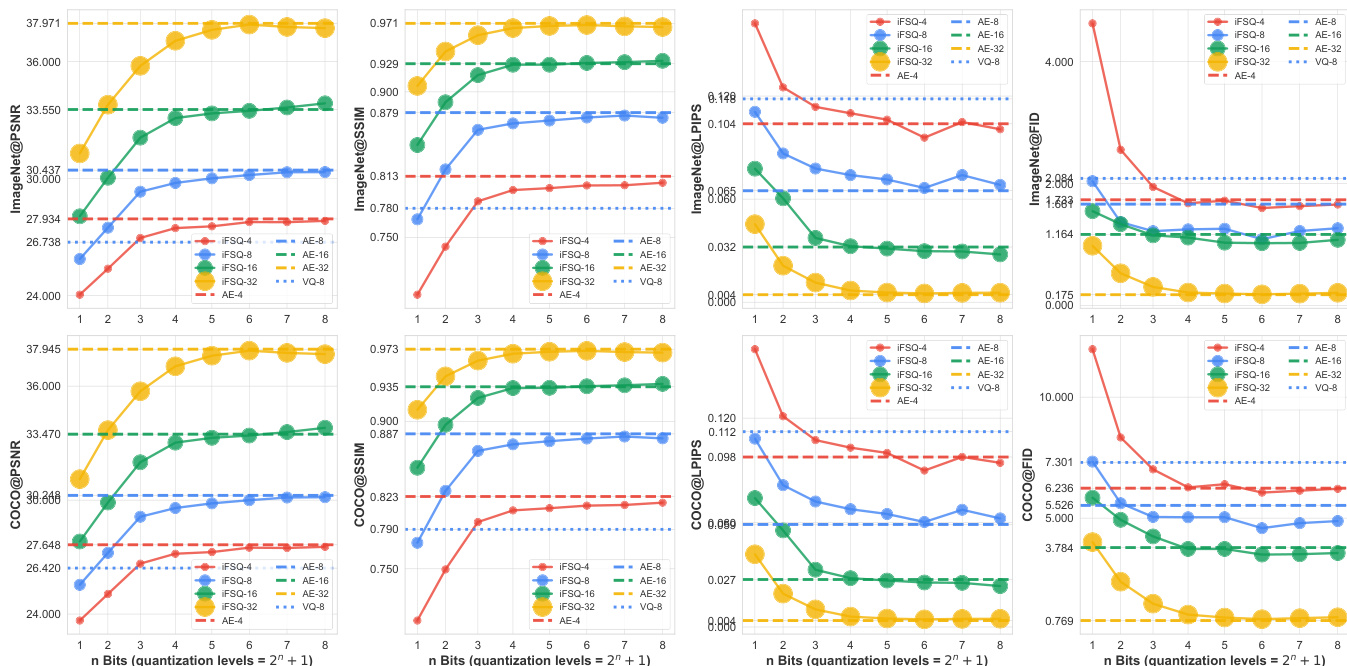
• On ImageNet, iFSQ (α=1.6) outperforms FSQ in PSNR, SSIM, and LPIPS; trends replicate on COCO, confirming scalability.
• For diffusion generation (DiT), iFSQ at 4 bits achieves gFID 12.76 (vs. AE’s 13.78) with 3× higher compression (96 vs. 24); performance plateaus beyond 4 bits.
• For autoregressive generation (LlamaGen), iFSQ outperforms VQ at same latent dimension and lower bit rate; 4-bit iFSQ matches AE, with performance peaking at 4 bits.
• iFSQ enables fair comparison of diffusion vs. AR models: diffusion converges slower but surpasses AR in FID at higher compute; AR models exhibit strong sequential constraint limitations.
• iFSQ scales favorably: at 2 bits, double latent dim surpasses AE; at 7–8 bits, matches or exceeds AE; outperforms VQ across quantization levels and dimensions.
• REPA alignment at 1/3 network depth (e.g., layer 8/24) optimizes semantic acquisition in LlamaGen; λ=2.0 yields best FID, differing from DiT’s optimal λ.
• Compression ratio scaling (fig. 10) shows linear performance trend with optimal knee at ~48× compression (4 bits); VQ aligns closely with iFSQ trend, validating its hybrid discrete-continuous nature.

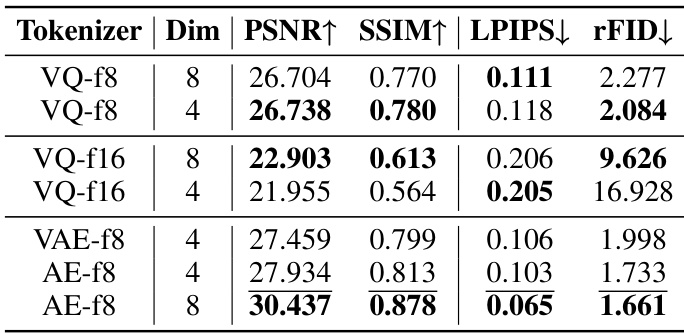
The authors compare various tokenizers, including VQ and AE variants, and find that AE-f8 achieves the highest PSNR and SSIM while also yielding the lowest LPIPS and rFID scores, indicating superior reconstruction quality. Among the VQ-based tokenizers, VQ-f8 outperforms VQ-f16 in all metrics, suggesting that higher quantization levels improve reconstruction performance.

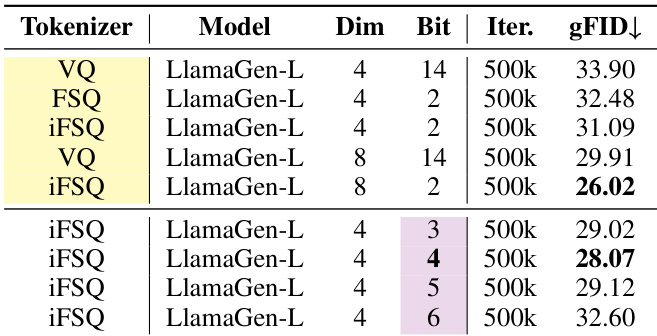
Results show that iFSQ at 2 bits achieves the lowest gFID of 26.02, outperforming VQ-VAE and FSQ under the same settings. The performance degrades as the bit rate increases beyond 2 bits, with iFSQ at 4 bits achieving a gFID of 28.07, indicating that lower quantization levels are optimal for this configuration.

Results show that iFSQ with α = 1.6 achieves the best performance across PSNR, SSIM, and LPIPS, outperforming the original FSQ (α = 2.0), while also minimizing RMSE and KS statistics, indicating a near-uniform distribution. The optimal setting at α = 1.6 balances fidelity and distributional alignment, leading to superior image reconstruction quality compared to both continuous and discrete baselines.

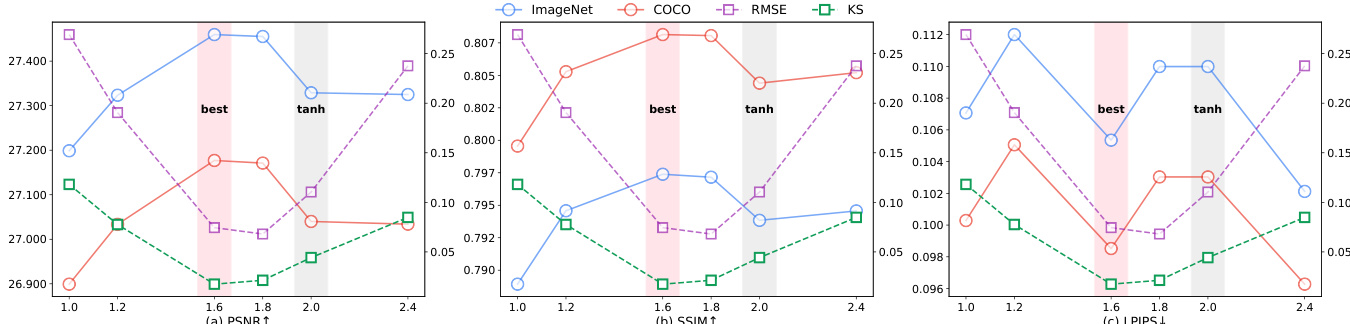
The authors use iFSQ to optimize the distribution of latent features in image generation models, showing that setting the activation parameter α to 1.6 achieves a near-uniform distribution, which improves reconstruction quality and generation performance. Results show that iFSQ at 4 bits matches or exceeds the performance of continuous AE and VQ-VAE across metrics like PSNR, SSIM, and FID, while maintaining a higher compression ratio and better training efficiency.

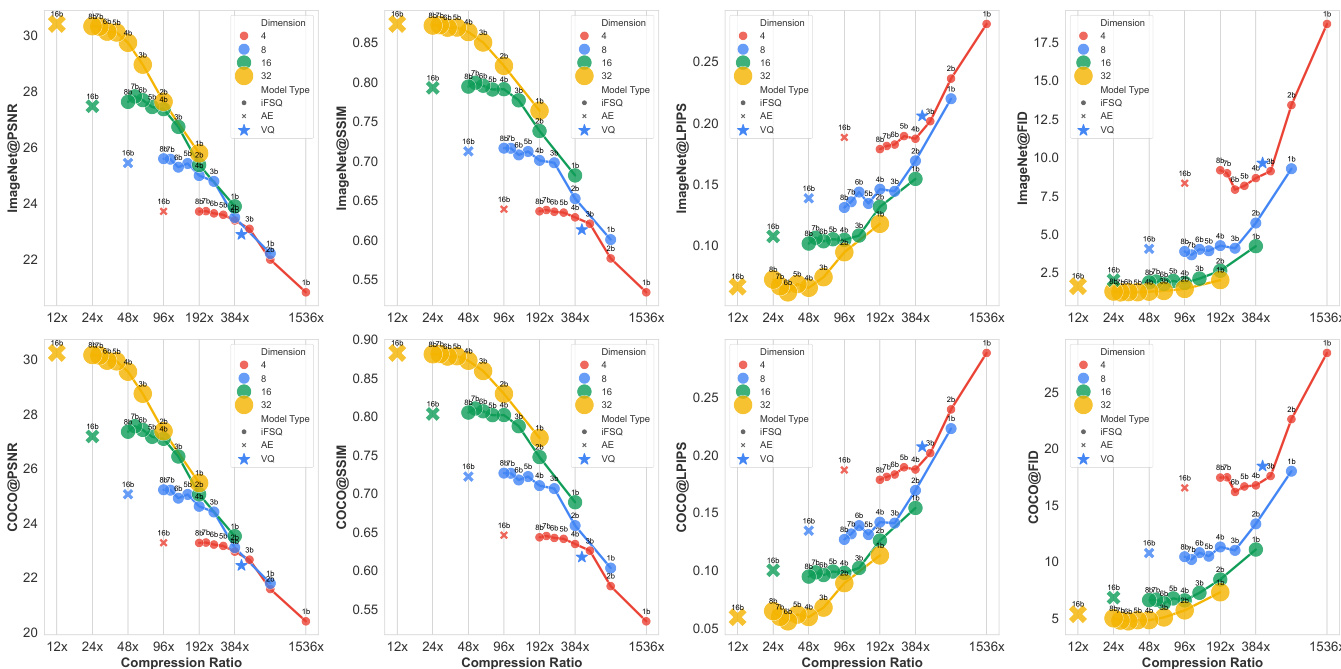
Results show that iFSQ with 4 bits achieves the best balance between reconstruction and generation performance, outperforming both AE and VQ-VAE across PSNR, SSIM, and LPIPS metrics while maintaining a significantly higher compression rate. The optimal performance at 4 bits aligns with the theoretical analysis, where the distribution of iFSQ's activations most closely approximates a uniform distribution, maximizing information entropy and minimizing activation collapse.