Command Palette
Search for a command to run...
AdaGaR : Représentation de Gabor adaptative pour la reconstruction de scènes dynamiques
AdaGaR : Représentation de Gabor adaptative pour la reconstruction de scènes dynamiques
Jiewen Chan Zhenjun Zhao Yu-Lun Liu
Résumé
La reconstruction de scènes 3D dynamiques à partir de vidéos monoculaires nécessite la capture simultanée de détails d’apparence à haute fréquence et d’un mouvement temporelment continu. Les méthodes existantes basées sur des primitives gaussiennes simples sont limitées par leur nature passe-bas, tandis que les fonctions standard de Gabor introduisent une instabilité énergétique. En outre, le manque de contraintes de continuité temporelle entraîne fréquemment des artefacts de mouvement lors des interpolations. Nous proposons AdaGaR, un cadre unifié qui traite à la fois l’adaptabilité fréquentielle et la continuité temporelle dans la modélisation explicite des scènes dynamiques. Nous introduisons une représentation adaptative de Gabor, étendant les gaussiennes grâce à des poids de fréquence apprenables et une compensation énergétique adaptative, afin d’équilibrer la capture de détails et la stabilité. Pour assurer la continuité temporelle, nous utilisons des splines de Hermite cubiques avec une régularisation de courbure temporelle, garantissant une évolution fluide du mouvement. Un mécanisme d’initialisation adaptative combinant l’estimation de profondeur, le suivi de points et des masques d’objet frontal permet d’établir des distributions de nuages de points stables dès les premières étapes d’entraînement. Des expériences sur le jeu de données Tap-Vid DAVIS montrent des performances de pointe (PSNR : 35,49, SSIM : 0,9433, LPIPS : 0,0723) et une forte généralisation pour l’interpolation d’images, la cohérence de profondeur, le traitement vidéo et la synthèse de vues stéréo. Page du projet : https://jiewenchan.github.io/AdaGaR/
One-sentence Summary
The authors from National Yang Ming Chiao Tung University and University of Zaragoza propose AdaGaR, a unified framework for dynamic 3D scene reconstruction that introduces an Adaptive Gabor Representation with learnable frequency weights and energy compensation to achieve high-frequency detail preservation and stability, while employing Cubic Hermite Splines with temporal curvature regularization to ensure smooth motion, outperforming prior methods in video reconstruction, frame interpolation, and view synthesis.
Key Contributions
-
We introduce Adaptive Gabor Representation, a frequency-adaptive extension of 3D Gaussians that learns dynamic frequency weights and applies adaptive energy compensation to simultaneously preserve high-frequency textures and maintain rendering stability, overcoming the low-pass filtering limitation of standard Gaussians and the energy instability of fixed Gabor functions.
-
We propose Temporal Curvature Regularization with Cubic Hermite Splines to enforce smooth motion trajectories over time, ensuring geometric and temporal continuity in dynamic scene reconstruction and effectively eliminating interpolation artifacts, especially under rapid motion or occlusions.
-
We design an Adaptive Initialization mechanism that integrates monocular depth estimation, point tracking, and foreground masks to establish temporally coherent and stable point cloud distributions early in training, significantly improving convergence and final reconstruction quality on the Tap-Vid DAVIS dataset.
Introduction
Reconstructing dynamic 3D scenes from monocular videos is critical for applications in VR, AR, and film production, where both smooth temporal motion and high-fidelity texture representation are essential. Prior methods using Gaussian-based primitives struggle with high-frequency detail due to inherent low-pass filtering, while frequency-enhancing approaches like Gabor representations often compromise energy stability and rendering quality. Many also lack explicit temporal constraints, leading to motion artifacts under rapid motion or occlusions. The authors introduce AdaGaR, a unified framework that jointly optimizes time and frequency in explicit dynamic representations. It features an Adaptive Gabor Representation that learns frequency response for balanced high- and low-frequency modeling with energy stability, and Temporal Curvature Regularization via Cubic Hermite Splines to enforce smooth motion trajectories. An Adaptive Initialization mechanism leverages depth, motion, and segmentation priors to bootstrap stable, temporally coherent geometry. The approach achieves state-of-the-art results on Tap-Vid, demonstrating strong generalization across video reconstruction, interpolation, depth consistency, editing, and stereo synthesis.
Method
The authors leverage a unified framework, AdaGaR, to address the dual challenges of frequency adaptivity and temporal continuity in explicit dynamic scene modeling from monocular videos. The overall architecture, as illustrated in the framework diagram, operates within an orthographic camera coordinate system, which simplifies the representation by treating camera and object motion as a single dynamic variation, avoiding the need for explicit camera pose estimation. The core of the method consists of two primary components: Adaptive Gabor Representation and Adaptive Motion, which are optimized jointly with a multi-supervision loss function.
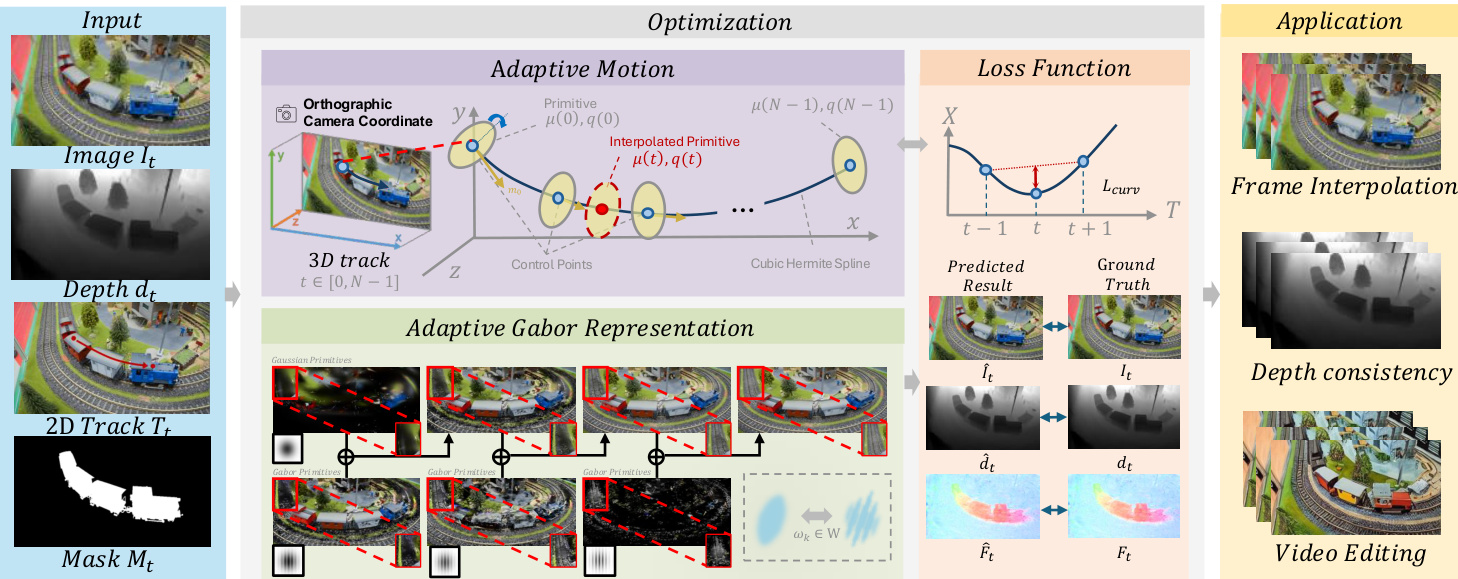
The Adaptive Gabor Representation extends the standard 3D Gaussian Splatting primitive to capture high-frequency appearance details. It achieves this by modulating the traditional Gaussian density function with a learnable, periodic sinusoidal component. The Gabor function, defined as GGabor(x)=exp(−21∣∣x−μ∣∣Σ−12)cos(f⊤x+ϕ), introduces a sinusoidal modulation within the Gaussian envelope, enabling the representation of local directional textures. To model richer frequency components, multiple Gabor waves are combined into a weighted superposition, S(x)=∑i=1Nωicos(fi⟨di,x⟩+ϕi), where the amplitude weights ωi are learnable parameters. To ensure energy stability and prevent intensity attenuation, a compensation term b is introduced, resulting in the final adaptive modulation function Sadap(x)=b+N1∑i=1Nωicos(fi⟨di,x⟩). This formulation allows the representation to adaptively span from a low-frequency Gaussian to a high-frequency Gabor kernel, with the compensation term ensuring a smooth degradation to a standard Gaussian when frequency weights vanish.

The Adaptive Motion component ensures temporally smooth and consistent motion evolution. It models the trajectory of each dynamic primitive using Cubic Hermite Splines, which interpolate the positions and velocities at a set of temporal keyframes. The spline interpolation is defined by the Hermite basis functions, which use control points yk and slopes mk to generate a smooth curve. To prevent reverse oscillations and ensure visually stable interpolation, an auto-slope mechanism with a monotone gate is employed, which sets the slope to zero if the direction of motion changes between adjacent keyframes. For rotation, the same principle is applied by interpolating in the so(3) Lie algebra space and converting to unit quaternions. To enforce smoothness and prevent motion artifacts, a temporal curvature regularization term is introduced, which penalizes the second-order derivative of the trajectory at each keyframe, thereby constraining the motion to be geometrically and temporally consistent.
The optimization process is driven by a multi-objective loss function that combines several supervisory signals. Rendering reconstruction loss, a combination of L1 and SSIM, ensures appearance fidelity. Optical flow consistency loss, derived from Co-Tracker, aligns the projected positions of the primitives with ground-truth 2D trajectories. Depth loss, using monocular depth estimates from DPT, provides geometric priors. Finally, the curvature regularization loss Lcurv enforces smooth temporal evolution. The total loss is a weighted sum of these components, enabling the model to achieve both high-fidelity rendering and robust temporal consistency. An adaptive initialization mechanism, which fuses multi-modal cues from depth, tracking, and masks, is used to generate a dense and temporally coherent initial point cloud, reducing early-stage flickering and improving convergence.
Experiment
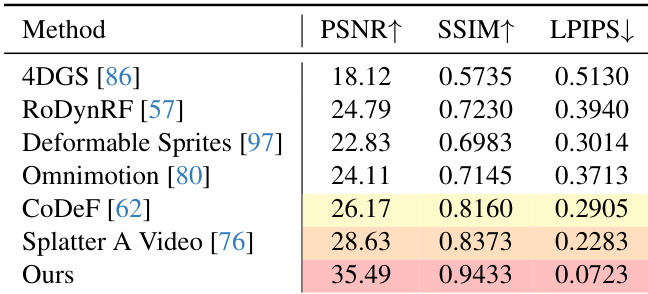
- AdaGaR achieves state-of-the-art video reconstruction on Tap-Vid DAVIS, attaining 35.49 dB PSNR and 0.9433 SSIM, with 6.86 dB PSNR improvement over the second-best method, while preserving fine details and temporal consistency.
- Ablation studies validate the effectiveness of Adaptive Gabor Representation, Cubic Hermite Spline with curvature regularization, and adaptive initialization, showing superior performance in high-frequency detail preservation, motion smoothness, and depth consistency.
- The method enables robust downstream applications: frame interpolation produces smooth, artifact-free intermediate frames with preserved texture details; video editing maintains temporal coherence through shared canonical primitives; stereo view synthesis achieves plausible geometry from monocular input.
- On Tap-Vid DAVIS, the approach outperforms baselines across PSNR, SSIM, and LPIPS, with training completed in 90 minutes per sequence on an NVIDIA RTX 4090.
Results show that the proposed method achieves state-of-the-art performance on the Tap-Vid DAVIS dataset, outperforming all baselines across PSNR, SSIM, and LPIPS metrics. It achieves a PSNR of 35.49 dB, 6.86 dB higher than the second-best method, Splatter A Video, while also demonstrating superior texture detail and temporal consistency.
Results show that the proposed Cubic Hermite Spline achieves the highest PSNR and SSIM scores while minimizing LPIPS, outperforming both B-Spline and Cubic Spline across all metrics. The authors use this method to generate smooth intermediate frames, demonstrating superior temporal coherence and preservation of high-frequency details.

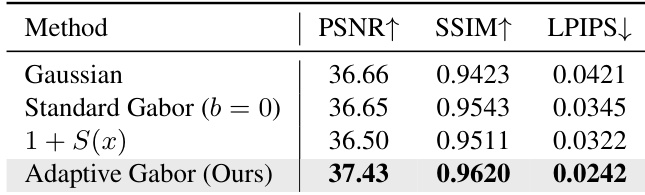
The authors use an ablation study to compare different Gabor representation variants, showing that the Adaptive Gabor method achieves the highest PSNR and SSIM while minimizing LPIPS, indicating superior reconstruction quality and perceptual fidelity. Results demonstrate that the adaptive formulation with the compensation term b outperforms standard Gaussian and naive Gabor configurations across all metrics.