One-sentence Summary

The authors from DeepSeek-AI propose $m$mHC, a manifold-constrained framework that restores identity mapping in Hyper-Connections by projecting residual matrices onto a geometric manifold, enabling stable, scalable training with reduced memory overhead while maintaining the flexibility and performance gains of prior hyper-connectivity designs.

Key Contributions

• The paper addresses the instability and scalability limitations of Hyper-Connections (HC), which expand residual stream width and connectivity patterns but disrupt the identity mapping property essential for stable training in deep networks.
• It introduces Manifold-Constrained Hyper-Connections ($m$mHC), a framework that projects residual connection matrices onto a doubly stochastic manifold using the Sinkhorn-Knopp algorithm, thereby restoring identity mapping and enabling stable, large-scale training.
• Empirical evaluations show $m$mHC achieves superior scalability and performance over HC, with negligible computational overhead due to infrastructure optimizations like kernel fusion, recomputing, and communication overlapping.

Introduction

The authors leverage recent advances in macro-architecture design—particularly Hyper-Connections (HC), which expand residual stream width and diversify inter-layer connectivity—to improve model expressiveness and performance in large language models. However, prior HC methods suffer from training instability and poor scalability due to the loss of the identity mapping property, which disrupts signal conservation across layers, and incur high memory access overhead from widened feature representations. To address these issues, the authors propose Manifold-Constrained Hyper-Connections (mHC), a framework that projects residual connection matrices onto a doubly stochastic manifold using the Sinkhorn-Knopp algorithm, thereby restoring identity mapping and stabilizing signal propagation. This geometric constraint ensures convex combination-based feature flow, enabling robust large-scale training. Complementing this, mHC integrates infrastructure optimizations—including kernel fusion, recomputation, and overlapping communication in DualPipe—to minimize computational overhead. The result is a scalable, stable, and efficient extension of HC that preserves performance gains while enabling deeper and wider model architectures.

Dataset

• The dataset comprises multiple text sources used to train the 3B, 9B, and 27B variants of the DeepSeek-V3 model, drawing from diverse public and curated corpora.
• The training data is split into distinct subsets, each with specific size, source, and filtering rules: high-quality web text, code repositories, academic papers, and multilingual content, all processed to remove low-quality or redundant samples.
• The authors use a mixture-of-experts (MoE) training strategy with dynamic routing, where the data is distributed across experts based on input content, and the model is trained using a weighted mixture of these subsets with carefully tuned ratios to balance coverage and quality.
• Data preprocessing includes tokenization with a 128K vocabulary, length filtering to cap sequences at 32K tokens, and a cropping strategy that samples fixed-length segments from longer documents to ensure consistent input size during training.
• Metadata such as source type, language, and content category are constructed during preprocessing to support dynamic sampling and curriculum learning during training.

Method

The authors leverage a novel framework, Manifold-Constrained Hyper-Connections (mHC), to address the stability and scalability limitations of the Hyper-Connections (HC) architecture in large-scale deep learning models. The core of mHC is a constrained residual connection mechanism that projects the residual mapping onto a specific manifold to preserve the identity mapping property, which is crucial for stable signal propagation across many layers. The overall framework extends the standard residual block by introducing a multi-stream residual design, where the input feature vector $\mathbf{x}_l$xl​ is expanded into an $n \times C$n×C matrix, forming $n$n parallel residual streams. This expansion allows for richer information exchange within the residual path. The propagation of a single layer in mHC is defined as $\mathbf{x}_{l+1} = \mathcal{H}_l^{\text{res}} \mathbf{x}_l + \mathcal{H}_l^{\text{post}^\top} \mathcal{F}(\mathcal{H}_l^{\text{pre}} \mathbf{x}_l, \mathcal{W}_l)$xl+1​=Hlres​xl​+Hlpost⊤​F(Hlpre​xl​,Wl​), where $\mathcal{F}$F is the base layer function (e.g., a feed-forward network), and $\mathcal{H}_l^{\text{pre}}$Hlpre​, $\mathcal{H}_l^{\text{post}}$Hlpost​, and $\mathcal{H}_l^{\text{res}}$Hlres​ are learnable linear mappings that manage the dimensional mismatch between the $nC$nC-dimensional residual stream and the $C$C-dimensional layer input/output. The key innovation lies in the constraint applied to the residual mapping $\mathcal{H}_l^{\text{res}}$Hlres​. Instead of being unconstrained, it is projected onto the manifold of doubly stochastic matrices, also known as the Birkhoff polytope. This projection ensures that the matrix has non-negative entries and that both its row and column sums equal one. This constraint is critical because it guarantees that the operation $\mathcal{H}_l^{\text{res}} \mathbf{x}_l$Hlres​xl​ acts as a convex combination of the input features, thereby conserving the global mean of the features and preventing unbounded signal amplification or attenuation during deep network propagation. The authors further impose non-negativity constraints on the input and output mappings $\mathcal{H}_l^{\text{pre}}$Hlpre​ and $\mathcal{H}_l^{\text{post}}$Hlpost​ to prevent signal cancellation.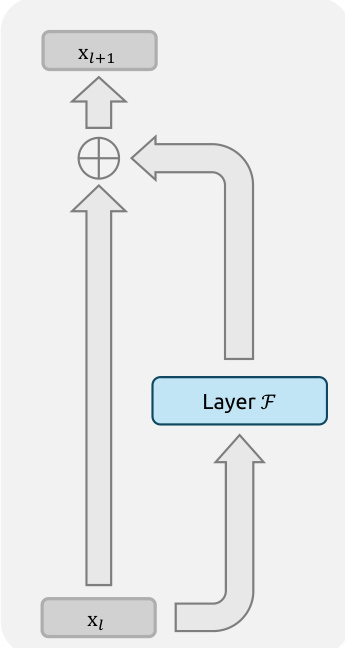

The parameterization of the mHC mappings is designed to be efficient and differentiable. The learnable parameters are derived from the input hidden matrix $\mathbf{x}_l$xl​ through a combination of dynamic and static mappings. The dynamic mappings are computed using linear projections parameterized by $\varphi_l$φl​, while the static mappings are represented by learnable biases $\mathbf{b}_l$bl​. The final constrained mappings are obtained by applying specific functions to the unprojected parameters. The input and output mappings $\mathcal{H}_l^{\text{pre}}$Hlpre​ and $\mathcal{H}_l^{\text{post}}$Hlpost​ are constrained to be non-negative using the Sigmoid function. The residual mapping $\mathcal{H}_l^{\text{res}}$Hlres​ is projected onto the doubly stochastic manifold using the Sinkhorn-Knopp algorithm. This algorithm iteratively normalizes the rows and columns of a positive matrix to sum to one, converging to a doubly stochastic matrix. The authors implement this projection as a custom kernel that performs the iterative normalization process.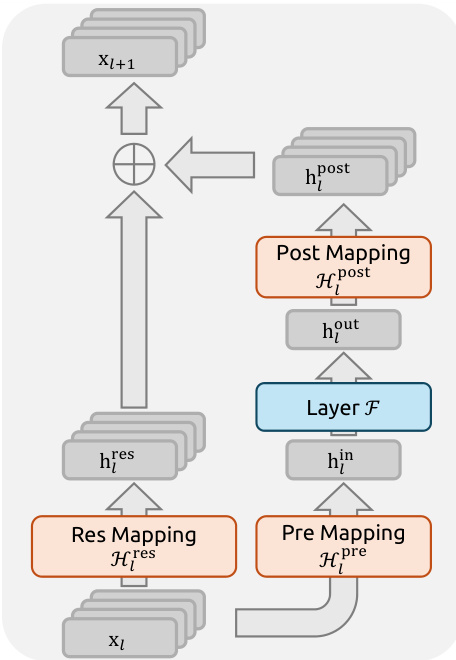

To ensure practical scalability, mHC incorporates a suite of infrastructure optimizations. The authors employ kernel fusion to reduce memory bandwidth bottlenecks and improve computational efficiency. They fuse multiple operations with shared memory access into unified compute kernels, such as combining the two scans on the input vector $\vec{\mathbf{x}}_l$xl​ and the two matrix multiplications in the backward pass. They also implement a specialized kernel for the Sinkhorn-Knopp iteration and a custom backward kernel that recomputes intermediate results on-chip. To mitigate the substantial memory overhead introduced by the $n$n-stream residual design, the authors use selective recomputing. They discard intermediate activations after the forward pass and recompute them on-the-fly during the backward pass. This is done for blocks of $L_r$Lr​ consecutive layers, and the optimal block size is determined by minimizing the total memory footprint. Furthermore, to address communication latency in large-scale training, the authors extend the DualPipe schedule. They execute the $m$mHC kernels for MLP layers on a dedicated high-priority compute stream to prevent blocking the communication stream. This design allows for the preemption of overlapped attention computations and enables flexible scheduling, thereby improving the utilization of compute resources.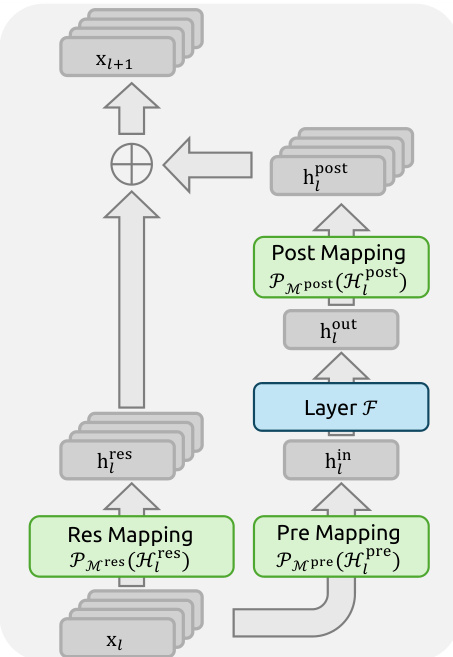

The communication-computation overlapping for mHC is illustrated in the DualPipe schedule. The schedule is designed to handle the overhead introduced by mHC, particularly the communication latency across pipeline stages and the computational overhead of recomputation. The figure shows the timeline for the normal compute stream, communication stream, and high-priority compute stream. The high-priority stream is used to execute the $m$mHC kernels for MLP layers, ensuring that they do not block the communication stream. The recomputation process is decoupled from pipeline communication dependencies, as the initial activation of each stage is already cached locally. This allows for improved overlapping of communication and computation at pipeline stage boundaries.

Experiment

• Numerical instability experiment: HC suffers from signal explosion due to unbounded composite residual mappings, with Amax Gain Magnitude peaking at 3000, leading to loss surges and unstable gradients in 27B models.
• System overhead experiment: HC incurs significant memory I/O and communication costs, increasing by a factor proportional to n, degrading training throughput and requiring gradient checkpointing.
• Main results: On the 27B model, $m$mHC achieves a 0.021 lower final loss than the baseline, with stable gradients and superior downstream performance, outperforming both baseline and HC across 8 benchmarks, including +2.1% on BBH and +2.3% on DROP.
• Scaling experiments: $m$mHC maintains consistent performance gains across compute and token scaling, with robust improvements from 3B to 27B models and stable within-run dynamics.
• Stability analysis: $m$mHC reduces the maximum Amax Gain Magnitude from ~3000 (HC) to ~1.6, ensuring bounded signal propagation and stable forward/backward flows, validated by visualized mappings.

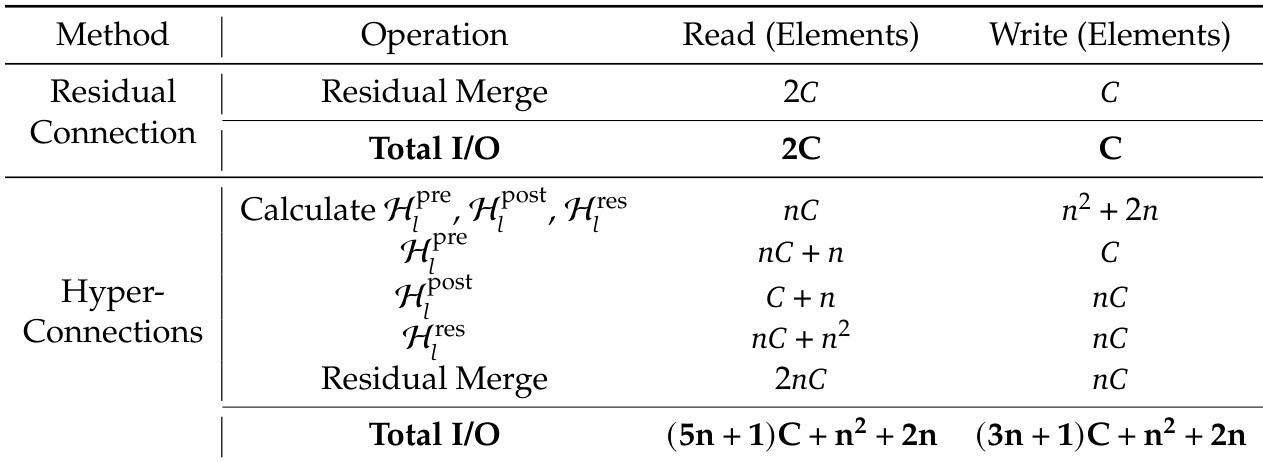
The authors use the table to detail the memory access patterns and storage requirements of the hyper-connection (HC) mechanism in a pre-norm Transformer architecture. Results show that HC increases memory access costs by a factor proportional to the number of residual streams, with activations stored every Lr layers for pre-activation inputs and transiently within Lr layers for post-activation inputs, leading to higher I/O demands and memory footprint.

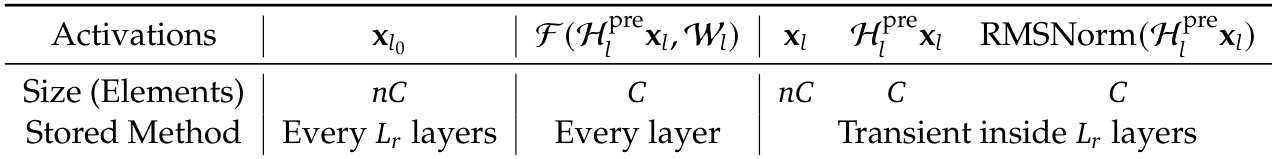
The authors use a 27B model to compare the performance of HC and mHC against a baseline across eight downstream benchmarks. Results show that mHC consistently outperforms both the baseline and HC, achieving higher scores on most tasks, including significant improvements of 2.1% on BBH and 2.3% on DROP.

The authors use the table to compare the propagation stability of HC and mHC by analyzing the gain magnitudes of their respective residual mappings. Results show that HC exhibits extreme signal amplification, with composite mapping gains reaching up to 3000, indicating severe instability. In contrast, mHC maintains bounded gains, with maximum values around 1.6, demonstrating significantly improved stability in both forward and backward signal propagation.

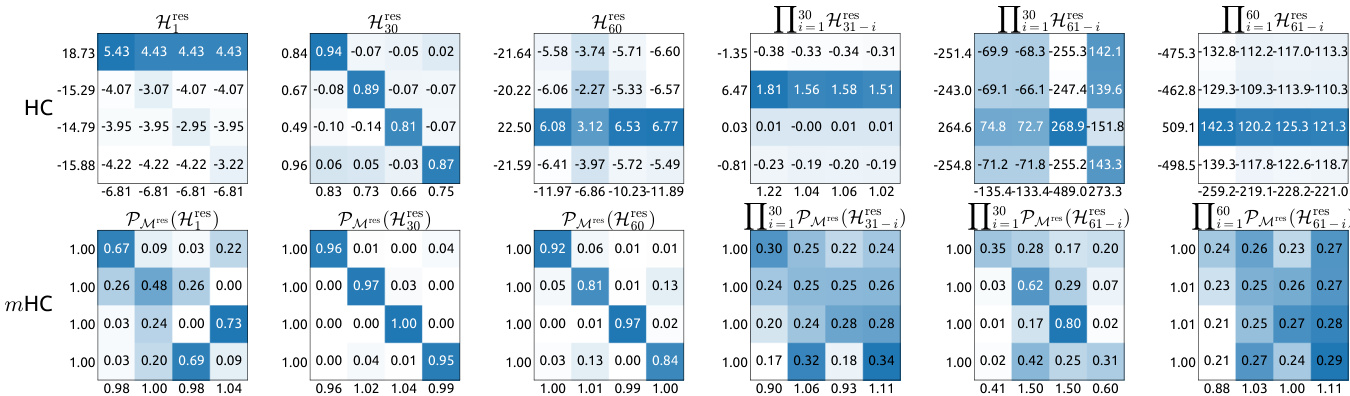
The authors use a table to compare the impact of different residual mapping components on training stability, showing that adding pre- and post-norm mappings alongside the residual mapping reduces the absolute loss gap. Results show that the combination of all three mappings achieves the lowest loss gap of -0.027, indicating improved stability compared to configurations with fewer components.

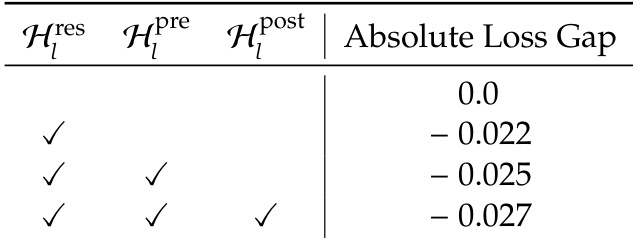
The authors use the table to quantify the memory access overhead introduced by Hyper-Connections (HC) compared to standard residual connections. Results show that HC significantly increases both read and write operations, with total I/O scaling quadratically with the expansion rate n, leading to a substantial rise in system-level overhead. This increased I/O cost, particularly the quadratic growth in writes, contributes to degraded training throughput and higher memory usage, highlighting a key limitation of HC in large-scale models.