One-sentence Summary

The authors, affiliated with DeepSeek-AI, propose DeepSeek-Prover-V2, a 671B-parameter open-source model for formal theorem proving in Lean 4, which integrates informal and formal reasoning via a recursive pipeline leveraging DeepSeek-V3; it achieves state-of-the-art performance with an 88.9% pass rate on MiniF2F-test and solves 6 of 15 AIME problems, demonstrating a significant narrowing of the gap between natural-language and formal mathematical reasoning.

Key Contributions

• The paper addresses the challenge of bridging informal mathematical reasoning in large language models with the rigorous demands of formal theorem proving in Lean 4, by introducing a recursive theorem proving pipeline that uses DeepSeek-V3 to generate both natural-language proof sketches and formalized subgoals, enabling a unified framework for integrating informal and formal reasoning.

• The proposed DeepSeek-Prover-V2-671B model is trained via a cold-start procedure that combines DeepSeek-V3’s chain-of-thought reasoning with formally verified proofs of decomposed subgoals, followed by reinforcement learning, resulting in state-of-the-art performance on MiniF2F-test (88.9% pass ratio with Pass@8192) and 47 solved problems on PutnamBench.

• The authors introduce ProverBench, a new benchmark of 325 formalized problems including 15 from the AIME competitions (2024–2025), where DeepSeek-Prover-V2-671B successfully solves 6 of them—demonstrating a significant narrowing of the gap between formal and informal mathematical reasoning in LLMs.

Introduction

The authors address the challenge of bridging informal mathematical reasoning in large language models (LLMs) with the syntactic rigor required for formal theorem proving in systems like Lean. While LLMs excel at natural language chain-of-thought reasoning, their heuristic-driven, approximate style lacks the precision needed for formal verification, where every step must be explicitly justified. Prior approaches attempted to close this gap using proof sketches to guide formal proof construction, but struggled with sparse training signals and inefficient proof search. To overcome these limitations, the authors introduce DeepSeek-Prover-V2, which leverages a two-stage pipeline: first, a large general-purpose model (DeepSeek-V3) generates high-level proof sketches and recursively decomposes complex theorems into subgoals formalized in Lean, with intermediate steps left as sorry placeholders; second, a smaller 7B prover model resolves these subgoals recursively, enabling efficient proof search. The authors further enhance training by constructing a curriculum of increasingly difficult conjectures derived from subgoals, creating dense, high-quality training data. This cold-start data is then refined via reinforcement learning, significantly improving the model’s ability to solve formal proofs. The resulting DeepSeek-Prover-V2-671B achieves state-of-the-art performance on benchmarks including MiniF2F, ProofNet, and PutnamBench, and successfully solves challenging AIME problems, demonstrating strong generalization and reasoning capabilities.

Dataset

• The dataset, named ProverBench, consists of 325 formalized mathematical problems, combining 15 problems from the AIME 24&25 competition and 310 problems drawn from curated high school and undergraduate textbooks.
• The AIME subset includes only number theory and algebra problems, selected to avoid geometry, combinatorics, and counting problems with complex Lean representations; this results in 15 clean, competition-level formalizations.
• The textbook subset spans a broad range of mathematical domains, including number theory, algebra, linear algebra, abstract algebra, calculus, real and complex analysis, functional analysis, and probability, covering both high-school competition and undergraduate-level content.
• The dataset is designed to support evaluation across informal reasoning (e.g., AIME) and formal proof generation (e.g., textbook problems), enabling a direct comparison of model performance in different reasoning modes.
• The authors use ProverBench to evaluate DeepSeek-Prover-V2-671B in a formal proof generation setting, where the model must construct valid Lean 4 proofs from given correct answers.
• For the AIME problems, the model is evaluated using a find-answer task with majority voting over 16 sampled responses, while for textbook problems, it is assessed on its ability to generate correct formal proofs.
• The dataset is processed to ensure compatibility with Lean 4.9.0, with problematic or misformulated statements excluded during evaluation.
• The authors also leverage a public synthetic dataset from Dong and Ma (2025) for supervised fine-tuning, which includes variants of ProofNet-valid problems, while the original ProofNet-test split is reserved exclusively for final model evaluation.
• The model is trained using a mixture of data sources, including high-school level problems and college-level formalizations, enabling strong generalization to advanced mathematical domains.
• During training, the model is exposed to CoT (Chain-of-Thought) reasoning, which significantly improves pass rates on both ProofNet-test and PutnamBench compared to non-CoT settings.
• A cropping strategy is applied to exclude problems incompatible with Lean 4.9.0, particularly in PutnamBench, where two problems were removed due to misformulated statements after initial evaluation.
• Metadata for each problem includes topic classification, difficulty level, and source (AIME or textbook), enabling detailed analysis of model performance across domains and reasoning styles.

Method

The model architecture of DeepSeek-Prover-V2 is designed around a two-stage training pipeline that integrates both informal mathematical reasoning and formal proof construction, enabling the synthesis of high-quality training data through a recursive theorem-proving framework. The overall approach leverages DeepSeek-V3 as a high-level reasoning engine to decompose complex problems into manageable subgoals, which are then resolved by a smaller 7B prover model. This decomposition process is formalized into a structured chain-of-thought, where the intermediate reasoning steps from DeepSeek-V3 are combined with the formal proofs generated by the 7B model to create a cohesive, unified dataset. The resulting cold-start data, which includes both informal reasoning and formal proof steps, serves as the foundation for training the larger DeepSeek-Prover-V2-671B model.

The training process begins with a cold-start phase that generates synthetic data by recursively decomposing challenging problems. The authors use DeepSeek-V3 to decompose a problem into a sequence of subgoals, and then synthesize the formal proofs for these subgoals using the 7B prover model. The proofs of the resolved subgoals are then composed into a complete formal proof for the original problem. This complete proof is appended to DeepSeek-V3's chain-of-thought reasoning, which outlines the lemma decomposition, creating a unified dataset that bridges informal and formal reasoning. This synthetic data is used to initialize the model, providing a strong starting point for further refinement.

The two-stage training pipeline consists of a supervised fine-tuning (SFT) stage followed by a reinforcement learning (RL) stage. The first stage employs expert iteration within a curriculum learning framework to train a non-Chain-of-Thought (non-CoT) prover model. This model is optimized for rapid generation of formal Lean code without explicit intermediate reasoning steps, which accelerates the iterative training and data collection process. The training corpus for this stage is composed of non-CoT data collected through expert iteration, which produces concise Lean codes, and the cold-start CoT data synthesized from DeepSeek-V3's reasoning patterns. The non-CoT data emphasizes formal verification skills, while the CoT data explicitly models the cognitive process of transforming mathematical intuition into formal proof structures.

The second stage enhances the model's ability to bridge informal reasoning with formal proof construction through a reinforcement learning stage. The authors use Group Relative Policy Optimization (GRPO) as the training algorithm, which eliminates the need for a separate critic model by sampling a group of candidate proofs for each theorem prompt and optimizing the policy based on their relative rewards. The training utilizes binary rewards, where each generated Lean proof receives a reward of 1 if verified as correct and 0 otherwise. To ensure effective learning, the training prompts are curated to include only problems that are sufficiently challenging yet solvable by the supervised fine-tuned model. During each iteration, 256 distinct problems are sampled, and 32 candidate proofs are generated per theorem with a maximum sequence length of 32,768 tokens. This process allows the model to refine its reasoning and proof construction capabilities, leading to significant improvements in formal theorem proving.

Experiment

• Evaluated on CombiBench, DeepSeek-Prover-V2-671B solved 10 out of 77 problems in the with-solution setting, demonstrating generalization to combinatorial problems despite training focus on number theory and algebra; the model also showed ability to detect and adapt to misformulated problem statements.
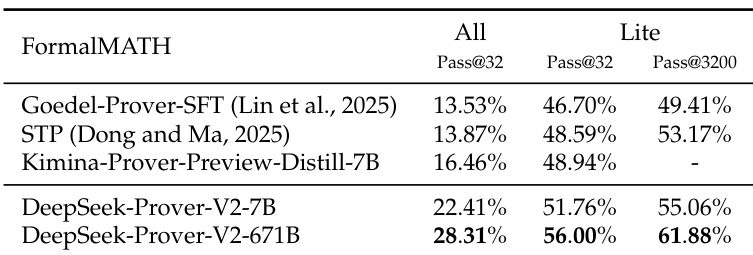
• On FormalMATH-Lite, DeepSeek-Prover-V2-671B achieved 56.00% success rate with 32 samples and improved to 61.88% with 3200 samples, outperforming prior models including Goedel-Prover-SFT, STP, and Kimina-Prover-Preview-Distill-7B; on the full FormalMATH-All dataset, it solved 28.31% of problems.
• On ProverBench, DeepSeek-Prover-V2-671B achieved strong results on both the full set (325 problems) and the AIME 24&25 subset, demonstrating competitive performance against state-of-the-art provers.

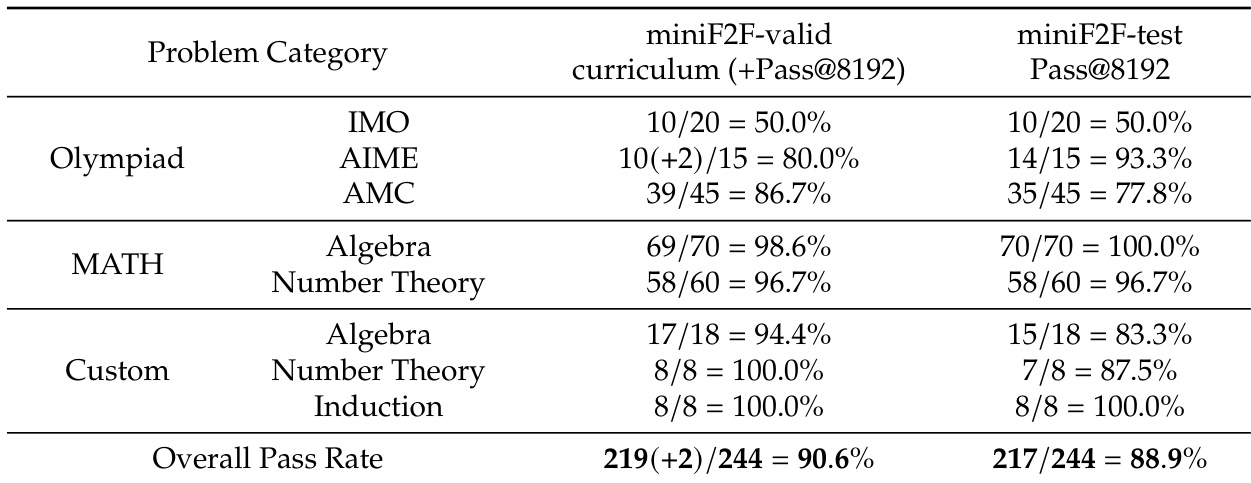
The authors use the miniF2F benchmark to evaluate DeepSeek-Prover-V2 on formal theorem proving tasks, reporting pass rates across different problem categories and datasets. Results show that the model achieves a high overall pass rate of 90.6% on the miniF2F-valid curriculum and 88.9% on the miniF2F-test set, with particularly strong performance in algebra and number theory problems.

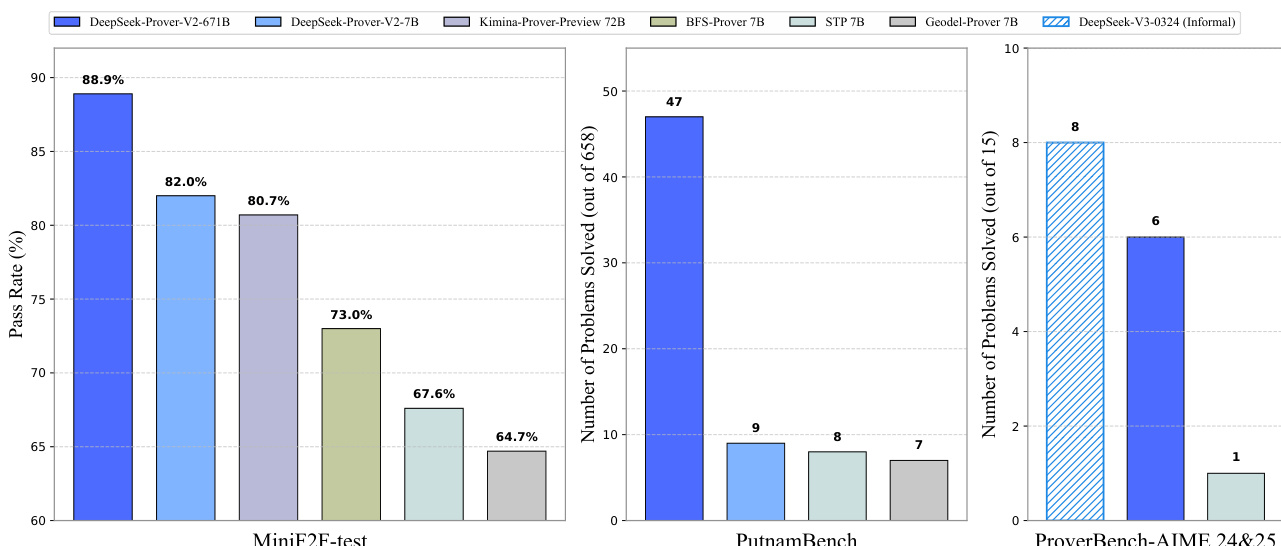
The authors use DeepSeek-Prover-V2-671B to evaluate performance on MiniF2F-test, PutnamBench, and ProverBench-AIME 24&25, showing pass rates of 88.9%, 82.0%, and 80.7% respectively on MiniF2F-test, solving 47 out of 658 problems on PutnamBench, and achieving 8 out of 15 on ProverBench-AIME 24&25. Results show that DeepSeek-Prover-V2-671B outperforms other models across all benchmarks, with the largest gap observed on MiniF2F-test where it achieves a 6.9 percentage point lead over the second-best model.

Results show that DeepSeek-Prover-V2-671B achieves the highest performance on FormalMATH-Lite, solving 61.88% of problems with 3200 samples, outperforming all baselines. On the full FormalMATH dataset, it solves 28.31% of problems with 32 samples, demonstrating strong effectiveness compared to other models.

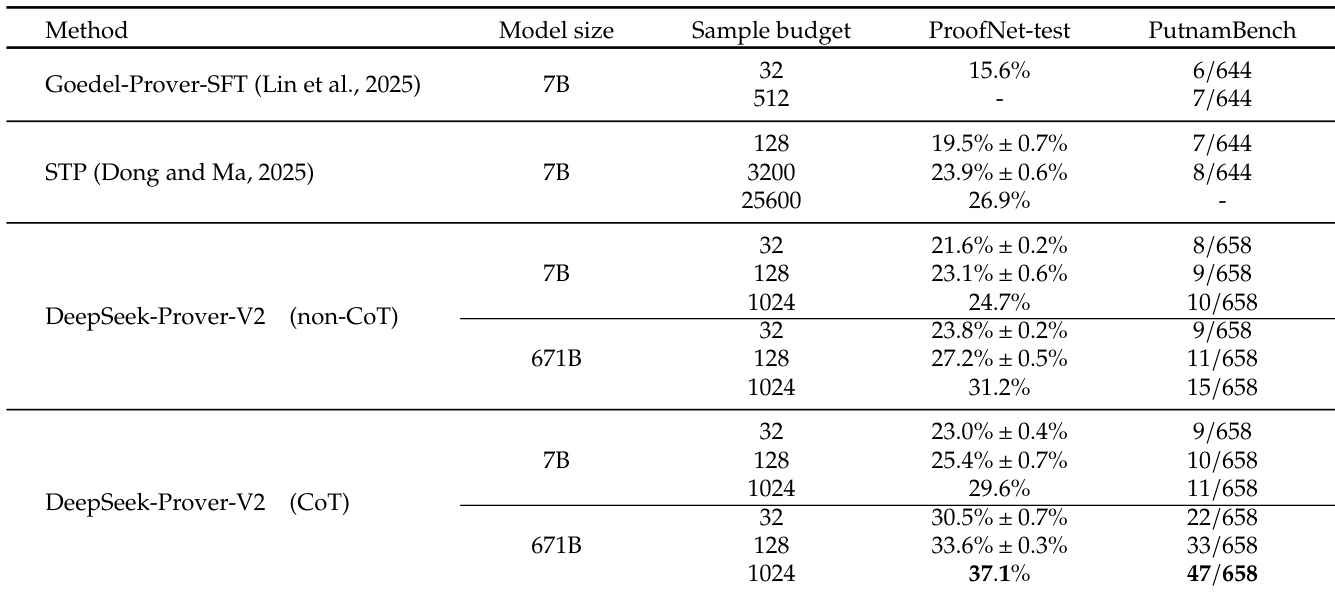
The authors use the provided table to compare the performance of DeepSeek-Prover-V2-7B and DeepSeek-Prover-V2-671B under non-CoT and CoT generation modes, with the number of output tokens set to 7B and 671B respectively. Results show that the CoT mode significantly improves performance for both model sizes, with the 671B model achieving the highest score of 6751.9 in the CoT setting.

Results show that DeepSeek-Prover-V2 achieves strong performance across multiple benchmarks, with the 671B model outperforming other methods in both ProofNet-test and PutnamBench. The CoT version of DeepSeek-Prover-V2 significantly improves results, particularly on PutnamBench, where the 671B model reaches 47/658, demonstrating the effectiveness of chain-of-thought reasoning.