Command Palette
Search for a command to run...
Le MIT Développe SCIGEN, Une Conception Ciblée Pour Les Matériaux Stables, Qui Peut s'adapter À n'importe Quel Modèle De Diffusion pré-entraîné.
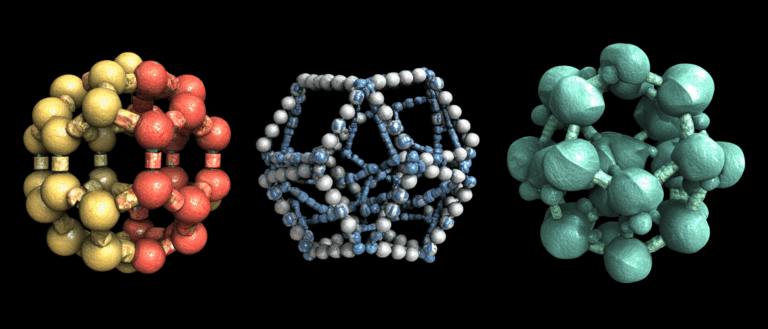
En science des matériaux, les propriétés quantiques des matériaux (telles que l'isolation topologique, la supraconductivité et l'ordre magnétique) n'existent pas isolément, mais sont directement déterminées par des propriétés structurelles telles que la symétrie de leur arrangement atomique et la géométrie de leur réseau. Ceci fournit une base théorique pour la conception ciblée de matériaux quantiques par manipulation structurale. Cependant, passer de la « possibilité théorique » à l'« utilisabilité pratique » n'est pas chose aisée. En raison de facteurs pratiques tels que la complexité de la manipulation structurale et la rareté des données pertinentes, les progrès dans la conception de matériaux stables aux propriétés quantiques idéales ont été lents. Par exemple, après une décennie de recherche, seule une douzaine de matériaux candidats pour les liquides de spin quantiques ont été identifiés.
Le changement de paradigme scientifique induit par l'intelligence artificielle transforme les méthodes et les approches de conception des matériaux. Par exemple, les principaux modèles de génération de matériaux tels que CDVAE, UniMat, DiffCSP et GNoME (principalement basés sur des modèles de diffusion ou des architectures de réseaux neuronaux graphes) ont démontré un potentiel considérable pour identifier des structures cristallines stables et générer par lots des millions de matériaux candidats.Cependant, la plupart des méthodes s’appuient encore sur l’échantillonnage à partir de la distribution statistique des données de formation, ce qui fait que les matériaux de sortie sont limités aux types courants dans les bases de données existantes en termes de topologie structurelle et de caractéristiques de performance.Cependant, les groupes d'espace cristallographiques ne fournissent qu'un cadre structural macroscopique pour un matériau, sans capturer les motifs géométriques locaux cruciaux. Par conséquent, le développement de méthodes d'apprentissage automatique capables d'intégrer précisément les contraintes de motifs géométriques spécifiques est essentiel pour surmonter les obstacles liés aux matériaux connus et explorer de nouveaux phénomènes quantiques.
Observer les difficultés dans la recherche et le développement des matériaux quantiques,L'équipe du professeur Mingda Li au MIT, en collaboration avec l'Université d'État du Michigan, le laboratoire national d'Oak Ridge et d'autres, a proposé une méthode d'intégration de contraintes structurelles géométriques appelée SCIGEN (Structural Constraint Integration in a GENerative model).Cette méthode peut être adaptée à tout modèle de diffusion générative pré-entraîné afin d'intégrer des contraintes de symétrie et de motifs géométriques, générant ainsi des matériaux cibles avec des contraintes spécifiques. Un avantage clé de cette méthode est qu'elle élimine le besoin de ré-entraîner ou d'affiner le modèle sous-jacent, augmentant ainsi considérablement la flexibilité et la polyvalence du cadre et permettant une adaptation rapide à différents modèles de diffusion pré-entraînés, améliorant ainsi l'efficacité et la rapidité.
La recherche connexe a été publiée dans la revue de référence Nature Materials sous le titre « Intégration de contraintes structurelles dans un modèle génératif pour la découverte de matériaux quantiques ».
Points saillants de la recherche :
* L'étude propose une solution pour adapter tout modèle génératif de diffusion pré-entraîné sans réentraîner ni affiner le modèle de base, brisant ainsi la dépendance traditionnelle du modèle génératif de contraintes à l'égard de l'entraînement secondaire du modèle de base.
* La méthode proposée par l'institut a favorisé le changement de paradigme de la découverte de matériaux quantiques, de la « méthode des essais et erreurs » à la « génération dirigée », accélérant ainsi le développement des matériaux quantiques.
* L'étude a synthétisé et caractérisé deux matériaux prédits, TiPd₀.₂₂Bi₀.₈₈ et Ti₀.₅Pd₁.₅Sb, qui présentent respectivement un paramagnétisme et un diamagnétisme

Adresse du document :
https://www.nature.com/articles/s41563-025-02355-y
Suivez le compte public et répondez à «SCIGEN Obtenez le PDF complet
Autres articles sur les frontières de l'IA :
Support de données : Construction et criblage d'une base de données de matériaux à réseau archimédien à grande échelle
Dans cette étude, les chercheurs ont utilisé SCIGEN pour compiler une base de données complète de matériaux AL (réseaux d'Archimède) pour l'exploration expérimentale.
L'ensemble de données contient un total de 10,06 millions de matériaux avec AL.Après un pré-criblage de stabilité en quatre étapes, les chercheurs ont retenu plus de 1,01 million de matériaux. Ils ont ensuite effectué des calculs de relaxation structurale DFT (théorie de la fonctionnelle de la densité) à haut débit sur 26 000 matériaux prioritaires, faisant converger 24 743 matériaux. Plus de 951 structures TP3T ont convergé et plus de 531 matériaux TP3T ont atteint des minima d'énergie en 150 étapes d'optimisation structurale.
Pour identifier la structure magnétique, les chercheurs ont ensuite utilisé un modèle de classification basé sur un réseau neuronal graphique pour l'identifier, où la structure optimisée DFT de 41% a été identifiée comme magnétique.
Enfin, après le criblage des données matérielles,Les chercheurs ont également synthétisé deux nouveaux matériaux : TiPd₀.₂₂Bi₀.₈₈ et Ti₀.₅Pd₁.₅Sb.
Analyse du modèle : perfectionner la logique de conception et améliorer les capacités du modèle de génération de matériaux
SCIGEN intègre les contraintes géométriques directement au processus de génération par diffusion, permettant ainsi aux modèles de génération de matériaux d'explorer plus efficacement les matériaux quantiques stables présentant la géométrie et les propriétés quantiques souhaitées. Grâce à une chaîne logique « guidage par contrainte-itération par masque-convergence de débruitage », partant de la contrainte cible, des structures contraintes aléatoires sont diffusées sur plusieurs pas de temps. Avant chaque diffusion, la structure contrainte masque la structure débruitée, créant un biais inductif qui guide le processus de génération vers un résultat conforme aux contraintes. L'application itérative du masquage à chaque étape de débruitage permet de faire converger de manière déterministe tous les atomes du masque vers des positions correspondant à toutes les structures géométriques imposées. SCIGEN garantit ainsi que les matériaux générés respectent les contraintes géométriques prédéfinies tout en préservant la validité générative du modèle sous-jacent.
Plus précisément, l’objectif de la génération de structures cristallines est de trouver un cristal périodique M, qui peut être composé de trois composants,Français Il s'agit de : une matrice de réseau L = [l₁, l₂, l₃] ∈ R³ᕽ³, contenant trois vecteurs de base, décrivant la structure spatiale globale du cristal ; des coordonnées fractionnaires F = [f₁, f₂, …, f៷] ∈ [0, 1)³ᕽᴺ, représentant les positions relatives des atomes dans le réseau (limitées à la plage [0, 1) pour refléter la périodicité) ; et un codage de type d'atome one-hot A = [a₁, a₂, …, a៷] ∈ [0, 1)ʰᕽᴺ, qui utilise un code binaire pour identifier le type spécifique de chaque atome. Lors de la génération de matériaux par diffusion, SCIGEN applique des contraintes géométriques à L, F et A pour garantir que la structure générée est conforme à la morphologie cible.
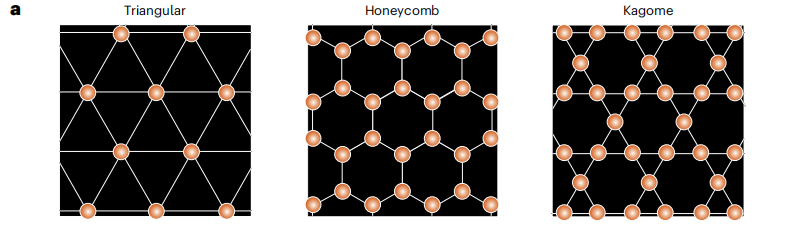
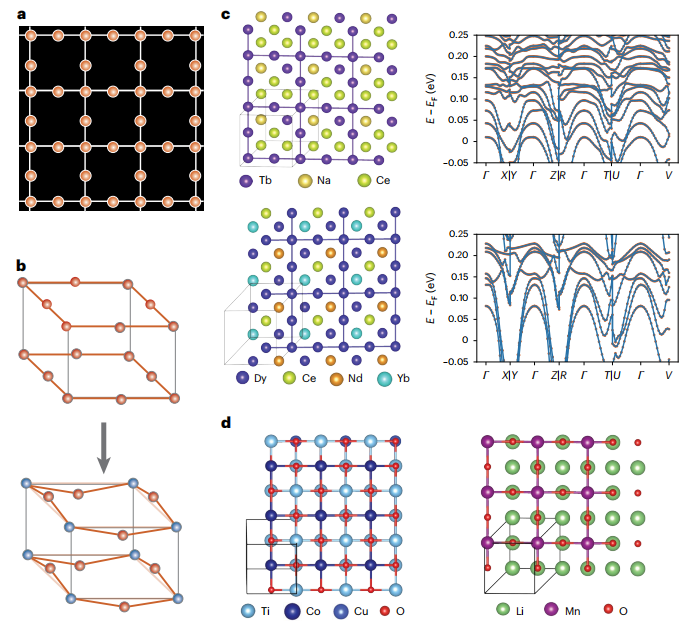
Comme le montre la figure a ci-dessous,Les réseaux représentatifs que SCIGEN peut contraindre comprennent les réseaux triangulaires, les réseaux en nid d'abeille et les réseaux Kagome.Il s’agit des structures centrales qui hébergent des phénomènes quantiques uniques tels que les liquides de spin quantiques.
La figure b ci-dessous illustre le processus d'initialisation d'une structure contrainte. Les règles fondamentales d'initialisation des structures contraintes reposent sur un « réseau d'Archimède composé d'atomes magnétiques », garantissant que la structure contrainte possède d'emblée des propriétés quantiques potentielles. La figure c illustre l'algorithme de génération des composants de contrainte intégrés, présentant visuellement le processus complet de « diffusion de la structure contrainte – initialisation de la structure non contrainte – fusion des deux – débruitage itératif ».
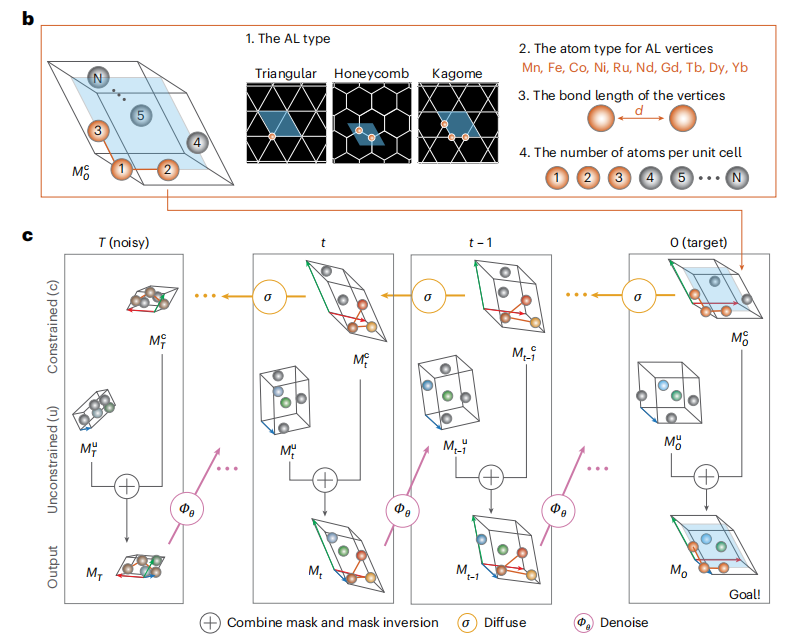
Parmi eux, le cœur de SCIGEN, de l'initialisation à la génération de la structure finale M₀, est « l'intégration itérative de composants contraints et non contraints ».Tout d'abord, la structure de contrainte initialisée (telle que AL composée d'atomes magnétiques) est soumise à un ajout de bruit pendant T = 1000 étapes pour obtenir la structure de contrainte Mᶜₜ (t∈[1, T]) à chaque pas de temps.Cette étape fournit un « chemin prédéfini » pour débruiter les composants contraints, empêchant ainsi toute génération ultérieure de s'écarter de la géométrie cible. La structure non contrainte est initialement constituée d'une structure Mᵘₜ complètement bruitée, représentant la partie du processus de génération librement optimisable. Ces deux structures sont ensuite intégrées pour former la structure composite MT, qui est ensuite débruitée pour produire Mᵘₜ₋₁. Cette logique est répétée à toutes les étapes suivantes, guidant finalement certains atomes vers la formation de la structure plane AL par itération, aboutissant à la structure cristalline cible M₀.
Pour prouver l'efficacité des contraintes SCIGEN,L’étude a également prouvé, à la fois par des preuves mathématiques et par des vérifications informatiques, que SCIGEN ne détruit pas la distribution originale du modèle sous-jacent lors de l’imposition de contraintes.Après avoir généré un grand nombre de matériaux, la stabilité est évaluée par « pré-criblage en quatre étapes + relaxation DFT à haut débit » pour garantir que les candidats matériaux quantiques potentiellement stables sont éliminés.
* Un processus de présélection en quatre étapes combine des règles chimiques qui vérifient la neutralité de la charge et le volume de la cellule unitaire occupée par les atomes avec un réseau neuronal auxiliaire qui prédit la stabilité en fonction de la valeur de l'énergie de l'enveloppe convexe Eₕᵤₗₗ (plus la valeur Eₕᵤₗₗ est faible, plus le matériau est thermodynamiquement stable).
* La relaxation DFT à haut débit effectue des calculs de théorie de la fonctionnelle de la densité sur les matériaux criblés. Grâce à la relaxation structurale (optimisation des positions atomiques et des dimensions des mailles unitaires), nous identifions des candidats potentiellement stables, fournissant ainsi une base pour des synthèses expérimentales ultérieures ou des recherches approfondies.
Vérification expérimentale : SCIGEN démontre des capacités exceptionnelles de génération directionnelle et de prédiction des matériaux
Dans l'expérience spécifique, le modèle de base a adopté le modèle DiffCSP, qui a également vérifié la conservation des capacités du modèle de génération de base.
d'abord,Les expériences montrent les résultats de la génération de matériaux sous trois contraintes AL principales :La capacité de génération directionnelle de SCIGEN est vérifiée sur la base du réseau triangulaire, du réseau en nid d'abeille et du réseau Kagome, comme illustré dans la figure ci-dessous.
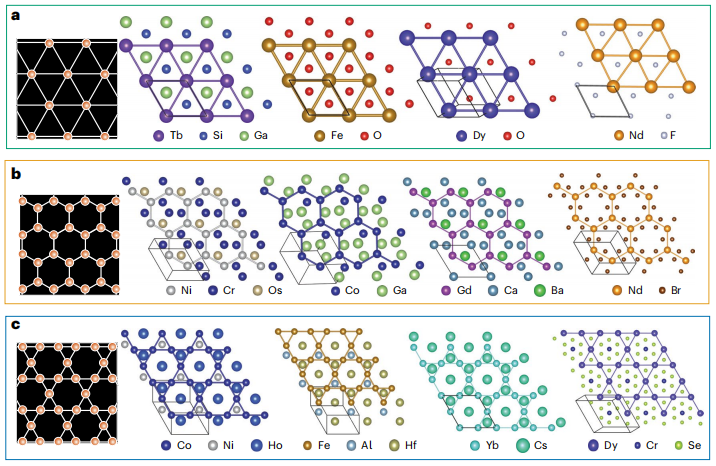
Les résultats montrent queSCIGEN peut guider avec précision les atomes contraints pour les organiser selon des motifs géométriques prédéfinis, et les contraintes n'agissent que sur les composants cibles.Les positions des atomes libres ne sont pas strictement définies, ce qui garantit un processus de génération dirigé et flexible. Leur position est naturellement déterminée au cours du processus, sous l'influence de facteurs spatiaux et de liaison. Pour les réseaux triangulaires, les atomes libres tendent à occuper des positions reliant trois atomes magnétiques, formant ainsi des triangles équilatéraux. Pour les réseaux en nid d'abeille, les atomes libres apparaissent généralement au centre d'hexagones formés par des atomes magnétiques, coplanaires aux plans du réseau. Pour les réseaux de Kagome, les atomes libres relient les triangles équilatéraux et les hexagones de chaque couche du réseau de Kagome. Si l'espace interne du polygone du réseau est trop étroit, ils seront décalés hors du plan AL. Pour les polygones plus grands, comme les hexagones, ils peuvent être disposés coplanairement avec les atomes libres.
Pour générer des structures de matériaux confinés présentant une probabilité de stabilité plus élevée, les chercheurs ont également conçu un schéma d'échantillonnage des conditions initiales en analysant les taux de survie après criblage. L'objectif est de déterminer le choix optimal du « nombre d'atomes par cellule unitaire (N) » et du « type d'atomes magnétiques aux sommets de l'AL ». Les chercheurs ont d'abord échantillonné les valeurs N selon une distribution uniforme et calculé les « taux de survie après criblage multi-étapes » correspondants pour différentes valeurs N afin d'obtenir une distribution de probabilité stable pour N. Sur la base de cette distribution, N a ensuite été échantillonné pour initialiser la génération à grande échelle : les réseaux triangulaires sont plus adaptés aux valeurs N faibles, tandis que les réseaux en nid d'abeille et Kagome sont plus adaptés aux valeurs N élevées. Ceci est illustré dans la figure d ci-dessous.
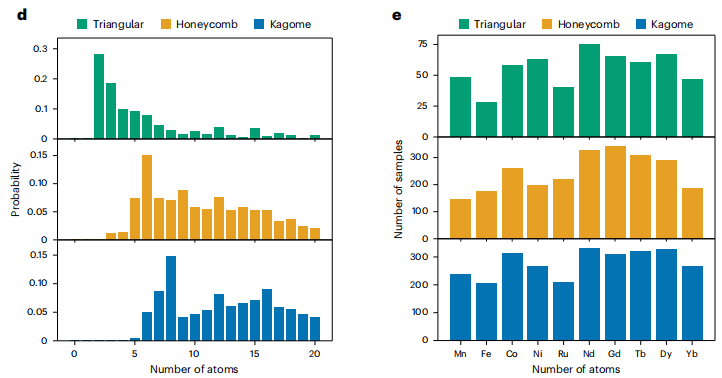
Figure e : Quantité de matière restante après le pré-criblage des types d’atomes magnétiques courants dans chaque motif géométrique majeur.
Comme le montre la figure e ci-dessus, 10 atomes magnétiques courants (Mn, Fe, Co, Ni, Ru, Nd, Gd, Tb, Dy, Yb) ont été testés expérimentalement.3 000 matériaux ont été générés pour chaque type de réseau et chaque atome magnétique, et le nombre de matériaux stables après pré-criblage a été compté.Les résultats montrent que, bien que la quantité de matériaux stables varie selon les atomes magnétiques, les dix types d'atomes magnétiques peuvent former des structures AL. Par conséquent, lors de leur génération à grande échelle, un échantillonnage à probabilité égale est utilisé pour les types d'atomes de vertex AL afin de prendre en compte à la fois la diversité et la stabilité.
Outre les trois principaux réseaux mentionnés ci-dessus, SCIGEN peut également être appliqué à d'autres réseaux d'Archimède, tels que les carrés, les triangles allongés et les carrés tronqués, soit sept types de matériaux contraints par la loi d'espace. Les atomes libres jouent également un rôle clé dans ces réseaux, comblant les espaces entre les couches du réseau et améliorant ainsi la stabilité mécanique et thermique de la structure. Ils peuvent même former spontanément des motifs de loi d'espace reconnaissables, suggérant que les structures de loi d'espace ont une « préférence de stabilité fixe » en coordonnées locales, ouvrant ainsi la voie à l'exploration de matériaux quantiques plus singuliers. (Voir la figure ci-dessous.)

En tant que variante du carré AL,Les chercheurs ont également démontré expérimentalement la percée de SCIGEN dans la génération de matériaux en réseau de Lieb.Les résultats montrent que SCIGEN peut générer des matériaux stables de type Lieb grâce à des contraintes géométriques, validant ainsi sa capacité à générer des structures de réseau rares. Dans ces matériaux de type Lieb, les atomes magnétiques tels que Tb et Dy sont orientés aux nœuds du réseau de Lieb, jetant ainsi les bases des études de propriétés magnétiques. Des calculs de relaxation structurale DFT ultérieurs sur les matériaux générés ont révélé que l'architecture globale du réseau de Lieb demeure intacte. D'autres calculs de bande ont révélé que ces matériaux présentent les caractéristiques de bande plate électroniques attendues près du niveau de Fermi, confirmant ainsi que les matériaux générés par SCIGEN sont non seulement structurellement stables, mais présentent également le comportement électronique quantique unique du réseau de Lieb. Ceci est illustré dans la figure ci-dessous.
Pour faire évoluer les matériaux de réseau de type Lieb vers des analogues d'oxyde de matériaux supraconducteurs pratiques, SCIGEN a introduit une stratégie de « démasquage adaptatif » qui équilibre la rigidité des contraintes et la flexibilité structurelle, créant ainsi un pont entre la recherche fondamentale sur les réseaux de Lieb et l'exploration des applications supraconductrices.
Pour vérifier la capacité prédictive et l'efficacité de SCIGEN,Les chercheurs ont synthétisé et testé deux composés complètement nouveaux : TiPd₀.₂₂Bi₀.₈₈ et Ti₀.₅Pd₁.₅Sb.Les expériences montrent que, malgré de légères différences de stœchiométrie et de symétrie cristalline par rapport à leurs homologues prédits par SCIGEN, les résultats expérimentaux restent très cohérents avec les résultats calculés. Le premier présente un paramagnétisme et le second un diamagnétisme.Cela démontre la capacité de SCIGEN à proposer des motifs structurels chimiquement plausibles, qui, bien que n'étant pas sous une forme idéalisée, peuvent néanmoins fournir une base et une valeur pour une exploration plus approfondie.
En résumé, SCIGEN, en tant que cadre innovant basé sur l’apprentissage automatique général, ouvre des domaines auparavant inaccessibles dans l’espace de conception des matériaux, ouvrant la voie à des percées dans les matériaux quantiques basées sur la relation entre la structure et les performances.
La découverte de matériaux quantiques et l'intelligence artificielle entrent en collision pour créer un feu d'artifice brillant
La relation structure-performance est devenue un concept central de la recherche et du développement de nouveaux matériaux. Elle présente deux avantages majeurs : premièrement, comprendre les phénomènes quantiques fonctionnels des matériaux grâce à la structure ; deuxièmement, prédire la microstructure du matériau grâce à ses performances ; et enfin, grâce à la manipulation de la structure, permettre la conception ciblée de matériaux cibles. Le développement de l’intelligence artificielle ouvre sans aucun doute une nouvelle voie pour l’étude systématique de la relation entre ces deux aspects, offrant ainsi de nouvelles possibilités d’accélération de la recherche et du développement de nouveaux matériaux.
Outre les réalisations mentionnées ci-dessus, la communauté de recherche scientifique a une longue histoire d’étude de la relation structure-performance, comme la recherche sur le modèle de base mentionné dans l’article.Parmi eux, l'équipe Google DeepMind a publié une étude intitulée « Scaling deep learning for materials discovery ».Une méthode appelée GNoME (réseaux de graphes pour l'exploration des matériaux) est proposée pour réaliser une extension de l'apprentissage automatique de l'exploration des matériaux grâce à un apprentissage actif à grande échelle.
La méthode repose sur deux éléments clés : premièrement, la mise en place de méthodes permettant de générer diverses structures candidates, telles que la substitution partielle sensible à la symétrie (SAPS) et la recherche de structures aléatoires ; deuxièmement, l’utilisation de réseaux neuronaux graphiques avancés (GNN) pour prédire l’énergie cristalline totale. Dans un processus itératif, le modèle GNoME utilise les données existantes pour entraîner et filtrer les structures candidates. Les calculs d’énergie DFT vérifient les prédictions et fournissent des données pour la phase d’entraînement suivante. Au final, plus de 2,2 millions de structures stables ont été découvertes.L'enveloppe convexe mise à jour contient 381 000 nouvelles entrées.Le nombre de cristaux stables a été augmenté d’un ordre de grandeur par rapport à avant.
Adresse du document :
https://www.nature.com/articles/s41586-023-06735-9
Le modèle sous-jacent utilisé dans les expériences susmentionnées provient d'une étude intitulée « Prédiction de la structure cristalline par diffusion équivariante conjointe », menée par des équipes de l'Université Tsinghua, de l'Université Renmin de Chine et de l'Université Sun Yat-sen.L’étude a proposé une méthode appelée DiffCSP pour résoudre le problème difficile de la prédiction de la structure cristalline.Le modèle est conçu sur la base d'un modèle de débruitage équivariant périodique et génère conjointement les coordonnées du réseau et atomiques de chaque cristal, ce qui peut mieux modéliser la géométrie du cristal.
Adresse du document :
https://arxiv.org/abs/2309.04475
En résumé, la méthode SCIGEN est une innovation fondée sur des résultats antérieurs. Elle affine le modèle de diffusion fondamental grâce à l'« intégration contrainte », ouvre une voie nouvelle, ciblée et efficace pour la découverte de matériaux quantiques et favorise la recherche et le développement de matériaux quantiques, de la méthode des « essais-erreurs à grande échelle » à la « conception dirigée ». Sa polyvalence pose également les bases de l'exploration ultérieure de matériaux aux structures et propriétés quantiques inconnues.