Sigmoid Function
Sigmoid functionIt is a common S-shaped function, also known as the S-shaped growth curve. Due to its monotonic increasing and inverse monotonic increasing properties, the Sigmoid function is often used as a threshold function of a neural network to map variables between 0 and 1.
Sigmoid function basic properties
The Sigmoid function form and image are as follows:
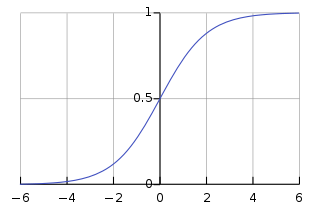
- Domain: ( −∞ , +∞ )
- Range: (− 1 , 1 );
- The function is a continuous smooth function within the domain of definition;
- It is differentiable everywhere, and its derivative is: f′ ( x ) = f ( x ) ( 1 − f ( x ) );
- The function takes values between 0 and 1, is centrally symmetric at 0.5, and has a greater slope as it approaches x = 0.
Sigmoid function and logistic regression
According to the purpose of logistic regression LR, the following two conditions must be met when selecting the function:
1) The value range is between 0 and 1;
2) For an event occurrence, 50% is the watershed of the result, and the selection function should be symmetric around 0.5.
Based on these two points, Sigmoid just meets the needs of LR.