ROOT: Robust Orthogonalized Optimizer for Neural Network Training
Wei He Kai Han Hang Zhou Hanting Chen Zhicheng Liu Xinghao Chen Yunhe Wang

Abstract
The optimization of large language models (LLMs) remains a critical challenge, particularly as model scaling exacerbates sensitivity to algorithmic imprecision and training instability. Recent advances in optimizers have improved convergence efficiency through momentum orthogonalization, but suffer from two key robustness limitations: dimensional fragility in orthogonalization precision and vulnerability to outlier-induced noise. To address these robustness challenges, we introduce ROOT, a Robust Orthogonalized Optimizer that enhances training stability through dual robustness mechanisms. First, we develop a dimension-robust orthogonalization scheme using adaptive Newton iterations with fine-grained coefficients tailored to specific matrix sizes, ensuring consistent precision across diverse architectural configurations. Second, we introduce an optimization-robust framework via proximal optimization that suppresses outlier noise while preserving meaningful gradient directions. Extensive experiments demonstrate that ROOT achieves significantly improved robustness, with faster convergence and superior final performance compared to both Muon and Adam-based optimizers, particularly in noisy and non-convex scenarios. Our work establishes a new paradigm for developing robust and precise optimizers capable of handling the complexities of modern large-scale model training. The code will be available at https://github.com/huawei-noah/noah-research/tree/master/ROOT.
Code Repositories
Summarization
Researchers from Huawei Noah's Ark Lab introduce ROOT, a robust orthogonalized optimizer for large language models that enhances training stability and convergence speed by employing adaptive Newton iterations and proximal optimization to overcome the dimensional fragility and noise sensitivity of existing momentum orthogonalization methods.
Introduction
The escalating computational demands of pre-training Large Language Models (LLMs) require optimizers that are both efficient and stable at scale. While standard methods like AdamW and newer matrix-aware approaches like Muon have advanced the field, they often struggle with numerical instability and precision gaps. Specifically, existing orthogonalization-based optimizers rely on fixed-coefficient approximations that fail to adapt to varying matrix dimensions, and they remain sensitive to gradient noise from outlier data samples which can corrupt update directions.
The authors introduce ROOT (Robust Orthogonalized Optimizer), a novel framework designed to enhance robustness against both structural uncertainties and data-level noise. By refining how weight matrices are orthogonalized and how gradients are filtered, ROOT ensures reliable training for massive neural networks without compromising computational efficiency.
Key innovations include:
- Adaptive Orthogonalization: The method employs a Newton-Schulz iteration with dimension-specific coefficients to ensure high precision across diverse network architectures, replacing imprecise fixed-coefficient schemes.
- Noise Suppression: A proximal optimization term utilizes soft-thresholding to actively mitigate the destabilizing effects of outlier-induced gradient noise.
- Enhanced Convergence: The approach achieves faster training speeds and superior performance in noisy, non-convex scenarios compared to current state-of-the-art optimizers.
Method
The authors leverage a framework that enhances the robustness of orthogonalization-based optimization by addressing two key limitations in existing methods: sensitivity to matrix dimensions and vulnerability to outlier-induced gradient noise. The overall approach integrates adaptive coefficient learning for the Newton-Schulz iteration and outlier suppression via soft-thresholding, forming a unified optimization process.
At the core of the method is the Newton-Schulz (NS) iteration, which approximates the orthogonal transformation (MtMtT)−1/2Mt by iteratively refining an initial matrix X0=Mt/∥Mt∥F. The update rule at each iteration k is defined as:
Xk=aXk−1+bXk−1(Xk−1TXk−1)+cXk−1(Xk−1TXk−1)2This recurrence operates on the singular values of the input matrix through a polynomial mapping g(x)=ax+bx3+cx5, and after T iterations, the resulting matrix XT approximates the orthogonalized momentum. The standard Muon optimizer employs fixed coefficients a=3.4445, b=−4.7750, and c=2.0315, which are optimized for average matrix shapes but exhibit poor performance on matrices with varying dimensions.
To overcome this dimensional fragility, the authors introduce an adaptive Newton-Schulz iteration (AdaNewton), where the coefficients a(m,n), b(m,n), and c(m,n) are learned specifically for each matrix size (m,n) in the network. This fine-grained adaptation ensures consistent orthogonalization quality across layers of different dimensions. The adaptive update rule is given by:
Xk=a(m,n)Xk−1+b(m,n)Xk−1(Xk−1TXk−1)+c(m,n)Xk−1(Xk−1TXk−1)2The coefficients are optimized jointly with the model parameters during training, allowing the orthogonalization process to adapt to the spectral properties of each layer. This approach shifts from a one-size-fits-all strategy to a dimension-robust design, ensuring stable and reliable gradient updates throughout the network.
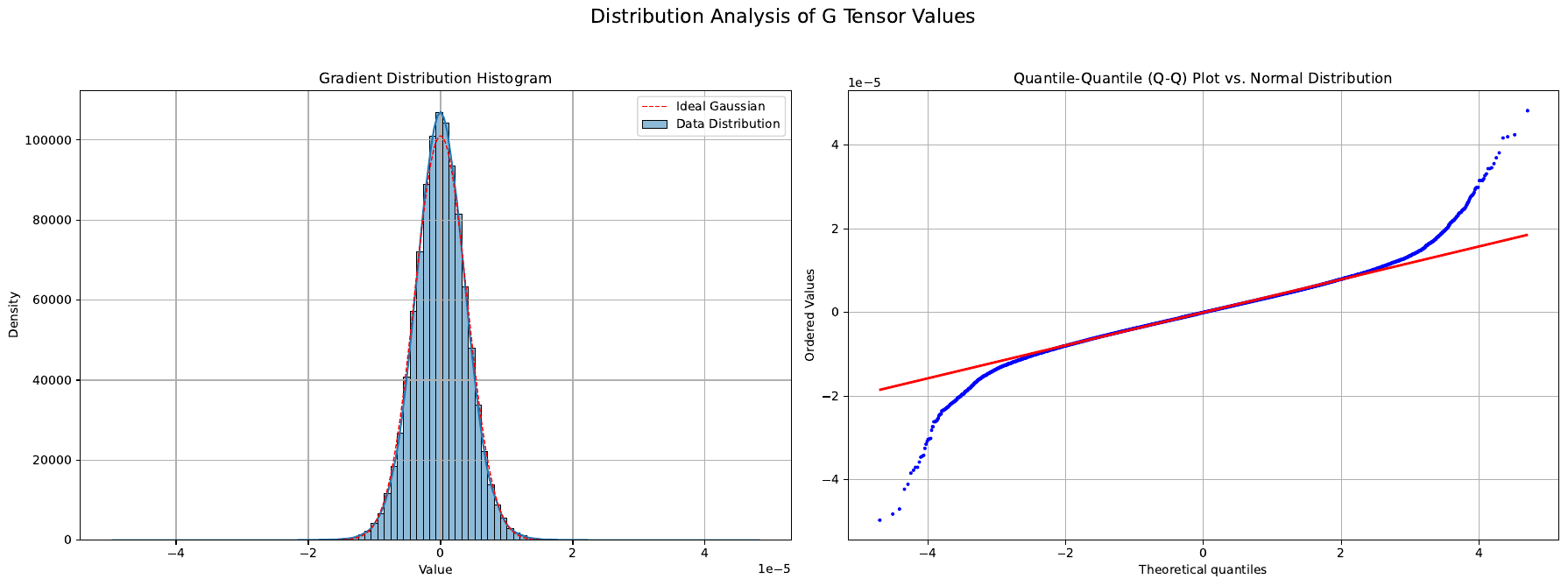
[[IMG:|Framework diagram of the ROOT optimizer]]
The framework diagram illustrates the integration of adaptive orthogonalization and outlier suppression. The momentum matrix Mt is first decomposed into a base component Bt and an outlier component Ot using soft-thresholding. The outlier component is discarded, while the base component undergoes robust orthogonalization via AdaNewton. The resulting orthogonalized matrix is then used to update the model parameters.
To further enhance robustness, the method incorporates soft-thresholding to suppress gradient outliers. The momentum matrix Mt is modeled as the sum of a base component Bt and an outlier component Ot, and the robust decomposition is formulated as a convex optimization problem that penalizes large-magnitude elements. The solution to this problem is given by the soft-thresholding operator:
Tε[x]i=sign(xi)⋅max(∣xi∣−ε,0)This operation smoothly shrinks gradient values beyond a threshold ε, preserving the relative ordering of magnitudes while dampening extreme values. The decomposition is applied element-wise to the momentum matrix, yielding:
Ot=Tε(Mt),Bt=Mt−OtBy applying orthogonalization only to the clipped base component Bt, the method ensures that the sensitive NS iteration operates on stable gradients, mitigating the amplification of outlier noise. This design provides a continuous, differentiable alternative to hard clipping, maintaining gradient direction while improving training stability. The complete optimization process is summarized in the ROOT optimizer algorithm, which combines momentum accumulation, outlier suppression, and adaptive orthogonalization in a single iterative loop.
Experiment
- Gradient Dynamics Validation: Compared orthogonalization strategies using gradients from the first 10k pre-training steps; ROOT maintained lower relative error than Muon and Classic Newton-Schulz, confirming that dimension-aware coefficients better approximate ground-truth SVD.
- LLM Pre-training: Trained a 1B Transformer on FineWeb-Edu subsets (10B and 100B tokens); ROOT achieved a final training loss of 2.5407, surpassing the Muon baseline by 0.01.
- Academic Benchmarks: Evaluated zero-shot performance on tasks like HellaSwag and PIQA; ROOT achieved an average score of 60.12, outperforming Muon (59.59) and AdamW (59.05).
- Ablation Studies: Identified a 0.90 percentile threshold as optimal for outlier suppression and selected a Mixed (1:3) calibration strategy to ensure stability while preventing overfitting.
- Vision Generalization: Trained a Vision Transformer on CIFAR-10; ROOT consistently achieved higher accuracy than the Muon baseline, validating the method's effectiveness on non-language modalities.
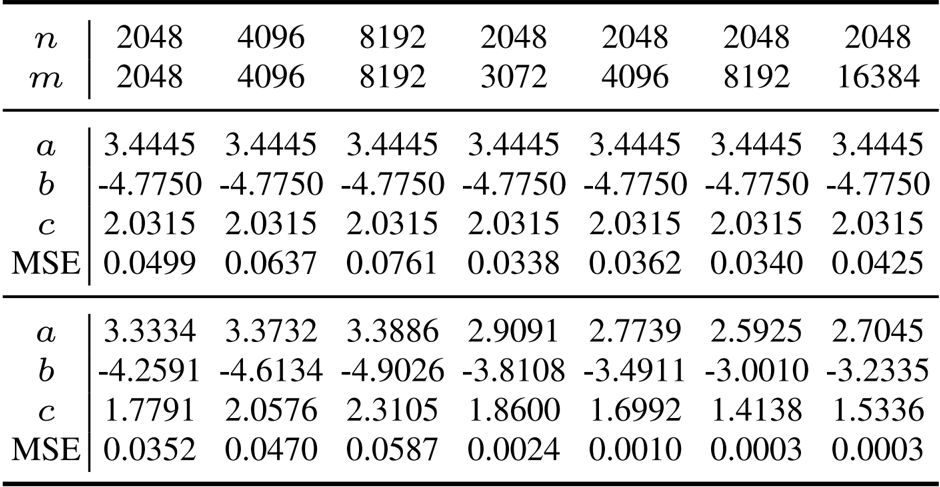
The authors use the provided table to demonstrate that the ROOT optimizer's shape-specific coefficients achieve lower mean squared error (MSE) across various matrix dimensions compared to fixed-coefficient methods. Results show that the MSE decreases significantly as the coefficient values adapt to different matrix shapes, indicating improved approximation fidelity for diverse layer geometries during training.
The authors evaluate the ROOT optimizer against AdamW and Muon on a range of academic benchmarks, showing that ROOT achieves higher zero-shot performance across all tasks. Specifically, ROOT outperforms both baselines in HellaSwag, PIQA, OBQA, SciQ, Wino, and WSC, with an average score of 60.12, surpassing AdamW's 59.05 and Muon's 59.59.

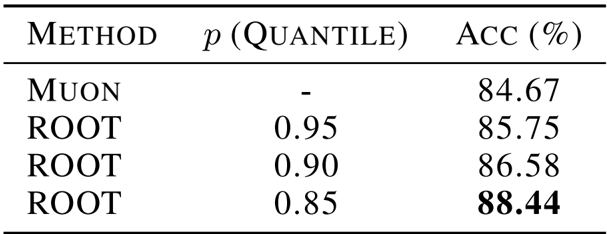
The authors evaluate the impact of different percentile thresholds for outlier suppression in the ROOT optimizer on a Vision Transformer trained on CIFAR-10. Results show that the choice of threshold significantly affects performance, with a lower percentile of 0.85 yielding the highest accuracy of 88.44%, outperforming both the Muon baseline and other ROOT configurations. This indicates that more aggressive outlier suppression can enhance generalization in vision tasks.
Build AI with AI
From idea to launch — accelerate your AI development with free AI co-coding, out-of-the-box environment and best price of GPUs.