Neural Network Basics: Backpropagation Algorithm

Geoffrey Hinton

Geoffrey Hinton is a British-born Canadian computer scientist and psychologist who has made many contributions to the field of neural networks. He is one of the inventors of the backpropagation algorithm and an active promoter of deep learning. He is known as the father of neural networks and deep learning.

In addition, Hinton is the founder of the Gatsby Centre for Computational Neuroscience at the University of London and is currently a professor in the Department of Computer Science at the University of Toronto in Canada. His main research direction is the application of artificial neural networks in machine learning, memory, perception and symbol processing. Currently, Hinton is exploring how to apply neural networks to unsupervised learning algorithms.

However, among Hinton's many scientific research results, back propagation is the most famous and is also the basis of most supervised learning neural network algorithms, which is based on the gradient descent method. Its main working principle is:

In actual operation, the ANN algorithm is generally divided into three categories: input layer, hidden layer and output layer. When there is an error between the algorithm output result and the target result, the algorithm will calculate the error value, and then feed the error value back to the hidden layer through back propagation, adjust it by modifying relevant parameters, and repeat this step until the expected result is obtained.

Backpropagation allows the ANN algorithm to derive results that are closer to the target. However, before understanding how backpropagation is applied to the ANN algorithm, it is necessary to first understand the working principle of ANN.

ANN is a mathematical model or computational model based on the human brain neural network, which is composed of a large number of nodes (which can be understood as biological neurons) connected to each other.

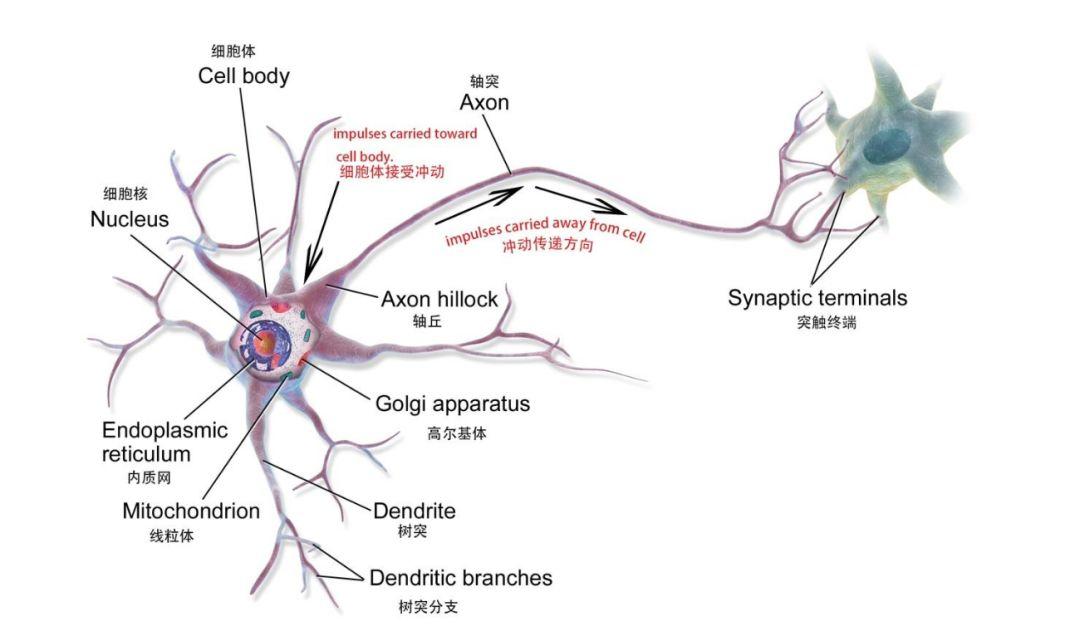
Biological Neurons

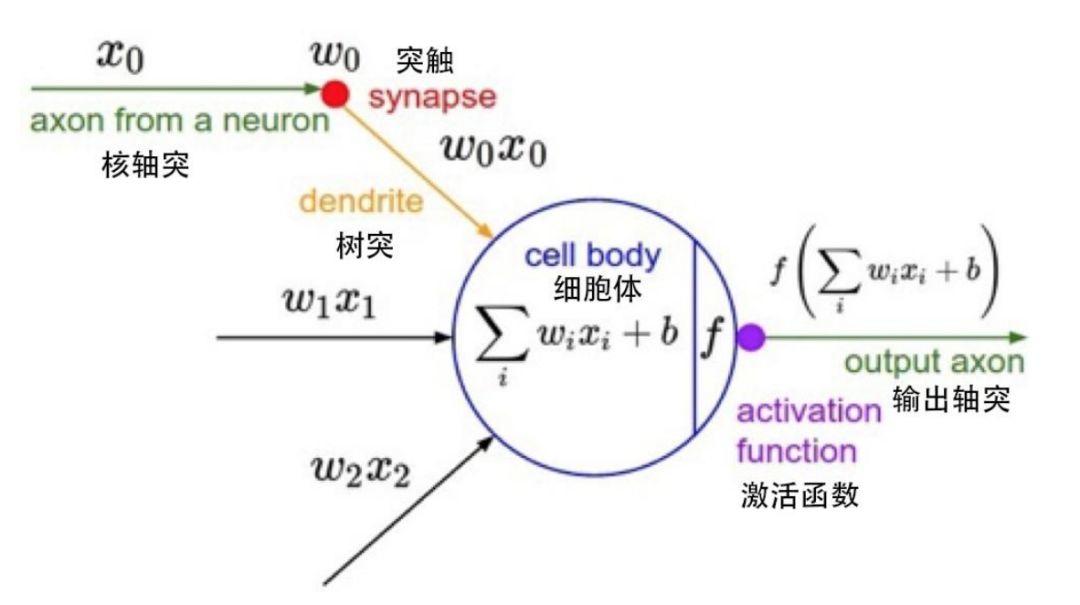
A single node in a mathematical model

Each node represents a specific output function, called an activation function; the connection between two nodes represents a weighted value, also called a weight value. During the operation of the ANN algorithm, each connection corresponds to a weight w and an offset b (also called an ANN parameter). The output value is related to the node, weight value, and offset.

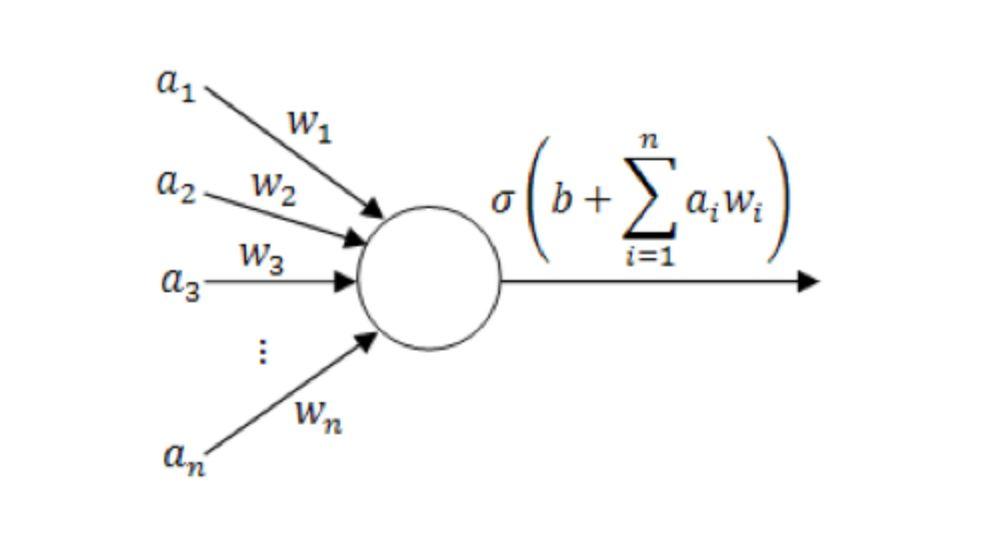
Single neuron model diagram

(where a1~an are the components of the input vector; w1~wn is the weight value; b is the offset; σ is the activation function, such as tanh, Sigmoid, ReLU, etc.)

A complete ANN generally consists of an input layer, multiple hidden layers and an output layer. The hidden layer is mainly composed of neurons, which undertake the most important computing work. In the actual operation process, the neurons in each layer will make decisions and transmit the decisions to the neurons in the next hidden layer until the final result is output.

Therefore, the more hidden layers there are, the more complex the ANN is and the more accurate the results are. For example, if you want to use an ANN to determine whether an input animal is a cat or not a cat, the neurons in each hidden layer will make a judgment on it, get a result, and transmit the result downward until the last layer of neurons outputs the result.

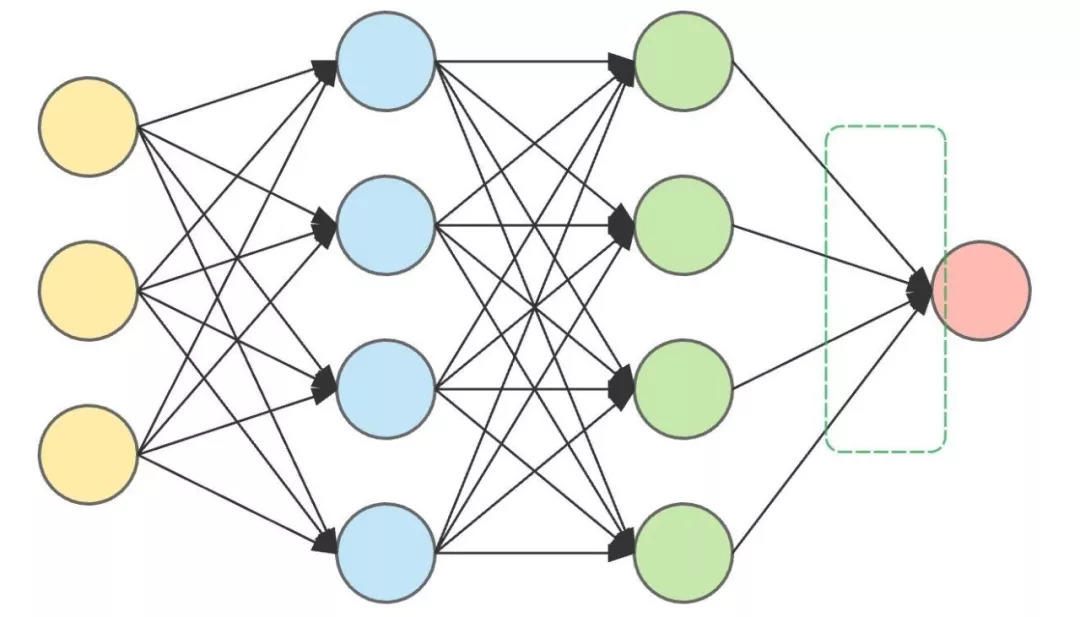
This is an ANN architecture with two hidden layers.

The input layer (left) and output layer (right) are on both sides, and the two hidden layers are in the middle.

If the animal is biologically a cat, but the ANN says it is not a cat, then the ANN output is wrong. Now, the only thing to do is to go back to the hidden layer and adjust the weights and biases. This process of going back and adjusting the data is backpropagation.

However, to achieve back propagation, we also need to rely on an important type of algorithm - gradient descent algorithm. Gradient descent greatly speeds up the learning process. It can be simply understood as: when going down the mountain from the top of the mountain, choosing a path with the steepest gradient is the fastest.

Because we need to constantly calculate the deviation between the output and the actual value to modify the parameters (the greater the difference, the greater the modification), we need to use an error function (also called a loss function) to measure the error between the final predicted value and the actual value of all samples in the training set.

in y^i is the prediction result, yi For actual results.

This expression measures the error between the final predicted value and the actual value of all samples in the training set, which is only related to the predicted category of the output layer, but this predicted value depends on the parameters in the previous layers. If we don’t want to think that dogs are cats, we need to minimize this error function.

Gradient descent is one of the algorithms that minimizes the error function. It is also a commonly used optimization algorithm in ANN model training. Most deep learning models use gradient descent for optimization training. Given a set of function parameters, gradient descent starts from a set of initial parameter values and iteratively moves to a set of parameter values that minimize the loss function. This iterative minimization is implemented using calculus, taking gradual changes in the negative direction of the gradient. A typical example of using gradient descent is linear regression. As the model iterates, the loss function gradually converges to the minimum value.

Since the gradient expresses the direction of the maximum rate of change of a function at a certain point and is obtained by calculating the partial derivative, using the gradient descent method will greatly speed up the learning process.

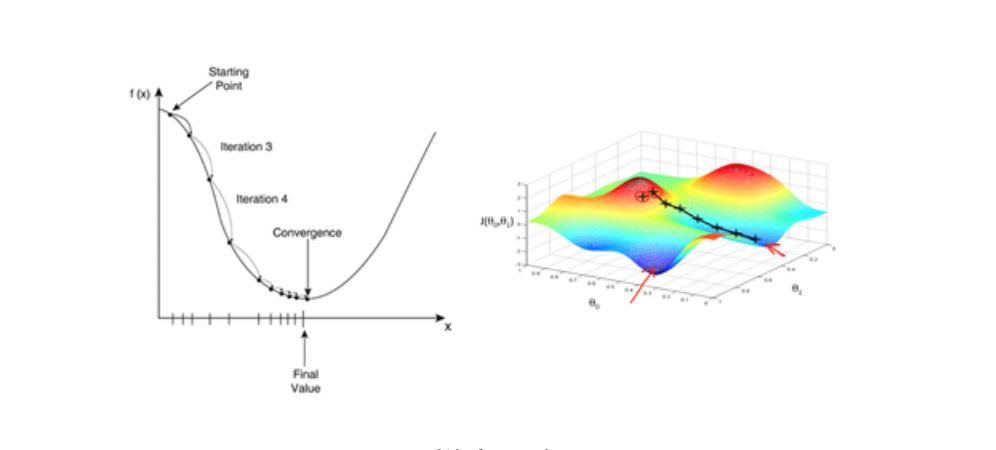
Gradient Descent

In practice, it is theoretically necessary to first check how the weights and offsets in the last layer affect the result. By taking the partial derivative of the error function E, we can see the influence of the weights and offsets on the error function.

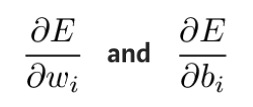
These partial derivatives can be calculated using the chain rule to find out the effect of these parameter changes on the output. The derivative formula is as follows:

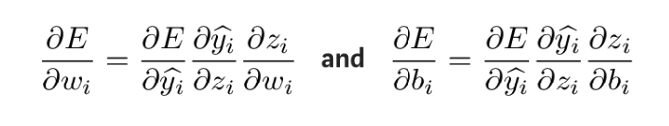
To obtain the unknown quantity in the above expression, take the partial derivative of zi with respect to wi and bi respectively:

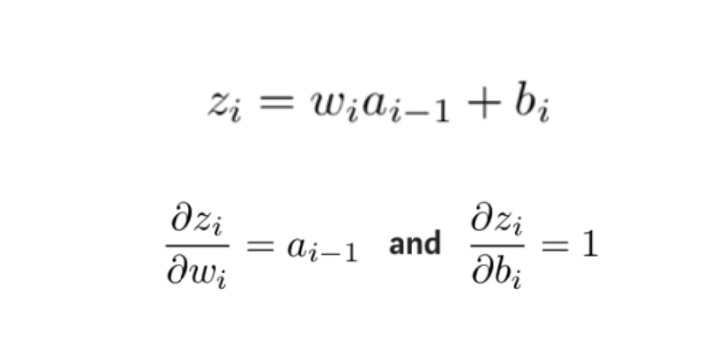Then, the partial derivatives of the error function with respect to the weights and offsets of each layer are calculated in reverse order, and the adjusted weights and offsets are updated by the gradient descent method until the initial layer where the error occurs.

This process is the back propagation algorithm, also known as the BP algorithm, which propagates the error of the output layer backwards layer by layer, and updates the network parameters by calculating partial derivatives to minimize the error function, so that the ANN algorithm can obtain the expected output.

Currently, backpropagation is mainly used in ANN algorithms under supervised learning.