Command Palette
Search for a command to run...
The Paper of the Institute of Semiconductors of the Chinese Academy of Sciences Was Published in the Top Journal of TNNLS Again, Contributing a New Perspective on Exploring Mathematical Expressions
Solving mathematical expressions is a very important research topic in the field of machine learning, and symbolic regression (SR) is a method to find precise mathematical expressions from data.
Symbolic regression is used to reveal the underlying mathematical expression of given observational data. It has a natural ability to explain and generalize, and can explain the causal mechanisms between variables or predict the development trends of complex systems. It is also widely used in different fields such as physics and astronomy.
A famous application case is Kepler's discovery of the orbits of planets. Scientists have discovered some new laws of celestial motion through symbolic regression algorithms, and thus deduced their orbits. This has made an important contribution to human exploration of the vast universe.
However, symbolic regression research also has its own difficulties. Symbolic regression focuses on obtaining the best combination of these elements and solving the most appropriate coefficients given the independent variable X and the dependent variable Y. However, obtaining the best combination is an NP-hard problem (non-deterministic polynomial), and the combination space grows exponentially with the length of the symbolic expression. In addition, the nonlinear solution process of the coefficients and the element combination optimization process interfere with each other, so it is very time-consuming to determine the exact expression.
In response to this academic problem,Researchers from the Institute of Semiconductors, Chinese Academy of Sciences, regarded the solution of expression structure as a classification problem and solved it through supervised learning, proposing a symbolic network called DeepSymNet to represent symbolic expressions.Compared with several popular SR algorithms based on supervised learning, DeepSymNet uses shorter labels, reduces the prediction search space, and improves the robustness of the algorithm.

Paper address:
https://ieeexplore.ieee.org/document/10327762
Follow the official account and reply "DeepSymNet" to download the paper
Limitations of existing methods highlighted
There are two main types of solutions to the currently popular symbolic expression structure:
- Search-based solutions
The classic search-based scheme is the GP (genetic programming) algorithm. First, many expressions are randomly obtained as the initial population, and then evolved through replication, exchange and mutation, and the offspring with smaller goodness are selected to continue evolving until the expression meets the goodness requirement.
In addition, among the search-based methods, an important class of methods uses reinforcement learning to search for suitable expression structures, such as the DSR algorithm, which encodes the symbol tree as a sequence and uses the policy gradient method in deep reinforcement learning to solve it. The idea behind DSR is to increase the sampling probability of expressions with larger rewards, thereby producing expressions with smaller errors.
There is also an SR algorithm for physical formulas - AIFeynman, which mainly uses prior knowledge in physics to judge the expression structure, thereby decomposing the expression into smaller sub-problems and narrowing the search space; another method based on sparse optimization - EQL, mainly uses the BP algorithm combined with sparse optimization to learn parameters, thereby obtaining a sparse sub-network in the EQL network, and then obtaining the mathematical expression structure.
In addition to their own obvious shortcomings, this type of method has the common disadvantage of being slow because the search space is large and the solution experience cannot be reused.
- Supervised learning-based solutions
Supervised learning-based solutions can overcome the time-consuming shortcomings of search-based solutions. Representative methods include SymbolicGPT, NeSymReS and E2E.
* SymbolicGPT encodes symbolic expressions into strings and regards the expression structure solution as a language translation task. The GPT model in the language translation process uses a large number of artificially generated samples for supervised training;
* NeSymReS encodes the symbol tree as a sequence via pre-order traversal and trains it using set Transformer;
* E2E encodes expression structure and coefficients into labels for training, thereby predicting expression structure and coefficients simultaneously.
However, these solutions have problems of multiple equivalent labels and unbalanced training samples, which can easily cause ambiguity during the training process and affect the robustness of the algorithm.In addition, they have other shortcomings. For example, SymbolicGPT considers relatively simple expressions because the number of symbols used for sampling is at most four layers; E2E encodes coefficients as labels, which makes the labels very long and affects the prediction accuracy, etc.
A new approach to solving problems - DeepSymNet
Researchers from the Institute of Semiconductors, Chinese Academy of Sciences, proposed a new symbolic network called DeepSymNet to represent symbolic expressions and presented the overall framework of DeepSymNet.The first layer is the data, the middle layer is the hidden layer, and the last layer is the output layer.

The hidden layer nodes are composed of operation symbols, including +, -, ×, ÷, sin, cos, exp, log, id, etc., where the id operator is the same as the id operator in EQL.
The number of id operators in each hidden layer is equal to the number of nodes in the previous layer, while other operators appear only once in each hidden layer. The operator id corresponds one-to-one with the nodes in the previous layer, which enables each layer to utilize all the information of the previous layer. Other operators are ordinary operators and are fully connected to the previous layer.
The connection between the id operator and the previous layer is fixed, and the ordinary operator has no connection to the previous layer, or one or two connections, which means that in this network a subnetwork represents a symbolic expression. The more hidden layers an expression occupies, the higher the complexity of the expression. Therefore, the number of hidden layers can be used to roughly measure the complexity of the expression.
But please note that the input layer has a special node "const" to represent constant coefficients in symbolic expressions. Only the edges connected to the "const" node have weights (constant coefficients) to prevent enough constant coefficients from appearing in the symbolic expression.
all in all,DeepSymNet is a complete network that can represent any expression. Solving SR is the process of searching for subnetworks in DeepSymNet.
Two groups of experimental comparisons show the advantages
The research team conducted tests based on artificially generated datasets and public datasets, and compared currently popular algorithms.
Dataset download address:
https://hyper.ai/datasets/29321
In the experiment, DeepSymNet has up to 6 hidden layers and supports up to 3 variables. The research team generated 20 samples for each label, each containing 20 data points. The sampling interval of constant coefficients and variables is [-2,2]. The training strategy is early stopping (that is, training is stopped when the loss on the validation set no longer decreases). It is assisted by the Adam optimizer.
- Test results on artificially generated data
The test results show:
* The difficulty of prediction increases as the number of prediction objects increases, and the hidden layer (i.e. complexity) of the expression also increases;
* The bottleneck of label prediction lies in the choice of operator;
* DSN2 solves the optimal and approximate solutions better than DSN1;
* Equivalent label merging and sample balancing can enhance the robustness of the algorithm.
first,DeepSymNet can represent expressions more efficiently than symbolic trees, and for the same module that appears multiple times in an expression, the average label length of DeepSymNet is shorter than that of NeSymRes.

The prediction accuracy of the model trained with DeepSymNet labels is much higher than that of the model trained with NeSymReS labels, as shown in the figure above. This shows that DeepSymNet labels are superior to symbolic tree labels.
Secondly,As the number of hidden layers occupied by expressions increases, the prediction accuracy of the model decreases rapidly. Therefore, the research team proposed that label prediction can be divided into two subtasks: operator prediction and connection relationship prediction, to ensure that the label prediction problem can be better solved.

The results of training DeepSymNet in two parts show that as the number of hidden layers increases, the prediction accuracy of operator selection drops sharply, while the prediction accuracy of connection relationship remains high. This is because the operator selection space is much larger than the connection relationship selection space. Therefore, in order to improve the accuracy of operator selection, the researchers trained the operator selection separately.

In the prediction process, the team first used the operator selection model to obtain the operator selection sequence, and then input it into the trained model DSN1 to predict the connection relationship. The test results are shown in the figure above. After training the operator selection separately, the prediction accuracy is greatly improved. The separately trained model is called DSN2.
In addition, the researchers also conducted ablation experiments to verify the robustness of equivalent label merging and sample balance enhancement. First, 500,000 training samples were randomly selected, which contained 128,455 different labels (TrainDataOrg). The results showed that the sample number distribution of these labels was seriously uneven, with the minimum sample number being 1, the maximum sample number being 13,196, and the sample number variance being 13,012.29.

The team then balanced the number of samples to obtain training samples TrainDataB and training samples TrainDataBM after merging equivalent labels.
Then, based on the three training data, the models DSNOrg, DSNB and DSNBM were obtained. These three models were tested on the test set. The accuracy of the three models increased from the beginning to the end.This shows that after increasing sample balance and merging equivalent labels, the accuracy of the model in finding the optimal solution has been improved, which has indeed enhanced the robustness of the algorithm and improved the performance of the algorithm.
- Public dataset test results
The research team used 6 test datasets:Koza , Korns, Keijzer, Vlad, ODE and AIFeynman, and expressions with no more than 3 variables were selected from these data sets for testing. Comparison with the currently popular supervised learning-based methods shows that the accuracy of the proposed algorithm (DSN1, DSN2) is better than the comparison algorithm.
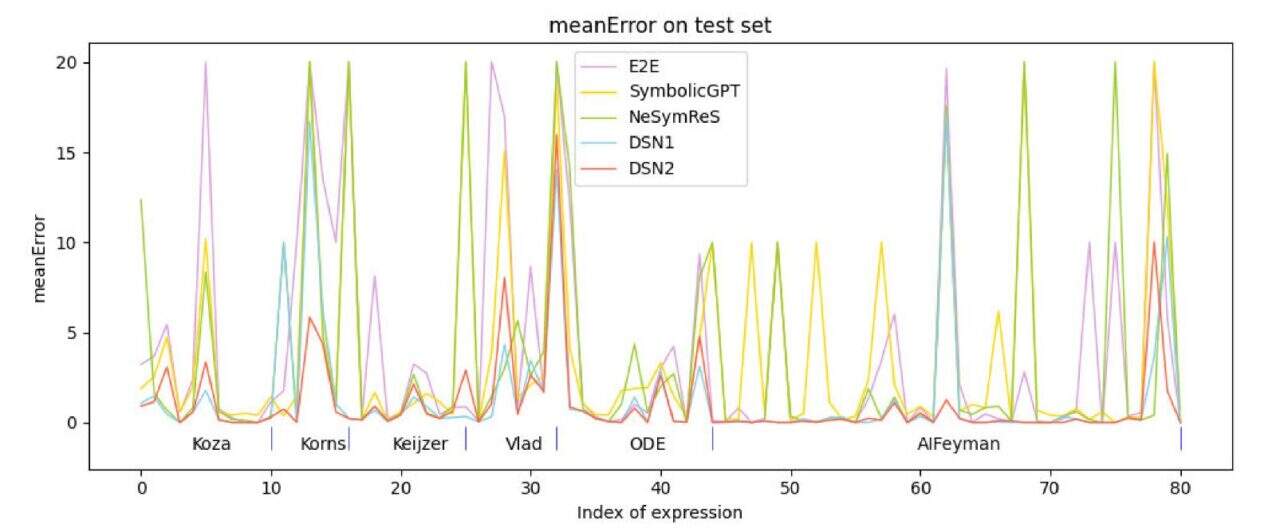
In addition, the team compared the algorithm with the currently popular search-based methods EQL, GP, and DSR, and the results are shown in the figure below.
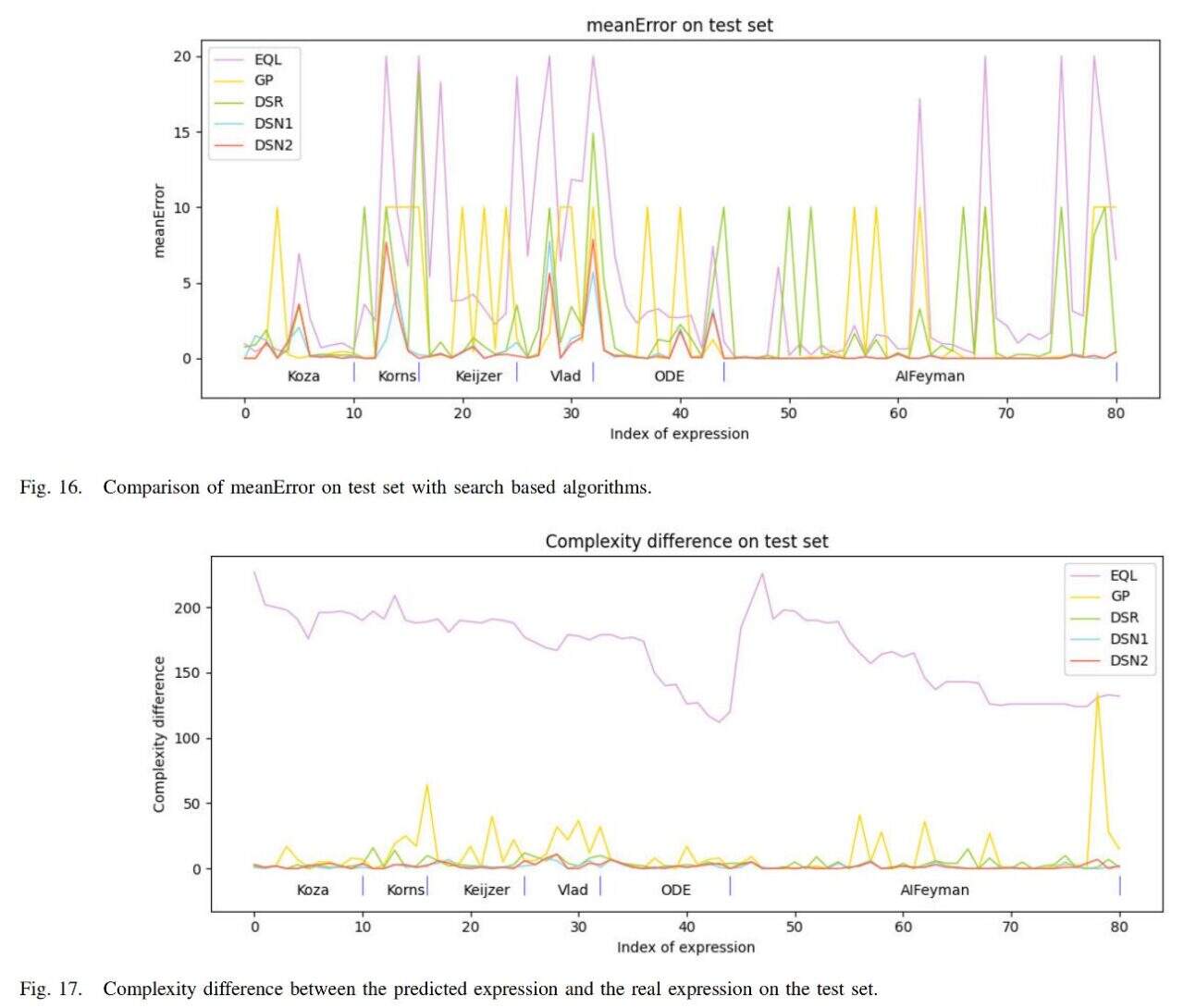
The average error of the algorithm (DSN1, DSN2) is the smallest, and the complexity of the expression obtained is also closest to the complexity of the true expression.
In summary, based on the results, it can be concluded thatThe algorithm studied by the team outperforms the comparative algorithms in three aspects: symbolic expression error, symbolic expression complexity and running speed, which confirms the effectiveness of the algorithm.
The team behind the scenes is star-studded
Scientists around the world are working hard on the core problem of symbolic regression. Although the paper mentions that DeepSymNet still has some limitations, this research still makes an important contribution to artificial intelligence in solving mathematical problems. By treating it as a classification problem, it undoubtedly provides a new solution for supervised learning-based SR methods.
Of course, this achievement is inseparable from the passion and sweat of a group of people, such as Wu Min, the first author of the paper. According to the official website of the Institute of Semiconductors of the Chinese Academy of Sciences,Wu Min is currently an assistant researcher at the Institute of Semiconductors, Chinese Academy of Sciences. He has participated in several scientific research projects, including "Symbolic regression based on deep learning and its application in semiconductor device research and development" and "Knowledge fusion neural network divide-and-conquer simplification symbolic regression method".
in addition,Dr. Jingyi Liu, one of the authors of the paper, was the first author of a paper published in the top artificial intelligence journal Neural Networks in July last year. The paper was titled "SNR: Symbolic Network-based Rectifiable Learning Framework for Symbolic Regression".A learning framework with correction capabilities is provided for the symbolic regression problem.
Judging from the research on related topics, the country is firmly leading the innovative methods. What can be expected in the future is that these theories and research results will surely make important contributions to solving practical problems in the near future.