AlphaGeometry: DeepMind's Massive Computing Power Creates Miracles Again, but "computing Power Instead of Intelligence" May Not Be the Optimal Solution

Author: Li Baozhu

Editor: Sanyang

Cover image source: Google DeepMind

DeepMind uses computing power to create miracles? How much gold is in the highly praised AlphaGeometry?

Recently, Google DeepMind's Alpha series has added a new member - AlphaGeometry, which is still very popular, with praises such as "milestone", "epic", and "close to humans" overflowing the screen. So, how much gold is this AI system that claims to have gold medal-level mathematical ability?

AlphaGeometry was developed by Google DeepMind team and researchers from New York University.Combining a neural language model with a symbolic deduction engine,Able to solve complex geometry problems at a level close to that of humans.

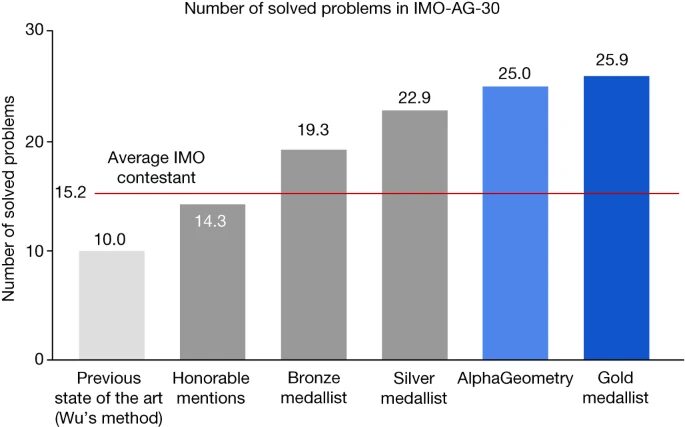
In a benchmark test of 30 International Mathematical Olympiad (IMO) geometry problems, AlphaGeometry solved 25 of them in the given time, which was previously SOTA  Wu's "Wu method" solved 10 problems, while the human IMO gold medalist could solve an average of 25.9 problems.

Indeed, since the launch of AlphaGo, along with many innovative breakthroughs in different disciplines, the positioning of "DeepMind products must be high-quality" has gradually taken root in people's minds. But at the same time, there are also rational and dialectical voices in the industry - computing power replacing intelligence is certainly gratifying, but the actual application value is more important. So, with the release of AlphaGeometry, we would like to talk about whether this is a carnival under the computing power advantage, or AI for Science  Pathfinder.

It is worth mentioning thatWe interviewed Professor of the School of Intelligence at Peking UniversityLin Zhouchen, and discussed and studied relevant academic issues.Professor Lin Zhouchen studied mathematics and applied mathematics at Nankai University, Peking University, and Hong Kong Polytechnic University, and then returned to the School of Mathematics at Peking University to pursue a doctorate degree and began to enter the field of artificial intelligence. (Click here to view the interview with Professor Lin Zhouchen)

Expression and computation: two major challenges of AI for Math

Professor Lin Zhouchen said:"In the past, the "expression" of mathematical theorems and the large-scale amount of computation were the two major challenges for AI to prove mathematical theorems."

“First of all, as a very abstract subject that relies heavily on logical reasoning, the first step for mathematics to embrace AI is to solve the “expression” problem. Expressing mathematical theorems in a way that computers can calculate is the basis for subsequent AI applications.”

The geometric problems that AlphaGeometry targets are relatively easy to express. The emergence of analytic geometry and algebraic geometry has made it possible to express geometric shapes and the relationship between geometric objects through numerical values.Wu WenjunThe "Mathematical mechanization"It also, to a certain extent, builds a bridge between plane geometry theorems and machine language."

"Secondly, the 'Wu method' proposed by Academician Wu Wenjun and traditional methods such as the Gröbner basis have theoretically solved the problem of proving theorems in plane geometry, but they are limited by computing power. In other words, due to the large amount of storage and computing, especially when facing more difficult plane geometry problems, the operation space will grow exponentially, so many previous methods have difficulty in handling difficult problems."

"The problem of large computational workload is obviously not the main obstacle for DeepMind, which has deep pockets. The main difficulty lies in how to avoid the exponential growth of the operating space, and machine learning methods can help at this time."

Specifically, AlphaGeometry is trained on 100 million synthetic data points, and can autonomously solve complex geometry challenges without human demonstrations and generate human-readable proofs.

As shown in the figure below, taking the "Isosceles Theorem" which is most familiar to primary and secondary school students in my country as an example, if you want to prove that ∠ABC=∠BCA, you need to manually convert the problem into computer language first, and then input it into AlphaGeometry.

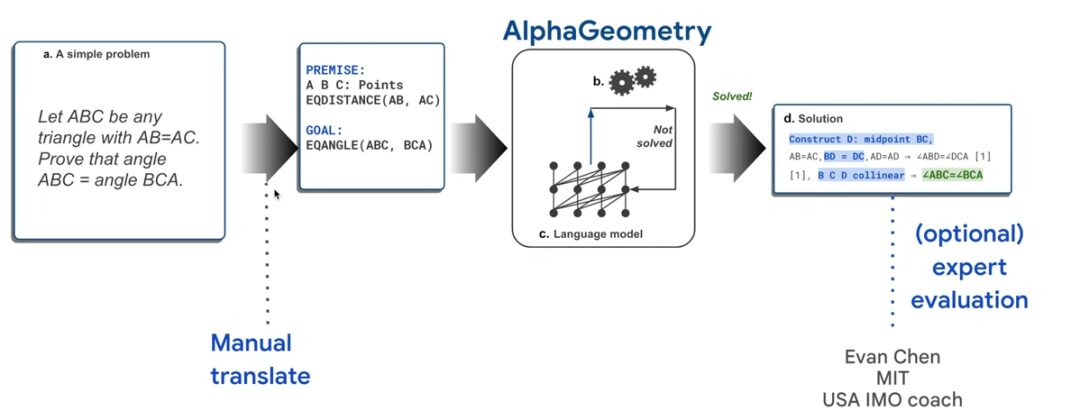
AlphaGeometry starts the proof search by running a symbolic deduction engine, which "exhaustively" deduces new statements from the theorem premises until the theorem is proved or the new statements are exhausted. If the symbolic deduction engine fails to find a proof, the language model builds an auxiliary point, adds provable conditions, and restarts the search for a proof through the symbolic engine. This cycle continues until a solution is found.

Solutions will be automatically parsed into human-readable language, so they can be verified and evaluated.

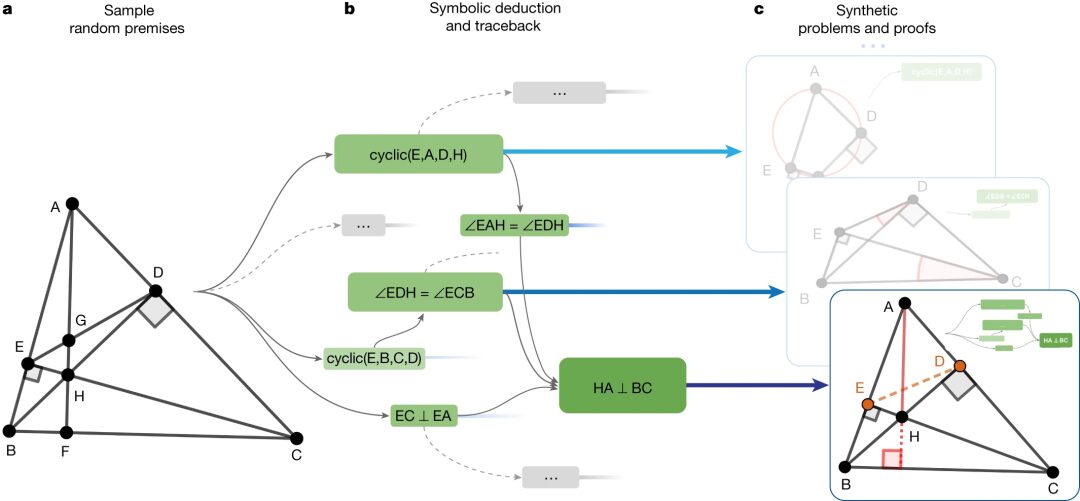
It is worth mentioning that AlphaGeometry uses synthetic data for model training, solving the problem of lack of relevant databases.

By using the existing symbolic engine on various random theorem premises and running it on 100,000 CPUs for 72 hours, the researchers obtained approximately 500 million synthetic theorem proof examples. After formal normalization and deduplication, they ultimately obtained 100 million theorem proof examples, of which 9 million examples involved at least one auxiliary construction, and many proof steps exceeded 200, which is four times the average proof length of geometry problems in the International Mathematical Olympiad.

In order to compare and test AlphaGeometry's ability to solve practical problems, the researchers tried to convert geometry problems in the IMO competition since 2000 into machine language readable by symbolic engines, and found that only 75% could be successfully expressed, thus forming a test set IMO-AG-30 consisting of 30 classic geometry problems.

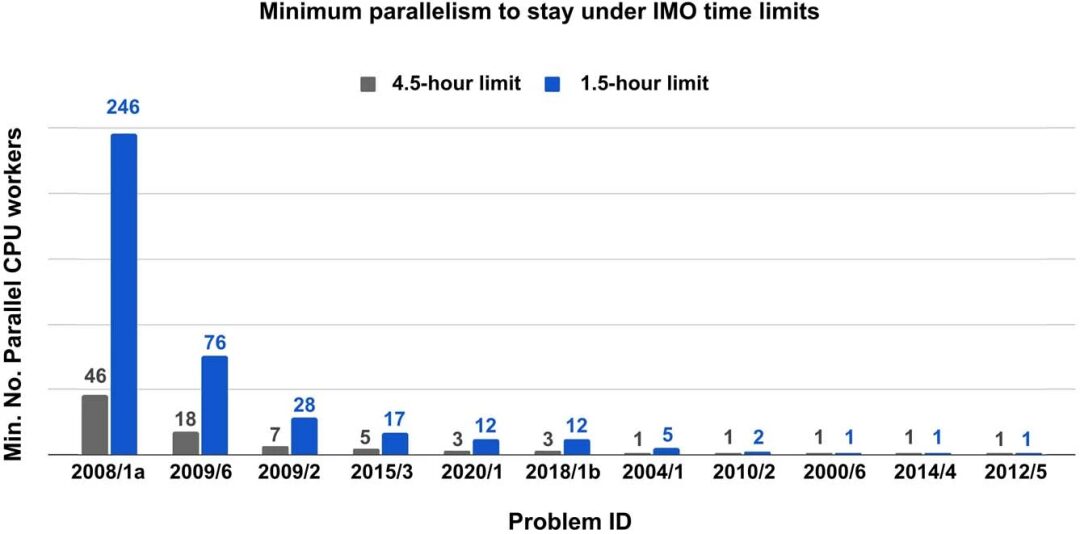
Each problem has a different running time because its derivation closure size varies. The researchers found that the running time does not correlate with the difficulty of the problem. For example, IMO 2019 P6 is much harder than IMO 2008 P1a, but requires much less parallelization time to solve within the IMO time limit.

Since the language model decoding process returns k different sequences, describing k optional auxiliary structures, the researchers performed beam search on the k options, using the score of each beam as its value function. This method has strong parallelism and can greatly improve the search speed when parallel computing resources are available.

The researchers found that the minimum number of parallel CPUs required to solve all 25 problems and stay within the time limit with four parallel copies of the GPU V100 accelerated language model is shown in the following figure:

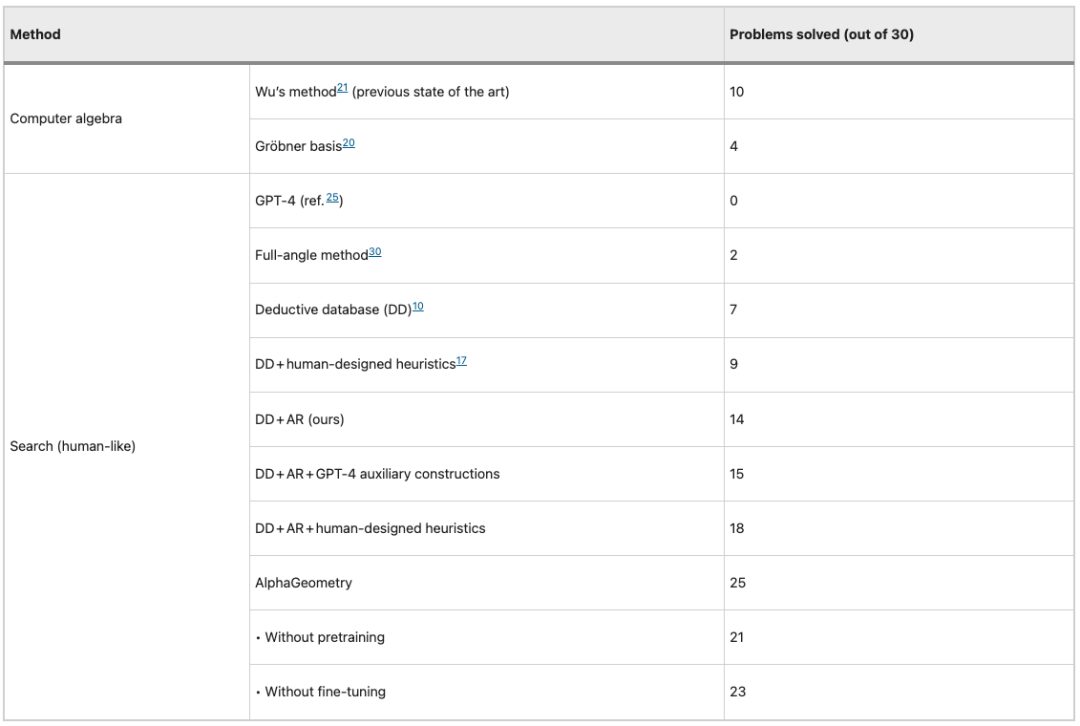
The performance of 10 different models/methods on the IMO-AG-30 test set is shown in the figure below. Interestingly, GPT-4 did not get any questions right in the test.

Behind the substitution of computing power for intelligence, application value is the key

In the past two days, the overwhelming reports on the Internet have fully revealed the achievements of AlphaGeometry. Its influence needs no elaboration, so we would like to explore, after the noise, what practical value can AlphaGeometry bring to scientific research and the development of AI applications?

Professor Lin Zhouchen said:At present, AlphaGeometry can become a "teacher" like AlphaGo and play a greater auxiliary role in teaching.In addition, AlphaGeometry’s breakthrough in model performance is undeniable, and it further demonstrates that “great power brings about miracles” - strong computing power advantages create strong model performance, which to some extent further adds confidence to researchers and companies who “advocate” computing power. ”

However, as Professor Lin Zhouchen said,In the field of AI, although we have witnessed the effectiveness of "computing power replacing intelligence" countless times, the final 1% breakthrough towards becoming an industry expert is still difficult to achieve with AI.

Therefore, for now, whether it is AlphaGeometry or other AI tools such as the GPT model, they are still "both teachers and friends" in people's daily lives and scientific research. The flexible use of AI tools has become a general trend. How to apply the "miracle" created by computing power to practical problems is the value of human beings that is difficult to replace.

Drawing lessons from the past and applying them to the present, the rapid rise of AI tools has many similarities with the popularization of computers. For example, it has revolutionized the way we work, replacing traditional methods with great momentum, and gradually becoming a criterion for assessing workplace capabilities... But in contrast, the limitations of AI tools are also more prominent, that is, specificity.

Professor Lin Zhouchen believes:Current AI tools lack uniformity, even if we only focus on mathematics, there is a big difference between AI tools developed for number theory and geometry, not to mention interdisciplinary AI tools. AI tools have not yet become a basic foundation like today's computers, which can be easily accessed. The current computer languages include C language, Java, Python, etc., and it is entirely possible to solve problems in multiple disciplines such as mathematics, physics, and chemistry based on any one of these languages, which reflects its versatility, but AI tools are not the same, just looking at the Alpha series will give you a clue. "

Therefore, Professor Lin Zhouchen believes that: "In the future, when AI tools can be abstracted and reused, AI for Science will be able to "become popular."

This is also a phenomenon that HyperAI has observed while continuously tracking the development of AI for Science. Some research groups or research teams will recruit a member who specializes in AI in addition to members of the discipline to develop the AI tools needed for the research, while the Science part is still left to traditional scientific researchers.

There is no doubt that AI’s help and improvement to the scientific research process has become increasingly obvious and is becoming a new trend, but is this AI+Science team model a long-term solution?

Professor Lin Zhouchen believes: "In the future, on the one hand, the threshold for using AI tools needs to be lowered and a certain degree of uniformity needs to be achieved, so that scientists can also combine and use the components of AI tools for different problems, just like computer programming; on the other hand, scientists also need to gradually improve their ability to use AI tools in order to give full play to the power of AI."

The road ahead is long and arduous, but it will eventually be reached. AI for Science has been initiated by DeepMind and other large companies, and has been promoted by national policies. It has already started a long journey, and the thorns need to be cleared by scientific research and industry to truly create value for human development in its implementation.

Finally, I would like to thank Professor Zhouchen Lin of the School of Intelligence at Peking University for his help and support in writing this article. Professor Zhouchen Lin’s research group is currently recruiting doctoral students. Students who meet the requirements are welcome to send their resumes to: zlin@pku.edu.cn

My motto is the famous quote of physicist Ludwig Boltzmann: Nothing is more practical than a good theory. I am now looking for PhD students with strong mathematical ability (but this does not mean you have to come from a mathematics department) and a strong interest in theoretical analysis, so that I can enjoy with me how to elegantly use mathematics to solve practical problems. Feel free to send me your resume.

——Lin Zhouchen