Sigmoid-FunktionEs handelt sich um eine übliche S-förmige Funktion, auch bekannt als S-förmige Wachstumskurve. Aufgrund ihrer monoton zunehmenden und invers monoton zunehmenden Eigenschaften wird die Sigmoid-Funktion häufig als Schwellenwertfunktion eines neuronalen Netzwerks verwendet, um Variablen zwischen 0 und 1 abzubilden.

Grundlegende Eigenschaften der Sigmoidfunktion

Die Form und das Bild der Sigmoidfunktion lauten wie folgt:

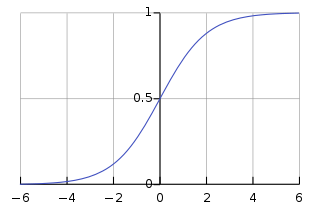
• Definitionsbereich: ( −∞ , +∞ )
• Bereich: (− 1, 1);
• Die Funktion ist innerhalb des Definitionsbereichs eine kontinuierliche, glatte Funktion;
• Es ist überall differenzierbar und seine Ableitung lautet: f′ ( x ) = f ( x ) ( 1 − f ( x ) );
• Die Funktion nimmt Werte zwischen 0 und 1 an, ist bei 0,5 zentral symmetrisch und weist eine größere Steigung auf, wenn sie sich x = 0 nähert.

Sigmoidfunktion und logistische Regression

Entsprechend dem Zweck der logistischen Regression LR müssen bei der Auswahl der Funktion die folgenden zwei Bedingungen erfüllt sein:

1) Der Wertebereich liegt zwischen 0 und 1;

2) Beim Auftreten eines Ereignisses ist 50% die Wasserscheide des Ergebnisses und die Auswahlfunktion sollte symmetrisch um 0,5 sein.

Basierend auf diesen beiden Punkten erfüllt Sigmoid genau die Anforderungen von LR.

Verwandte Begriffe: logistische Regression, Ventilfunktion