Nichtlineare Dynamische Reaktionsanalyse Des Koyna-Erdbebens Unter Berücksichtigung Des Hydrodynamischen Drucks
Einführung in das Tutorial
Einführung in Abaqus
Abaqus ist eine leistungsstarke Software zur Finite-Elemente-Analyse (FEA), die im Bereich der technischen Simulation weit verbreitet ist. Es simuliert und analysiert verschiedene technische Probleme mithilfe der Methode der finiten Elemente und kann Probleme von einfachen linearen Problemen bis hin zu komplexen nichtlinearen Problemen bewältigen. Abaqus wurde ursprünglich 1978 veröffentlicht und von Hibbitt, Karlsson & Sorensen, Inc. (HKS) entwickelt, das später in ABAQUS umbenannt und 2005 von Dassault Systèmes übernommen wurde.
Einführung in das Tutorial
Dieses Tutorial ist das offizielle Abaqus-Tutorial:Seismische Analyse einer Beton-Schwergewichtsstaumauer. Dieses Beispiel veranschaulicht eine typische Anwendung des Materialmodells für beschädigte Plastizität für Beton zur Bewertung der Stabilität und Beschädigung von Betonstrukturen, die beliebigen Belastungen ausgesetzt sind.
Das Tutorial analysiert den Koyna-Staudamm, der am 11. Dezember 1967 von einem Erdbeben der Stärke 6,5 auf der Richterskala erschüttert wurde. Dieses Problem wurde ausgewählt, weil es von vielen Forschern ausführlich analysiert wurde, darunter Chopra und Chakrabarti (1973), Bhattacharjee und Léger (1993), Ghrib und Tinawi (1995), Cervera et al. (1996) und Lee und Fenves (1998).
Einführung in die grundlegenden Parameter
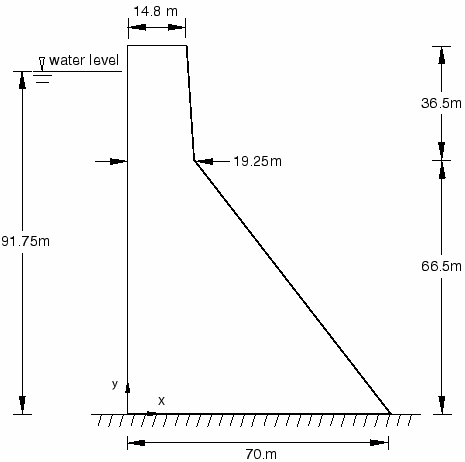
Die Querschnittsgeometrie eines typischen Abschnitts des Koyna-Staudamms ohne Überlauf ist in Abbildung 1 dargestellt. Dieser Dammabschnitt ist 103 Meter hoch und an der Basis 71 Meter breit. Es wird angenommen, dass die stromaufwärts gelegene Seite des Dammabschnitts vertikal ist. Die Wassertiefe des Reservoirs zum Zeitpunkt des Erdbebens beträgt hw=91,75 m. Den Forschern zufolge wurde eine zweidimensionale Analyse des Dammabschnitts ohne Überlauf unter ebenen Spannungsbedingungen in Betracht gezogen.
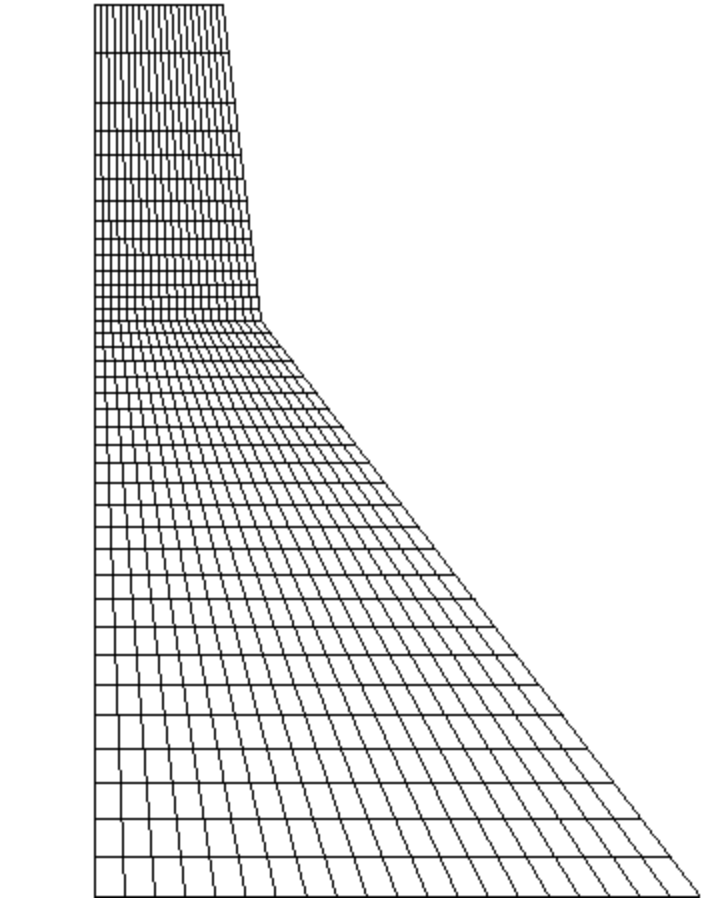
Das für die Analyse verwendete Finite-Elemente-Netz ist in Abbildung 2 dargestellt. Das Netz besteht aus 760 ebenen Spannungselementen erster Ordnung mit reduzierter Integration (CPS4R). Die Knoten werden in einem globalen rechteckigen Koordinatensystem definiert, dessen Mittelpunkt in der unteren linken Ecke des Damms liegt, wobei die vertikale Y-Achse nach oben und die horizontale X-Achse flussabwärts zeigt.
In diesem Beispiel ignorieren wir die Wechselwirkung zwischen dem Damm und dem Fundament, indem wir annehmen, dass das Fundament starr ist. Die dynamische Wechselwirkung zwischen dem Damm und dem Reservoir aufgrund der seitlichen Komponente der Bodenbewegung kann in einfacher Form mit der Westergaard-Methode der zusätzlichen Masse modelliert werden. Laut Westergaard (1933) entspricht der hydrodynamische Druck, den das Wasser während eines Erdbebens auf den Damm ausübt, einer bestimmten Wassermenge, die sich mit dem Damm hin und her bewegt, während der Rest des Reservoirs stationär bleibt. Die zusätzliche Masse pro Flächeneinheit der stromaufwärts gelegenen Oberfläche kann durch die Näherungsformel ausgedrückt werden:
, wobei y ≤ hw, ρw=1000kg/m3 ist die Dichte von Wasser. In der Abaqus/Standardanalyse wird die Methode der hinzugefügten Masse mithilfe einfacher 2-Knoten-Benutzerelemente implementiert, die in der Benutzer-Subroutine UEL codiert sind. Da der durch die vertikale Komponente der Bodenbewegung erzeugte hydrodynamische Druck als gering angesehen wird, wird er in allen Simulationen vernachlässigt.
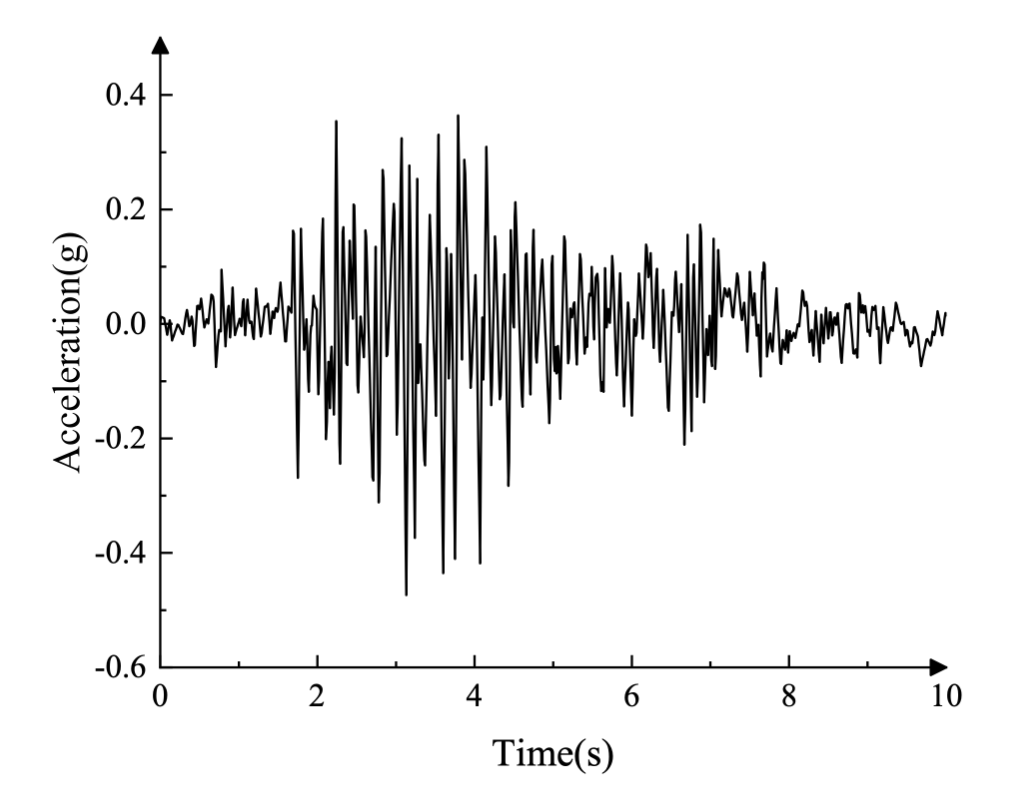
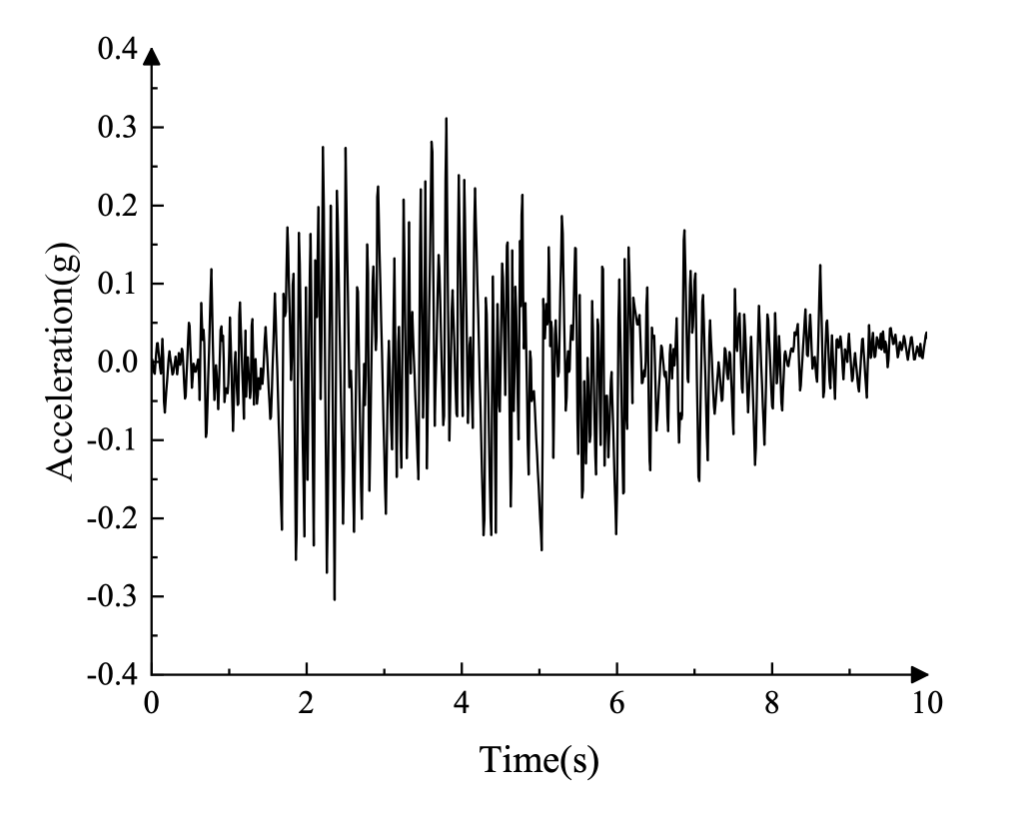
Die lateralen und vertikalen Komponenten der Bodenbeschleunigung, die während des Koyna-Erdbebens aufgezeichnet wurden, sind in Abbildung 3 dargestellt (in g = 9,81 m/s²). Vor der Erdbebenauslösung ist der Damm der Schwerkraftbelastung durch sein Eigengewicht und dem hydrostatischen Druck ausgesetzt, der durch das Reservoir auf der stromaufwärts gelegenen Seite erzeugt wird.
Das mechanische Verhalten von Betonmaterial wird durch das konstitutive Modell der Betonschädigungsplastizität simuliert. Die für die Simulation verwendeten Materialeigenschaften sind in Tabelle 1 und Abbildung 4 angegeben. Diese Eigenschaften gelten als repräsentativ für das Betonmaterial des Koyna-Staudamms und basieren auf den Eigenschaften, die von früheren Forschern verwendet wurden. Um diese Materialeigenschaften zu erhalten, wurden mehrere Annahmen getroffen. Besonders hervorzuheben ist die Kalibrierung des Zugverhaltens von Beton. Die Zugfestigkeit wird als die maximale Druckfestigkeit σ geschätzt.cu = 10% von 24,1 MPa und multipliziert mit einem dynamischen Vergrößerungsfaktor von 1,2, um Rateneffekte zu berücksichtigen; daher σt0 = 2,9 MPa. Um ungeeignete Ergebnisse aus der Netzempfindlichkeit aufgrund fehlender Bewehrung in der Struktur zu vermeiden, wird das Verhalten nach einem Zugversagen durch die Angabe einer Spannungs-/Verschiebungskurve anstelle einer Spannungs-Dehnungskurve angegeben, wie in Abbildung 4.1 dargestellt. Dies wird durch die Spannungs-/Verschiebungskurve nach dem Riss erreicht.
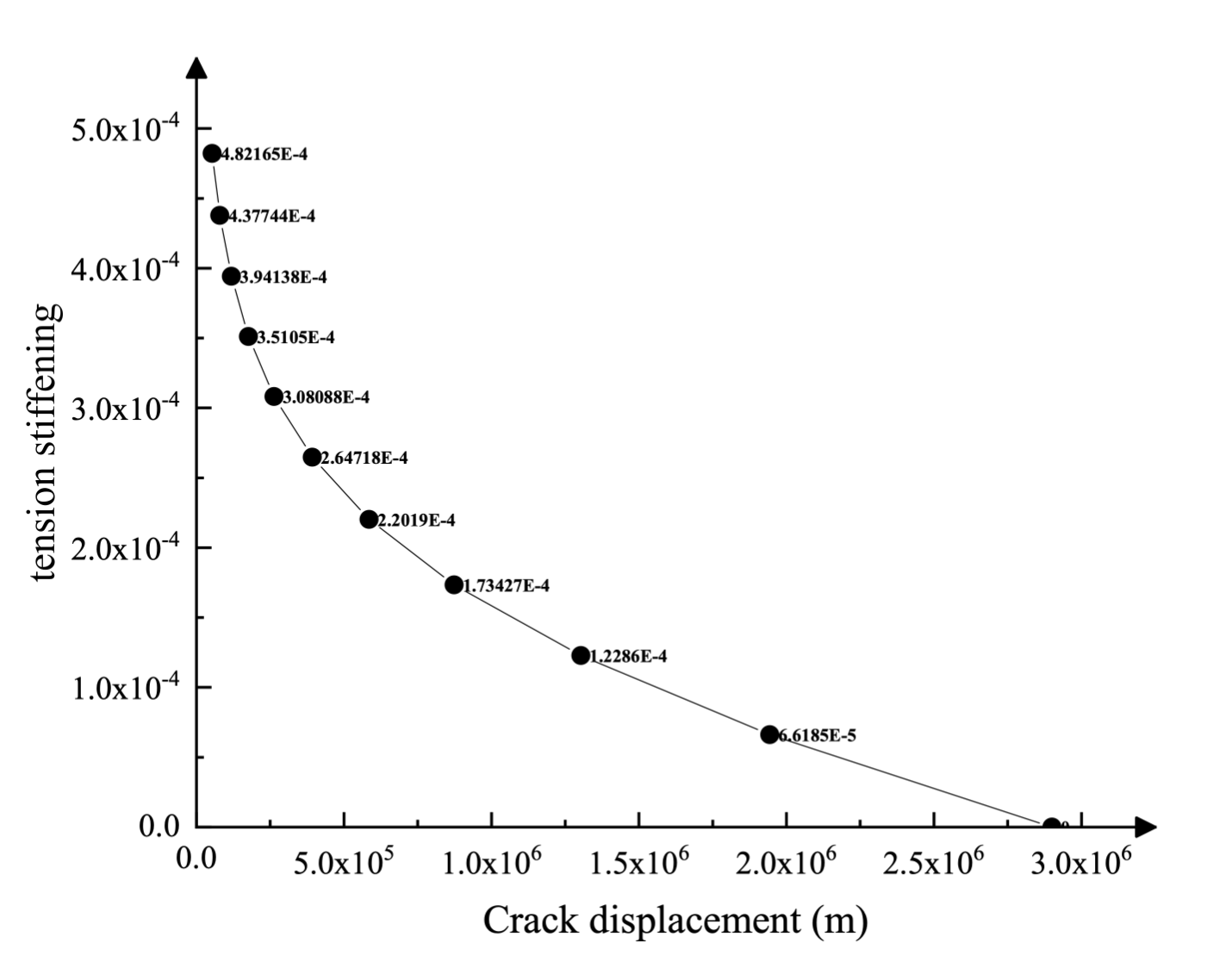
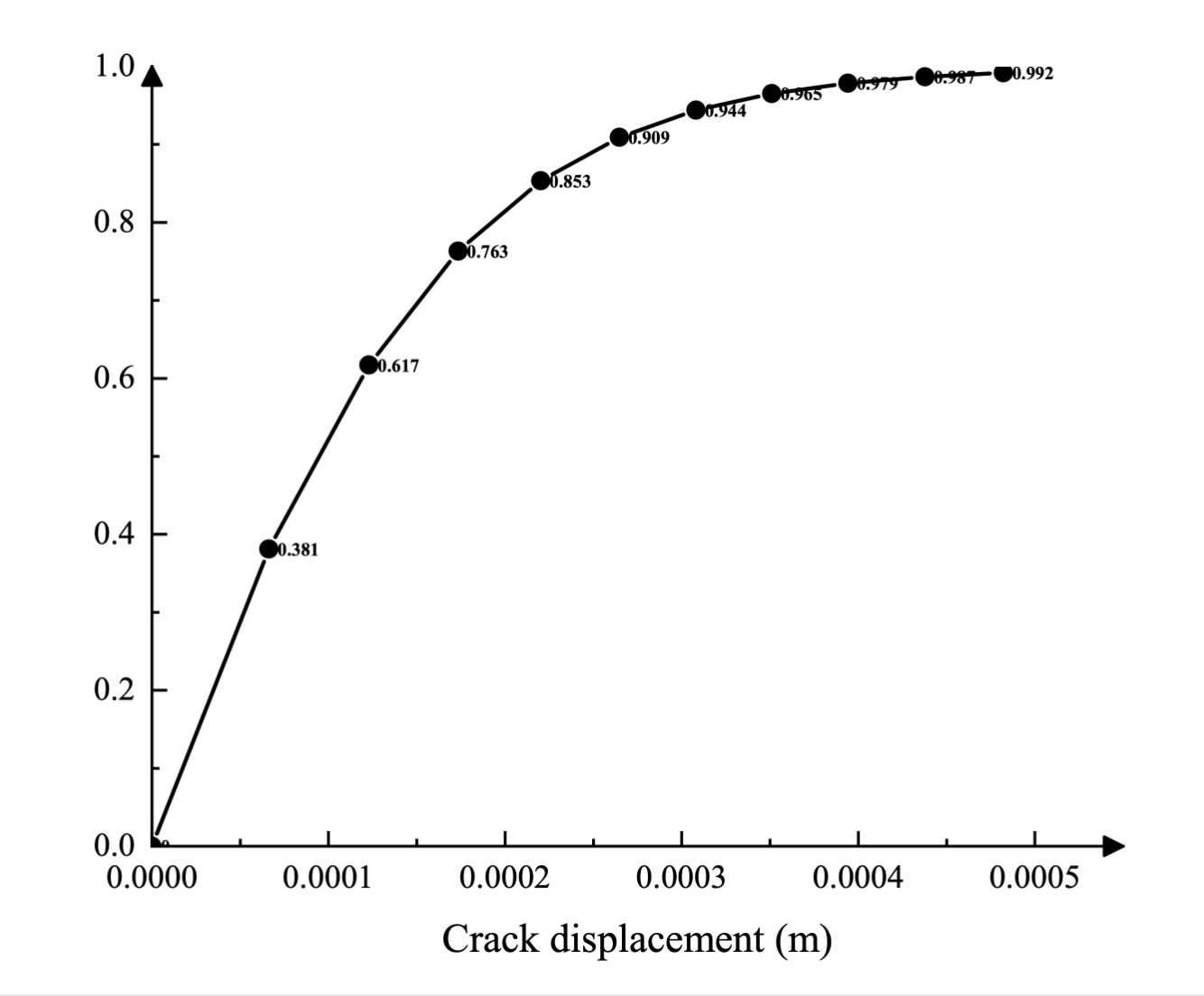
Ebenso wird der Zugschaden in tabellarischer Form als Funktion der Rissverschiebung unter Verwendung einer Post-Crack-Schadensverschiebungskurve angegeben. Die Kurve ist in Abbildung 4.2 dargestellt. Der durch Druckversagen (Zerdrücken) des Betons bedingte Steifigkeitsverlust wird mit Null angenommen.
Fall 1: Frequenzbereichsanalyse
Die Häufigkeitsanalyse von Betondämmen ist bei Wasserschutzprojekten von großer Bedeutung, vor allem in den folgenden Aspekten:
1. Bewertung der seismischen Leistung
Hohe Betondämme stehen normalerweise in erdbebengefährdeten Gebieten und ihre Erdbebensicherheit ist der Schlüssel zu ihrem sicheren Betrieb. Durch Frequenzanalyse können wir die dynamischen Reaktionseigenschaften des Staudamms bei Erdbeben verstehen und seine Erdbebensicherheit bewerten. Mithilfe einer Frequenzanalyse können beispielsweise die Eigenfrequenzen und Schwingungsarten eines Staudamms bei Erdbeben ermittelt und so seine seismische Leistung bewertet werden3.
2. Dynamische Charakteristikanalyse
Durch eine Frequenzanalyse können die dynamischen Eigenschaften des Damms, einschließlich Eigenfrequenz, Schwingungsmodus und Dämpfungsverhältnis, aufgedeckt werden. Diese dynamischen Eigenschaften sind entscheidend für das Verständnis der dynamischen Reaktion und des Verhaltens des Damms. Mithilfe der Frequenzanalyse können beispielsweise die Änderungen der Eigenfrequenz des Damms bei unterschiedlichen Wasserständen und Belastungsbedingungen verstanden und so seine dynamische Stabilität bewertet werden.
- Die folgende Abbildung zeigt die ersten 4 Vibrationsmodi von Koyna
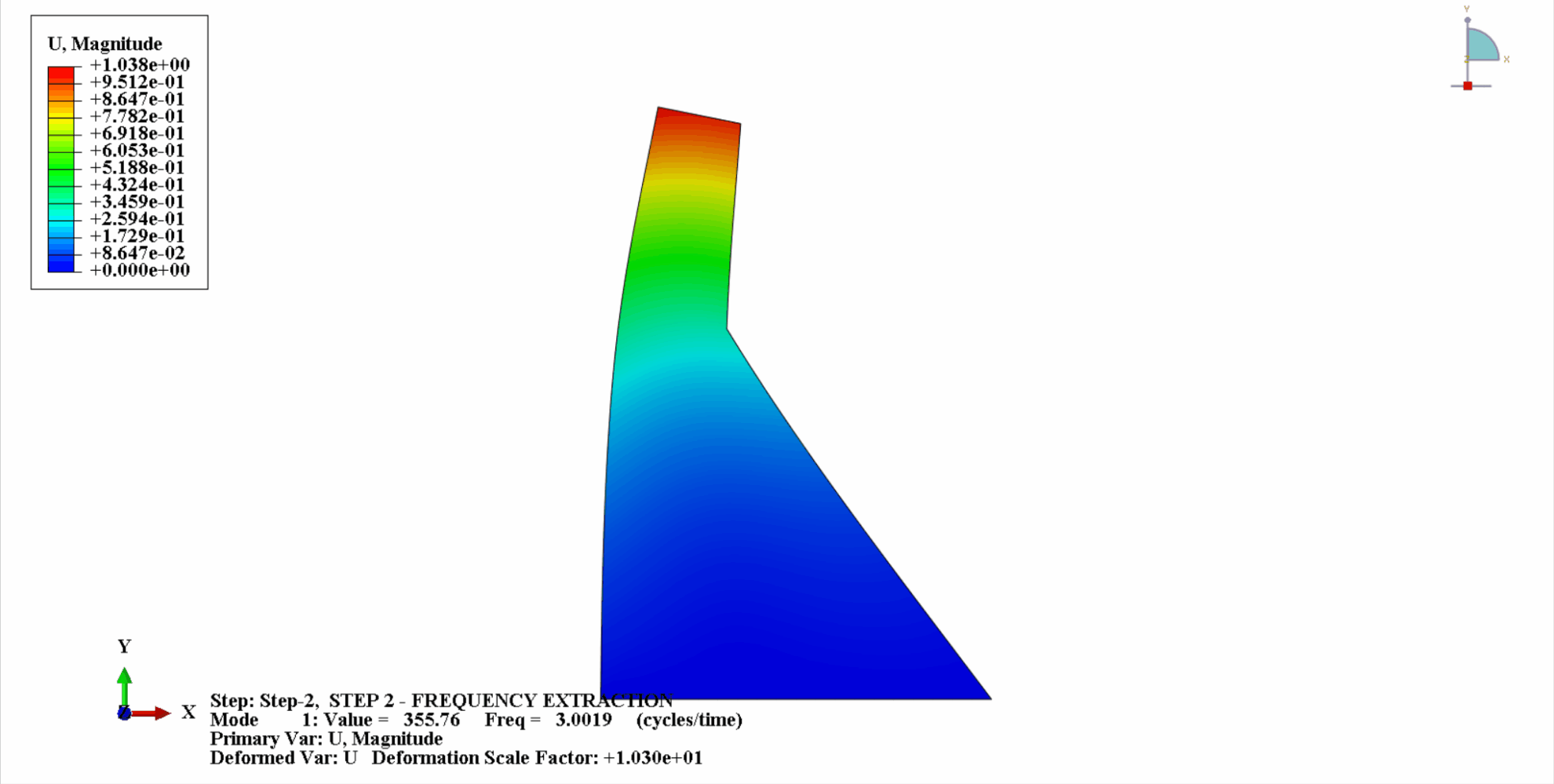
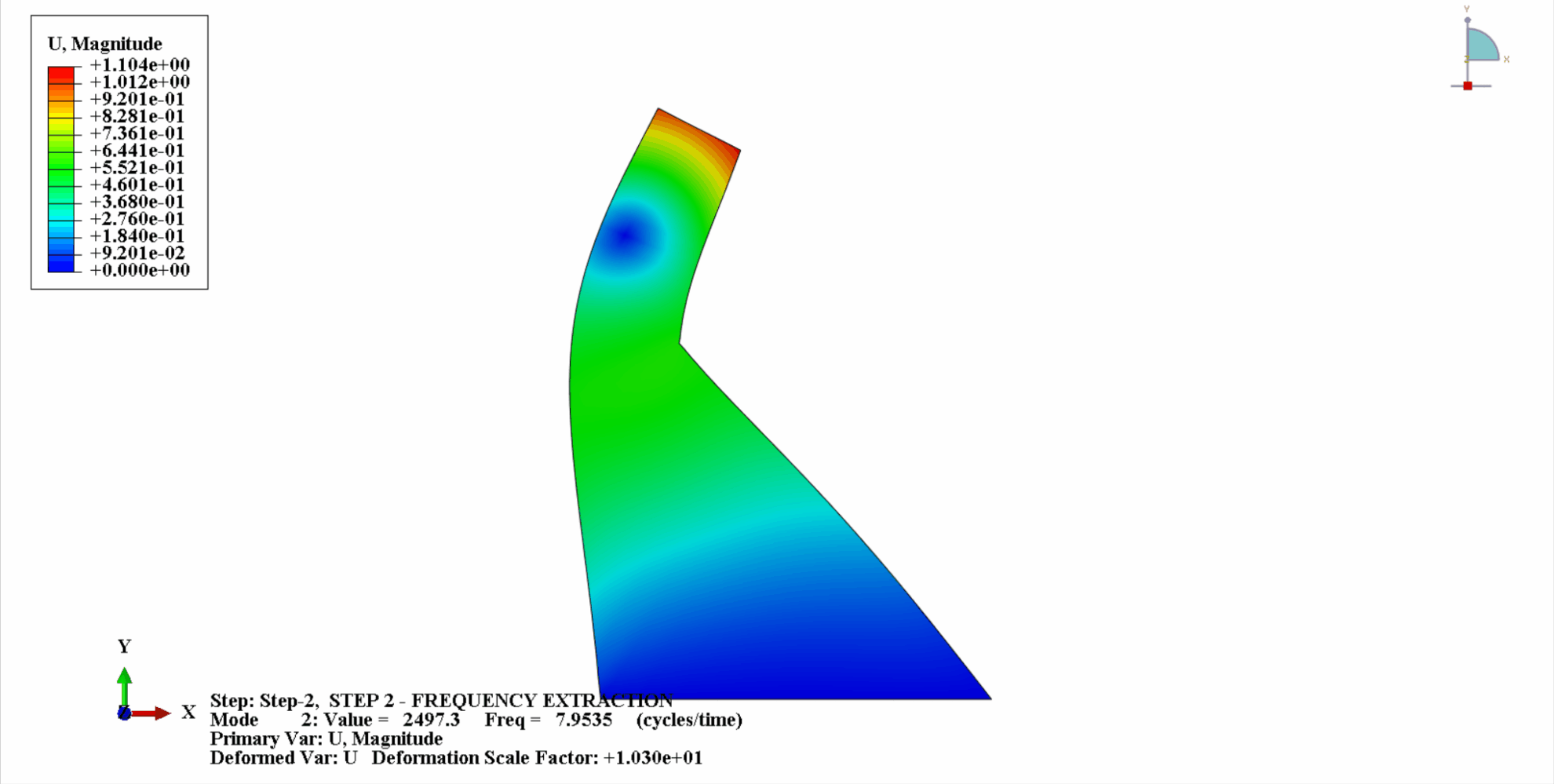
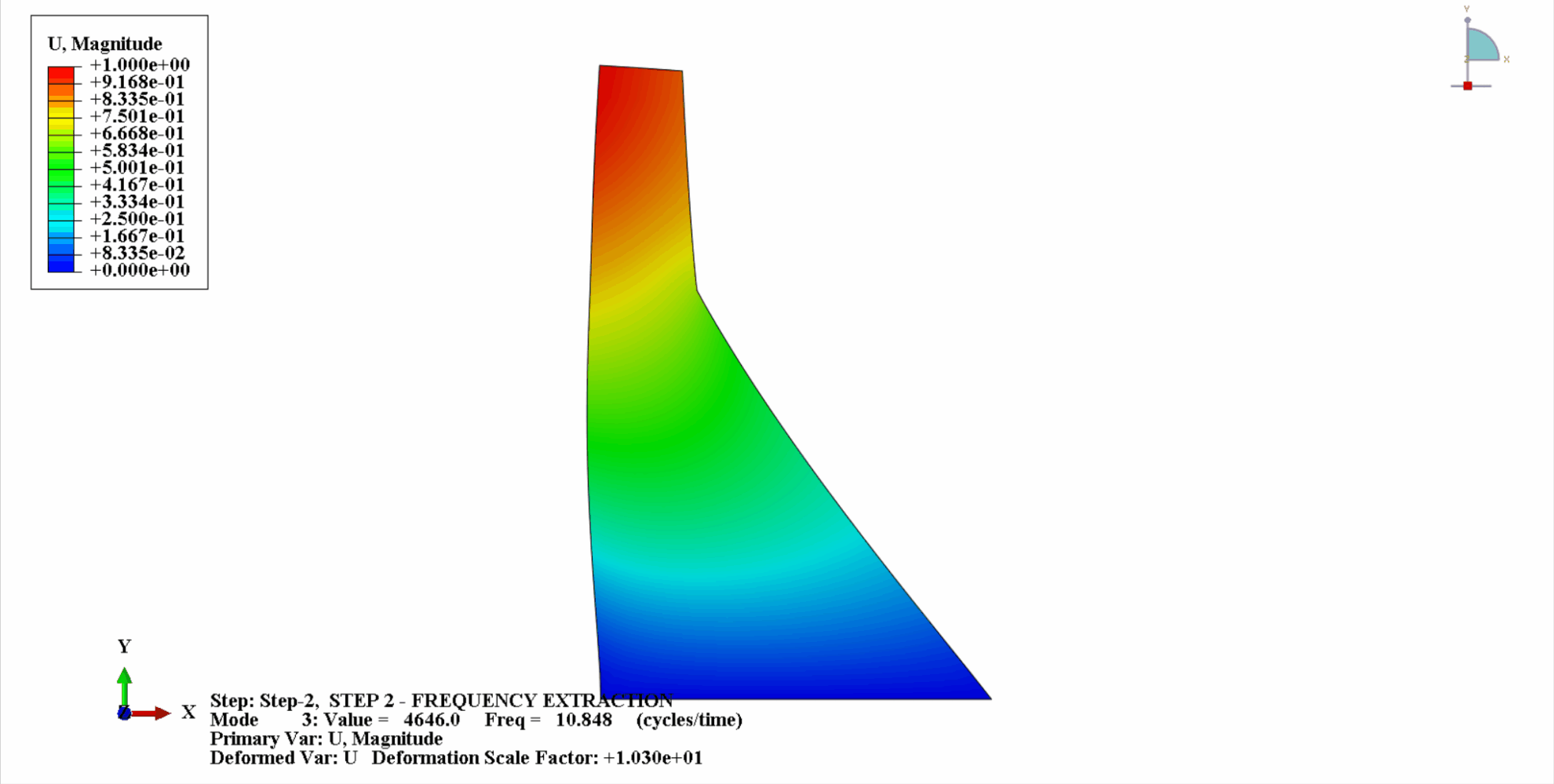
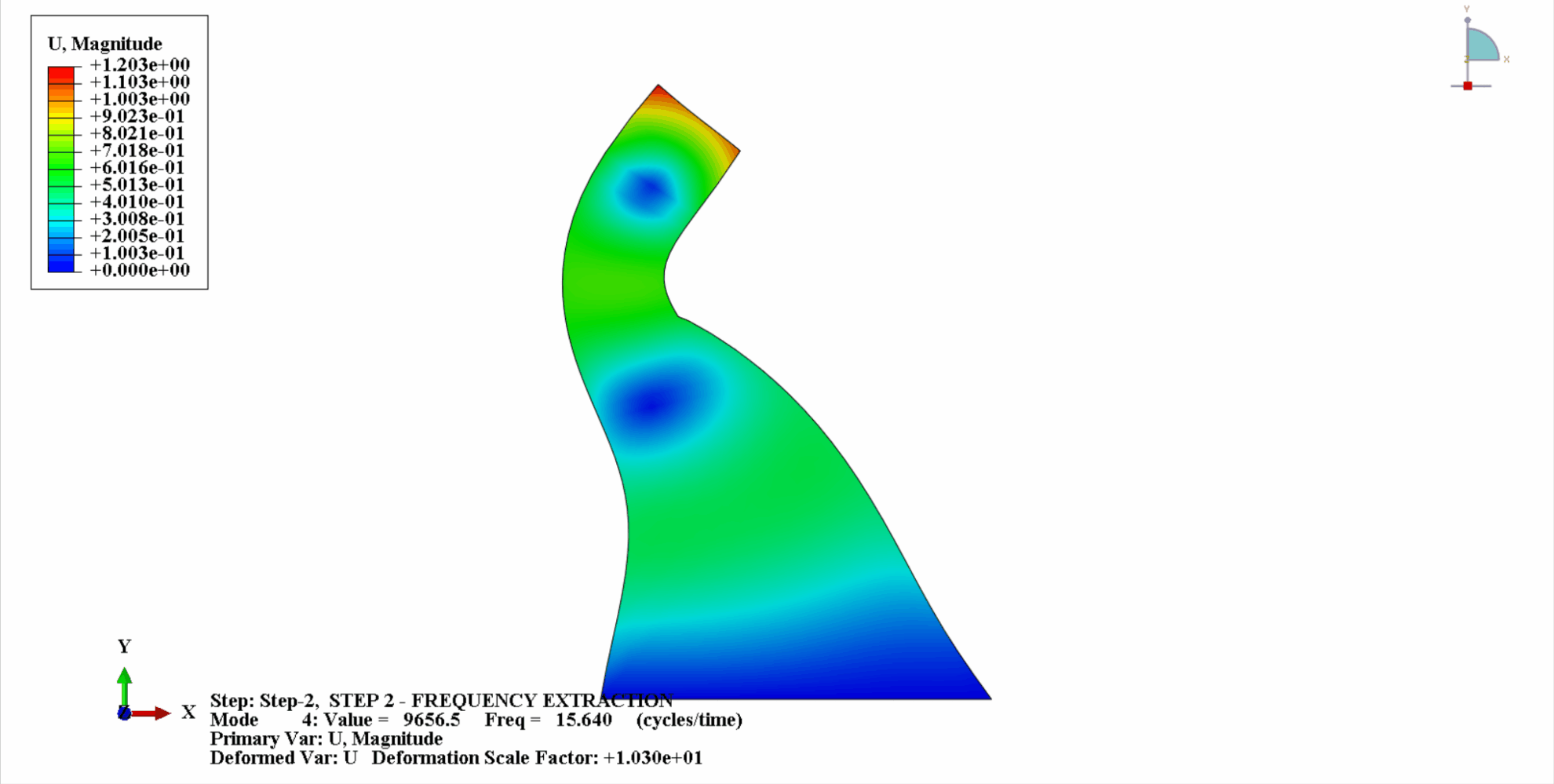
- Die folgende Tabelle zeigt den Vergleich der Eigenfrequenzen: Es ist ersichtlich, dass die Berechnungsergebnisse in diesem Beispiel mit den Berechnungen von Chopra übereinstimmen und der Berechnungsfehler in einem akzeptablen Rahmen liegt.
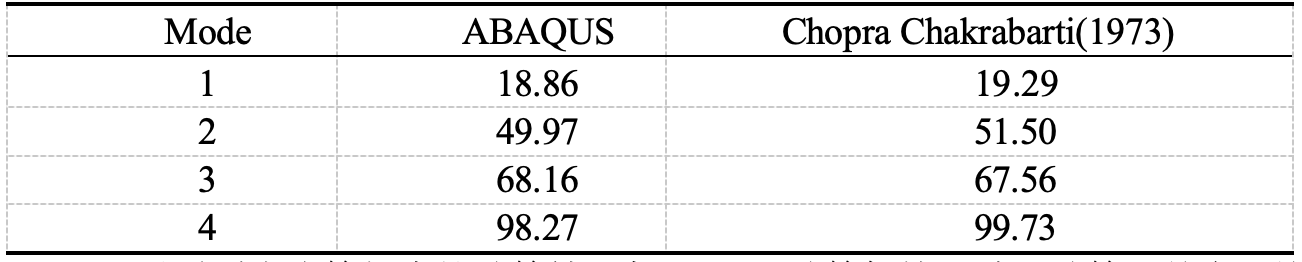
Es ist ersichtlich, dass die Berechnungsergebnisse in diesem Beispiel mit Chopras Berechnung übereinstimmen und der Berechnungsfehler innerhalb eines akzeptablen Bereichs liegt.
Fall 3: Analyse der seismischen Reaktion – Berücksichtigung des hydrodynamischen Drucks
Bei der Erdbebenanalyse von Betonstaudämmen liegt der Schwerpunkt auf den relativen Daten zwischen der Staudammkrone und der Staudammglocke, wie z. B. relativen Verschiebungsdaten, relativen Geschwindigkeitsdaten und relativen Beschleunigungsdaten.
* Unten sehen Sie die Zeitverlaufskurve der relativen Verschiebung von Dammkrone und Dammglocke entlang des Flusses:
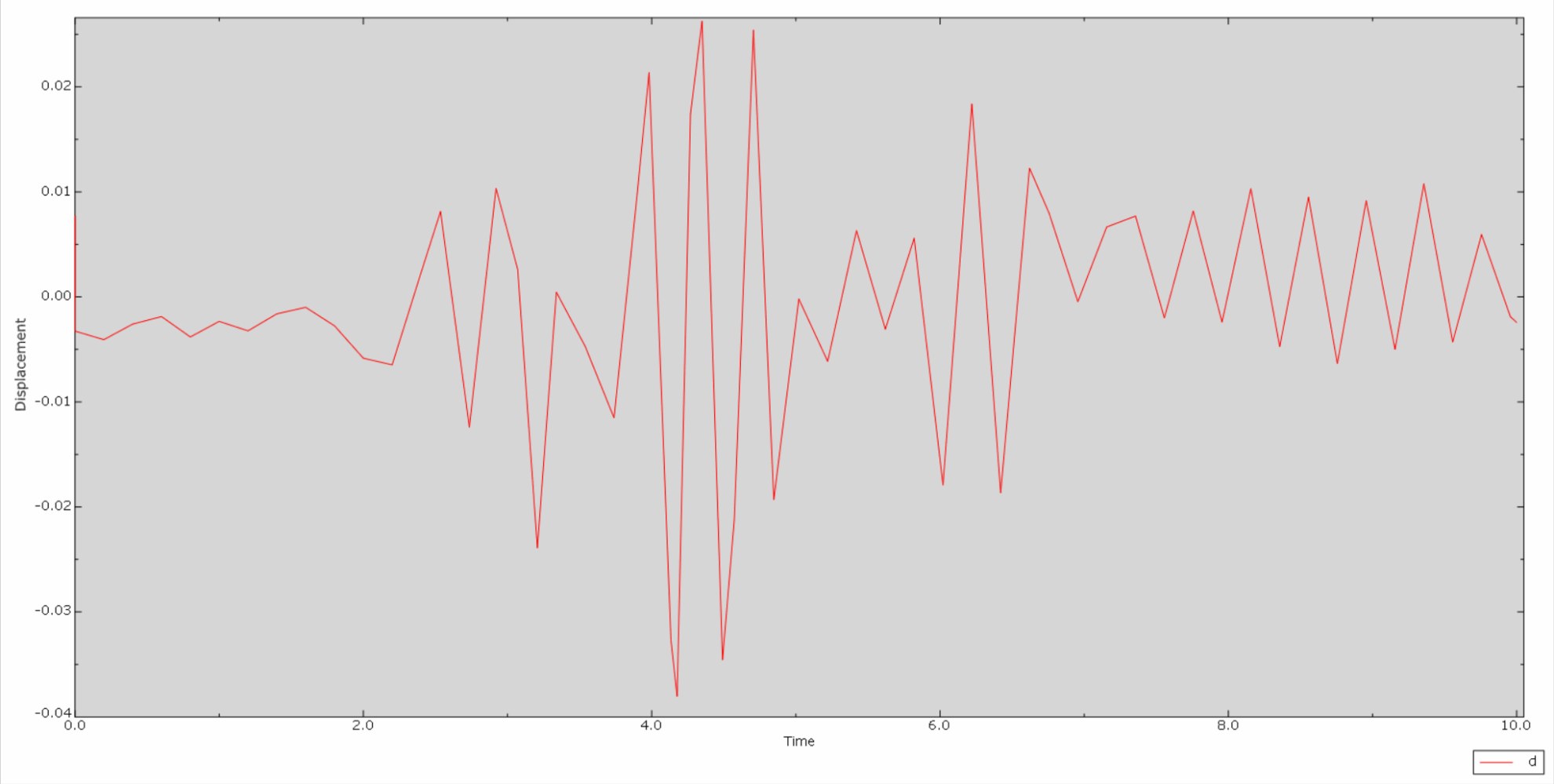
*Dann ist die relative Geschwindigkeits-Zeitverlaufskurve von Dammkrone und Dammglocke:
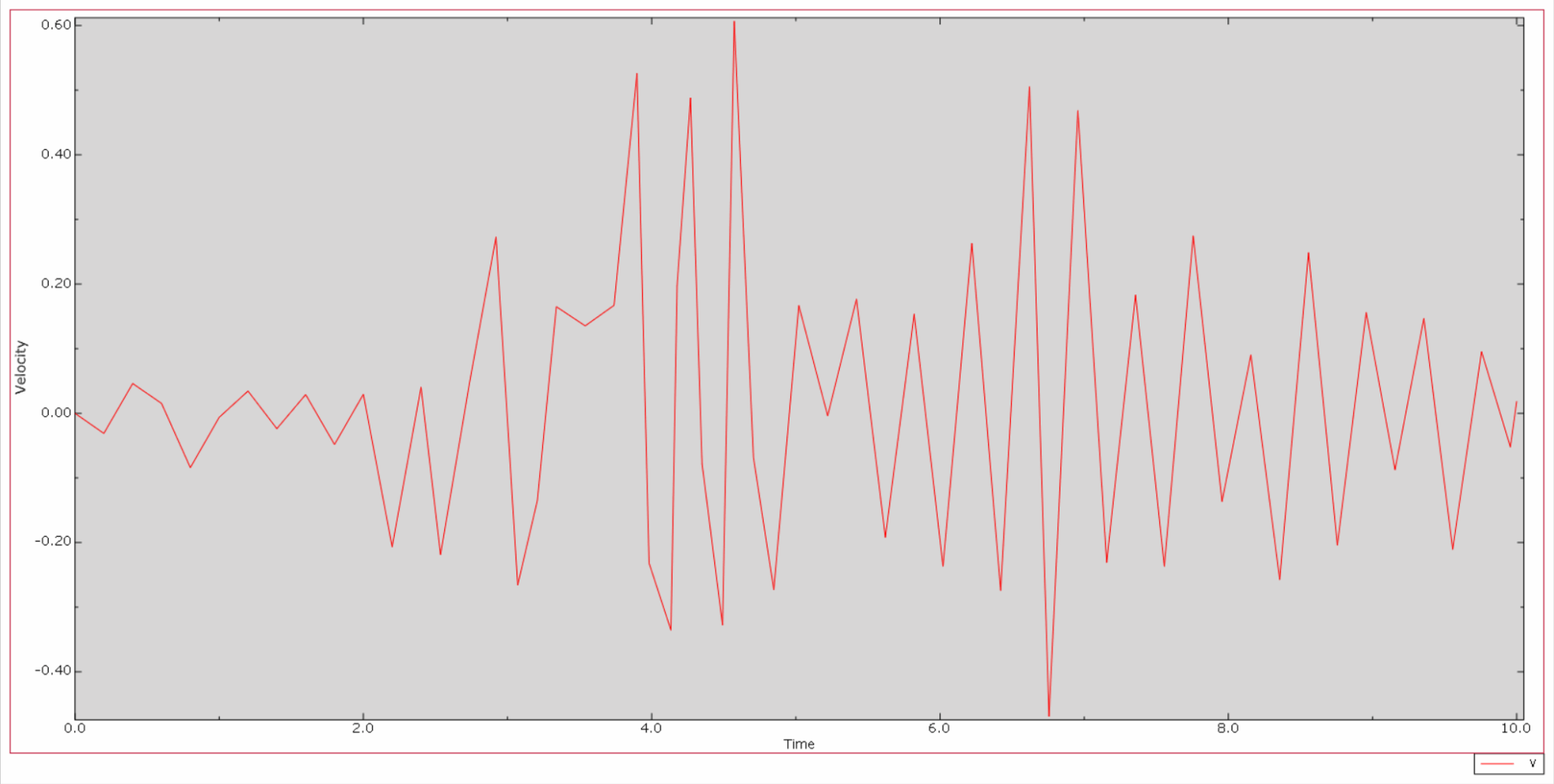
*Dann ergibt sich folgende relative Beschleunigungs-Zeit-Verlaufskurve von Dammkrone und Dammglocke:
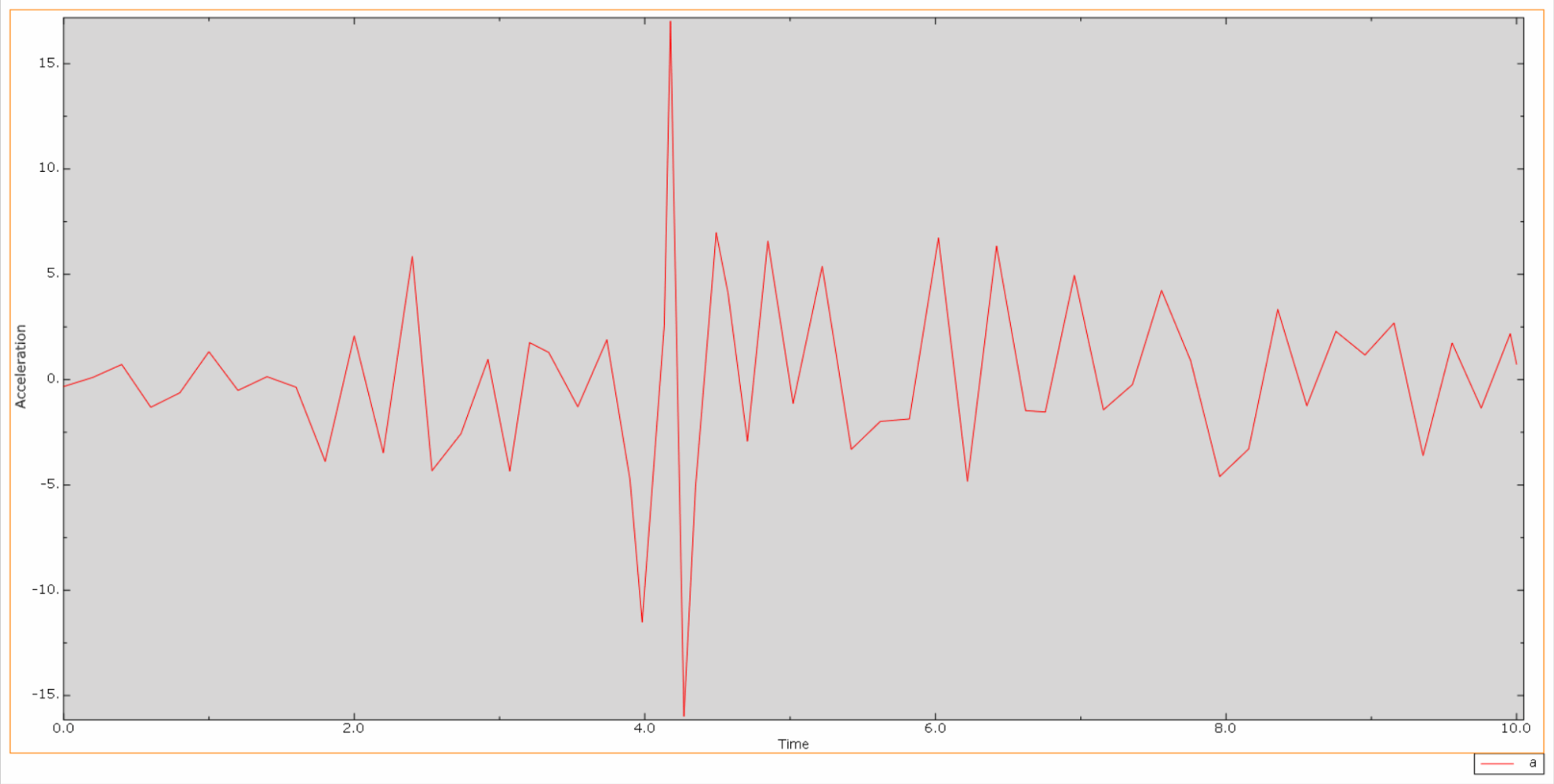
Unter der Einwirkung eines Erdbebens befindet sich das Material des Betondamms in einem zyklischen Zug-Druck-Zustand und der Beton wird beschädigt. Nachfolgend sehen Sie ein Wolkendiagramm der Zugschäden am Dammkörper zu verschiedenen Zeitpunkten.
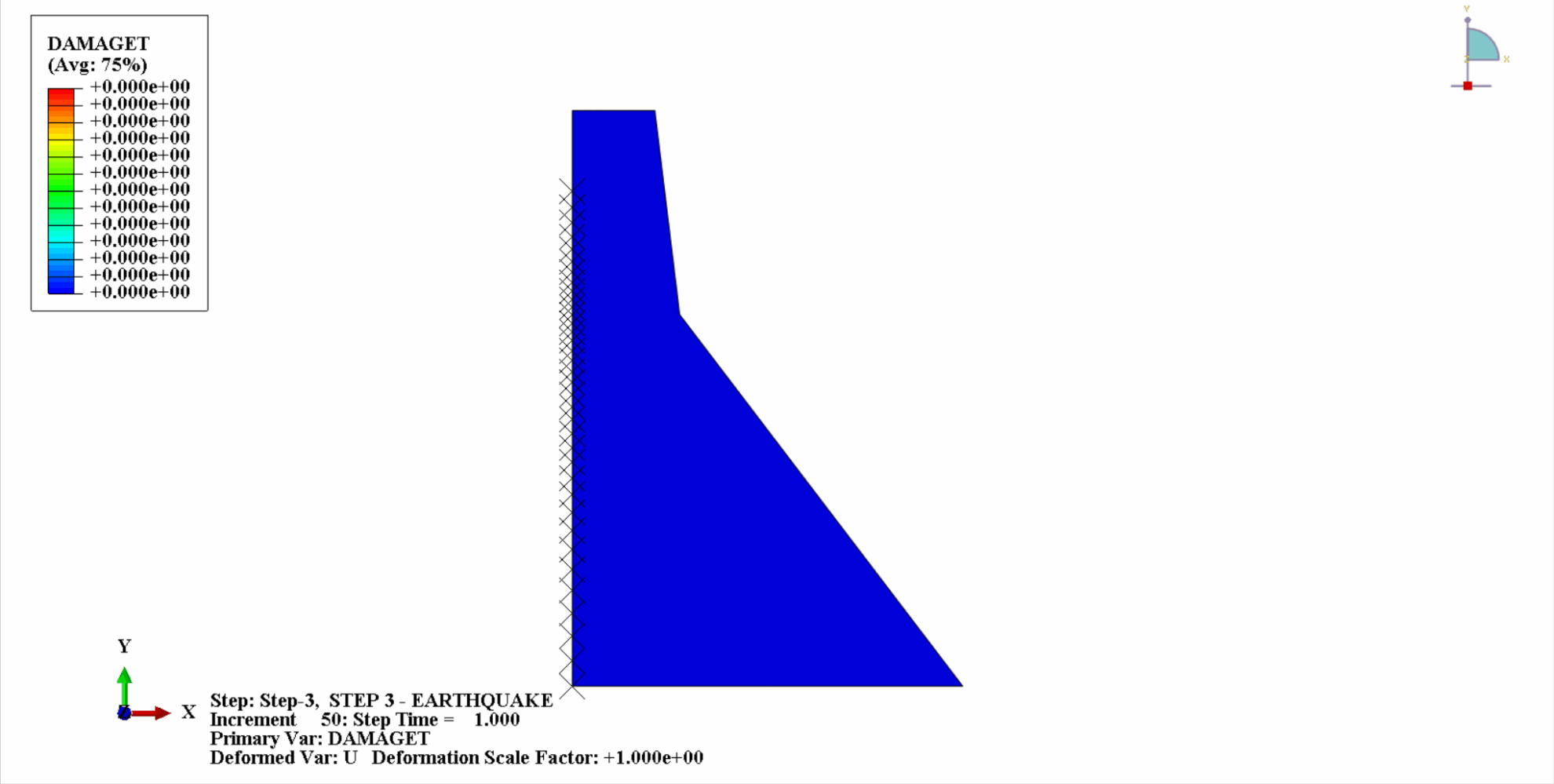
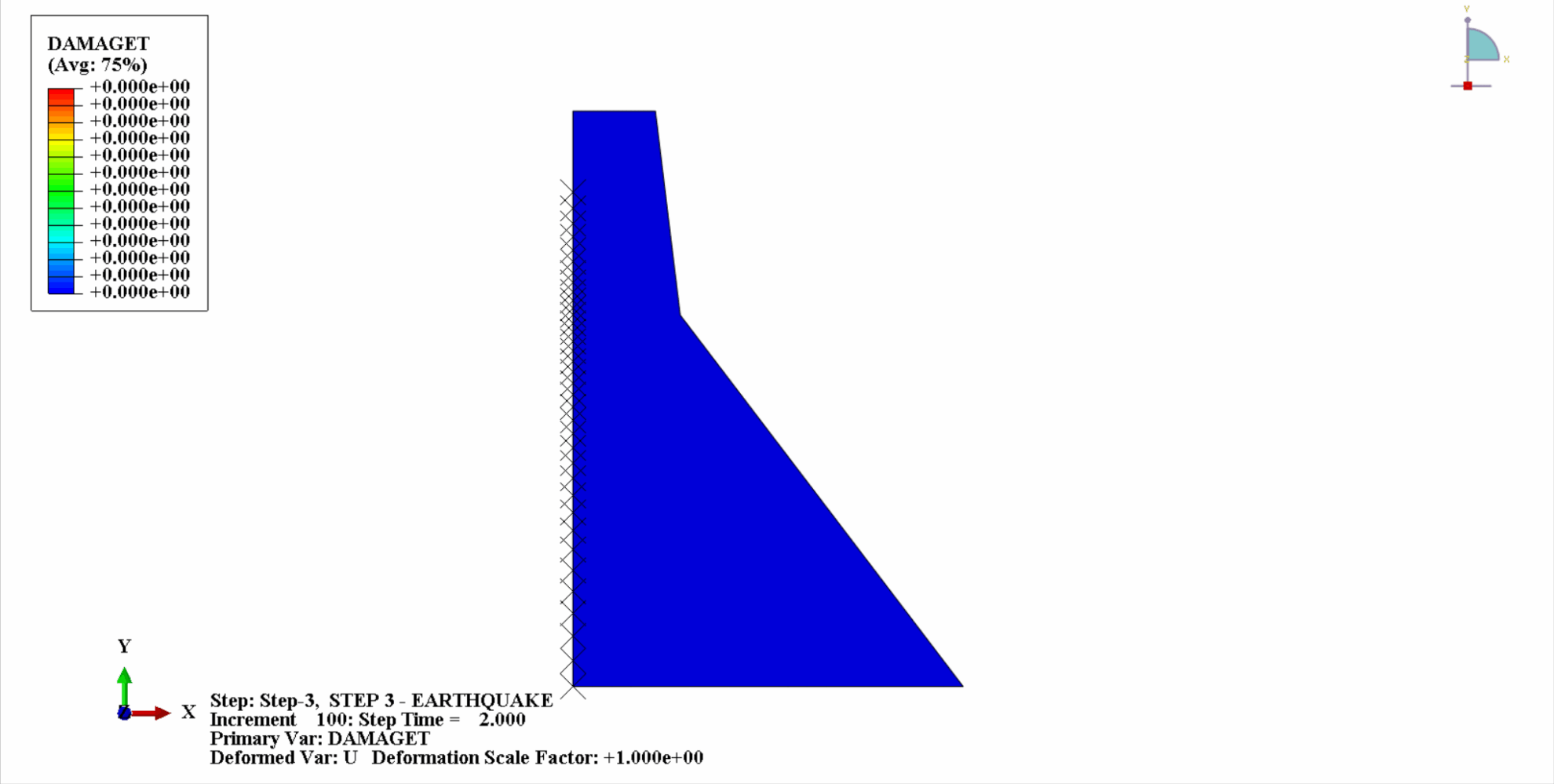
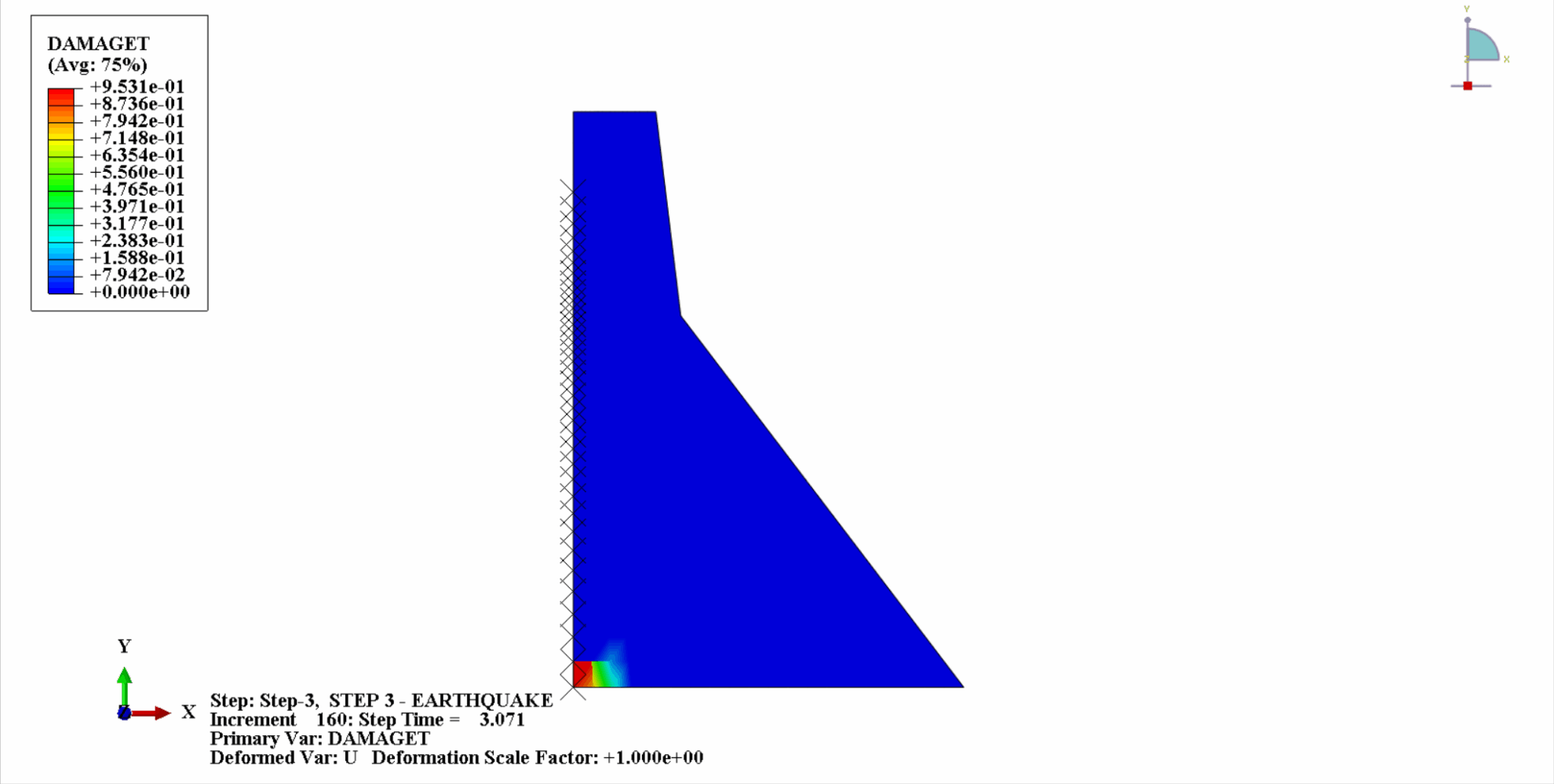
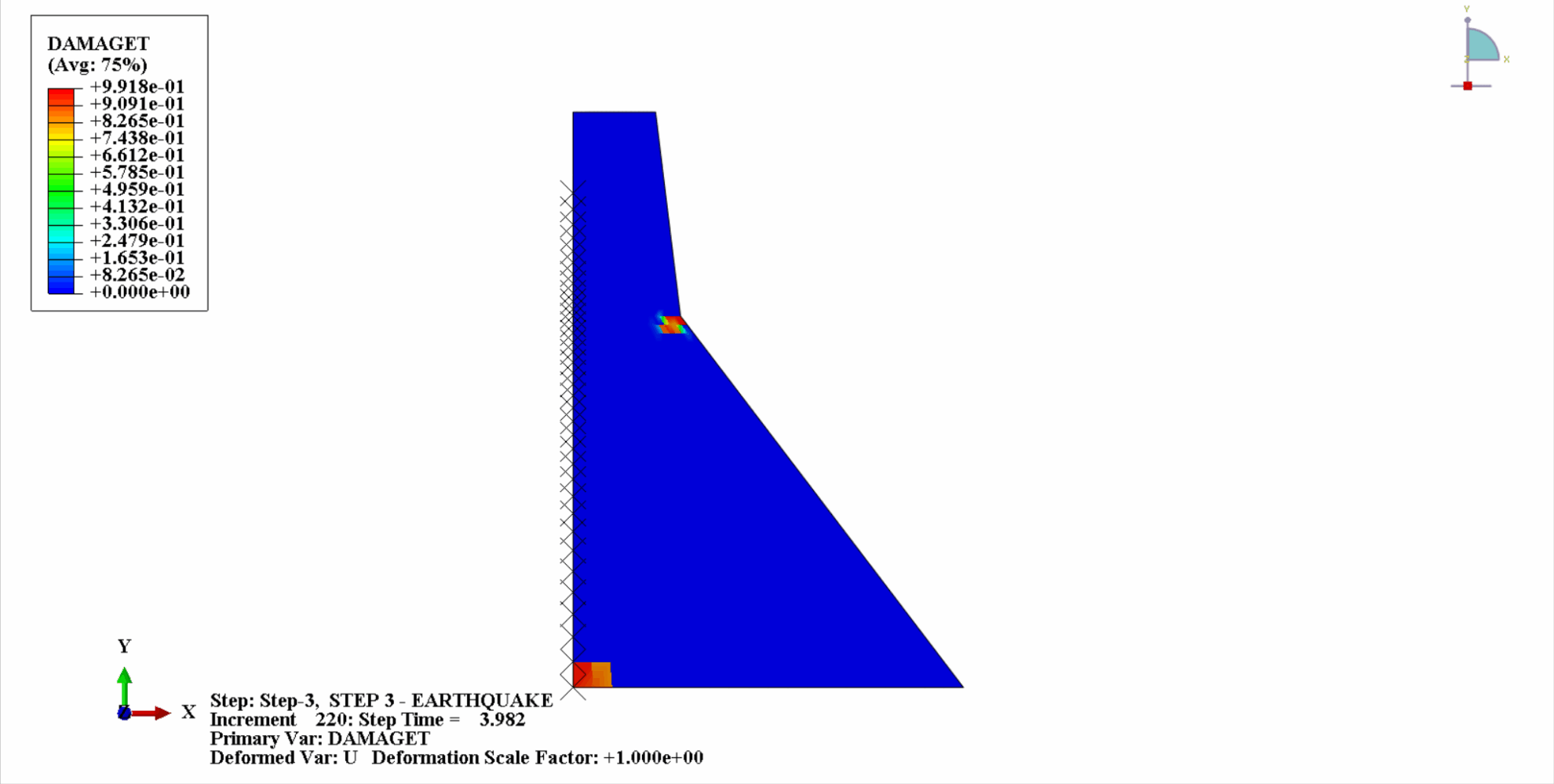
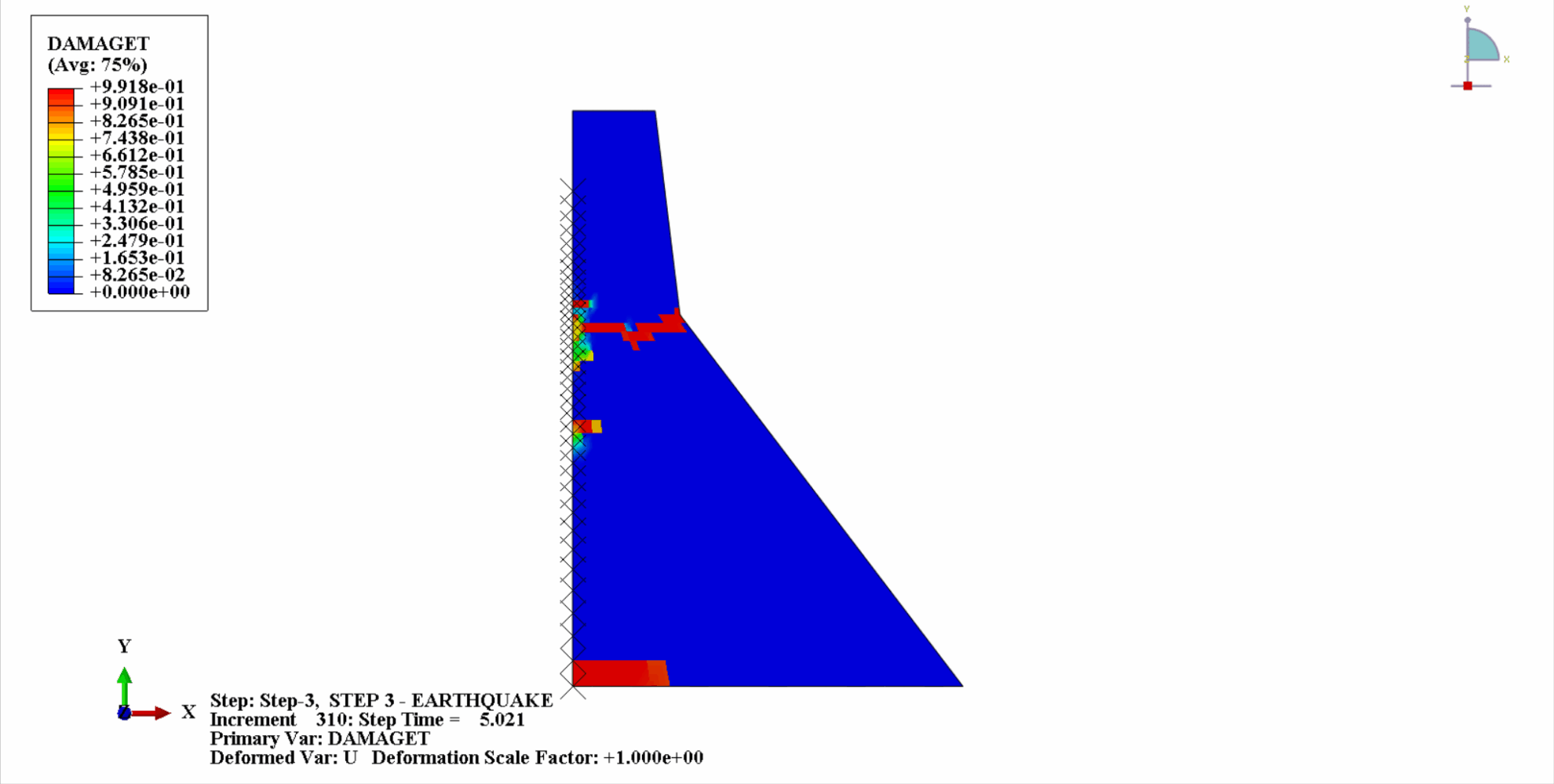
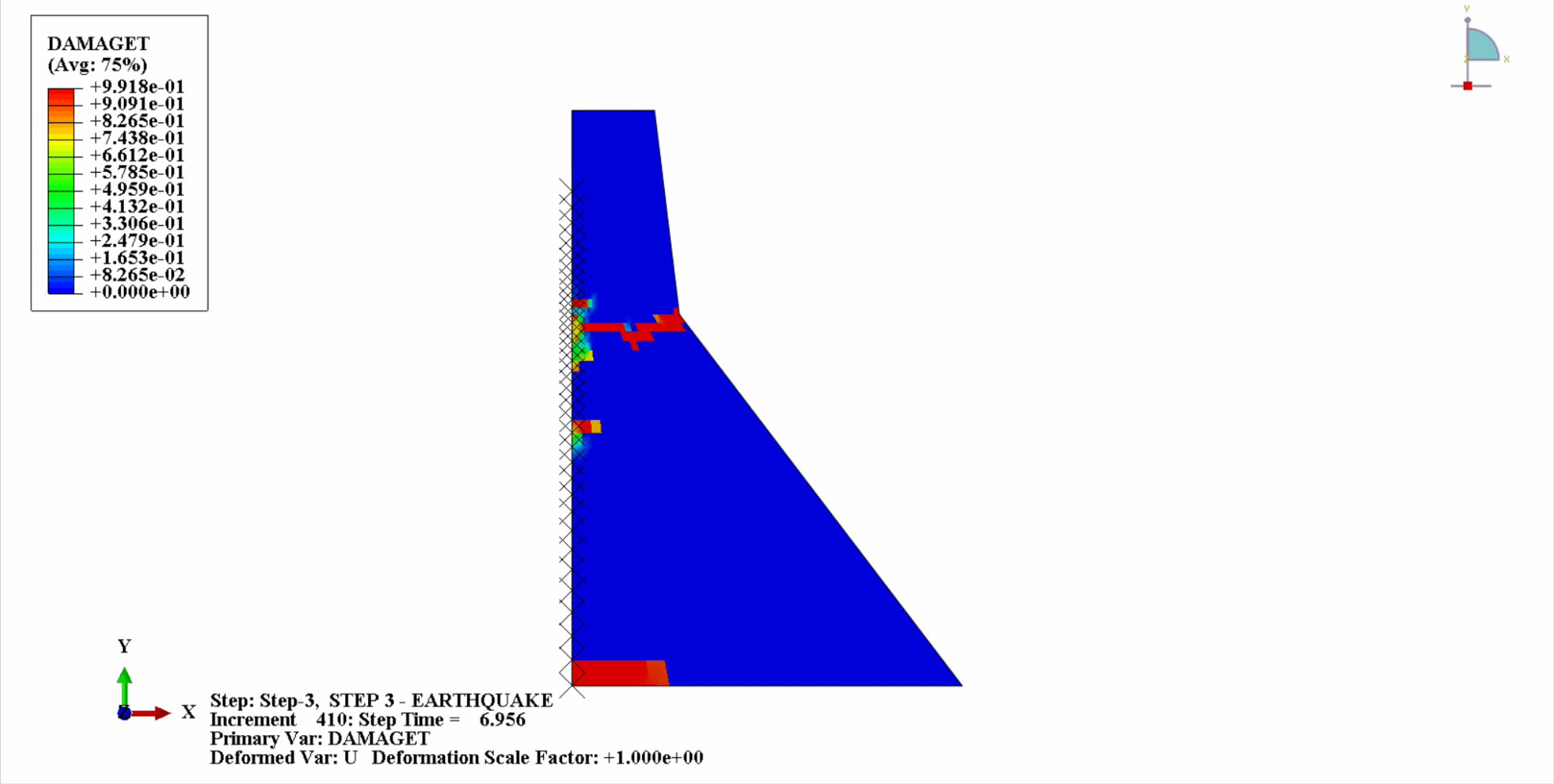
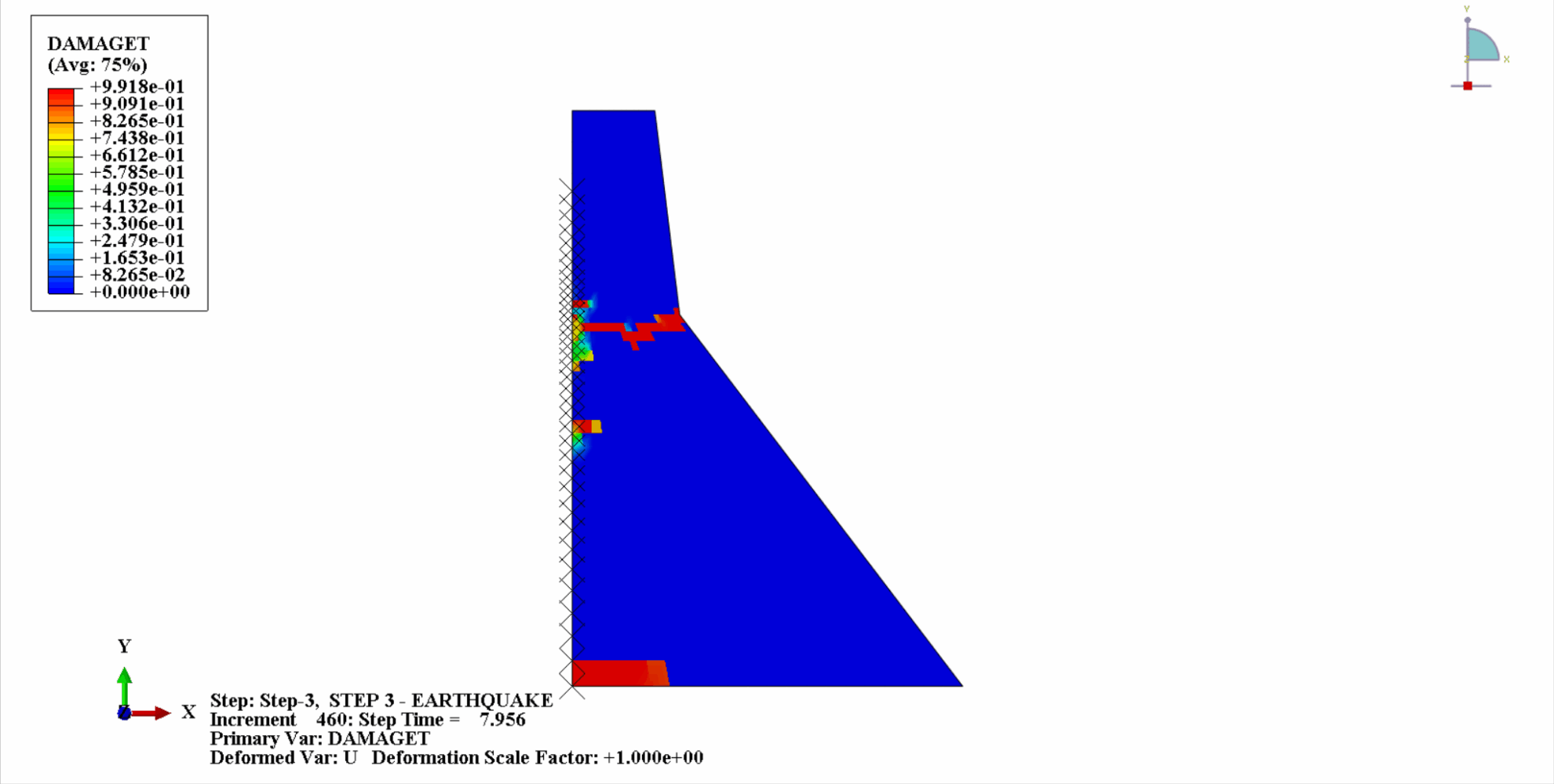
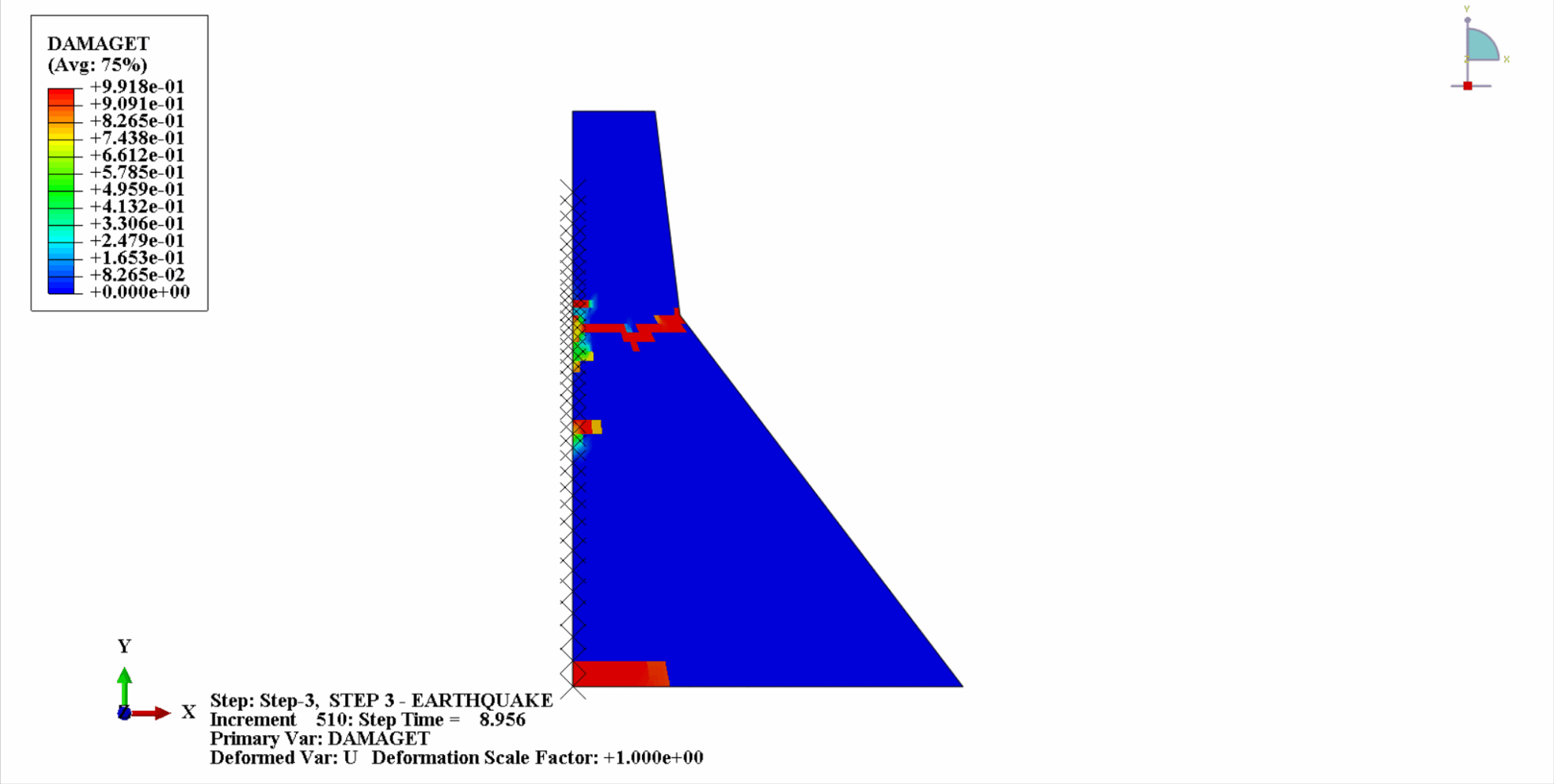
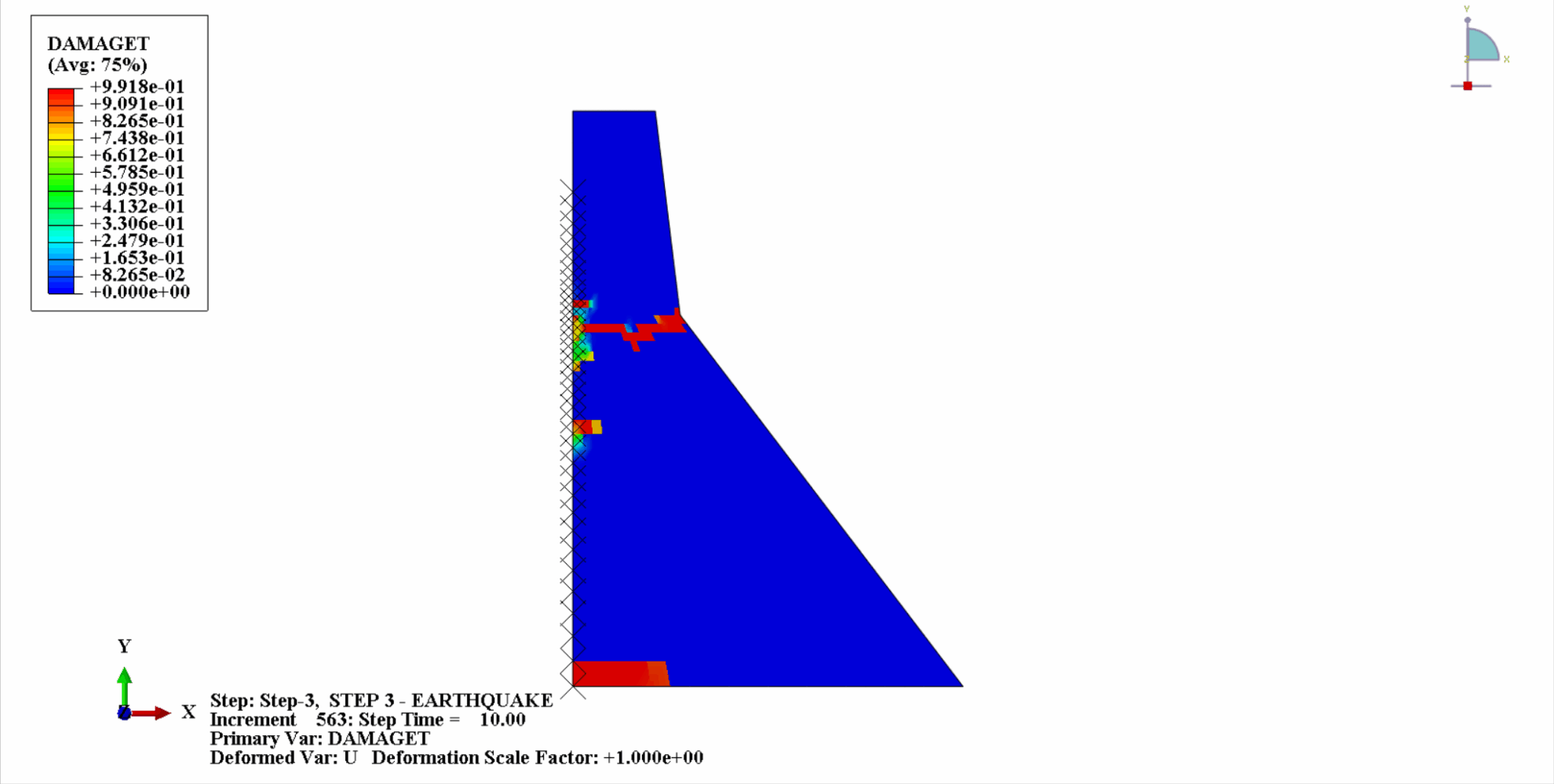
Es ist ersichtlich, dass sich mit zunehmender Zeit die Zugschäden am Dammbeton allmählich anhäufen. Im letzten Moment des Erdbebens erreicht der Schaden seinen Höhepunkt. Der Zugschadensbereich des Betondamms konzentriert sich hauptsächlich auf die Dammmitte und die stromaufwärts und stromabwärts gelegenen Falthänge des Dammkörpers.