Command Palette
Search for a command to run...
VASP-Hybridfunktionalberechnung Der Zustandsdichte Und Energiebänder Von Silizium
Vienna Ab initio Simulation Package (VASP) Es handelt sich um ein Computerprogramm zur Materialmodellierung auf atomarer Ebene ausgehend von Grundprinzipien, wie etwa Berechnungen der elektronischen Struktur und quantenmechanische Molekulardynamik.
VASP eignet sich zur Berechnung von Näherungslösungen der Vielteilchen-Schrödingergleichung. Es deckt eine Vielzahl von Rechenmethoden ab, darunter das Lösen der Kohn-Sham-Gleichung im Rahmen der Dichtefunktionaltheorie (DFT) und die Behandlung der Roothaan-Gleichung in der Hartree-Fock-Näherung (HF). Eine weitere Innovation von VASP besteht darin, dass es die Hartree-Fock-Methode mit der Dichtefunktionaltheorie zu einer hybriden Funktionalmethode integriert, die Forschern flexiblere Berechnungsmöglichkeiten bietet. Darüber hinaus sind in VASP Green'sche Funktionsmethoden (GW-Quasiteilchen und ACFDT-RPA) und die Vielteilchen-Störungstheorie (Møller-Plesset zweiter Ordnung) verfügbar.
In VASP werden zentrale Größen wie einzelne Elektronenorbitale, Elektronenladungsdichte und lokales Potenzial mithilfe von Basissätzen ebener Wellen dargestellt. Die Wechselwirkungen zwischen Elektronen und Ionen werden mithilfe von Normerhaltungs- oder ultraweichen Pseudopotentialen oder projektorgestützten Wellenmethoden beschrieben.
Zur Bestimmung des elektronischen Grundzustands nutzt VASP effiziente iterative Matrixdiagonalisierungstechniken wie die Methode der Residualminimierung mit direkter Inversion des iterierten Subraums (RMM-DIIS) oder den Block-Davidson-Algorithmus. Diese werden mit effizienten Broyden- und Pulay-Dichtemischschemata kombiniert, um die selbstkonsistente Schleife zu beschleunigen.
Einführung in das Tutorial
In diesem Tutorial lernen Sie, wie Sie Silizium-Energiebänder mithilfe von Hybridfunktionalen berechnen. Dies ähnelt dem vorherigen Tutorial (VASP-Tutorial für den Einstieg: Berechnung der Zustandsdichte und Bandbreiten in Silizium), kann das Hybridfunktional die Energiebänder und die Zustandsdichte des Materials mit der richtigen Bandlücke berechnen, erfordert jedoch mehr Rechenressourcen, sodass diesmal die GPU zur Demonstration verwendet wird.
In diesem Lernprogramm lernen Sie, die für VASP-Hybridfunktionsberechnungen erforderlichen INCAR- und KPOITNS-Daten zu generieren.
Vorheriges Tutorial (VASP-Tutorial für den Einstieg: Berechnung der Zustandsdichte und Bandbreiten in Silizium) enthält 4 Schritte. Die Berechnung dieses Hybridfunktionals erfordert nur einen Schritt (die Strukturoptimierung wird übersprungen), um die Zustandsdichte und das Energieband von Silizium zu erhalten.
Vorbereiten von Eingabedateien
Dieses Tutorial erfordert die Vorbereitung von vier Dateien: INCAR, POSCAR, KPOINTS und POTCAR.
INCAR
Global Parameters
ENCUT = 300 (波函数截断能量)
PREC = Normal (精度设置)
LWAVE = .TRUE. (保存波函数)
LCHARG = .TRUE. (保存电荷)
ADDGRID= .TRUE. (增加格点加速收敛)
Static Calculation
ISMEAR = 0 (高斯占据数)
SIGMA = 0.1 (高斯展宽)
LORBIT = 11 (输出 DOSCAR 和 PROCAR)
NELM = 60 (最大电子步)
EDIFF = 1E-08 (电子步收敛判据)
HSE06 Calculation
LHFCALC= T (启动杂化泛函计算)
AEXX = 0.25 (杂化比例 0.25)
HFSCREEN= 0.2 (杂化屏蔽参数 0.2)
ALGO = ALL (最优化算法)
TIME = 0.4 (最优化算法步长)
PRECFOCK= N (FFT 精度)
POSCAR
Si #(体系名称)
1.0 #(放大系数 下面 3 行对应 3 个晶格矢量 )
0.0 2.75 2.75
2.75 0.0 2.75
2.75 2.75 0.0
Si #(元素)
2 #(对应元素原子数)
Direct #(采用分数坐标,下列为 2 个原子的分数坐标)
0 0 0
0.25 0.25 0.25
KPUNKTE
0.060 5 5 5 10 0.060 83 6 19 6 20 16 13 9 # Parameters to Generate KPOINTS (Do NOT Edit This Line)
93
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.20000000000000 0.00000000000000 0.00000000000000 8
0.40000000000000 0.00000000000000 0.00000000000000 8
0.20000000000000 0.20000000000000 0.00000000000000 6
0.40000000000000 0.20000000000000 0.00000000000000 24
-0.40000000000000 0.20000000000000 0.00000000000000 24
-0.20000000000000 0.20000000000000 0.00000000000000 12
0.40000000000000 0.40000000000000 0.00000000000000 6
-0.40000000000000 0.40000000000000 0.00000000000000 12
-0.40000000000000 0.40000000000000 0.20000000000000 24 (以上为 scf 点位)
0.00000000000000 0.00000000000000 0.00000000000000 0 (以下为能带点位)
0.02777777777778 0.00000000000000 0.02777777777778 0
0.05555555555556 0.00000000000000 0.05555555555556 0
0.08333333333333 0.00000000000000 0.08333333333333 0
0.11111111111111 0.00000000000000 0.11111111111111 0
0.13888888888889 0.00000000000000 0.13888888888889 0
0.16666666666667 0.00000000000000 0.16666666666667 0
0.19444444444444 0.00000000000000 0.19444444444444 0
0.22222222222222 0.00000000000000 0.22222222222222 0
0.25000000000000 0.00000000000000 0.25000000000000 0
0.27777777777778 0.00000000000000 0.27777777777778 0
0.30555555555556 0.00000000000000 0.30555555555556 0
0.33333333333333 0.00000000000000 0.33333333333333 0
0.36111111111111 0.00000000000000 0.36111111111111 0
0.38888888888889 0.00000000000000 0.38888888888889 0
0.41666666666667 0.00000000000000 0.41666666666667 0
0.44444444444444 0.00000000000000 0.44444444444444 0
0.47222222222222 0.00000000000000 0.47222222222222 0
0.50000000000000 0.00000000000000 0.50000000000000 0
0.50000000000000 0.00000000000000 0.50000000000000 0
0.52500000000000 0.05000000000000 0.52500000000000 0
0.55000000000000 0.10000000000000 0.55000000000000 0
0.57500000000000 0.15000000000000 0.57500000000000 0
0.60000000000000 0.20000000000000 0.60000000000000 0
0.62500000000000 0.25000000000000 0.62500000000000 0
0.37500000000000 0.37500000000000 0.75000000000000 0
0.35526315789474 0.35526315789474 0.71052631578947 0
0.33552631578947 0.33552631578947 0.67105263157895 0
0.31578947368421 0.31578947368421 0.63157894736842 0
0.29605263157895 0.29605263157895 0.59210526315789 0
0.27631578947368 0.27631578947368 0.55263157894737 0
0.25657894736842 0.25657894736842 0.51315789473684 0
0.23684210526316 0.23684210526316 0.47368421052632 0
0.21710526315789 0.21710526315789 0.43421052631579 0
0.19736842105263 0.19736842105263 0.39473684210526 0
0.17763157894737 0.17763157894737 0.35526315789474 0
0.15789473684211 0.15789473684211 0.31578947368421 0
0.13815789473684 0.13815789473684 0.27631578947368 0
0.11842105263158 0.11842105263158 0.23684210526316 0
0.09868421052632 0.09868421052632 0.19736842105263 0
0.07894736842105 0.07894736842105 0.15789473684211 0
0.05921052631579 0.05921052631579 0.11842105263158 0
0.03947368421053 0.03947368421053 0.07894736842105 0
0.01973684210526 0.01973684210526 0.03947368421053 0
0.00000000000000 0.00000000000000 0.00000000000000 0
0.00000000000000 0.00000000000000 0.00000000000000 0
0.03333333333333 0.03333333333333 0.03333333333333 0
0.06666666666667 0.06666666666667 0.06666666666667 0
0.10000000000000 0.10000000000000 0.10000000000000 0
0.13333333333333 0.13333333333333 0.13333333333333 0
0.16666666666667 0.16666666666667 0.16666666666667 0
0.20000000000000 0.20000000000000 0.20000000000000 0
0.23333333333333 0.23333333333333 0.23333333333333 0
0.26666666666667 0.26666666666667 0.26666666666667 0
0.30000000000000 0.30000000000000 0.30000000000000 0
0.33333333333333 0.33333333333333 0.33333333333333 0
0.36666666666667 0.36666666666667 0.36666666666667 0
0.40000000000000 0.40000000000000 0.40000000000000 0
0.43333333333333 0.43333333333333 0.43333333333333 0
0.46666666666667 0.46666666666667 0.46666666666667 0
0.50000000000000 0.50000000000000 0.50000000000000 0
0.50000000000000 0.50000000000000 0.50000000000000 0
0.50000000000000 0.47916666666667 0.52083333333333 0
0.50000000000000 0.45833333333333 0.54166666666667 0
0.50000000000000 0.43750000000000 0.56250000000000 0
0.50000000000000 0.41666666666667 0.58333333333333 0
0.50000000000000 0.39583333333333 0.60416666666667 0
0.50000000000000 0.37500000000000 0.62500000000000 0
0.50000000000000 0.35416666666667 0.64583333333333 0
0.50000000000000 0.33333333333333 0.66666666666667 0
0.50000000000000 0.31250000000000 0.68750000000000 0
0.50000000000000 0.29166666666667 0.70833333333333 0
0.50000000000000 0.27083333333333 0.72916666666667 0
0.50000000000000 0.25000000000000 0.75000000000000 0
0.50000000000000 0.25000000000000 0.75000000000000 0
0.50000000000000 0.21875000000000 0.71875000000000 0
0.50000000000000 0.18750000000000 0.68750000000000 0
0.50000000000000 0.15625000000000 0.65625000000000 0
0.50000000000000 0.12500000000000 0.62500000000000 0
0.50000000000000 0.09375000000000 0.59375000000000 0
0.50000000000000 0.06250000000000 0.56250000000000 0
0.50000000000000 0.03125000000000 0.53125000000000 0
0.50000000000000 0.00000000000000 0.50000000000000 0
POTCAR
Das System entspricht der pseudopotentiellen Kombination von Elementen, hier ist es das Pseudopotential von Si.
Schritte ausführen
Kommen wir nun zum praktischen Teil des Tutorials. Das Tutorial hat die erforderlichen Pakete vorbereitet, sodass Sie den Container direkt klonen können. Dieses Tutorial verwendet RTX 4090-Rechenressourcen, das Image der Version vasp 6.3.0-cuda11.8 und wird im Arbeitsbereich ausgeführt.
1. Klonen und starten Sie den Container
1.1 Warten Sie, bis der Container geladen ist, und klicken Sie dann auf „Arbeitsbereich öffnen“
1.2 Terminal öffnen
1.3 Geben Sie das wfl-Verzeichnis ein
cd tutorials/wfl
1.4 Laden Sie das vorbereitete Silizium-Pseudopotential in das wfl-Verzeichnis hoch
Hier können SieBeispieldatei der offiziellen WebsitePseudopotentielles POTCAR
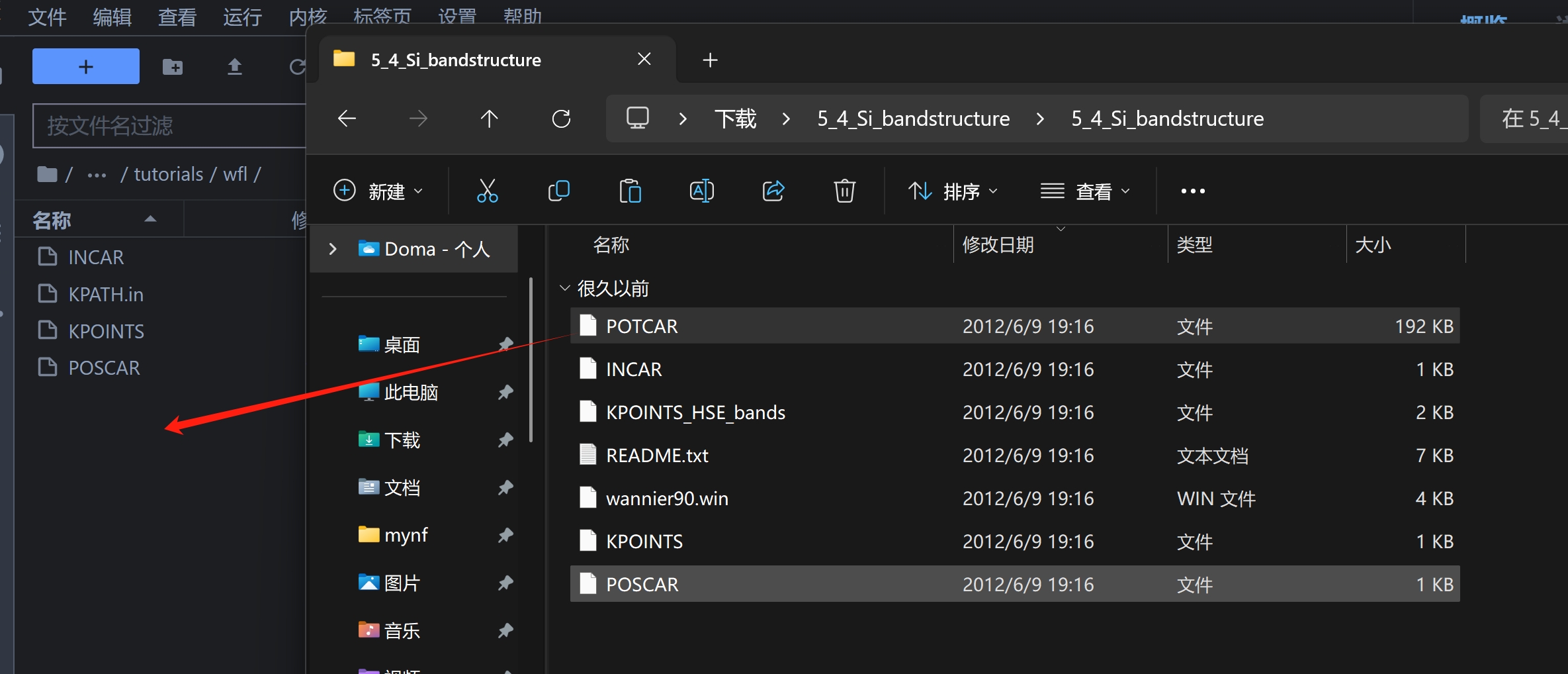
2. Führen Sie VASP aus
mpirun -n 1 vasp_std
3. Installieren Sie vaspkit
Zurück zum vorherigen Verzeichnis
cd ..
3.1 Python-Abhängigkeiten installieren
pip install numpy scipy matplotlib
3.2 Vaspkit konfigurieren
chmod 777 setupvk.sh
./setupvk.sh
source ~/.bashrc
cd tutorials
4. Datenverarbeitung mit vaspkit
4.1 Darstellung der Zustandsdichte und Banddiagramme
Geben Sie Folgendes in das wfl-Verzeichnis ein:
cd wfl
Geben Sie den Befehl zum Generieren von Zustandsdichtedaten ein:
vaspkit
111
1
Geben Sie den Befehl ein, um die Banddaten mit vaspkit zu verarbeiten und darzustellen:
vaspkit
252
2
Die Zustandsdichte und das Banddiagramm können wie folgt generiert werden:
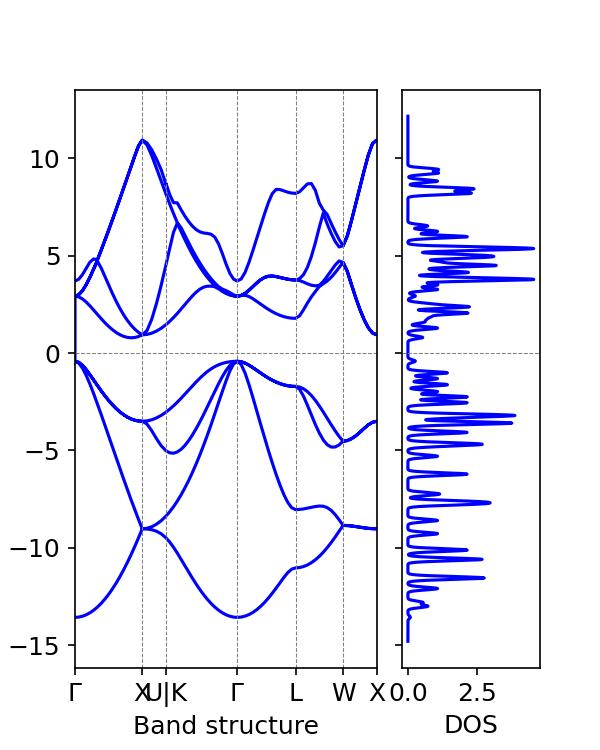
Verwenden wir vaspkit, um die Bandlücke anzuzeigen:
vaspkit
911
Daraus lässt sich schließen, dass die geschätzte Silizium-Bandlücke 1,2 eV beträgt, was nahe am typischen experimentellen Wert der Silizium-Bandlücke von 1,12 eV liegt.
Im vorherigen Tutorial ergaben DFT-Berechnungen mit vaspkit eine Bandlücke von 0,6133 eV, die weit vom experimentellen Wert entfernt ist.
Daher können Hybridfunktionale die Bandlücke von Materialien genauer berechnen, sie erfordern jedoch mehr Rechenressourcen.
KI mit KI entwickeln
Von der Idee bis zum Launch – beschleunigen Sie Ihre KI-Entwicklung mit kostenlosem KI-Co-Coding, sofort einsatzbereiter Umgebung und bestem GPU-Preis.