Grundlagen Neuronaler Netze: Backpropagation-Algorithmus

Geoffrey Hinton

Geoffrey Hinton ist ein in Großbritannien geborener kanadischer Informatiker und Psychologe, der viele Beiträge zum Bereich der neuronalen Netzwerke geleistet hat. Er ist einer der Erfinder des Backpropagation-Algorithmus und ein aktiver Förderer des Deep Learning. Er gilt als Vater der neuronalen Netzwerke und des Deep Learning.

Darüber hinaus ist Hinton Gründer des Gatsby Centre for Computational Neuroscience an der University of London und derzeit Professor am Department of Computer Science der University of Toronto, Kanada. Seine Hauptforschungsinteressen liegen in der Anwendung künstlicher neuronaler Netzwerke im maschinellen Lernen, Gedächtnis, der Wahrnehmung und der Symbolverarbeitung. Derzeit erforscht Hinton, wie neuronale Netzwerke auf unüberwachte Lernalgorithmen angewendet werden können.

Unter Hintons zahlreichen wissenschaftlichen Forschungsergebnissen ist die Backpropagation jedoch die bekannteste und bildet die Grundlage der meisten aktuellen Algorithmen für überwachtes Lernen neuronaler Netzwerke, die auf der Methode des Gradientenabstiegs basieren. Sein Hauptarbeitsprinzip ist:

Im tatsächlichen Betrieb wird der ANN-Algorithmus im Allgemeinen in drei Kategorien unterteilt: Eingabeschicht, verborgene Schicht und Ausgabeschicht. Wenn zwischen dem Ausgabeergebnis des Algorithmus und dem Zielergebnis ein Fehler auftritt, berechnet der Algorithmus den Fehlerwert und gibt den Fehlerwert dann durch Rückausbreitung an die verborgene Schicht zurück, passt ihn durch Ändern relevanter Parameter an und wiederholt diesen Schritt, bis das erwartete Ergebnis erzielt wird.

Durch Backpropagation kann der ANN-Algorithmus Ergebnisse erzielen, die näher am Ziel liegen. Bevor man jedoch versteht, wie Backpropagation auf den ANN-Algorithmus angewendet wird, muss man zunächst das Funktionsprinzip von ANN verstehen.

KNN ist ein mathematisches Modell oder Computermodell, das auf dem neuronalen Netzwerk des menschlichen Gehirns basiert und aus einer großen Anzahl miteinander verbundener Knoten (die als biologische Neuronen verstanden werden können) besteht.

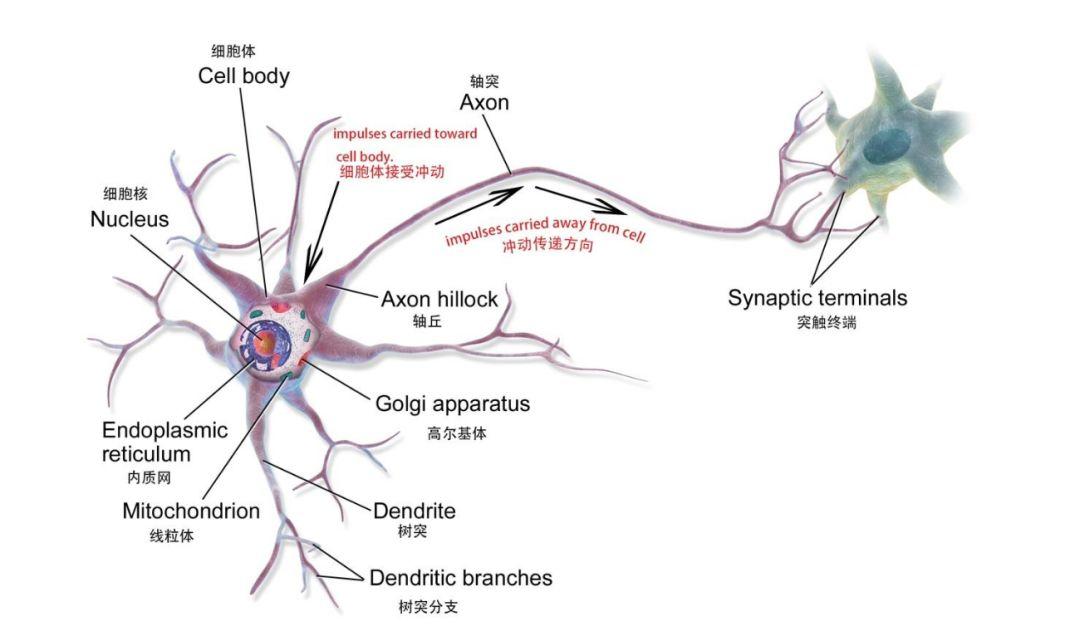
Biologische Neuronen

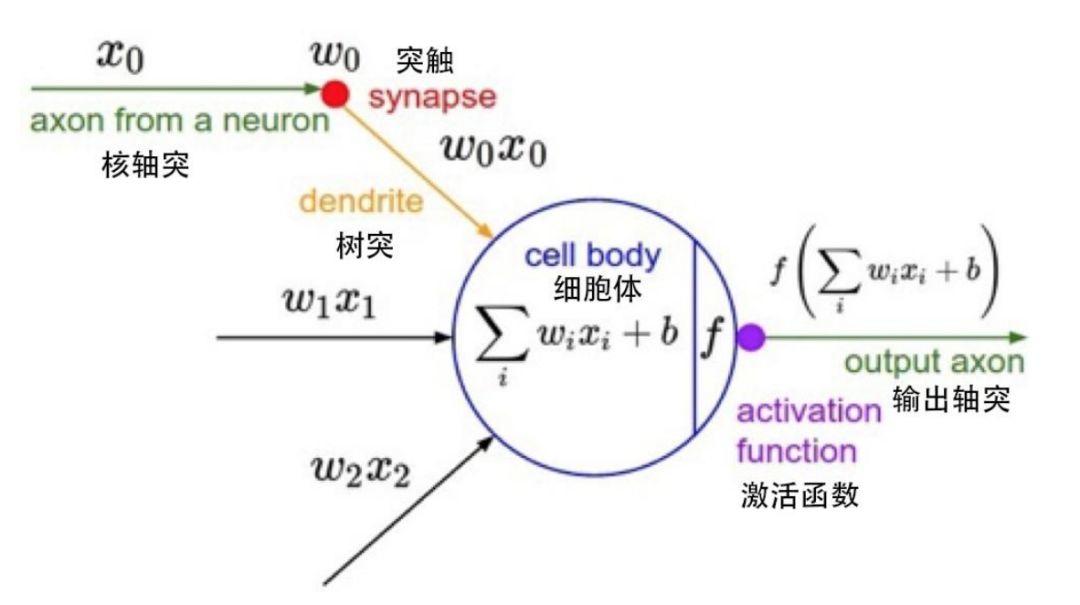
Ein einzelner Knoten in einem mathematischen Modell

Jeder Knoten stellt eine bestimmte Ausgabefunktion dar, die als Aktivierungsfunktion bezeichnet wird. die Verbindung zwischen zwei Knoten stellt einen gewichteten Wert dar, auch Gewichtswert genannt. Während des Betriebs des ANN-Algorithmus entspricht jede Verbindung einem Gewicht w und einem Offset b (auch als ANN-Parameter bezeichnet). Der Ausgabewert bezieht sich auf den Knoten, den Gewichtswert und den Offset.

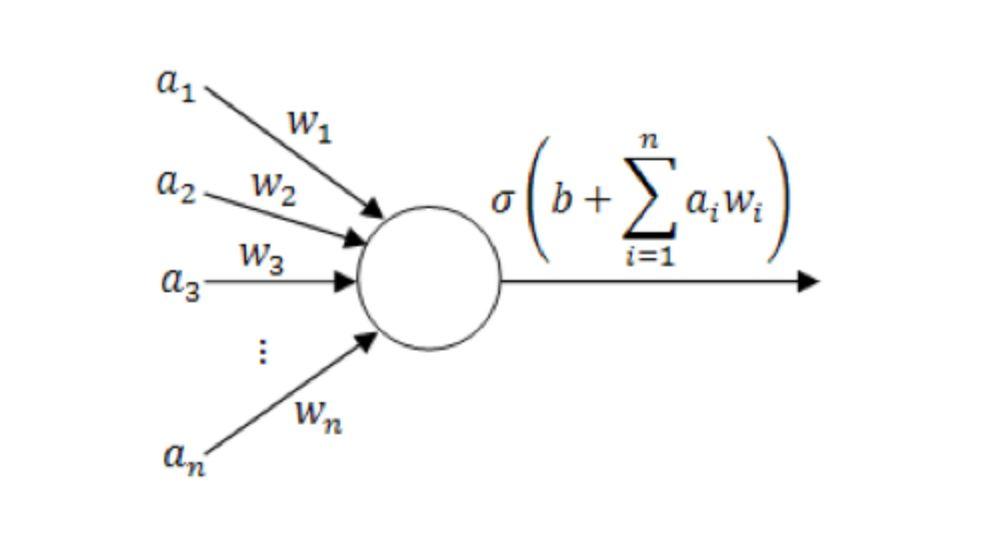
Diagramm eines einzelnen Neuronenmodells

(wo ein1~aN sind die Komponenten des Eingabevektors; w1~wN ist der Gewichtswert; b ist der Versatz; σ ist die Aktivierungsfunktion, wie z. B. tanh, Sigmoid, ReLU usw.)

Ein vollständiges neuronales Netzwerk (KNN) besteht im Allgemeinen aus einer Eingabeschicht, mehreren verborgenen Schichten und einer Ausgabeschicht. Die verborgene Schicht besteht hauptsächlich aus Neuronen und übernimmt die wichtigste Rechenarbeit. Während der eigentlichen Operation treffen die Neuronen in jeder Schicht Entscheidungen und übertragen die Entscheidungen an die Neuronen in der nächsten verborgenen Schicht, bis das Endergebnis ausgegeben wird.

Je mehr verborgene Schichten vorhanden sind, desto komplexer ist das neuronale Netzwerk und desto genauer sind die Ergebnisse. Wenn Sie beispielsweise mithilfe eines neuronalen Netzwerks (KNN) feststellen möchten, ob das eingegebene Tier „eine Katze“ oder „keine Katze“ ist, treffen die Neuronen in jeder verborgenen Schicht nach der Eingabe des Tieres eine Beurteilung, erhalten ein Ergebnis und übertragen das Ergebnis nach unten, bis die letzte Neuronenschicht das Ergebnis ausgibt.

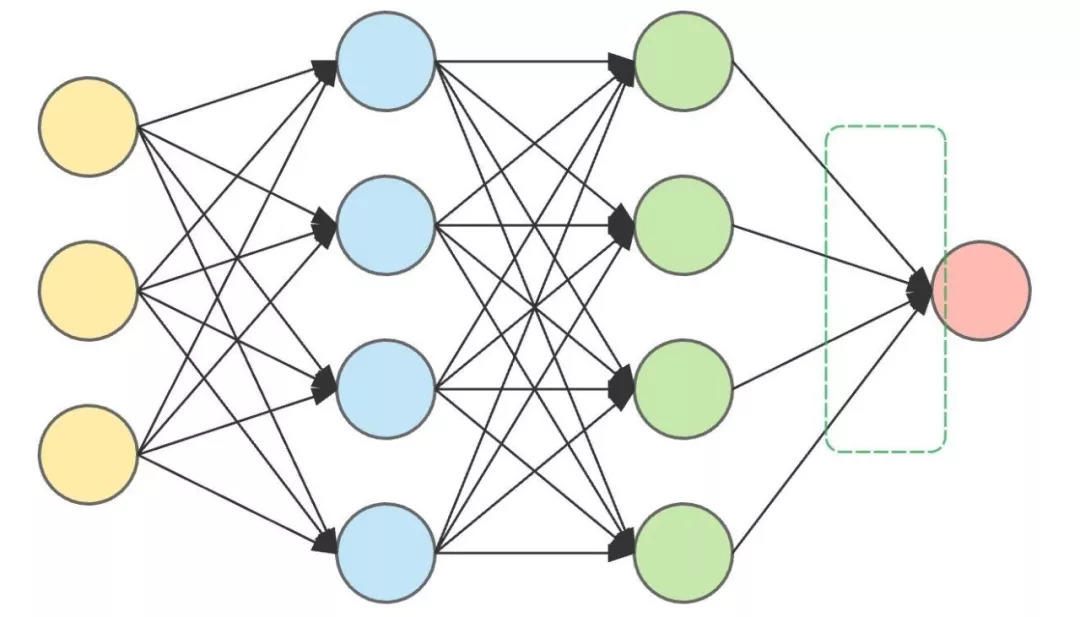
Dies ist eine ANN-Architektur mit zwei verborgenen Schichten.

Die Eingabeebene (links) und die Ausgabeebene (rechts) befinden sich auf beiden Seiten und die beiden verborgenen Ebenen befinden sich in der Mitte.

Wenn das Tier biologisch gesehen eine Katze ist, das ANN aber sagt, dass es „keine Katze“ ist, dann ist die ANN-Ausgabe falsch. Jetzt können wir nur noch zur verborgenen Ebene zurückkehren und die Gewichte und Verzerrungen anpassen. Dieser Vorgang des Zurückgehens und Anpassens der Daten wird als Backpropagation bezeichnet.

Um jedoch eine Rückausbreitung zu erreichen, müssen wir uns auch auf einen wichtigen Algorithmustyp verlassen – den Gradientenabstiegsalgorithmus. Der Gradientenabstieg beschleunigt den Lernprozess erheblich. Vereinfacht lässt sich das so verstehen: Beim Abstieg vom Gipfel ist es am schnellsten, den Weg mit der steilsten Steigung zu wählen.

Da wir zur Änderung der Parameter ständig die Abweichung zwischen der Ausgabe und dem tatsächlichen Wert berechnen müssen (je größer die Differenz, desto größer die Änderung), müssen wir eine Fehlerfunktion (auch Verlustfunktion genannt) verwenden, um den Fehler zwischen dem endgültigen vorhergesagten Wert und dem tatsächlichen Wert aller Stichproben im Trainingssatz zu messen.

In y^i ist das Vorhersageergebnis, yich Für tatsächliche Ergebnisse.

Dieser Ausdruck misst den Fehler zwischen dem endgültigen vorhergesagten Wert und dem tatsächlichen Wert aller Stichproben im Trainingssatz, der sich nur auf die vorhergesagte Kategorie der Ausgabeebene bezieht, dieser vorhergesagte Wert hängt jedoch von den Parametern in den vorherigen Ebenen ab. Wenn wir Hunde nicht als Katzen klassifizieren möchten, müssen wir diese Fehlerfunktion minimieren.

Der Gradientenabstiegsalgorithmus ist einer der Algorithmen, die die Fehlerfunktion minimieren. Es handelt sich außerdem um einen häufig verwendeten Optimierungsalgorithmus beim Training von ANN-Modellen. Die meisten Deep-Learning-Modelle verwenden den Gradientenabstiegsalgorithmus für das Optimierungstraining. Bei einem gegebenen Satz von Funktionsparametern beginnt der Gradientenabstieg mit einem anfänglichen Satz von Parameterwerten und bewegt sich iterativ in Richtung eines Satzes von Parameterwerten, der die Verlustfunktion minimiert. Diese iterative Minimierung wird mithilfe der Infinitesimalrechnung implementiert, wobei Gradientenänderungen in negativer Richtung des Gradienten vorgenommen werden. Das klassische Beispiel für die Verwendung des Gradientenabstiegs ist die lineare Regression. Während das Modell iteriert, konvergiert die Verlustfunktion allmählich zum Minimalwert.

Da der Gradient die Richtung der maximalen Änderungsrate einer Funktion an einem bestimmten Punkt ausdrückt und durch Berechnung der partiellen Ableitung ermittelt wird, wird der Lernprozess durch die Verwendung der Gradientenabstiegsmethode erheblich beschleunigt.

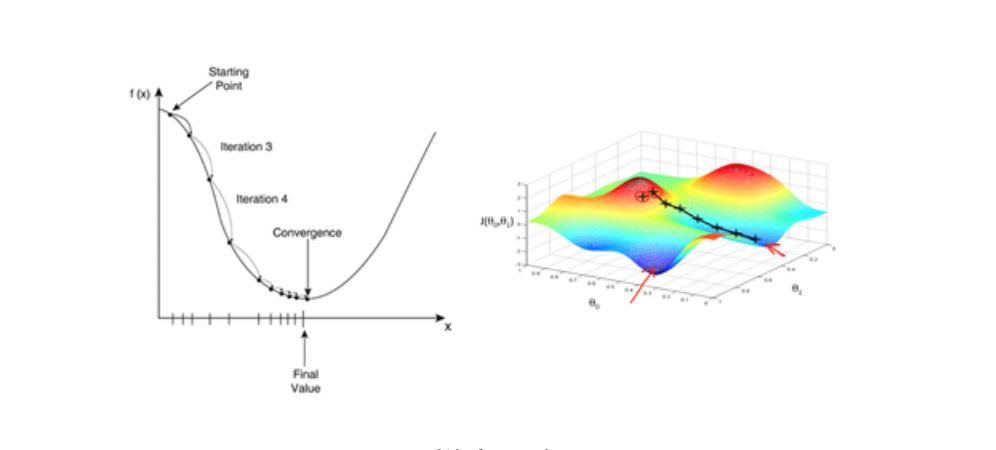
Gradientenabstieg

In der Praxis ist es theoretisch sinnvoll, zunächst zu prüfen, wie sich die Gewichtswerte und Bias in der letzten Schicht auf das Ergebnis auswirken. Indem wir die partielle Ableitung der Fehlerfunktion E bilden, können wir den Einfluss von Gewichtungswerten und Offsets auf die Fehlerfunktion erkennen.

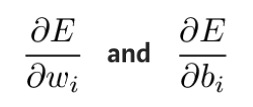
Diese partiellen Ableitungen können mithilfe der Kettenregel berechnet werden, um herauszufinden, wie sich Änderungen dieser Parameter auf die Ausgabe auswirken. Die Herleitungsformel lautet wie folgt:

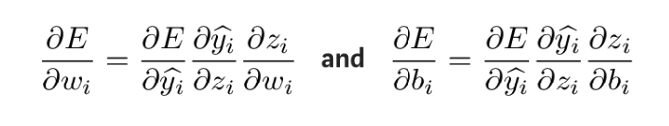
Um die unbekannte Größe im obigen Ausdruck zu erhalten, nehmen Sie die partielle Ableitung von zi in Bezug auf wi bzw. bi:

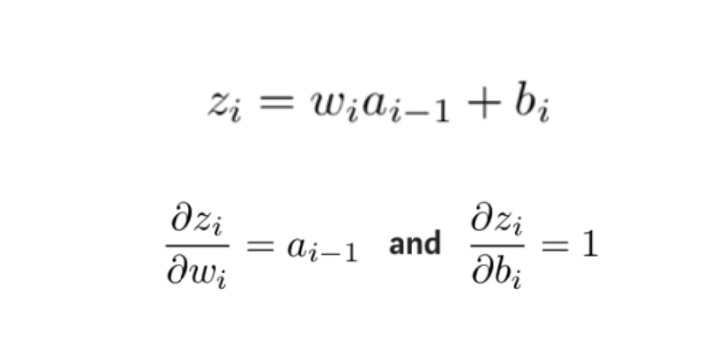Anschließend werden die partiellen Ableitungen der Fehlerfunktion in Bezug auf die Gewichte und Offsets jeder Schicht in umgekehrter Reihenfolge berechnet und die angepassten Gewichte und Offsets mit der Gradientenabstiegsmethode bis zur ersten Schicht aktualisiert, in der der Fehler auftritt.

Bei diesem Prozess handelt es sich um den Backpropagation-Algorithmus, auch als BP-Algorithmus bekannt, der den Fehler der Ausgabeschicht Schicht für Schicht rückwärts propagiert und die Netzwerkparameter durch Berechnung partieller Ableitungen aktualisiert, um die Fehlerfunktion zu minimieren, sodass der ANN-Algorithmus die erwartete Ausgabe erhalten kann.

Derzeit wird Backpropagation hauptsächlich in ANN-Algorithmen unter überwachtem Lernen verwendet.