Der Neue KI-Ansatz Von Google DeepMind Für Den Millennium-Preis Zielt Darauf Ab, Neue Instabile Singularitäten in Drei Flüssigkeitsgleichungen Zu entdecken.

Bereits Ende Mai dieses Jahres gab der Mathematiker Javier Gómez Serrano in einem Interview bekannt, dass er mit Google DeepMind zusammenarbeitet, um„Der Versuch, eines der schwierigsten Rätsel der Menschheit – die Navier-Stokes-Gleichungen – so schnell wie möglich zu lösen.“Die Gleichung ist eines von sieben Millennium-Problemen, die vom Clay Mathematics Institute verliehen werden. Für den Löser ist ein Preisgeld von 1 Million US-Dollar vorgesehen.

Es wird berichtet, dass das von Javier Gómez Serrano und anderen initiierte Projekt „Operation Navier-Stokes“ drei Jahre lang andauert und von einem 20-köpfigen Team durchgeführt wird. Es wurde stets streng vertraulich behandelt. Demis Hassabis, Leiter von Google DeepMind, gab jedoch in einem Interview im Januar dieses Jahres bekannt, dassEr sagte, er stehe kurz davor, ein Millennium-Preis-Problem zu lösen, nannte aber nicht, um welches es sich handele. „Wir werden die Antwort innerhalb des nächsten oder eineinhalb Jahres wissen.“

Nun scheint diese mysteriöse Operation nach und nach aufgedeckt worden zu sein.

Google DeepMind hat in Zusammenarbeit mit Forschern der New York University, der Stanford University, der Brown University und anderen Institutionen ein Framework für maschinelles Lernen und einen hochpräzisen Gauss-Newton-Optimierer entwickelt.In drei verschiedenen Flüssigkeitsgleichungen wurden erstmals systematisch neue instabile Singularitäten entdeckt.Es wird eine prägnante empirische asymptotische Formel offenbart, die die Explosionsrate mit der Instabilitätsordnung verknüpft.

Die experimentellen Ergebnisse zeigen, dassDie Methode erreichte bei allen gefundenen Lösungen eine deutlich bessere Genauigkeit als bestehende Arbeiten.Bei bestimmten CCF-Lösungen liegen die Ergebnisse sogar nahe an der Maschinengrenze für Gleitkommazahlen mit doppelter Genauigkeit und werden nur durch den Rundungsfehler der GPU-Hardware begrenzt. Dies bietet ein neues Forschungsparadigma für die Erforschung der komplexen Landschaft nichtlinearer partieller Differentialgleichungen (PDEs) und eröffnet neue Wege zur Überwindung langjähriger Probleme in der mathematischen Physik.

Die zugehörige Forschung trägt den Titel „Discovery of Unstable Singularities“ und wurde als Vorabdruck auf arXiv veröffentlicht.

Papieradresse:
https://go.hyper.ai/iGh6t
Folgen Sie dem offiziellen Konto und antworten Sie mit „Unstable Singularity“, um das vollständige Dokument herunterzuladen

Entdecken und analysieren Sie zweistufige Strukturen und finden Sie instabile Singularitäten

Blickt man auf die Geschichte der menschlichen Erforschung der Naturgesetze zurück, so war die Strömungsmechanik schon immer eines der komplexesten und anspruchsvollsten Gebiete. Jahrhundertelang stützten sich Mathematiker auf komplexe Gleichungen, um die physikalischen Gesetze von Hurrikanwirbeln bis hin zum Auftrieb von Flugzeugflügeln zu beschreiben. Ob sich in Flüssigkeiten Singularitäten oder Explosionen bilden, bleibt jedoch eines der grundlegendsten und ungelöstesten Probleme der Mathematik. Dieses Phänomen bezieht sich aufWenn die Lösung der maßgebenden Gleichungen (wie etwa der dreidimensionalen Eulergleichungen) von glatten Anfangsbedingungen ausgeht, können sich unendliche Gradienten entwickeln.

Traditionelle numerische Methoden identifizieren hauptsächlich stabile Singularitäten. Dabei handelt es sich um robuste Ergebnisse, die selbst bei geringfügigen Störungen der Anfangsbedingungen entstehen können. Instabile Singularitäten sind dagegen äußerst schwierig zu erfassen, da sie eine unendlich genaue Anpassung der Anfangsbedingungen erfordern.Denn in diesem höchst instabilen Zustand führt selbst eine kleine Störung sofort dazu, dass die Lösung von der Explosionsbahn abweicht.Bei einigen wichtigen ungelösten Problemen – etwa bei grenzenfreien Euler- und Navier-Stokes-Fällen – gibt es in der mathematischen Gemeinschaft jedoch weit verbreitete Spekulationen, dass instabile Singularitäten eine entscheidende Rolle spielen könnten.

Als Antwort auf dieses seit Jahrhunderten ungelöste ProblemDie Forscher durchliefen zwei Phasen: Lösungsfindung und Lösungsanalyse.Erreichen Sie eine hochpräzise Entdeckung instabiler Singularitäten.

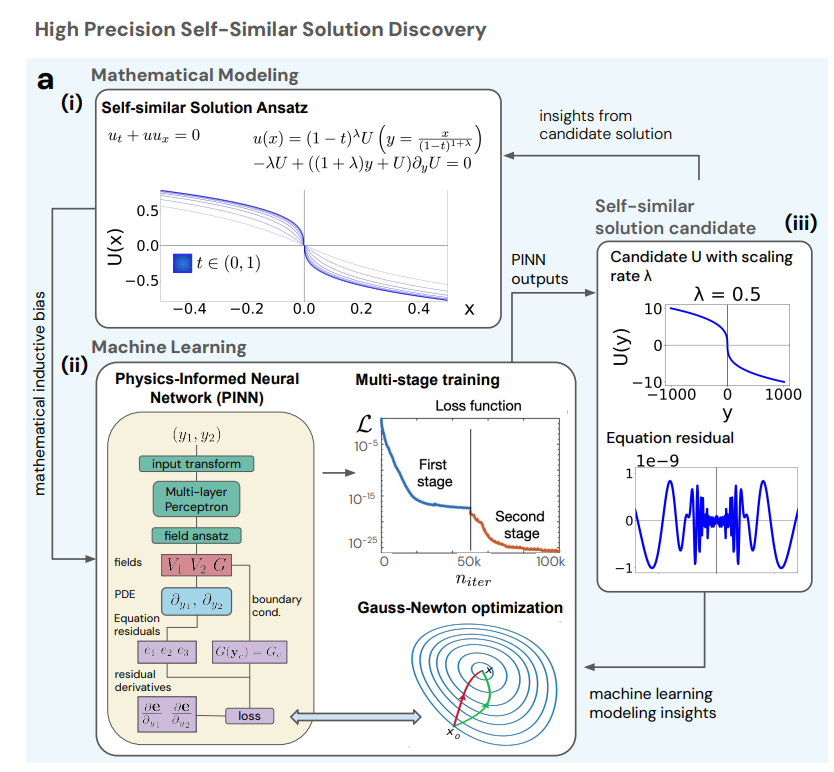
Erste,Die Forscher nutzten eine Kandidatenlösung, um nach explosiven Lösungen mit einem selbstähnlichen Skalierungsfaktor λ und ihrer selbstähnlichen räumlichen Verteilung für die Burgers-Gleichung zu suchen, wie in Abbildung (i) unten dargestellt. Anschließend nutzten sie einen iterativen Ansatz, um den maschinellen Lernprozess und die Genauigkeit der Lösung kontinuierlich zu optimieren (siehe Abbildung ii unten). Die empirischen Ergebnisse und die Genauigkeit der Kandidatenlösung dienten als Grundlage für die mathematische Modellierung und den Entwurf der neuronalen Netzwerkarchitektur, die wiederum die induktiven Verzerrungen in der Netzwerkarchitektur beeinflussten, wie z. B. die Transformation der Eingangskoordinaten und die morphologische Gestaltung des Ausgabefelds.

In diesem Prozess verwendeten die Forscher ein physikalisches Informationsneuronales Netzwerk (PINN), kombiniert mit einem Gauss-Newton-Optimierer und einer mehrstufigen Trainingsstrategie, um hochpräzise Kandidatenlösungen zu generieren und gleichzeitig die richtige Skalierungsrate λ zu finden.

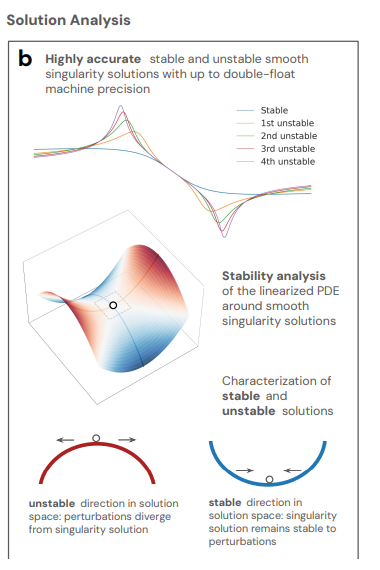
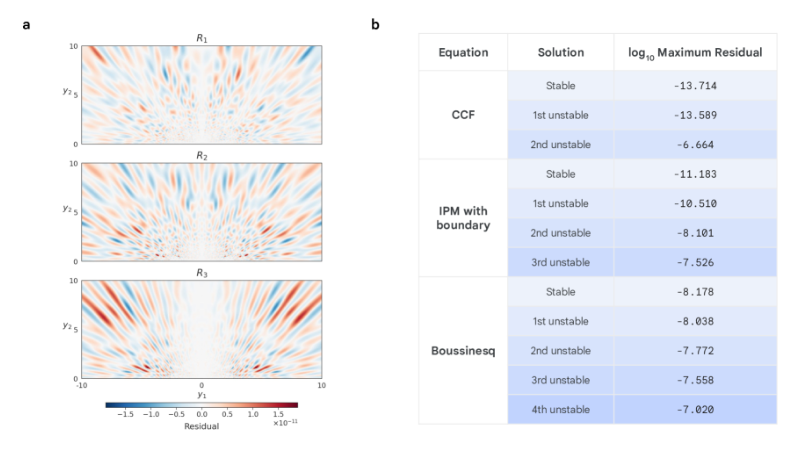
Zweitens,Bei der Analyse der Lösungen analysierten die Forscher für jede instabile Lösung der CCF-, IPM- und Boussinesq-Gleichungen deren Stabilität, indem sie die umgebenden partiellen Differentialgleichungen linearisierten. Für jede n-te instabile Lösung fanden die Forscher n instabile Modi, die dieselben Symmetrieannahmen wie die Lösung aufweisen.

Diese instabilen Modi zeigen Richtungen auf, in denen die Lösung zu größerer Stabilität geführt werden kann. Sie zeigen, dass die Familie der gefundenen Lösungen innerhalb des Bereichs der betrachteten zulässigen λ-Werte vollständig ist. Dies ermöglicht es den Forschern, nicht nur den Stabilitätsgrad, sondern auch die Entdeckung stabiler und instabiler Singularitäten mit hoher Präzision zu charakterisieren.

Mathematische Erkenntnisse + neuronale Netzwerke machen PINN zu einer neuen Waffe

In dieser Studie erhielten neuronale Netzwerke für physikalische Informationen neue Möglichkeiten, die über ihre typische Rolle als allgemeines Werkzeug zur Lösung partieller Differentialgleichungen hinausgingen. Das Forschungsteam stellte die Lösung als glatte Funktion dar, die durch das neuronale Netzwerk parametrisiert wurde.Ermöglicht die direkte Einbettung mathematischer Erkenntnisse in neuronale Netzwerkarchitekturen und lenkt den Optimierungsprozess in Richtung mathematisch relevanter Lösungen.

Das Forschungsteam nutzte Architekturdesign, um aus den zugrunde liegenden Gleichungen abgeleitete Einschränkungen wie Symmetrie, Periodizität und den Umgang mit unendlichen Domänen durchzusetzen und so einen robusten Standard-Trainingsparameter für das Lernen bereitzustellen. Durch iterative Optimierung der Netzwerkarchitektur mithilfe einer Feedbackschleife aus numerischen Experimenten und mathematischen Analysen berücksichtigten sie dieses Verhalten explizit und schrieben die verbleibenden Gleichungen neu, wodurch die Optimierungsstabilität deutlich verbessert wurde.

Verbessertes hochpräzises Training

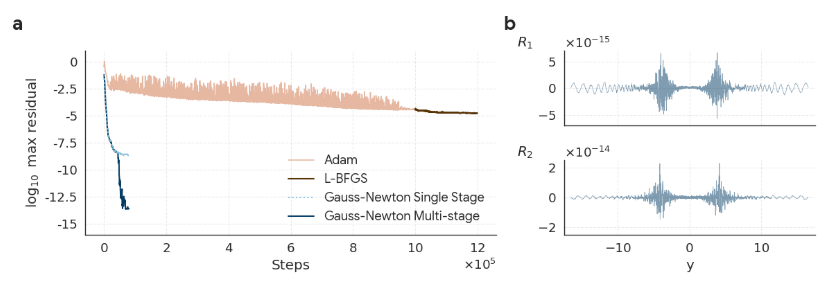
Um die für instabile Singularitäten erforderliche extrem hohe Genauigkeit zu erreichen, nahmen die Forscher zwei wesentliche Verbesserungen am Trainingsprozess vor.Für ein hochpräzises Training werden der Gauss-Newton-Optimierer und das mehrstufige Training eingeführt.

Der Grund für die Einführung dieses Optimierers liegt darin, dass derzeit gängige Standardgradientenoptimierer (wie Adam oder L-BFGS) nicht ausreichen, um qualitativ hochwertige Lösungen für die Gleichung zu erzeugen. Daher wählte das Forschungsteam die leistungsfähigere Gauss-Newton-Optimierungsmethode zur Optimierung des neuronalen Netzwerks. Aufgrund der geringen Größe des Netzwerks war diese zuvor nicht realisierbare Lösung erfolgreich. Experimentelle Ergebnisse zeigen, dass Gauss-Newton den Restfehler in etwa 50.000 Iterationen auf 10⁻⁸ reduzieren kann.Es zeigt eine bessere Leistung und eine deutlich schnellere Konvergenz als der Standardgradientenoptimierer.

Zusamenfassend,Die Idee des mehrstufigen Trainings besteht darin, zunächst ein Netzwerk zu trainieren, um eine ungefähre Lösung zu erhalten, und dann ein zweites Netzwerk zu trainieren, um gezielt die Fehler zu korrigieren, mit denen das vorherige Netzwerk nicht gut umgegangen ist.Durch die Kombination der Ergebnisse der beiden Netzwerke kann die Genauigkeit der Lösung erhöht werden. In Experimenten mit stabilen Lösungen und instabilen Lösungen erster Ordnung der CCF- und IPM-Gleichungen konnte die mehrstufige Trainingsmethode den maximalen Residuenwert um fünf Größenordnungen verbessern – eine Genauigkeit, die ausreicht, um die strenge mathematische Verifizierung auf Basis von CAP zu erfüllen.

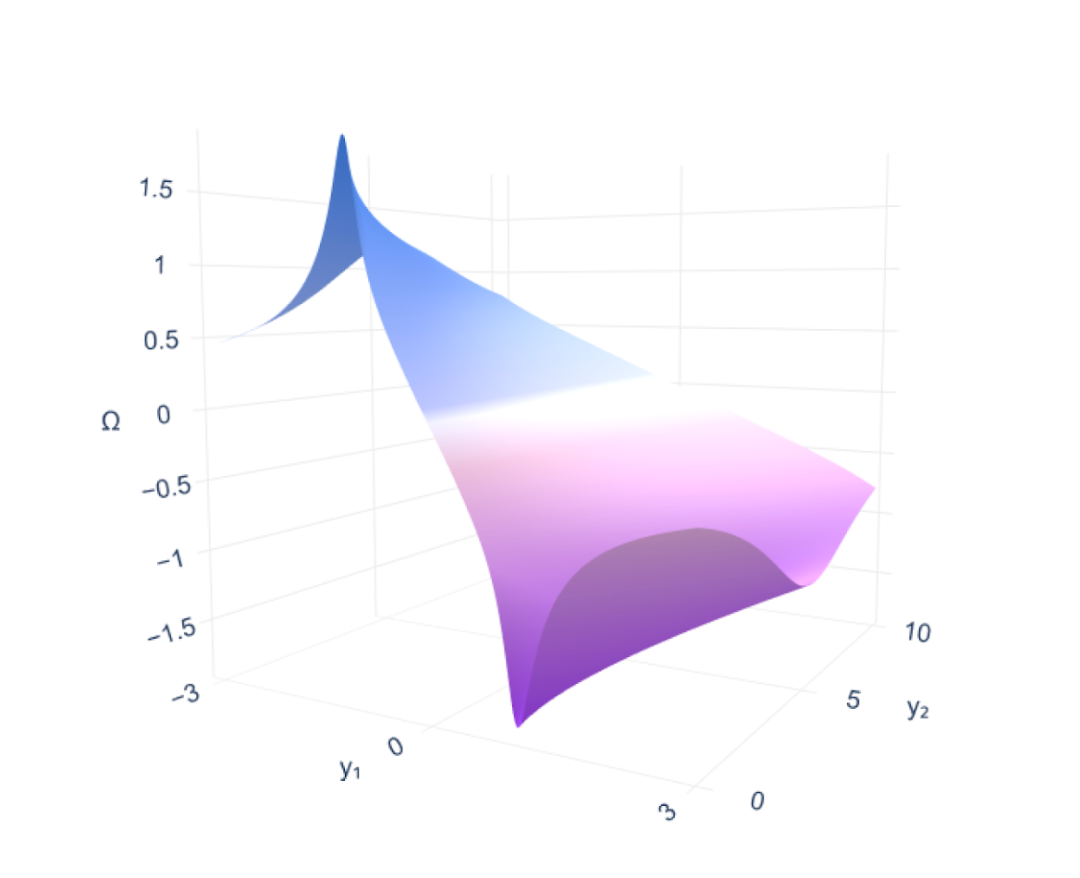
Dieser Ansatz ermöglicht dem Modell eine neue Genauigkeitsstufe. Anhand der dreidimensionalen Visualisierung und Analyse zweidimensionaler Wirbelfelder als Referenzbeispiele demonstrierte das Forschungsteam eine Messung des Rotationsgrades der Flüssigkeit an jedem Punkt. Der maximal behobene Fehler entspricht einer Verbesserung der Vorhersagegenauigkeit des Erddurchmessers auf wenige Zentimeter.

Papier 1 Als chinesischer Ph.D.

Yongji Wang, der Hauptautor des Artikels, ist derzeit Postdoktorand am Courant Institute of Mathematical Sciences der New York University und Gastdozent an der Stanford University. Seine Forschungsinteressen umfassen Kontinuumsmechanik, Geophysik und wissenschaftliches maschinelles Lernen. Er verfügt über umfangreiche Erfahrung in der Anwendung theoretischer und numerischer Techniken zur Aufklärung komplexer physikalischer Prozesse in Natur und Umwelt.

Der Forschungsschwerpunkt liegt auf der Entwicklung hochpräziser Deep-Learning-Techniken für eine Vielzahl wissenschaftlicher Probleme, die von der Aufdeckung verborgener physikalischer Eigenschaften antarktischer Eisschelfe bis hin zur Suche nach selbstähnlichen explosiven Lösungen für nichtlineare partielle Differentialgleichungen (PDEs) reichen.

Quellen:
1.https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/
2.https://english.elpais.com/science-tech/2025-06-24/spanish-mathematician-javier-gomez-serrano-and-google-deepmind-team-up-to-solve-the-navier-stokes-million-dollar-problem.html

3.https://mp.weixin.qq.com/s/CRlGLmji4BWNkNaA7e2JEw