Eine Neue Ära Der Materialforschung! Das Team Von Xu Yong Und Duan Wenhui Von Der Tsinghua-Universität Hat Ein Funktionales Framework Für Die Dichte Neuronaler Netzwerke Veröffentlicht, Um Die Blackbox Der Vorhersage Elektronischer Strukturen Zu Öffnen!

Die Dichtefunktionaltheorie (DFT) spielt als zentrales Werkzeug zur Vorhersage und Erklärung von Materialeigenschaften eine unverzichtbare Rolle in der Physik, Chemie, Materialwissenschaft und anderen Bereichen.Allerdings erfordert die herkömmliche DFT normalerweise viele Rechenressourcen und Zeit und ihr Anwendungsbereich ist erheblich eingeschränkt.

Als aufstrebendes interdisziplinäres Feld überwindet die Kombination von Deep Learning mit der Dichtefunktionaltheorie zur Vorhersage und Entdeckung neuer Materialien durch eine große Anzahl von Computersimulationen allmählich die Mängel traditioneller DFT-Berechnungen, die zeitaufwändig und komplex sind, und bietet ein großes Anwendungspotenzial beim Aufbau computergestützter Materialdatenbanken. Algorithmen neuronaler Netzwerke beschleunigen den Aufbau größerer Materialdatenbanken und größere Datensätze können leistungsfähigere Modelle neuronaler Netzwerke trainieren. Allerdings werden in den meisten aktuellen Deep-Learning-DFT-Forschungen die DFT-Aufgabe und das neuronale Netzwerk getrennt behandelt, was die gemeinsame Entwicklung der beiden stark einschränkt.

Um den neuronalen Netzwerkalgorithmus und den DFT-Algorithmus organischer zu kombinieren, schlug die Forschungsgruppe von Xu Yong und Duan Wenhui von der Tsinghua-Universität das Framework der Dichtefunktionaltheorie neuronaler Netzwerke (neuronales Netzwerk DFT) vor.Dieses Framework vereint die Minimierung von Verlustfunktionen in neuronalen Netzwerken und die Optimierung von Energiefunktionalen in der Dichtefunktionaltheorie. Im Vergleich zu herkömmlichen überwachten Lernmethoden weist es eine höhere Genauigkeit und Effizienz auf und eröffnet einen neuen Weg für die Entwicklung von Deep-Learning-DFT-Methoden.

Die Forschungsergebnisse wurden in Phys veröffentlicht. Ehrw. Lett. unter dem Titel „Dichtefunktionaltheorie neuronaler Netzwerke basierend auf variationeller Energieminimierung“.

Forschungshighlights:

* Diese Studie schlug einen theoretischen Rahmen für die Dichtefunktionaltheorie neuronaler Netzwerke vor, der die Variationsdichtefunktionaltheorie mit äquivalenten neuronalen Netzwerken kombiniert

* Diese Studie basiert auf der Sprache Julia und wird mit dem automatischen Differenzierungsframework Zygote kombiniert, um ein Computerprogramm namens AI2DFT von Grund auf zu entwickeln. In AI2DFT kann die automatische Differenzierung (AD) sowohl für variationsbasierte DFT-Berechnungen als auch für das Training neuronaler Netzwerke verwendet werden.

Papieradresse:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.076401

Das Open-Source-Projekt „awesome-ai4s“ vereint mehr als 100 AI4S-Papierinterpretationen und stellt umfangreiche Datensätze und Tools bereit:

https://github.com/hyperai/awesome-ai4s

Deep Learning und DFT-Integration zum unüberwachten Lernen physikalischer Informationen

Kohn-Sham DFT ist die am weitesten verbreitete First-Principles-Berechnungsmethode in der Materialsimulation.Diese Methode vereinfacht das komplexe Problem der Elektronenwechselwirkung, indem sie es in ein vereinfachtes Problem nicht wechselwirkender Elektronen abbildet, das durch einen effektiven Kohn-Sham-Hamiltonoperator für einzelne Teilchen beschrieben wird, und verwendet eine ungefähre Austauschkorrelationsfunktion, um die komplexen Vielteilcheneffekte zu berücksichtigen. Obwohl die Kohn-Sham-Gleichung formal aus dem Variationsprinzip abgeleitet ist und im Bereich der theoretischen Physik sehr beliebt ist, wird sie in DFT-Berechnungen nicht oft verwendet, da iterative Lösungen von Differentialgleichungen effizienter sind.

Mit der weiteren Integration von Deep Learning und DFT hat sich dieses Entwicklungsparadigma jedoch vollständig geändert.

Die Forschung zum Deep Learning (DFT) basiert hauptsächlich auf datengesteuerten überwachten Lerntechniken. Wie in Abbildung a unten gezeigt, generieren herkömmliche datengesteuerte Methoden des überwachten Lernens im Allgemeinen Trainingsdaten, indem sie DFT-SCF-Berechnungen an verschiedenen Materialstrukturen durchführen und dann ein neuronales Netzwerk entwerfen und trainieren, um Daten vorherzusagen, die den DFT-Ergebnissen ähneln. Dabei werden neuronales Netz und DFT getrennt.

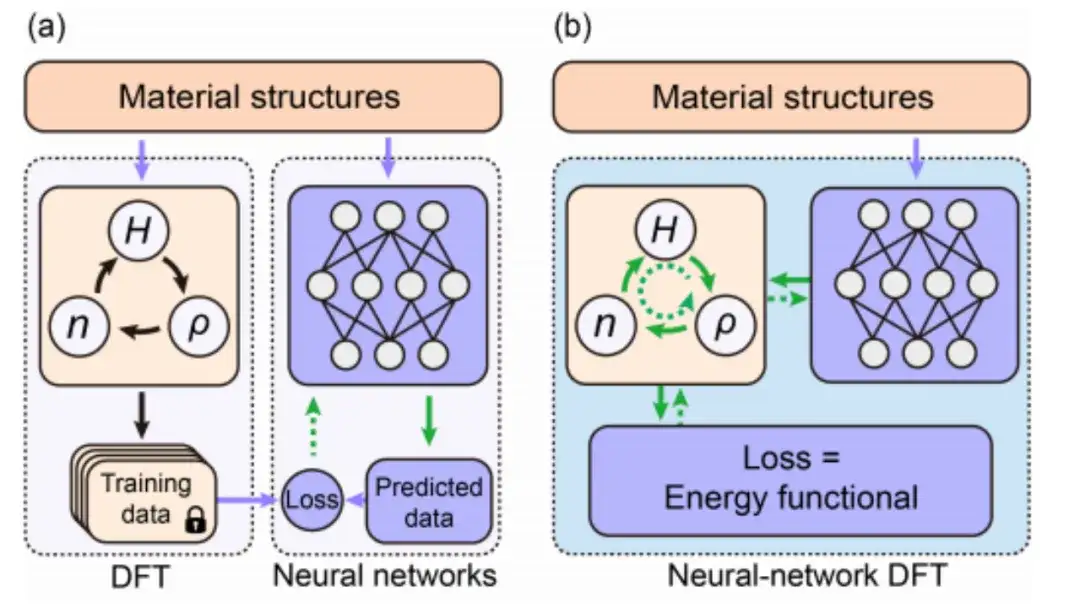
Heutzutage ermöglicht, wie in Abbildung b oben gezeigt, das unüberwachte Lernen physikalischer Informationen auf der Grundlage neuronaler Netzwerk-DFT die gemeinsame Nutzung und Zusammenarbeit von neuronalen Netzwerkalgorithmen und DFT-Algorithmen durch die Kombination der Optimierung der Energiefunktion in DFT mit der Minimierung der Verlustfunktion im neuronalen Netzwerk.Noch wichtiger ist, dass durch die explizite Einführung von DFT in Deep Learning das neuronale Netzwerkmodell die reale physikalische Umgebung besser simulieren kann als frühere Datentrainingsmethoden.

Die Einführung automatischer Differenzierungs- und Backpropagationsverfahren implementiert das neuronale Netzwerk DFT numerisch

In dieser Studie wurde das Energiefunktional E[H] für die Folgestudie ausgewählt und DeepH-E3 übernommen, um die Kovarianz der Abbildung {R} → H in der dreidimensionalen euklidischen Gruppe sicherzustellen.

* DeepH-E3, die DeepH-Architektur der zweiten Generation, die von Xu Yongs Team auf der Grundlage äquivalenter neuronaler Netzwerke entwickelt wurde. Dieses Framework verwendet ein kovariantes neuronales Netzwerk unter einer dreidimensionalen euklidischen Gruppe, um den Hamiltonoperator der Dichtefunktionaltheorie (DFT) vorherzusagen, der der mikroskopischen Atomstruktur entspricht, wodurch die Berechnung der elektronischen Struktur auf der Grundlage erster Prinzipien erheblich beschleunigt wird.

Insbesondere verwendet diese Studie, wie in der folgenden Abbildung gezeigt, die Einbettung von Materialstrukturinformationen als Eingabebedingung des äquivarianten neuronalen Netzwerks und gibt dann die Hamilton-Matrix aus, um das mit Hθ parametrisierte Gewicht des neuronalen Netzwerks zu erhalten. Die Energiefunktion E[H] kann auch als Verlustfunktion E[Hθ] des neuronalen Netzwerks betrachtet werden.

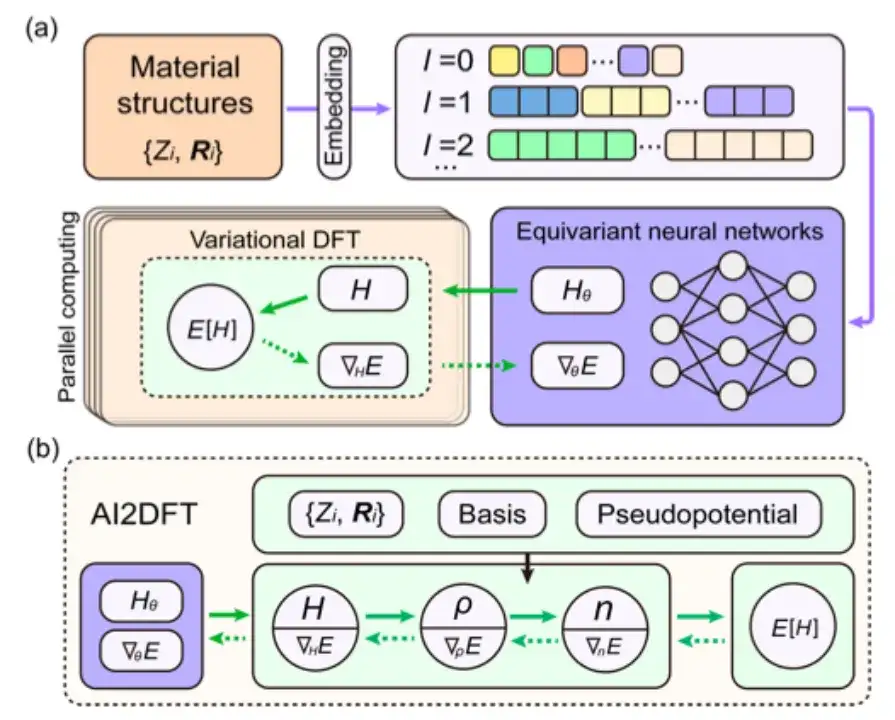
Bei der DFT neuronaler Netzwerke muss das DFT-Programm ∇HE bereitstellen, um die Parameter des neuronalen Netzwerks zu optimieren, was eine große Herausforderung für die DFT-Programmierung darstellt.

Obwohl sich die automatische Differenzierung (AD) gut zur Berechnung von ∇HE eignet, unterstützen die meisten aktuellen DFT-Codes die AD-Funktionalität nicht vollständig. Daher wurde in dieser Studie ein autonomes und nutzbares automatisch differenzierbares DFT-Programm „AI2DFT“ unter Verwendung der Sprache Julia entwickelt. Es ist erwähnenswert, dass in AI2DFT die automatische Differenzierung (AD) sowohl auf die DFT-Berechnung als auch auf das Training neuronaler Netzwerke angewendet wird.

In DFT kann AI2DFT ρ und n aus H ableiten, um die Gesamtenergie zu berechnen, und dann AD im umgekehrten Modus verwenden, um ∇nE, ∇ρE und ∇HE nacheinander basierend auf der Kettenregel zu berechnen. In neuronalen Netzwerken können die Gradienteninformationen ∇θE zur Optimierung neuronaler Netzwerke verwendet werden.

Forschungsergebnisse: Das neuronale Netzwerk DFT weist eine hohe Zuverlässigkeit und hervorragende Leistung bei der Vorhersagegenauigkeit auf

Nach der Erstellung des theoretischen Rahmens der neuronalen Netzwerk-DFT und der Fertigstellung der numerischen Implementierung mit dem differenzierbaren AI2DFT-Code wurden im Rahmen der Studie umfassende Tests an einer Reihe von Materialien durchgeführt, darunter H2O-Moleküle, Graphen, einschichtiges MoS2 und raumzentriertes kubisches Na.

Im Einzelnen wurde in der Studie zunächst geprüft, ob die SCF-Iteration von AI2DFT die Benchmark-Ergebnisse des SIESTA-Codes gut reproduzieren konnte. Anschließend wurde eine variationelle DFT angewendet, um dieselben Materialien zu untersuchen.Wie in den Abbildungen a und b unten gezeigt, kann die Gesamtenergie nach Dutzenden von Variationsschritten unterhalb der μeV-Skala konvergieren, und andere physikalische Größen wie Energiegradient, Hamiltonoperator, Dichtematrix und Ladungsdichte zeigen ebenfalls eine exponentielle Konvergenz, was die Zuverlässigkeit und Robustheit der variationellen DFT bestätigt.

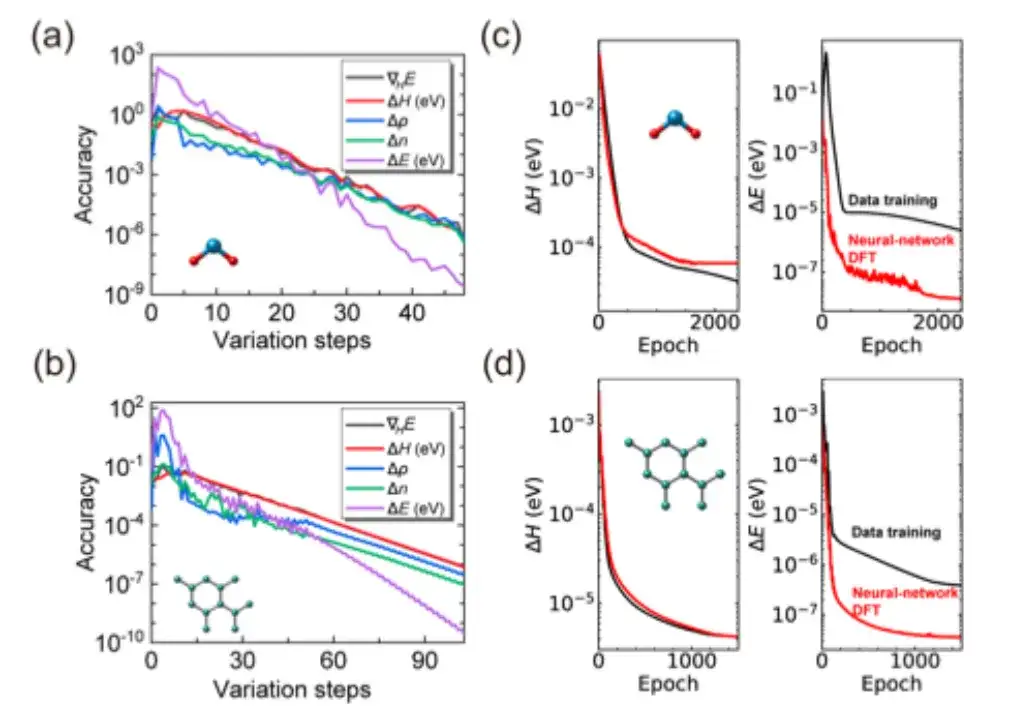
Darüber hinaus kombiniert AI2DFT, wie in den Abbildungen c und d oben gezeigt, im Vergleich zu herkömmlichen datengesteuerten überwachten Lernmethoden die Leistung von variationeller DFT und dem neuronalen Netzwerk DeepH-E3. Zum Beispiel:

* Für das H2O-Molekül kann der DFT-Hamiltonoperator durch neuronales Netzwerk-DFT optimiert werden, um eine hohe Genauigkeit zu erreichen, mit einer Genauigkeit von 0,06 meV für neuronales Netzwerk-DFT und 0,02 meV für das Datentraining.

* Bei Graphen erreichten beide Methoden eine höhere Genauigkeit von 0,004 meV. Damit wurde die Zuverlässigkeit der neuronalen Netzwerkmethode verifiziert.

* Darüber hinaus ist die Leistung des neuronalen Netzwerks DFT im Hinblick auf die Genauigkeit der Energievorhersage deutlich besser als die des Datentrainings. Beispielsweise erreicht die Energievorhersagegenauigkeit des neuronalen Netzwerks DFT für das H2O-Molekül 0,013 μeV, was mehr als 60-mal höher ist als die 0,83 μeV des Datentrainings.

Schließlich wurde in der Studie auch die neuronale Netzwerk-DFT zur Berechnung verschiedener Materialstrukturen angewendet und die Fähigkeit zum unüberwachten Lernen demonstriert.Am Beispiel des H2O-Moleküls (siehe Abbildung a unten) wurde in der Studie zunächst ein vortrainiertes neuronales Netzwerkmodell durch datengesteuertes überwachtes Lernen auf Basis der DeepH-E3-Methode erstellt und anschließend mithilfe der DFT des neuronalen Netzwerks 300 Trainingsstrukturen feinabgestimmt, um hochpräzise Vorhersagen des Hamilton-Operators und anderer physikalischer Größen zu erzielen.

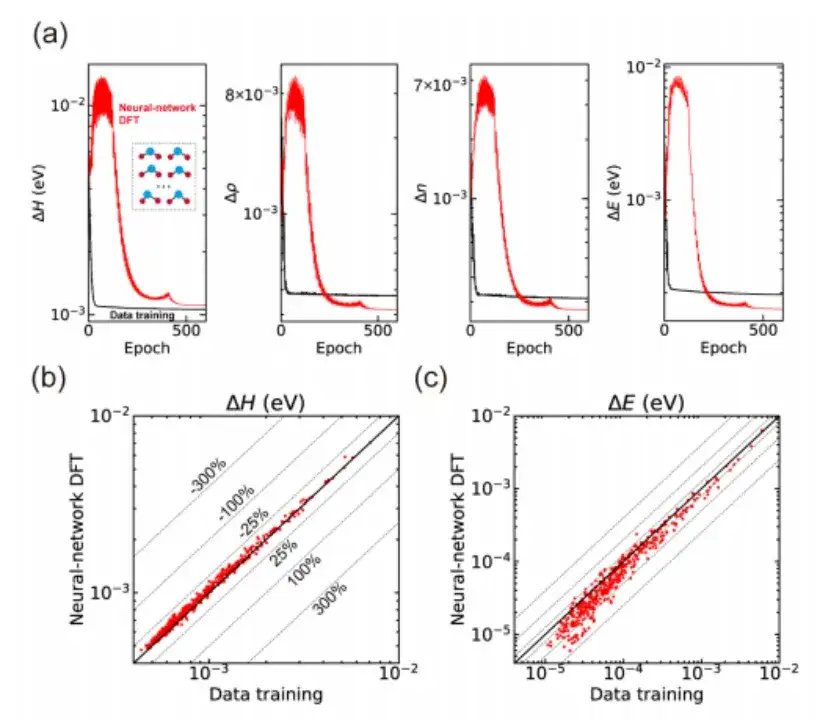
Darüber hinaus wurde in der Studie das trainierte neuronale Netzwerkmodell auch zur Vorhersage von 435 Teststrukturen verwendet, die während des Trainingsprozesses nicht gesehen wurden. Die Ergebnisse zeigten auch eine gute Generalisierungsfähigkeit, wie in den Abbildungen b und c oben gezeigt.Obwohl der durch die neuronale Netzwerk-DFT erzeugte Hamilton-Operator einen etwas größeren mittleren absoluten Fehler im Vergleich zum datengesteuerten überwachten Lernen aufweist, zeigt er hinsichtlich der Vorhersagegenauigkeit eine bessere Leistung, was bedeutet, dass das neuronale Netzwerk durch den neuronalen Netzwerk-DFT-Prozess mehr physikalische Muster lernt.

Mit dem Fokus auf DFT und First-Principles-Berechnungen wird KI eine neue Ära der Materialwissenschaften einleiten

Unter der Leitung von Professor Xu Yong und Professor Duan Wenhui von der Tsinghua-Universität brachte das Forschungsteam Li Yang, Tang Zechen, Chen Zezhou und andere zusammen. Sie haben eine Reihe von Ergebnissen in der Dichtefunktionaltheorie (DFT) und in First-Principles-Berechnungen erzielt. Ihre Arbeit hat die weitverbreitete Anwendung der Deep-Learning-Technologie in der Materialwissenschaft und Physikforschung gefördert.

Seit 2022 hat das Forschungsteam von Xu Yong und Duan Wenhui große Durchbrüche auf dem Gebiet des First-Principles-Computing erzielt.Sie entwickelten ein theoretisches Framework und einen Algorithmus basierend auf Deep Learning – DeepH (Deep DFT Hamiltonian).Diese Methode nutzt das Lokalitätsprinzip elektronischer Eigenschaften voll aus. Es muss lediglich ein mit einem kleinen Systemdatensatz trainiertes Modell verwendet werden, um genaue Vorhersagen für groß angelegte Materialsysteme zu liefern und so die Rechenleistung der elektronischen Struktur nichtmagnetischer Materialien erheblich zu verbessern.

Die entsprechenden Ergebnisse wurden in Nature Computational Science unter dem Titel „Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation“ veröffentlicht.
Link zum Artikel:
https://www.nature.com/articles/s43588-022-00265-6

Um die Abhängigkeit des DFT-Hamiltonoperators magnetischer Materialien von Atomen und magnetischen Strukturen weiter zu untersuchen, schlug das Forschungsteam von Xu Yong und Duan Wenhui im Jahr 2023 die xDeepH-Methode (erweitertes DeepH) vor.Diese Methode verwendet ein tiefes äquivariantes neuronales Netzwerk-Framework, um den DFT-Hamiltonoperator magnetischer Materialien darzustellen und so effiziente Berechnungen der elektronischen Struktur durchzuführen. Diese Errungenschaft stellt nicht nur ein effizientes und genaues Rechenwerkzeug für die Untersuchung magnetischer Strukturen dar, sondern schlägt auch einen gangbaren Weg vor, um Genauigkeit und Effizienz der DFT in Einklang zu bringen.

Die entsprechenden Ergebnisse wurden in Nature Computational Science unter dem Titel „Deep-learning electronic-structure calculation of magnetic superstructures“ veröffentlicht.
Link zum Artikel:
https://www.nature.com/articles/s43588-023-00424-3

Um neuronale Netzwerkmodelle zu entwerfen, die Vorwissen und Symmetrieanforderungen berücksichtigen, schlugen die Forscher außerdem die DeepH-E3-Methode vor.Mit dieser Methode können mithilfe einer kleinen Menge an DFT-Daten kleine Systeme trainiert und anschließend schnell die elektronische Struktur großer Materialsysteme vorhergesagt werden. Dadurch wird nicht nur die Rechengeschwindigkeit um mehrere Größenordnungen verbessert, sondern auch eine hohe Vorhersagegenauigkeit im Submillielektronenvoltbereich erreicht.

Die entsprechenden Ergebnisse wurden in Nature Communications unter dem Titel „General framework for E(3)-equivaant neural network representation of density functional theory Hamiltonian“ veröffentlicht.
Link zum Artikel:
https://www.nature.com/articles/s41467-023-38468-8

Durch die kontinuierliche Optimierung des theoretischen Rahmens hat DeepH eine umfassende Abdeckung von nichtmagnetischen bis hin zu magnetischen Materialien erreicht und zudem erhebliche Verbesserungen bei der Vorhersagegenauigkeit erzielt.In diesem Zusammenhang verwendete das Forschungsteam von Xu Yong und Duan Wenhui außerdem die DeepH-Methode, um ein allgemeines DeepH-Materialmodell zu erstellen.Das Modell kann mit Materialsystemen umgehen, die mehrere Elemente und komplexe atomare Strukturen enthalten, und weist eine hervorragende Genauigkeit bei der Vorhersage von Materialeigenschaften auf.

Die entsprechenden Forschungsergebnisse wurden im Science Bulletin unter dem Titel „Universal materials model of deep-learning density functional theory Hamiltonian“ veröffentlicht.
Link zum Artikel:
https://doi.org/10.1016/j.scib.2024.06.011

Heute hat die Forschungsgruppe von Xu Yong und Duan Wenhui den neuronalen Netzwerkalgorithmus und den DFT-Algorithmus organisch kombiniert und damit einen neuen Weg für die Entwicklung von Deep-Learning-DFT-Methoden eröffnet. Es besteht kein Zweifel daran, dass die KI mit der kontinuierlichen Weiterentwicklung tiefer neuronaler Netzwerkalgorithmen und der Erstellung größerer Datensätze intelligenter wird. Wahrscheinlich werden in naher Zukunft Berechnungen auf der Grundlage grundlegender Prinzipien sowie die Materialfindung und das Design von neuronalen Netzwerken durchgeführt. Dies deutet darauf hin, dass KI die Materialwissenschaft in ein neues datengesteuertes Zeitalter führen wird.