Sagen Sie Die Immobilienpreise in Wuhan Genau Voraus! Das GIS-Labor Der Zhejiang-Universität Schlug Das osp-GNNWR-Modell Vor: Es Beschreibt Komplexe Räumliche Prozesse Und Geografische Phänomene Präzise

Wohnen ist ein wichtiger Bestandteil des menschlichen Wohlbefindens und der sozialen Entwicklung, und die Schwankungen der Immobilienpreise haben in der Gesellschaft große Aufmerksamkeit erregt. China ist ein Land mit einer sehr großen geografischen Ausdehnung. Sogar im selben Zuständigkeitsbereich derselben Stadt werden in unterschiedlichen Gegenden aufgrund unterschiedlicher Wohnumfelder, Schulbezirke, Nebengeschäfte und anderer Faktoren unterschiedliche Immobilienpreise für Häuser erzielt. Daher ist eines der wichtigsten Themen bei der Untersuchung der Immobilienpreise ihre räumliche Differenzierung und der Einflussmechanismus, die sogenannte „räumliche Heterogenität“.

In den letzten Jahren haben räumliche Unterschiede bei den Immobilienpreisen immer größere Bedeutung erlangt und eine einzelne Methode zur Entfernungsmessung reicht nicht aus, um die „räumliche Heterogenität“ der Immobilienpreise in einem komplexen geografischen Umfeld zu erfassen. Insbesondere in Großstädten wie Wuhan haben Faktoren wie natürliche Gegebenheiten (wie Flüsse und Seen) und städtische Infrastruktur (wie Brücken, Tunnel und vielschichtige Straßennetze) einen komplexen Einfluss auf die Immobilienpreise.Herkömmliche geografisch gewichtete Regressionsmodelle (GWR) stehen bei der Messung räumlicher Nähe vor Herausforderungen.

In diesem Zusammenhang veröffentlichten Forscher des GIS-Labors der Zhejiang-Universität ein Forschungspapier mit dem Titel „Ein neuronales Netzwerkmodell zur Optimierung der Messung der räumlichen Nähe im geografisch gewichteten Regressionsansatz: eine Fallstudie zu Hauspreisen in Wuhan“ im International Journal of Geographical Information Science, einer renommierten Zeitschrift auf dem Gebiet der geografischen Informationswissenschaft.

In dieser Studie wurde eine innovative Methode mit neuronalen Netzwerken eingeführt, um eine nichtlineare Kopplung mehrerer räumlicher Näherungsmetriken (wie etwa euklidische Distanz, Reisezeit usw.) zwischen Beobachtungspunkten durchzuführen, um eine optimierte räumliche Näherungsmetrik (OSP) zu erhalten und so die Genauigkeit der Immobilienpreisvorhersage des Modells zu verbessern.

Um das Problem zu lösen, dass abstrakte "räumliche Nähe" keine Verlustfunktionen konstruieren kann und neuronale Netze schwer zu trainieren sind,Diese Studie kombiniert OSP außerdem mit der Methode der geographisch neuronalen gewichteten Regression (GNNWR).Das osp-GNNWR-Modell wurde entwickelt, um das Training des neuronalen Netzwerks durch Lösen der räumlichen nichtstationären Regressionsbeziehung zwischen abhängigen und unabhängigen Variablen zu realisieren.

Forschungshighlights:

• Durch die Einführung einer optimierten räumlichen Nähemetrik und deren Integration in die Architektur des neuronalen Netzwerks wird die Anwendbarkeit der geografisch gewichteten Regression bei der Untersuchung der räumlichen Verteilung geografischer Prozesse wie Immobilienpreise effektiv verbessert.
• Durch die Untersuchung simulierter Datensätze und empirischer Fälle von Immobilienpreisen in Wuhan wird nachgewiesen, dass das in der Arbeit vorgeschlagene Modell insgesamt eine bessere Leistung aufweist und komplexe räumliche Prozesse und geografische Phänomene genauer beschreiben kann.
• Dies eröffnet einen neuen Ansatz für die Untersuchung der Anpassung räumlicher Nähemetriken zur Verbesserung der Leistung verschiedener georäumlicher Regressionsmodelle.

Papieradresse:
https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2343771

Das Open-Source-Projekt „awesome-ai4s“ vereint mehr als 100 AI4S-Papierinterpretationen und stellt außerdem umfangreiche Datensätze und Tools bereit:

https://github.com/hyperai/awesome-ai4s

Datensatz: Wuhan wird als typisches Forschungsgebiet genutzt

Simulierter Datensatz

Um die Anpassungsgenauigkeit des osp-GNNWR-Modells zu bewerten, erstellten die Forscher einen räumlich heterogenen simulierten Datensatz mit 64 × 64 Elementen. Die räumliche Heterogenität des simulierten Datensatzes spiegelt sich nicht nur in der Luftlinienentfernung wider, sondern zeigt auch die durch die nichteuklidische Entfernung definierten räumlichen Verteilungsmerkmale, die die Wirksamkeit von OSP belegen können.

Tatsächlicher Datensatz

Wuhan, die Hauptstadt der Provinz Hubei, liegt in Zentralchina am Zusammenfluss des Han-Flusses und des Jangtse. Wuhan hat ein feuchtes subtropisches Klima mit reichlich Niederschlag und zahlreichen Flüssen, Seen und Teichen, was die Beurteilung der räumlichen Nähe schwierig macht. Als größte und am dichtesten besiedelte Stadt in Zentralchina verfügt Wuhan auch über einen florierenden Immobilienmarkt, der reichlich Daten für die Erstellung eines umfassenden Modells der spezifischen Immobiliendynamik von Wuhan liefert.

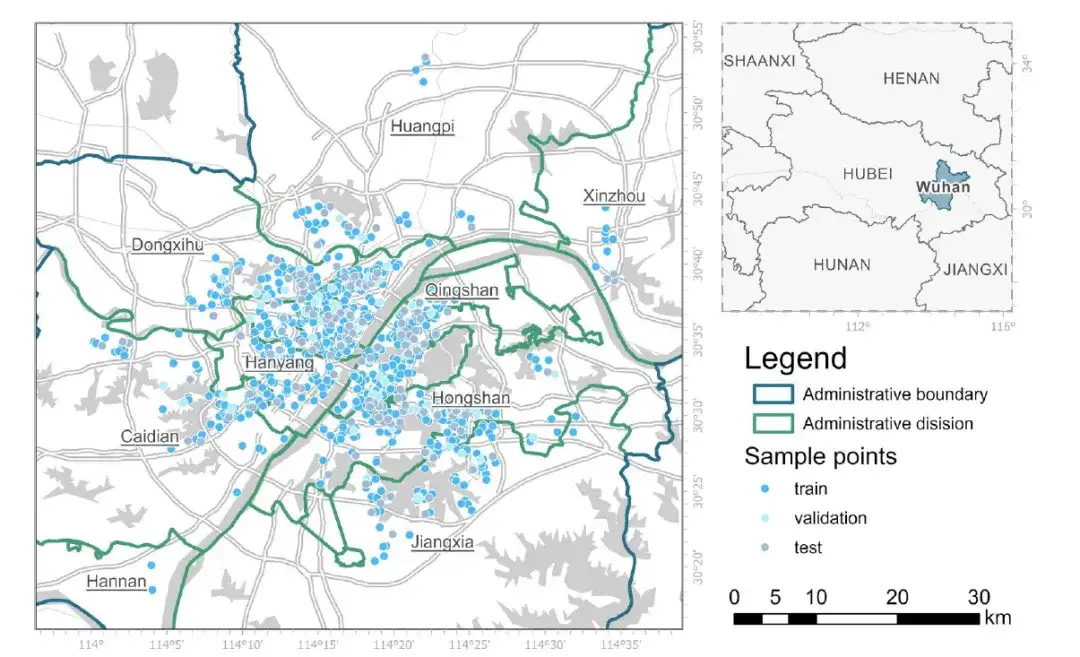
zu diesem Zweck,Die Forscher stellten einen Datensatz mit 968 verschiedenen Immobilienbeispielen zusammen.Diese Daten stammen aus den Aufzeichnungen über Transaktionen mit gebrauchten Wohnungen in Wuhan im Jahr 2019. Die Datenquelle ist Anjuke (https://wuhan.anjuke.com). Alle diese Datensätze wurden bereinigt, spezielle Immobilientypen (wie Villen) wurden ausgeschlossen und die Datenqualität wurde sichergestellt.

Modellarchitektur: Einführung einer optimierten räumlichen Nähemetrik und deren Integration in ein neuronales Netzwerk

Die Konstruktion des osp-GNNWR-Modells gliedert sich in zwei Schritte:

Schritt 1: Ermitteln des optimierten räumlichen Nähemaßes (OSP)

Um eine genauere Messung der räumlichen Nähe bei komplexen geografischen Analysen zu erreichen, wurden in dieser Studie mehrere Entfernungsmessverfahren integriert, darunter die euklidische Distanz, die Manhattan-Distanz und die Reisezeit, um die räumliche Nähe (OSP) zu optimieren. Auf diese Weise kann die optimierte räumliche Nähemessung die verschiedenen Einflussfaktoren in komplexen räumlichen Beziehungen besser widerspiegeln und so die Anpassung und Erklärungskraft des räumlichen Regressionsmodells verbessern.

Schritt 2: Durch die weitere Kombination von OSP mit GNNWR schlugen die Forscher das osp-GNNWR-Modell vor.Wie in der folgenden Abbildung dargestellt:

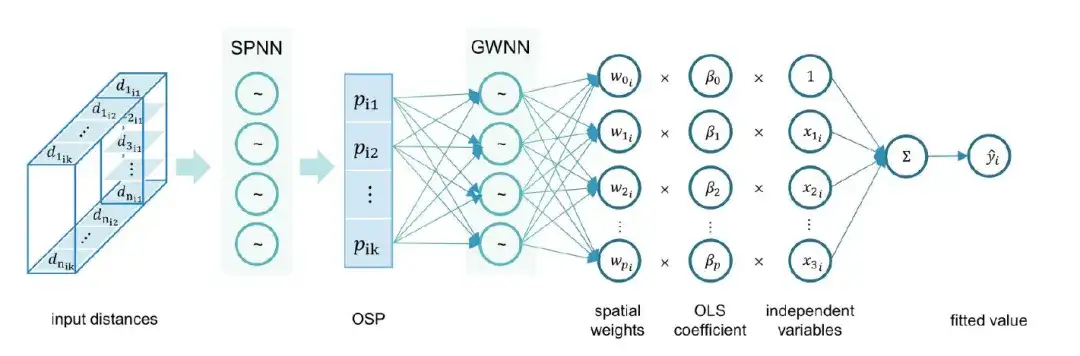
Im Einzelnen sind die Trainings- und Validierungsverfahren des osp-GNNWR-Modells wie folgt:

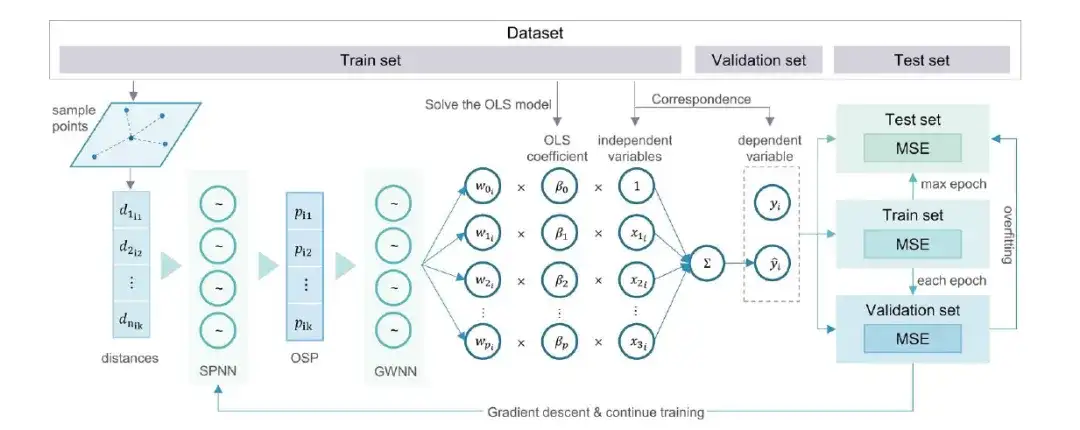
Schritt 1:Extrahieren Sie abhängige und unabhängige Variablen zum Erstellen von Regressionsmodellen.

Schritt 2:Der Datensatz wird zufällig in geeigneten Anteilen in einen Trainingssatz, einen Validierungssatz und einen Testsatz aufgeteilt.

Schritt 3:Stichprobenentfernungen werden als räumliche Informationen im osp-GNNWR-Modell berechnet.

Schritt 4:Mithilfe von Eingabevariablen und räumlichen Informationen wird ein osp-GNNWR-Modell einschließlich Netzwerkstruktur und Hyperparametern erstellt.

Schritt 5:Holen Sie sich Mini-Batch-Daten aus dem Trainingssatz, trainieren Sie mit dem Gradientenabstiegsalgorithmus und bewerten Sie die Anpassungsgüte, z. B. indem Sie den mittleren quadratischen Fehler (MSE) als Verlustfunktion verwenden.

Schritt 6:Bewerten Sie, ob die aktuelle Epoche abgeschlossen ist. wenn nicht, kehren Sie zu Schritt 5 zurück.

Schritt 7:Bewerten Sie die Verlustfunktion des Validierungssatzes, um festzustellen, ob eine Überanpassung vorliegt. wenn der Verlust gegenüber dem vorherigen besten Ergebnis verbessert wird, behalten Sie das neue, bessere Modell bei; andernfalls erhöhen Sie die Anzahl der Überanpassungstoleranzen.

Schritt 8:Bewerten Sie, ob die Überanpassungstoleranz oder die maximale Anzahl von Epochen (max. Epoche) erreicht wurde. Wenn die Grenze erreicht ist, wird das Training beendet und der Testsatz wird verwendet, um das neueste, bessere Modell zu bewerten. Andernfalls fahren Sie mit der Iteration ab Schritt 5 fort.

Durch die oben genannten Schritte können Forscher das osp-GNNWR-Modell effektiv trainieren und validieren, um die Heterogenität in komplexen räumlichen Beziehungen zu erfassen und zu erklären und die Genauigkeit und Zuverlässigkeit des Modells zu verbessern.

Forschungsergebnisse: Das osp-GNNWR-Modell weist eine bessere globale Leistung auf

Schauen wir uns zunächst die Ergebnisse der Analyse anhand des simulierten Datensatzes an. Auf einer Reihe simulierter Datensätze, die auf euklidischer Distanz und Z-Ordnungsdistanz basieren, verwendeten die Forscher zum Vergleich Modelle wie OLS, GWR, GNNWR und osp-GNNWR. Die Ergebnisse sind in der folgenden Tabelle dargestellt:

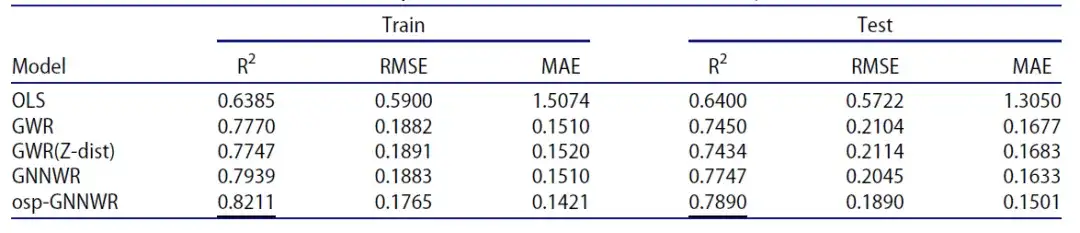
• R²: Ein Maß dafür, wie viel der Variation einer Variablen (der abhängigen Variablen) durch die Variation einer oder mehrerer anderer Variablen (der unabhängigen Variablen) erklärt werden kann. Dieser Wert wird häufig in linearen Regressionsanalysen verwendet, um die Anpassungsgüte des Modells zu beurteilen. 0% bedeutet, dass das Modell keine Variation der Antwortvariablen um ihren Mittelwert erklären kann, d. h., es besteht fast keine Beziehung zwischen dem Modell und den Daten. 100% bedeutet, dass das Modell alle Variationen der Antwortvariablen um ihren Mittelwert erklären kann, d. h., das Modell passt perfekt zu den Daten.
• RMSE (Root Mean Square Error): Wird verwendet, um die Abweichung zwischen dem beobachteten Wert und dem wahren Wert zu messen. Je kleiner der Wert, desto höher ist die Vorhersagegenauigkeit des Modells.
• MSE (mittlerer absoluter Fehler): Wird verwendet, um die durchschnittliche absolute Abweichung zwischen dem vom Modell vorhergesagten Wert und dem tatsächlichen Wert zu messen. Je kleiner der Wert, desto höher ist die Vorhersagegenauigkeit des Modells.

Sowohl im Trainingsdatensatz als auch im Testdatensatz weist das osp-GNNWR-Modell einen höheren R²-Wert, einen niedrigeren RMSE-Wert und einen niedrigeren MSE-Wert auf und zeigt somit eine bessere Leistung. Diese experimentellen Simulationsergebnisse zeigen, dass das im osp-GNNWR-Modell verwendete SPNN-Netzwerk über hervorragende Generalisierungsfähigkeit und einen hochpräzisen Anpassungseffekt bei der Verarbeitung von Eingabedistanzen verfügt. Daher im Vergleich zur traditionellen Methode, die nur auf der euklidischen Distanz beruht,Das osp-GNNWR-Modell bietet potenzielle Vorteile bei der Darstellung der räumlichen Heterogenität realer geografischer Prozesse.

Der zweite Aspekt ist die Leistung des osp-GNNWR-Modells basierend auf den tatsächlichen Immobilienpreisdaten von Wuhan. Die folgende Tabelle zeigt die Ergebnisse des Leistungsvergleichs der Modelle OLS, GWR, GNNWR und osp-GNNWR:

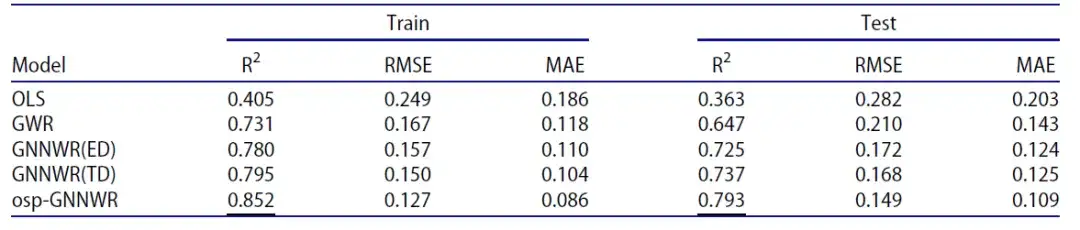
Ebenso weist das osp-GNNWR-Modell sowohl im Trainings- als auch im Testdatensatz einen höheren R²-Wert, einen niedrigeren RMSE-Wert und einen niedrigeren MSE-Wert auf und zeigt somit eine bessere Leistung.

Es ist erwähnenswert, dass das osp-GNNWR-Modell im Vergleich zu GNNWR(TD) den R² des Testdatensatzes von 0,737 auf 0,793 verbessert und den RMSE von 0,168 auf 0,149 und den MAE von 0,125 auf 0,109 reduziert. Diese Ergebnisse zeigen, dassDie Integration von OSP verbessert die Anpassungs- und Vorhersageleistung des osp-GNNWR-Modells.Damit ist es der effektivste Ansatz unter den untersuchten Modellen.

• GNNWR(TD): GNNWR-Modell, das die Reisezeit als Näherungsmaß verwendet.

Insbesondere in Gebieten mit komplexer Naturlandschaft und Infrastruktur, wie dem Westufer des Tangxun-Sees im Bezirk Jiangxia, dem Ufer des Hougong-Sees im Bezirk Caidian und dem Zusammenfluss des Han-Flusses und des Jangtse-Flusses, und in aufstrebenden Entwicklungszonen mit gut ausgebauten Autobahnnetzen und großen Unterschieden zwischen tatsächlicher räumlicher Nähe und physischer Distanz, wie den Bezirken Hongshan und Xinzhou,Der Rest des osp-GNNWR-Modells ist deutlich kleiner als der anderer Modelle, was auf eine höhere Vorhersagegenauigkeit hindeutet.

Insgesamt unterstreichen die Ergebnisse dieser Studie die Wirksamkeit von OSP bei der Verbesserung der Fähigkeit des osp-GNNWR-Modells, räumliche Heterogenität darzustellen, und bringen so die Modellierung komplexer räumlicher Beziehungen innerhalb von Immobilienmärkten voran.

Deep Learning hilft bei komplexen Problemen der Immobilienpreisvorhersage

Die Erforschung der Ursachen und Einflussmechanismen der räumlichen Differenzierung der Immobilienpreise ist von großer Bedeutung, um die stabile Entwicklung des Immobilienmarktes aufrechtzuerhalten und die Stadtplanung und die Wohnzufriedenheit zu verbessern. Allerdings ist die Vorhersage von Immobilienpreisen ein sehr komplexes Thema, bei dem viele Faktoren eine Rolle spielen, wie etwa die geografische Lage, Verkehrsanbindung, Schulbezirk, Alter des Hauses, Haustyp usw. Herkömmliche Methoden basieren oft auf Statistiken und maschinellem Lernen, haben jedoch mit der zunehmenden Größe und Komplexität der Daten nur schwer zurechtzukommen. Deep Learning verfügt über leistungsstarke Funktionen zum Erlernen und Klassifizieren von Merkmalen und kann solche Probleme besser bewältigen.

Um die Genauigkeit der Hauspreisvorhersage zu verbessern, wird die Forschung der Branche hauptsächlich in den folgenden Richtungen durchgeführt:

Einer davon ist der gemischte Modellansatz.Das heißt, Deep Learning und traditionelle Methoden des maschinellen Lernens werden kombiniert, um ihre jeweiligen Vorteile voll auszuspielen. Beispielsweise kann Deep Learning mit herkömmlichen Methoden des maschinellen Lernens wie Support Vector Machines (SVM) oder Random Forests kombiniert werden, um ein Hybridmodell zur Vorhersage von Immobilienpreisen zu erstellen.

Die zweite besteht darin, Zeitreihendaten zu berücksichtigen.Das heißt, bei der Immobilienpreisvorhersage können neben den statischen Eigenschaften des Hauses auch Zeitreihendaten wie historische Immobilienpreise, Wirtschaftsindikatoren usw. berücksichtigt werden. Außerdem können Methoden wie rekurrierende neuronale Netze (RNN) zur Analyse und Vorhersage verwendet werden.

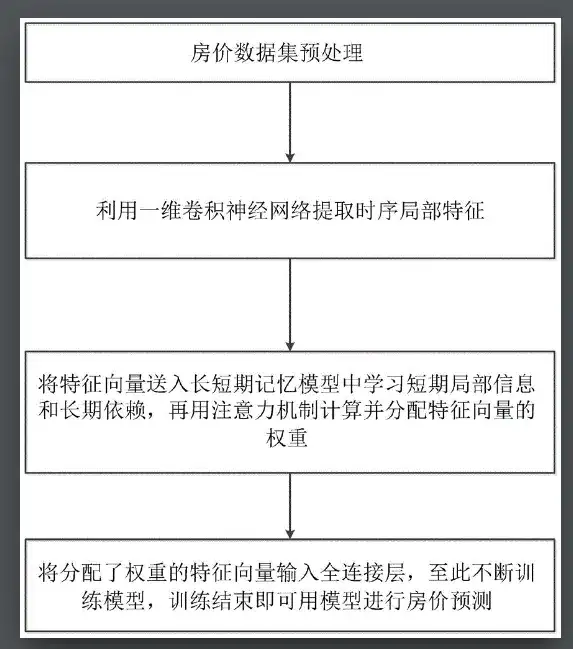
Zum Beispiel,Einige Forscher haben in Google-Patenten eine Methode zur Vorhersage von Immobilienpreisen auf Grundlage von Faltungszeitreihen vorgestellt, die auf einem Aufmerksamkeitsmechanismus basiert.Die Forscher haben zunächst den Datensatz zu den Immobilienpreisen vorverarbeitet und eine Zeitreihe multidimensionaler Faktoren im Zusammenhang mit den Immobilienpreisen erstellt.

Unter Berücksichtigung der mehrdimensionalen Faktoren, die die Immobilienpreise beeinflussen, sowie der Schwankungen und Auswirkungen auf die Immobilienpreisentwicklung wird zur Vorhersage der Immobilienpreise ein auf dem Aufmerksamkeitsmechanismus basierendes Convolutional Time Series Neural Network verwendet. Ein eindimensionales Convolutional Neural Network wird verwendet, um die Merkmale der mehrdimensionalen verwandten Faktoren zu verarbeiten und nach weiterer Merkmalsextraktion und Dimensionsreduzierung einen mehrdimensionalen Merkmalsvektor zu erhalten. Der Merkmalsvektor wird dann in das Langzeit-Kurzzeitgedächtnismodell eingegeben, um den langfristigen Gesamttrend und die kurzfristigen lokalen Abhängigkeitsinformationen zwischen den Merkmalen zu erlernen.

Diese Methode kombiniert den langfristigen Gesamttrend und die kurzfristigen lokalen Informationen der Zeitreihenprognose der Immobilienpreise, reduziert die Varianz der Immobilienpreisprognose und verbessert die Generalisierungsfähigkeit von Methoden zur Immobilienpreisprognose basierend auf mehrdimensionalen Zeitreihendaten.

Der dritte ist die Anwendung von Geographischen Informationssystemen (GIS).Kombinieren Sie Deep Learning mit geografischen Informationssystemen (GIS), um die Auswirkungen von Faktoren wie der geografischen Lage auf die Immobilienpreise zu analysieren und die Vorhersagegenauigkeit des Modells zu verbessern – das oben erwähnte osp-GNNWR-Modell ist ein typisches Beispiel.

Mit der Unterstützung der KI wird das Modell zur Vorhersage von Immobilienpreisen zuverlässiger und genauer. Auf dieser Grundlage können Immobilienunternehmen Investitionsrisiken reduzieren; Die Regierung kann die Informationen zum Wohnungsmarkt umfassend und genau kontrollieren, um eine gezielte Verwaltung durchzuführen, gemeinsam ein gutes Immobilienumfeld zu schaffen und den Menschen dabei zu helfen, wirklich in Frieden und Zufriedenheit zu leben und zu arbeiten.

Quellen:
1.https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2343771
2.https://mp.weixin.qq.com/s/P4nk5sl2v60Q5DeVrOfWLw
3.https://cloud.baidu.com/article/1892933
4.https://patents.google.com/pate