Command Palette
Search for a command to run...
Der Artikel Des Instituts Für Halbleiter Der Chinesischen Akademie Der Wissenschaften Wurde Erneut Im Top-Journal Der TNNLS Veröffentlicht Und Bietet Eine Neue Perspektive Für Die Erforschung Mathematischer Ausdrücke.
Das Lösen mathematischer Ausdrücke ist ein sehr wichtiges Forschungsthema im Bereich des maschinellen Lernens, und die symbolische Regression (SR) ist eine Methode, um aus Daten präzise mathematische Ausdrücke zu finden.
Die symbolische Regression wird verwendet, um den zugrunde liegenden mathematischen Ausdruck gegebener Beobachtungsdaten aufzudecken. Es verfügt über eine natürliche Fähigkeit zur Erklärung und Verallgemeinerung und kann die kausalen Mechanismen zwischen Variablen erklären oder die Entwicklungstrends komplexer Systeme vorhersagen. Es wird auch in verschiedenen Bereichen wie der Physik und Astronomie häufig verwendet.
Ein berühmter Anwendungsfall ist Keplers Entdeckung der Planetenbahnen. Wissenschaftler verwendeten symbolische Regressionsalgorithmen, um einige neue Gesetze der Himmelsbewegung zu entdecken und daraus ihre Umlaufbahnen abzuleiten. Dies ist ein wichtiger Beitrag zur menschlichen Erforschung des riesigen Sternenmeeres im Universum.
Allerdings bringt die symbolische Regressionsforschung auch ihre eigenen Schwierigkeiten mit sich. Bei der symbolischen Regression geht es darum, die beste Kombination dieser Elemente zu ermitteln und die am besten geeigneten Koeffizienten für die unabhängigen Variablen X und die abhängige Variable Y zu finden. Allerdings ist das Ermitteln der besten Kombination ein NP-schweres Problem (nichtdeterministisches Polynom), und der Kombinationsraum wächst exponentiell mit der Länge des symbolischen Ausdrucks. Darüber hinaus stören sich der nichtlineare Lösungsprozess der Koeffizienten und der Optimierungsprozess der Elementkombination gegenseitig, sodass die Ermittlung des genauen Ausdrucks sehr zeitaufwändig ist.
Als Antwort auf dieses akademische ProblemForscher vom Institut für Halbleiter der Chinesischen Akademie der Wissenschaften betrachteten die Lösung der Ausdrucksstruktur als Klassifizierungsproblem und lösten es durch überwachtes Lernen. Sie schlugen ein symbolisches Netzwerk namens DeepSymNet zur Darstellung symbolischer Ausdrücke vor.Im Vergleich zu mehreren gängigen SR-Algorithmen, die auf überwachtem Lernen basieren, verwendet DeepSymNet kürzere Beschriftungen, reduziert den Vorhersagesuchraum und verbessert die Robustheit des Algorithmus.

Papieradresse:
https://ieeexplore.ieee.org/document/10327762
Folgen Sie dem offiziellen Konto und antworten Sie mit „DeepSymNet“, um das Dokument herunterzuladen
Einschränkungen bestehender Methoden hervorgehoben
Es gibt zwei Haupttypen von Lösungen für die derzeit beliebte symbolische Ausdrucksstruktur:
- Suchbasierte Lösungen
Die klassische suchbasierte Lösung ist der GP-Algorithmus (Genetische Programmierung). Zunächst werden viele Ausdrücke zufällig als Ausgangspopulation erhalten, dann wird die Evolution durch Replikation, Austausch und Mutation durchgeführt und Nachkommen mit geringerer Güte werden ausgewählt, um die Evolution fortzusetzen, bis der Ausdruck die Güteanforderung erfüllt.
Darüber hinaus besteht eine wichtige Klasse von Methoden unter den suchbasierten Methoden darin, mithilfe von bestärkendem Lernen nach geeigneten Ausdrucksstrukturen zu suchen, wie etwa dem DSR-Algorithmus, der den Symbolbaum als Sequenz kodiert und zur Lösung die Policy-Gradient-Methode im tiefen bestärkenden Lernen verwendet. Die Idee hinter DSR besteht darin, die Wahrscheinlichkeit zu erhöhen, Ausdrücke mit größeren Belohnungen zu ziehen und dadurch Ausdrücke mit kleineren Fehlern zu erzeugen.
Es gibt auch einen SR-Algorithmus für physikalische Formeln – AIFeynman, der hauptsächlich Vorkenntnisse in der Physik nutzt, um die Ausdrucksstruktur zu beurteilen, wodurch der Ausdruck in kleinere Unterprobleme zerlegt und der Suchraum eingeengt wird; Eine andere Methode, die auf spärlicher Optimierung basiert – EQL – verwendet hauptsächlich den BP-Algorithmus in Kombination mit spärlicher Optimierung, um Parameter zu lernen, wodurch ein spärliches Subnetzwerk im EQL-Netzwerk erhalten und dann die mathematische Ausdrucksstruktur ermittelt wird.
Zusätzlich zu den offensichtlichen Mängeln weist diese Art von Methode den allgemeinen Nachteil auf, dass sie langsam ist, da der Suchraum groß ist und die Lösungserfahrung nicht wiederverwendet werden kann.
- Überwachte lernbasierte Lösungen
Auf überwachtem Lernen basierende Lösungen können die zeitaufwändigen Mängel suchbasierter Lösungen überwinden. Repräsentative Methoden sind SymbolicGPT, NeSymReS und E2E.
* SymbolicGPT kodiert symbolische Ausdrücke in Zeichenfolgen und betrachtet die Lösung der Ausdrucksstruktur als Sprachübersetzungsaufgabe. Das GPT-Modell verwendet im Sprachübersetzungsprozess eine große Anzahl künstlich generierter Beispiele für das überwachte Training.
* NeSymReS kodiert den Symbolbaum als Sequenz mittels Pre-Order-Traversal und trainiert ihn mithilfe von Set Transformer;
* E2E kodiert Ausdrucksstruktur und Koeffizienten in Beschriftungen für das Training und sagt dadurch Ausdrucksstruktur und Koeffizienten gleichzeitig voraus.
Bei diesen Lösungen treten jedoch Probleme mit mehreren gleichwertigen Bezeichnungen und unausgewogenen Trainingsbeispielen auf, die während des Trainingsprozesses leicht zu Mehrdeutigkeiten führen und die Robustheit des Algorithmus beeinträchtigen können.Darüber hinaus weisen sie weitere Mängel auf. Beispielsweise berücksichtigt SymbolicGPT relativ einfache Ausdrücke, da die Anzahl der zum Sampling verwendeten Symbole höchstens vier Ebenen beträgt. E2E kodiert Koeffizienten als Beschriftungen, wodurch die Beschriftungen sehr lang werden und die Vorhersagegenauigkeit usw. beeinträchtigt wird.
Ein neuer Ansatz zur Problemlösung – DeepSymNet
Forscher vom Institut für Halbleiter der Chinesischen Akademie der Wissenschaften schlugen ein neues symbolisches Netzwerk namens DeepSymNet zur Darstellung symbolischer Ausdrücke vor und stellten das Gesamtgerüst von DeepSymNet vor.Die erste Schicht sind die Daten, die mittlere Schicht ist die verborgene Schicht und die letzte Schicht ist die Ausgabeschicht.

Die Knoten der verborgenen Schicht bestehen aus Operationssymbolen, einschließlich +, -, ×, ÷, sin, cos, exp, log, id usw., wobei der ID-Operator derselbe ist wie der ID-Operator in EQL.
Die Anzahl der ID-Operatoren in jeder verborgenen Schicht entspricht der Anzahl der Knoten in der vorherigen Schicht, während die anderen Operatoren in jeder verborgenen Schicht nur einmal vorkommen. Die Operator-ID entspricht eins zu eins dem Knoten der vorherigen Schicht, wodurch jede Schicht alle Informationen der vorherigen Schicht nutzen kann. Die anderen Operatoren sind gewöhnliche Operatoren und vollständig mit der vorherigen Schicht verbunden.
Die Verbindung zwischen dem ID-Operator und der vorherigen Schicht ist fest, und der normale Operator hat keine Verbindung zur vorherigen Schicht oder eine oder zwei Verbindungen, was bedeutet, dass in diesem Netzwerk ein Subnetzwerk einen symbolischen Ausdruck darstellt. Je mehr versteckte Ebenen ein Ausdruck einnimmt, desto höher ist die Komplexität des Ausdrucks. Daher kann die Anzahl der verborgenen Ebenen verwendet werden, um die Komplexität eines Ausdrucks grob zu messen.
Beachten Sie jedoch, dass die Eingabeebene über einen speziellen Knoten „const“ verfügt, der zur Darstellung konstanter Koeffizienten in symbolischen Ausdrücken verwendet wird. Nur mit „const“-Knoten verbundene Kanten haben Gewichte (konstante Koeffizienten), um zu verhindern, dass in symbolischen Ausdrücken genügend konstante Koeffizienten vorkommen.
insgesamt,DeepSymNet ist ein vollständiges Netzwerk, das jeden Ausdruck darstellen kann. Das Lösen von SR ist der Prozess der Suche nach Subnetzen in DeepSymNet.
Zwei Gruppen experimenteller Vergleiche zeigen die Vorteile
Das Forschungsteam führte Tests auf der Grundlage künstlich generierter und öffentlicher Datensätze durch und verglich derzeit gängige Algorithmen.
Adresse zum Herunterladen des Datensatzes:
https://hyper.ai/datasets/29321
Im Experiment hat DeepSymNet höchstens 6 versteckte Schichten und unterstützt höchstens 3 Variablen. Das Forschungsteam generierte für jedes Etikett 20 Proben, die jeweils 20 Datenpunkte enthielten. Das Abtastintervall für konstante Koeffizienten und Variablen beträgt [-2,2]. Die Trainingsstrategie besteht im frühzeitigen Abbruch (d. h., das Training wird abgebrochen, wenn der Verlust im Validierungssatz nicht mehr abnimmt). Unterstützt durch Adam Optimizer.
- Testergebnisse zu künstlich generierten Daten
Die Testergebnisse zeigen:
* Die Schwierigkeit der Vorhersage steigt mit der Anzahl der Vorhersageobjekte und auch die verborgene Ebene (d. h. Komplexität) des Ausdrucks nimmt zu.
* Der Engpass bei der Etikettenvorhersage liegt in der Wahl des Operators.
* DSN2 löst die optimalen und ungefähren Lösungen besser als DSN1;
* Durch gleichwertiges Zusammenführen von Etiketten und Ausbalancieren von Stichproben kann die Robustheit des Algorithmus verbessert werden.
Erste,DeepSymNet kann Ausdrücke effizienter darstellen als symbolische Bäume, und für dasselbe Modul, das mehrmals in einem Ausdruck vorkommt, ist die durchschnittliche Beschriftungslänge von DeepSymNet kürzer als die von NeSymRes.

Die Vorhersagegenauigkeit des mit DeepSymNet-Labels trainierten Modells übertrifft die des mit NeSymReS-Labels trainierten Modells bei weitem, wie in der obigen Abbildung gezeigt. Dies zeigt, dass DeepSymNet-Beschriftungen besser sind als symbolische Baumbeschriftungen.
Zweitens,Mit zunehmender Anzahl der vom Ausdruck belegten verborgenen Schichten nimmt die Vorhersagegenauigkeit des Modells rapide ab. Daher schlug das Forschungsteam vor, die Etikettenvorhersage in zwei Unteraufgaben aufzuteilen: Operatorvorhersage und Vorhersage der Verbindungsbeziehung, um sicherzustellen, dass das Problem der Etikettenvorhersage besser gelöst werden kann.

Die Ergebnisse des zweiteiligen Trainings von DeepSymNet zeigen, dass mit zunehmender Anzahl verborgener Schichten die Vorhersagegenauigkeit der Operatorauswahl stark abnimmt, während die Vorhersagegenauigkeit der Verbindungsbeziehungen hoch bleibt. Dies liegt daran, dass der Operatorauswahlraum viel größer ist als der Auswahlraum für Verbindungsbeziehungen. Um die Genauigkeit der Operatorauswahl zu verbessern, führten die Forscher daher ein separates Training zur Operatorauswahl durch.

Während des Vorhersageprozesses verwendete das Team zunächst das Operatorauswahlmodell, um die Operatorauswahlsequenz zu erhalten, und gab sie dann in das trainierte Modell DSN1 ein, um die Verbindungsbeziehung vorherzusagen. Die Testergebnisse sind in der Abbildung oben dargestellt. Nach einem separaten Training zur Operatorauswahl verbesserte sich die Vorhersagegenauigkeit erheblich. Das separat trainierte Modell heißt DSN2.
Darüber hinaus führten die Forscher Ablationsexperimente durch, um die Robustheit der äquivalenten Etikettenzusammenführung und der Verbesserung des Probenausgleichs zu überprüfen. Zunächst wurden 500.000 Trainingsbeispiele zufällig ausgewählt, die 128.455 verschiedene Bezeichnungen enthielten (TrainDataOrg). Die Ergebnisse zeigen, dass die Stichprobennummern dieser Etiketten stark ungleichmäßig verteilt sind. Die minimale Stichprobennummer beträgt 1, die maximale Stichprobennummer 13.196 und die Stichprobennummernvarianz 13.012,29.

Anschließend hat das Team die Anzahl der Beispiele ausgeglichen, um nach dem Zusammenführen gleichwertiger Bezeichnungen die Trainingsbeispiele TrainDataB und TrainDataBM zu erhalten.
Anschließend wurden auf Grundlage der drei Trainingsdaten die Modelle DSNOrg, DSNB und DSNBM erstellt. Diese drei Modelle wurden auf dem Testset getestet. Die Genauigkeit der drei Modelle nahm von Anfang bis Ende zu.Dies zeigt, dass nach der Erhöhung der Stichprobenbalance und der Zusammenführung gleichwertiger Beschriftungen die Genauigkeit des Modells beim Finden der optimalen Lösung verbessert wurde, was tatsächlich die Robustheit des Algorithmus erhöht und die Leistung des Algorithmus verbessert hat.
- Testergebnisse des öffentlichen Datensatzes
Das Forschungsteam verwendete 6 Testdatensätze:Koza , Korns, Keijzer, Vlad, ODE und AIFeynman wählten zum Testen Ausdrücke mit nicht mehr als 3 Variablen aus diesen Datensätzen aus. Ein Vergleich mit derzeit gängigen Methoden des überwachten Lernens zeigt, dass die Genauigkeit der vorgeschlagenen Algorithmen (DSN1, DSN2) den Vergleichsalgorithmen überlegen ist.
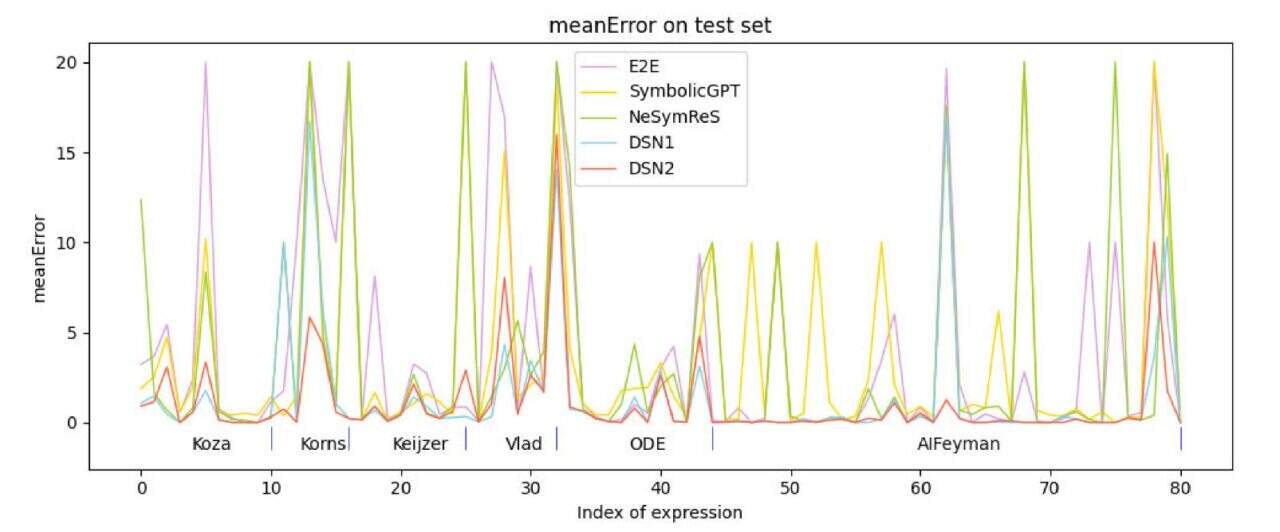
Darüber hinaus verglich das Team den Algorithmus mit den derzeit gängigen suchbasierten Methoden EQL, GP und DSR. Die Ergebnisse sind in der folgenden Abbildung dargestellt.
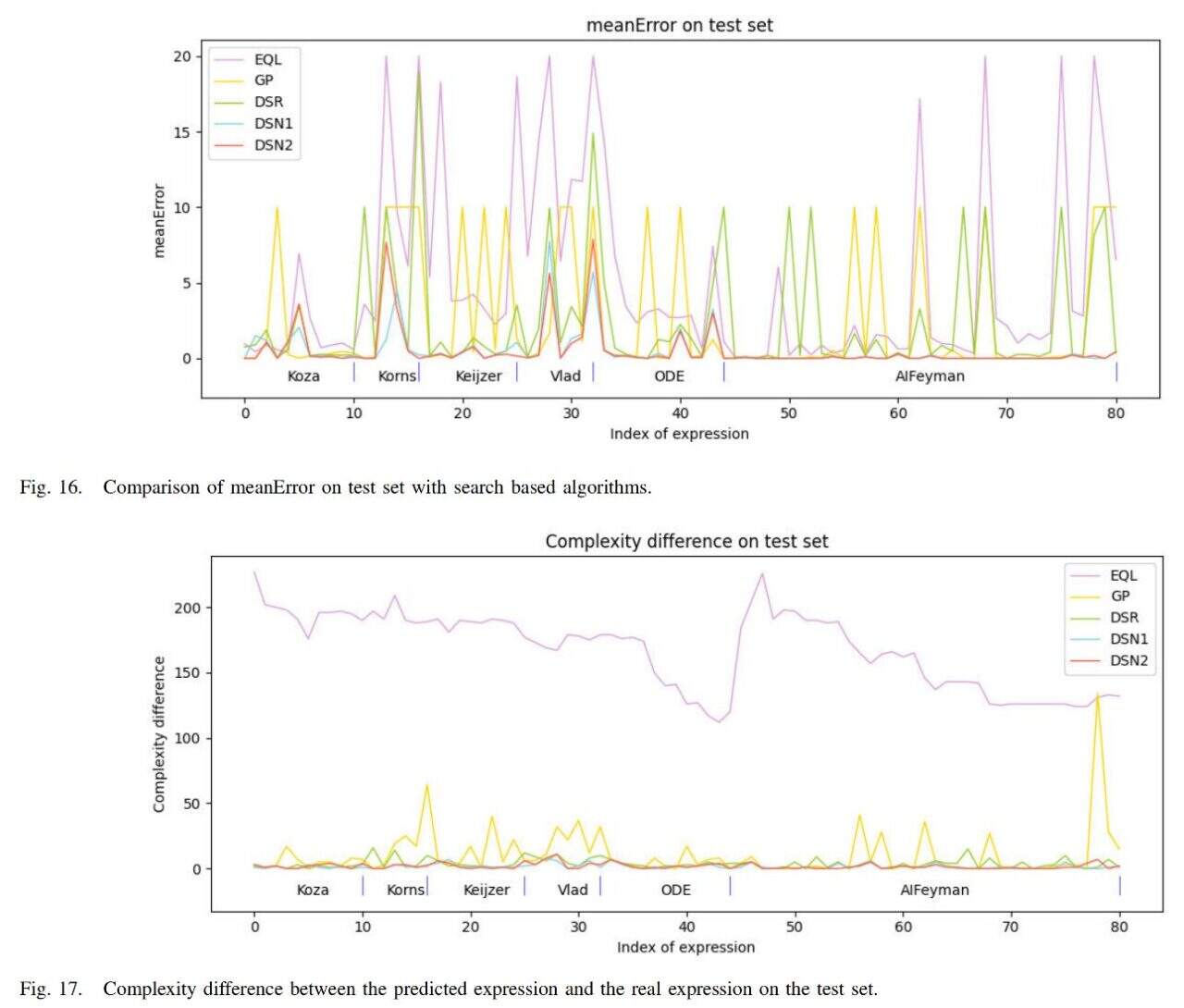
Der durchschnittliche Fehler des Algorithmus (DSN1, DSN2) ist am geringsten und die Komplexität des erhaltenen Ausdrucks kommt der Komplexität des wahren Ausdrucks am nächsten.
Zusammenfassend kann man aufgrund der Ergebnisse feststellen, dassDer vom Team untersuchte Algorithmus übertrifft die Vergleichsalgorithmen in drei Aspekten: symbolischer Ausdrucksfehler, symbolische Ausdruckskomplexität und Ausführungsgeschwindigkeit, was die Wirksamkeit des Algorithmus bestätigt.
Das Team hinter den Kulissen ist mit Stars besetzt
Wissenschaftler auf der ganzen Welt arbeiten intensiv an den Kernfragen der symbolischen Regression. Obwohl in dem Artikel erwähnt wird, dass DeepSymNet noch einige Einschränkungen aufweist, leistet diese Forschung dennoch einen wichtigen Beitrag zur künstlichen Intelligenz bei der Lösung mathematischer Probleme. Indem es als Klassifizierungsproblem behandelt wird, bietet es zweifellos eine neue Lösung für SR-Methoden, die auf überwachtem Lernen basieren.
Natürlich ist dieser Erfolg untrennbar mit der Leidenschaft und dem Schweiß einer Gruppe von Menschen verbunden, wie beispielsweise Wu Min, dem Erstautor des Artikels. Laut der offiziellen Website des Instituts für Halbleiter der Chinesischen Akademie der WissenschaftenWu Min ist derzeit Assistenzforscher am Institut für Halbleiter der Chinesischen Akademie der Wissenschaften. Er hat an mehreren wissenschaftlichen Forschungsprojekten teilgenommen, darunter „Symbolische Regression basierend auf Deep Learning und ihre Anwendung in der Forschung und Entwicklung von Halbleiterbauelementen“ und „Symbolische Regressionsmethode zur Vereinfachung der Teile-und-herrsche-Methode mit neuronalen Netzwerken zur Wissensfusion“.
Zusätzlich,Dr. Jingyi Liu, einer der Autoren des Artikels, war der Erstautor eines Artikels, der im Juli letzten Jahres in der führenden Fachzeitschrift für künstliche Intelligenz, Neural Networks, veröffentlicht wurde. Der Titel des Artikels lautete „SNR: Symbolic Network-based Rectifiable Learning Framework for Symbolic Regression“.Für das symbolische Regressionsproblem wird ein Lernrahmen mit Korrekturmöglichkeiten bereitgestellt.
Gemessen an der Forschung zu verwandten Themen ist das Land bei innovativen Methoden eindeutig führend. Zukünftig ist zu erwarten, dass diese Theorien und Forschungsergebnisse sicherlich schon in naher Zukunft wichtige Beiträge zur Lösung praktischer Probleme leisten werden.