Command Palette
Search for a command to run...
AlphaGeometry: Die Enorme Rechenleistung Von DeepMind Bewirkt Erneut Wunder, Aber „Rechenleistung Statt Intelligenz“ Ist Möglicherweise Nicht Die Optimale Lösung

Autor: Li Baozhu
Herausgeber: Sanyang
Quelle des Titelbildes: Google DeepMind
DeepMind nutzt Rechenleistung, um Wunder zu vollbringen? Wie wertvoll ist das hochgelobte AlphaGeometry?
Vor Kurzem wurde der Alpha-Reihe von Google DeepMind ein neues Mitglied hinzugefügt: AlphaGeometry, das sich immer noch großer Beliebtheit erfreut und dessen Bildschirm mit Lobeshymnen wie „Meilenstein“, „episch“ und „menschennah“ überflutet wird. Welchen Wert hat also dieses KI-System, das behauptet, über Fähigkeiten auf Goldmedaillenniveau bei Mathematik-Olympiaden zu verfügen?
AlphaGeometry wurde vom Google DeepMind-Team und Forschern der New York University entwickelt.Durch die Kombination eines neuronalen Sprachmodells mit einer symbolischen DeduktionsmaschineKann komplexe Geometrieprobleme auf einem Niveau lösen, das dem des Menschen nahe kommt.
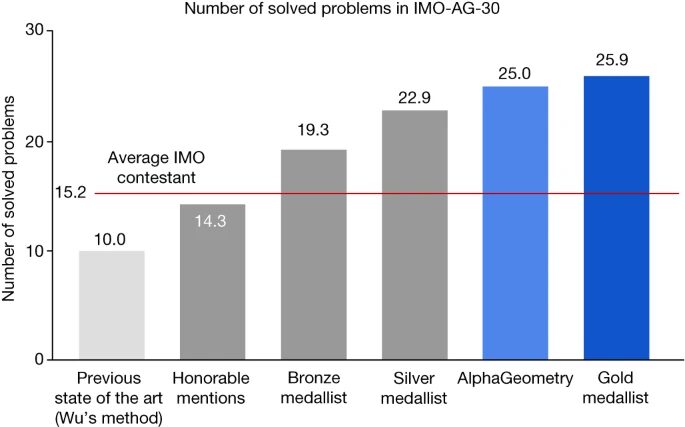
In einem Benchmark-Test von 30 Geometrieproblemen der Internationalen Mathematik-Olympiade (IMO) löste AlphaGeometry 25 davon in der vorgegebenen Zeit, die zuvor SOTA Mit Wus „Wu-Methode“ wurden 10 Probleme gelöst, während der menschliche IMO-Goldmedaillengewinner durchschnittlich 25,9 Probleme lösen konnte.
Tatsächlich hat sich seit der Einführung von AlphaGo, begleitet von zahlreichen innovativen Durchbrüchen in unterschiedlichen Disziplinen, die Positionierung „DeepMind-Produkte müssen von hoher Qualität sein“ allmählich in den Köpfen der Menschen verankert. Gleichzeitig gibt es in der Branche aber auch rationale und dialektische Stimmen: Der Ersatz von Intelligenz durch Rechenleistung ist sicherlich erfreulich, aber der tatsächliche Anwendungswert ist wichtiger. Daher möchten wir mit der Veröffentlichung von AlphaGeometry kurz diskutieren, ob es sich hier um einen Karneval unter dem Vorteil der Rechenleistung handelt, oder KI für die Wissenschaft Pfadfinder.
Es ist erwähnenswert, dassWir interviewten Professor der School of Intelligence an der Peking-UniversitätLin Zhouchen, und relevante akademische Fragen diskutiert und studiert.Professor Lin Zhouchen studierte Mathematik und angewandte Mathematik an der Nankai-Universität, der Peking-Universität und der Hong Kong Polytechnic University und kehrte dann an die School of Mathematics der Peking-Universität zurück, um dort einen Doktortitel zu erwerben und sich im Bereich der künstlichen Intelligenz zu engagieren. (Klicken Sie hier, um das Interview mit Professor Lin Zhouchen anzusehen)
Ausdruck und Berechnung: zwei große Herausforderungen der KI für die Mathematik
Professor Lin Zhouchen sagte:„In der Vergangenheit waren der „Ausdruck“ mathematischer Theoreme und das Rechnen im großen Maßstab die beiden größten Herausforderungen für die KI, um mathematische Theoreme zu beweisen.“
Da es sich in der Mathematik um ein sehr abstraktes Fach handelt, das stark auf logischem Denken beruht, besteht der erste Schritt zur Nutzung von KI darin, das Ausdrucksproblem zu lösen. Mathematische Theoreme so auszudrücken, dass sie computerberechnen können, ist die Grundlage für spätere KI-Anwendungen.
Die geometrischen Probleme, auf die sich AlphaGeometry konzentriert, sind relativ einfach auszudrücken. Das Aufkommen der analytischen und algebraischen Geometrie hat es möglich gemacht, geometrische Formen und die Beziehung zwischen geometrischen Objekten durch numerische Werte auszudrücken.Wu WenjunDer "Mathematische Mechanisierung„, und bis zu einem gewissen Grad baute es auch eine Brücke zwischen Theoremen der ebenen Geometrie und der Maschinensprache.“
„Zweitens haben die von Akademiemitglied Wu Wenjun vorgeschlagene ‚Wu-Methode‘ und traditionelle Methoden wie die Gröbner-Basis das Problem des Beweises von Theoremen der ebenen Geometrie theoretisch gelöst, sind jedoch durch die Rechenleistung begrenzt. Mit anderen Worten: Aufgrund des großen Speicher- und Rechenaufwands wächst der Operationsraum exponentiell, insbesondere bei schwierigeren Problemen der ebenen Geometrie, sodass viele frühere Methoden Schwierigkeiten bei der Bewältigung schwieriger Probleme haben.“
Das Problem des großen Rechenaufwands ist für DeepMind, das über reichlich Geld verfügt, offensichtlich nicht das Haupthindernis. Die Hauptschwierigkeit besteht darin, das exponentielle Wachstum des Betriebsraums zu vermeiden, und hier können Methoden des maschinellen Lernens hilfreich sein. „
Insbesondere wird AlphaGeometry anhand von 100 Millionen synthetischen Datenpunkten trainiert, kann komplexe geometrische Herausforderungen ohne menschliche Demonstration autonom lösen und für Menschen lesbare Beweise generieren.
Wie in der folgenden Abbildung gezeigt, müssen Sie, wenn Sie den „Satz von gleichschenkligen Körpern“, der den Grund- und Sekundarschülern in meinem Land am vertrautesten ist, als Beispiel nehmen, dass Sie, wenn Sie beweisen möchten, dass ∠ABC=∠BCA ist, das Problem zuerst manuell in eine Computersprache konvertieren und es dann in AlphaGeometry eingeben müssen.
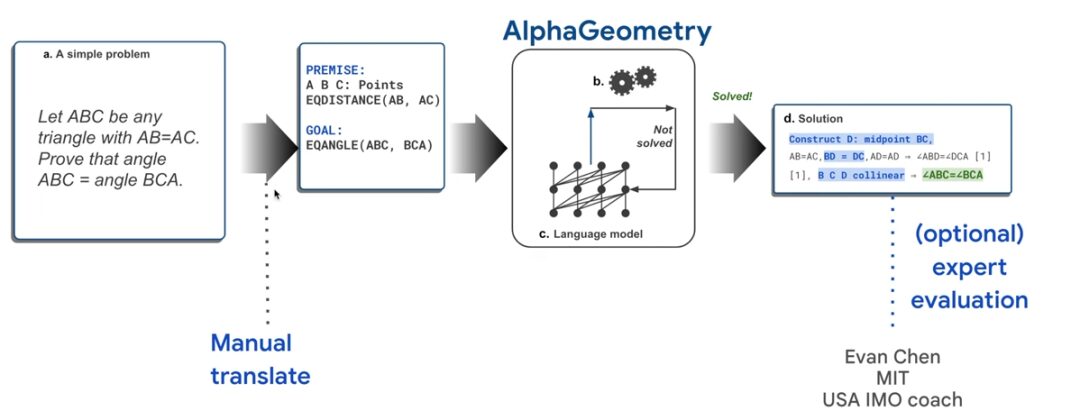
AlphaGeometry leitet die Beweissuche ein, indem es eine symbolische Deduktionsmaschine ausführt, die „erschöpfend“ neue Aussagen aus den Theoremprämissen ableitet, bis das Theorem bewiesen ist oder keine neuen Aussagen mehr möglich sind. Wenn die symbolische Deduktionsmaschine keinen Beweis findet, konstruiert das Sprachmodell einen Hilfspunkt, fügt beweisbare Bedingungen hinzu und startet die Suche nach einem Beweis durch die symbolische Maschine neu. Dieser Zyklus wird fortgesetzt, bis eine Lösung gefunden ist.
Lösungen werden automatisch in eine für Menschen lesbare Sprache analysiert, sodass sie überprüft und ausgewertet werden können.
Es ist erwähnenswert, dass AlphaGeometry synthetische Daten für das Modelltraining verwendet und so das Problem des Mangels an relevanten Datenbanken löst.
Indem sie die vorhandene symbolische Engine auf verschiedene zufällige Theoremprämissen anwandten und sie 72 Stunden lang auf 100.000 CPUs laufen ließen, erhielten die Forscher ungefähr 500 Millionen synthetische Theorembeweisbeispiele. Nach der formalen Normalisierung und Deduplizierung erhielten sie schließlich 100 Millionen Beispiele für Theorembeweise, von denen 9 Millionen Beispiele mindestens eine Hilfskonstruktion beinhalteten, und viele Beweisschritte überschritten 200, was dem Vierfachen der durchschnittlichen Beweislänge von Geometrieproblemen bei der Internationalen Mathematik-Olympiade entspricht.
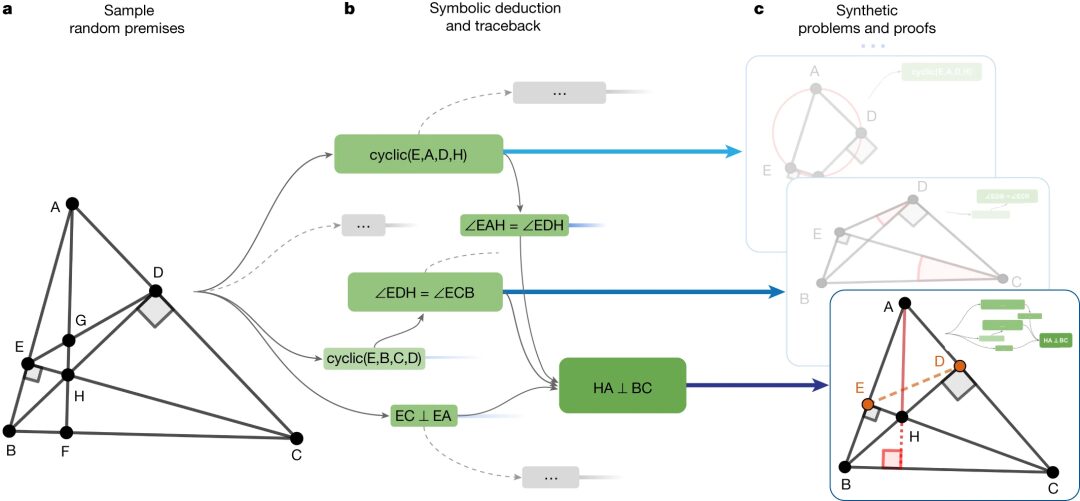
Um die Fähigkeit von AlphaGeometry zur Lösung praktischer Probleme zu vergleichen und zu testen, versuchten die Forscher, Geometrieprobleme des IMO-Wettbewerbs seit 2000 in eine für symbolische Engines lesbare Maschinensprache zu konvertieren. Dabei stellten sie fest, dass nur 75% erfolgreich ausgedrückt werden konnten. Dadurch entstand ein Testsatz IMO-AG-30, der aus 30 klassischen Geometrieproblemen besteht.
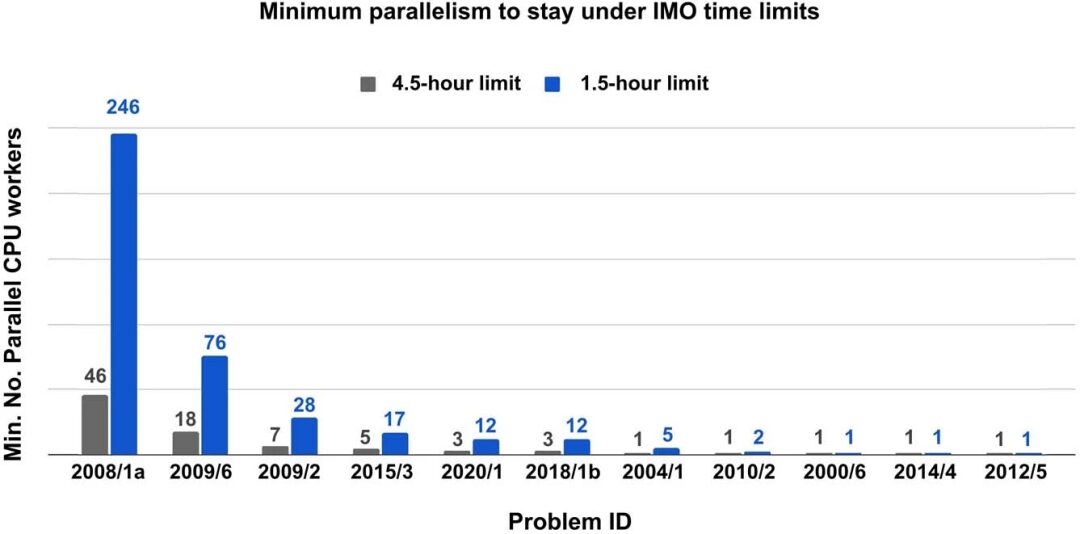
Jedes Problem hat eine andere Laufzeit, da die Größe seines Ableitungsabschlusses unterschiedlich ist. Die Forscher stellten fest, dass die Laufzeit nicht mit der Schwierigkeit des Problems korrelierte. Beispielsweise ist IMO 2019 P6 viel schwieriger als IMO 2008 P1a, erfordert jedoch viel weniger Parallelisierungszeit, um es innerhalb des IMO-Zeitlimits zu lösen.
Da der Dekodierungsprozess des Sprachmodells k verschiedene Sequenzen zurückgibt, die k optionale Hilfsstrukturen beschreiben, führten die Forscher eine Strahlensuche für die k Optionen durch und verwendeten dabei die Punktzahl jedes Strahls als Wertfunktion. Diese Methode weist eine starke Parallelität auf und kann die Suchgeschwindigkeit erheblich verbessern, wenn parallele Rechenressourcen verfügbar sind.
Die Forscher fanden heraus, dass die Mindestanzahl paralleler CPUs, die erforderlich ist, um alle 25 Probleme zu lösen und mit vier parallelen Kopien des GPU V100-beschleunigten Sprachmodells innerhalb des Zeitlimits zu bleiben, in der folgenden Abbildung dargestellt ist:
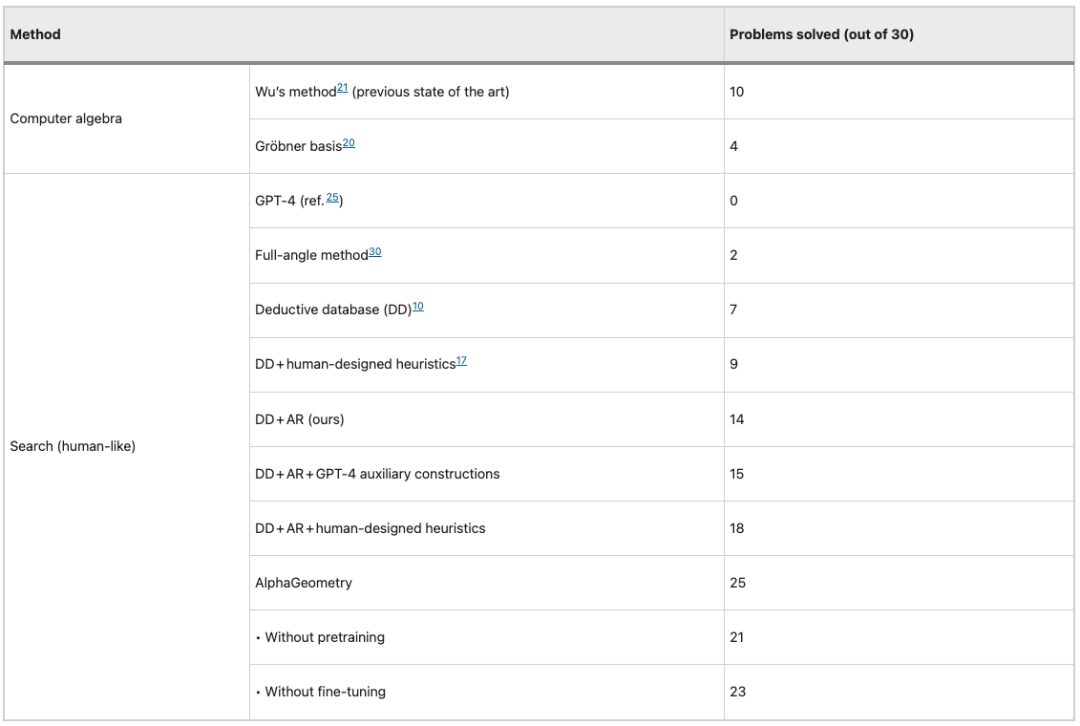
Die Leistung von 10 verschiedenen Modellen/Methoden im Testsatz IMO-AG-30 ist in der folgenden Abbildung dargestellt. Interessanterweise hat GPT-4 im Test keine einzige Frage richtig beantwortet.
Hinter der Substitution von Intelligenz durch Rechenleistung steht der Anwendungswert
In den letzten zwei Tagen haben die überwältigenden Berichte im Internet die Erfolge von AlphaGeometry vollständig offengelegt. Ihr Einfluss bedarf keiner weiteren Erläuterung, daher möchten wir nach all dem Lärm untersuchen, welchen praktischen Wert AlphaGeometry für die wissenschaftliche Forschung und die Entwicklung von KI-Anwendungen haben kann.
Professor Lin Zhouchen sagte:Derzeit kann AlphaGeometry wie AlphaGo zu einem „Lehrer“ werden und eine größere unterstützende Rolle beim Unterrichten spielen.Darüber hinaus ist der Durchbruch von AlphaGeometry in Bezug auf die Modellleistung unbestreitbar und zeigt erneut, dass „große Leistung Wunder bewirken kann“ – der enorme Rechenleistungsvorteil führt zu einer starken Modellleistung, die in gewissem Maße das Vertrauen von Forschern und Unternehmen, die Rechenleistung „vergöttern“, weiter stärkt. „
Doch wie Professor Lin Zhouchen sagte:Obwohl wir im Bereich der KI schon unzählige Male erlebt haben, wie effektiv „Rechenleistung Intelligenz ersetzt“, ist der endgültige Durchbruch auf dem Weg zum Branchenexperten mit KI immer noch schwer zu erreichen.
Daher sind sie, egal ob es sich um AlphaGeometry oder andere KI-Tools wie das GPT-Modell handelt, vorerst immer noch „Lehrer und Freunde“ im täglichen Leben der Menschen und in der wissenschaftlichen Forschung. Der flexible Einsatz von KI-Tools ist zu einem allgemeinen Trend geworden. Die Anwendung der durch die Rechenleistung geschaffenen „Wunder“ auf praktische Probleme ist ein Wert, den der Mensch nur schwer ersetzen kann.
Wenn man aus der Vergangenheit Lehren zieht und diese auf die Gegenwart anwendet, weist der schnelle Aufstieg von KI-Tools viele Ähnlichkeiten mit der Popularisierung von Computern auf. Beispielsweise hat sie unsere Arbeitsweise revolutioniert, indem sie traditionelle Methoden mit großer Dynamik ersetzt und sich allmählich zu einem Kriterium für die Beurteilung der Leistungsfähigkeit am Arbeitsplatz entwickelt hat. Im Gegensatz dazu sind jedoch auch die Einschränkungen von KI-Tools ausgeprägter, nämlich die Spezifität.
Professor Lin Zhouchen glaubt:Den aktuellen KI-Tools fehlt es an EinheitlichkeitSelbst wenn wir uns nur auf die Mathematik konzentrieren, besteht ein großer Unterschied zwischen KI-Tools, die für die Zahlentheorie und Geometrie entwickelt wurden, ganz zu schweigen von interdisziplinären KI-Tools. KI-Tools sind noch nicht so zugänglich wie die grundlegende Infrastruktur, die Computer heute darstellen. Zu den aktuellen Computersprachen gehören C, Java, Python usw. Es ist durchaus möglich, Probleme in mehreren Disziplinen wie Mathematik, Physik, Chemie usw. auf der Grundlage einer dieser Sprachen zu lösen, was ihre Vielseitigkeit widerspiegelt. Bei KI-Tools ist dies jedoch nicht der Fall, wie die Alpha-Serie zeigt. „
Daher ist Professor Lin Zhouchen davon überzeugt: „Wenn KI-Tools in Zukunft abstrahiert und wiederverwendet werden können, wird sich KI in der Wissenschaft durchsetzen können.“ „
Dies ist auch ein Phänomen, das HyperAI bei der kontinuierlichen Verfolgung der Entwicklung der KI für die Wissenschaft beobachtet hat. Einige Forschungsgruppen oder Forschungsteams rekrutieren zusätzlich zu den Mitgliedern der Disziplin ein auf KI spezialisiertes Mitglied, das für die Entwicklung der für die Forschung erforderlichen KI-Tools verantwortlich ist, während der wissenschaftliche Teil weiterhin den traditionellen wissenschaftlichen Forschern überlassen bleibt.
Es besteht kein Zweifel daran, dass die Unterstützung und Verbesserung des wissenschaftlichen Forschungsprozesses durch KI immer offensichtlicher wird und sich zu einem neuen Trend entwickelt. Ist dieses KI+Wissenschaftsteammodell jedoch eine langfristige Lösung?
Professor Lin Zhouchen ist davon überzeugt: „In Zukunft müssen einerseits die Hemmschwellen für den Einsatz von KI-Tools gesenkt und ein gewisses Maß an Einheitlichkeit erreicht werden, damit Wissenschaftler die Komponenten von KI-Tools auch für unterschiedliche Probleme kombinieren und nutzen können, genau wie bei der Computerprogrammierung. Andererseits müssen Wissenschaftler auch ihre Fähigkeiten im Umgang mit KI-Tools schrittweise verbessern, um das volle Potenzial der KI auszuschöpfen.“
Der Weg ist lang und schwierig, aber wenn Sie weitermachen, werden Sie Ihr Ziel erreichen. „AI for Science“ wurde von großen Unternehmen wie DeepMind initiiert und hat mit der Förderung durch die nationale Politik eine lange Reise begonnen. Die Hindernisse auf diesem Weg müssen von der wissenschaftlichen Forschung und der Industrie gemeinsam überwunden werden, um bei der Umsetzung wirklich einen Mehrwert für die menschliche Entwicklung zu schaffen.
Abschließend möchte ich Professor Lin Zhouchen von der School of Intelligence der Peking-Universität für seine Hilfe und Unterstützung beim Verfassen dieses Artikels danken. Derzeit sucht die Forschungsgruppe von Professor Zhouchen Lin Doktoranden. Studierende, die die Voraussetzungen erfüllen, können ihren Lebenslauf gerne an [email protected] senden.
Ich lebe nach dem Credo des Physikers Ludwig Boltzmann: Nichts ist praktischer als eine gute Theorie. Ich bin nun auf der Suche nach Doktoranden mit guten Kenntnissen in Mathematik (das heißt aber nicht, dass sie aus einem mathematischen Fachbereich kommen müssen) und großem Interesse an theoretischer Analyse, damit sie gemeinsam mit mir lernen können, wie man Mathematik elegant zur Lösung praktischer Probleme einsetzt. Senden Sie mir gerne Ihren Lebenslauf.
——Lin Zhouchen