HyperAI
StartseiteNeuigkeitenNeueste ForschungsarbeitenTutorialsDatensätzeVeranstaltungenWikiSOTALLM-Modelle
Suche
Über
HyperAI

PyTorch-Matrixmultiplikationsmethode – Zusammenfassung Und Problemlösung

vor 4 Jahren
Information
Rollroll Yuan
特色图像


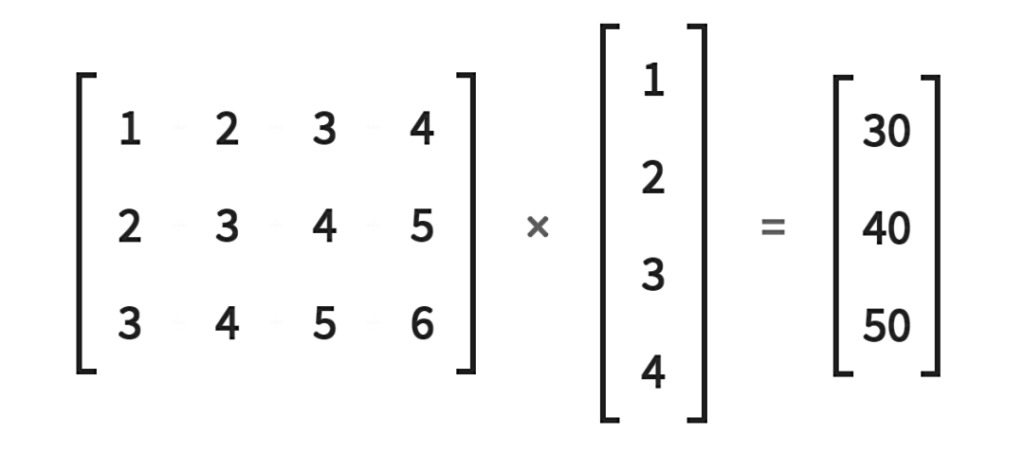
Beim maschinellen Lernen und Deep Learning sind Matrixoperationen die häufigste und effektivste Methode zur Verbesserung der Rechenleistung. Da Merkmale und Gewichte als Vektoren gespeichert werden, sind Matrixoperationen besonders wichtig.Wichtige Methoden des maschinellen Lernens wie Gradientenabstieg, Backpropagation und Matrixfaktorisierung erfordern alle Matrixoperationen.


Beim Deep Learning speichern neuronale Netzwerke Gewichte in Matrizen, und auf linearer Algebra basierende Operationen auf der GPU können einfache und schnelle Berechnungen an den Matrizen durchführen.

Kleinere Matrixoperationen können mithilfe von For-Schleifen schnell berechnet werden. Aber wenn Sie auf eine riesige Datenmenge stoßen,Schleifenanweisungen verlangsamen die Berechnungsgeschwindigkeit.Derzeit verwenden wir häufig die Matrizenmultiplikation, die die Effizienz der Berechnungen erheblich verbessern kann.

Gängige Methoden der Matrix-, Vektor- und Skalarmultiplikation

  • Fackel (mm) 2D-Matrixmultiplikation

torch.mm(mat1,ma2,out=None), wobei mat1(n*m), mat2(m*d), die Dimension der Ausgabe out ist (n*d).
Hinweis: Berechnet die Matrixmultiplikation zweier 2D-Matrizen und unterstützt kein Broadcasting.

  • torch.bmm() 3D-Batch-Matrixmultiplikation

torch.bmm(bmat1,bmat2,out=None), wobei bmat1(b*n*m), bmat2(B*m*d), die Ausgabe out hat eine Dimension von (B*n*d).
Hinweis: Die beiden Eingaben dieser Funktion müssen dreidimensionale Matrizen mit derselben ersten Dimension sein (die die Batch-Dimension angibt). Übertragung wird nicht unterstützt.

  • torch.matmul() gemischte Matrixmultiplikation 

torch.matmul(input,other,out=None), diese Methode ist komplizierter und es wird empfohlen, das Dokument zu konsultieren. Es ist das Matrixprodukt zweier Tensoren. Das Berechnungsergebnis hängt von der Dimension des Tensors ab und unterstützt die Übertragung.

  • torch.mul() Matrixelementweise Multiplikation 

torch.mul(mat1,other,out=None), wobei der andere Multiplikator ein Skalar oder eine Matrix beliebiger Dimension sein kann, solange die endgültige Multiplikation erfüllt ist und Broadcasting unterstützt wird.

  • torch.mv() Matrix-Vektor-Multiplikation

torch.mv(mat, vec, out=None) multipliziert die Matrix mat und den Vektor vec. Wenn mat ein n×m-Tensor und vec ein m-elementiger 1D-Tensor ist, ist die Ausgabe ein n-elementiger 1D-Tensor ohne Broadcasting-Unterstützung.

  • torch.dot() Tensor-Punktmultiplikation

torch.dot(tensor1, tensor2) berechnet das Skalarprodukt zweier Tensoren. Beide Tensoren sind 1-D-Vektoren und unterstützen keine Übertragung.

Forum Heiße Fragen

 F: Wie multipliziert man Stapel von Datenvektoren, ohne eine For-Schleife zu verwenden?
Eingabeform: N x M x Vektorgröße Gewichtsform: M x Vektorgröße x Vektorgröße Zielausgabeform: N x M x Vektorgröße
N steht für die Batchgröße, M für die Anzahl der Vektoren und VectorSize für die Größe der Vektoren.
Wie in der folgenden Abbildung dargestellt: Lösung:

N, M, V=2, 3, 5a = torch.randn(N, M, V)b = torch.randn(M, V, V)a_expand = a.unsqueeze(-2)b_expand = b.expand(N, -1, -1, -1)​c = torch.matmul(a_expand, b_expand).squeeze(-2)

Ursprüngliche Postadresse:https://discuss.pytorch.org/t/batch-matrix-vector-multiplication-without-for-loop/112841
 

F: Bei der Berechnung der Matrix-Vektor-Multiplikation durch Batch-Vektor-Eingabe tritt ein RuntimeError auf 
Gegeben:

# (batch x inp)v = torch.randn(5, 15)# (inp x output)M = torch.randn(15, 20)

berechnen:

# (batch x output)out = torch.Tensor(5, 20)for i, batch_v in enumerate(v):    out[i] = (batch_v * M).t()

Allerdings führt (i) die Multiplikation bei zwei Eingaben derselben Dimension zu folgendem Fehler: RuntimeError: inconsistent tensor size at /home/enrique/code/vendor/pytorch/torch/lib/TH/generic/THTensorMath.c:623
Warum tritt dieser Fehler auf? Gibt es eine Möglichkeit, das Durchlaufen von Zeilenvektoren zu vermeiden?

  Lösung:
* steht für elementweise Multiplikation. Wenn Sie Python 3 verwenden, können Sie den @-Operator für die Matrix-Vektor-Multiplikation und die Matrix-Matrix-Multiplikation verwenden.

Sie können auch batch_v.mm(M) verwenden, da die gebündelte Vektormatrix eine Matrix-Matrix-Multiplikation ist.
Darüber hinaus können Sie auch Methoden wie bmm und baddbmm verwenden, um Schleifenoperationen in Python zu eliminieren.

Ursprüngliche Postadresse:https://discuss.pytorch.org/t/matrix-vector-multiply-handling-batched-data/203
 F: Wie berechnet man die Matrix-Vektor-Multiplikation ohne Verwendung von Schleifenanweisungen?
Wie können wir eine 2×2-Matrix mit drei Vektoren der Größe 2 multiplizieren, ohne Schleifen zu verwenden?

Bemerkung:
1. Bei Verwendung einer Schleifenanweisung lautet der Code wie folgt:

A=torch.tensor([[1.,2.],[3.,4.]])b=torch.tensor([[3.,4.], [5.,6], [7.,8.]])res = []for i in range(b.shape[0]):    res.append(torch.matmul(A, b[i]))

2. Nach dem Versuch funktioniert torch.matmul (A.repeat ((2,1,1)), b) nicht.

  Lösung:
Dies kann mit a.matmul(bt()) erreicht werden.
Ursprüngliche Postadresse:https://discuss.pytorch.org/t/vectorize-matrix-vector-multiplication/88051


Dieses offizielle Konto wird weiterhin die neuesten PyTorch-Informationen und Entwicklungskenntnisse aktualisieren, folgen Sie uns gerne!