Wenn Turing Der Vater Der KI Ist, Sollte Shannon Dann Der Onkel Der KI Sein?

Shannon war in seiner Jugend gutaussehend und selbstbewusst und außerdem ein entfernter Verwandter des Erfinders Edison.

Am 30. April 1916 wurde Claude Shannon in einer kleinen Stadt namens Gaylord, Michigan, USA, geboren. Zu dieser Zeit befand sich Turing weit weg im fernen England und war vier Jahre alt. Shannon erhielt 1936 einen Bachelor-Abschluss in Mathematik und Elektrotechnik von der University of Michigan. 1940 erhielt er einen Master- und Doktortitel in Mathematik vom MIT und kam 1941 zu Bell Labs.

Im Vergleich zu Turing verlief Shannons Leben reibungsloser. Er starb am 26. Februar 2001 im Alter von 84 Jahren.

Die von Shannon entwickelte Informationstheorie ist nicht nur der Eckpfeiler der Informations- und Kommunikationswissenschaft, sondern bleibt auch die wichtigsteEs ist eine wichtige theoretische Grundlage für Deep Learning.

Die Informationstheorie kombiniert Infinitesimalrechnung, Wahrscheinlichkeitstheorie, Statistik und andere Disziplinen und spielt beim Deep Learning eine sehr wichtige Rolle:

• Gemeinsame Kreuzentropieverlustfunktionen;

• Erstellen Sie einen Entscheidungsbaum basierend auf maximalem Informationsgewinn;

• Der Viterbi-Algorithmus wird häufig in NLP und Sprache verwendet.

• RNNs werden häufig in der maschinellen Übersetzung verwendet und Encoder und Decoder werden häufig in verschiedenen Arten von Modellen verwendet;

Beginnen wir mit einem einfachen Beispiel. Die folgenden beiden Sätze enthalten unterschiedlich viel Information.

„Bruno ist ein Hund.“

„Bruno ist ein großer brauner Hund.“

Es ist offensichtlich, dass die beiden Sätze unterschiedlich viel Information vermitteln. Im Vergleich zum ersten Satz enthält der zweite Satz mehr Informationen. Es verrät uns nicht nur, dass Bruno ein Hund ist, sondern verrät uns auch die Fellfarbe und Körperform des Hundes.

Doch diese beiden einfachen Sätze bereiteten Wissenschaftlern und Ingenieuren im frühen 20. Jahrhundert die größten Kopfschmerzen.

Sie wollten die Unterschiede zwischen diesen Informationen quantifizieren und mathematisch beschreiben.

Leider gab es damals keine leicht zugängliche analytische oder mathematische Methode, um dies zu tun.

Seitdem suchen Wissenschaftler nach der Antwort auf diese Frage und hoffen, die Antwort unter anderem aus Aspekten der Semantik der Daten zu finden. Doch es stellt sich heraus, dass derartige Untersuchungen keinem anderen Zweck dienen, als das Problem zu verkomplizieren.

Erst als Shannon, ein Mathematiker und Ingenieur, "Entropie"Nach dem Konzept. Das Problem der quantitativen Messung von Informationen ist endlich gelöst, was zugleich den Beginn unseres Eintritts in das „digitale Informationszeitalter“ markiert.

Shannon konzentrierte sich nicht auf die Semantik der Daten, sondern auf die Wahrscheinlichkeitsverteilung und "Unsicherheit"Um Informationen zu quantifizieren und einzuführen "bisschen"Das Konzept der Informationsmessung.

Er glaubt, dass die Semantik der Daten keine Rolle spielt, wenn es um den Informationsgehalt geht.

Diese revolutionäre Idee legte nicht nur den Grundstein für die Informationstheorie, sondern eröffnete auch neue Wege für die Entwicklung von Bereichen wie der künstlichen Intelligenz. Daher wird Claude Shannon auch als Vater des Informationszeitalters anerkannt.

Die Informationstheorie hat viele Anwendungsszenarien. Hier betrachten wir hauptsächlich die vier häufigeren Anwendungen in den Bereichen Deep Learning und Data Science.

Entropie

Auch als Informationsentropie oder Shannon-Entropie bekannt, wird sie zur Messung unsicherer Ergebnisse verwendet. Wir können es durch die folgenden zwei Experimente verstehen:

• Werfen Sie eine faire Münze, sodass die Wahrscheinlichkeit des Ergebnisses 0,5 beträgt.

• Werfen Sie eine manipulierte Münze, sodass die Wahrscheinlichkeit des Ergebnisses 0,99 beträgt.

Offensichtlich lassen sich die Ergebnisse von Experiment 2 leichter vorhersagen als die von Experiment 1. Aus den Ergebnissen lässt sich daher schließen, dass Experiment 1 unsicherer ist als Experiment 2, und die Entropie wird speziell zur Messung dieser Unsicherheit verwendet.

Wenn die experimentellen Ergebnisse mit größerer Unsicherheit behaftet sind, ist ihre Entropie höher und umgekehrt.

In einem deterministischen Experiment, bei dem das Ergebnis völlig sicher ist, ist die Entropie Null. Bei einem völlig zufälligen Experiment, wie zum Beispiel einem fairen Würfelspiel, besteht hinsichtlich jedes Ergebnisses eine große Unsicherheit, sodass die Entropie sehr groß sein wird.

Eine andere Möglichkeit zur Bestimmung der Entropie besteht darin, die Entropie als Funktion der durchschnittlichen Informationen zu definieren, die bei der Beobachtung der Ergebnisse eines Zufallsexperiments erhalten werden. Je weniger Ergebnisse vorliegen, desto weniger Informationen werden beobachtet und desto geringer ist die Entropie.

Beispielsweise kennen wir bei einem deterministischen Experiment immer das Ergebnis, so dass durch die Beobachtung des Ergebnisses keine neuen Informationen gewonnen werden und die Entropie somit Null ist.

Mathematische Formel

Für eine diskrete Zufallsvariable X werden die möglichen Ergebnisse als x_1, ..., x_n aufgezeichnet. Die Formel zur Berechnung der Entropie lautet dann wie folgt (Entropie wird durch H, Einheitsbit, dargestellt):

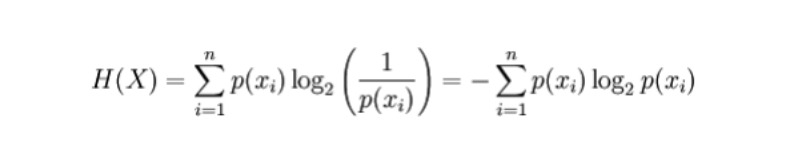
Wobei p(x_i) die Wahrscheinlichkeit des durch die Variable X erzeugten Ergebnisses ist.

Anwendung

• Erstellen Sie einen automatischen Entscheidungsbaum. Während des Konstruktionsprozesses kann die gesamte Merkmalsauswahl mithilfe des Entropiekriteriums erfolgen.

• Je größer die Entropie, desto mehr Informationen sind vorhanden und desto höher ist ihr Vorhersagewert. Auf dieser Grundlage kann aus den beiden konkurrierenden Modellen das wertvollste Modell, also das Modell mit der höchsten Entropie, ermittelt werden.

Kreuzentropie

Definition:Kreuzentropie wird hauptsächlich verwendet, um die Differenzinformationen zwischen zwei Wahrscheinlichkeitsverteilungen zu messen. Es kann uns sagen, wie ähnlich die beiden Wahrscheinlichkeiten sind.

Mathematische Formel

Die Formel zur Berechnung der Kreuzentropie für zwei Wahrscheinlichkeiten p und q, die in derselben Stichprobe definiert sind, lautet (Entropie wird durch H, Einheitsbit, dargestellt):

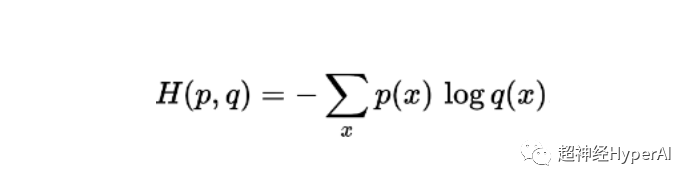
Anwendung

• Die Kreuzentropieverlustfunktion wird häufig in Klassifizierungsmodellen wie der logistischen Regression verwendet. Wenn die Vorhersage vom tatsächlichen Ergebnis abweicht, erhöht sich die Kreuzentropieverlustfunktion.

• In Deep-Learning-Architekturen wie CNNs verwendet die endgültige Ausgabeschicht „Softmax“ häufig eine Cross-Entropy-Loss-Funktion.

Abbildung 1: CNN-basierte Klassifikatoren verwenden normalerweise die Softmax-Schicht als letzte Schicht und nutzen die Cross-Entropy-Loss-Funktion zum Training.

Gegenseitige Information

Definition: Gegenseitige Information wird verwendet, um den Grad der gegenseitigen Abhängigkeit zwischen zwei Wahrscheinlichkeitsverteilungen oder Zufallsvariablen zu messen. Einfach ausgedrückt geht es darum, wie viele Informationen eine Variable mit sich trägt.

Die durch gegenseitige Information erfasste Korrelation zwischen Zufallsvariablen unterscheidet sich von der allgemeinen Korrelation, die auf das lineare Feld beschränkt ist. Es kann auch einige nichtlineare verwandte Informationen erfassen und verfügt über ein breiteres Anwendungsspektrum.

Mathematische Formel

Die Formel für die gegenseitige Information zweier diskreter Zufallsvariablen X und Y lautet:

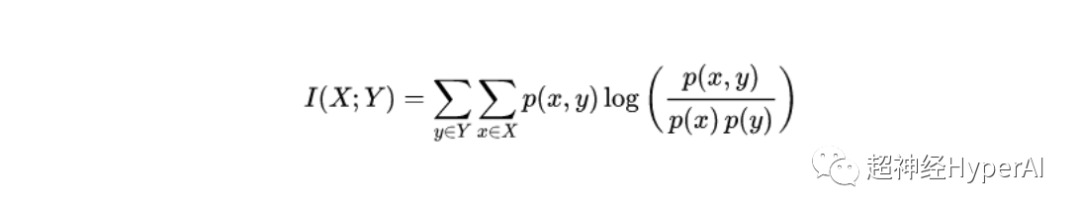
Dabei ist p(x,y) die gemeinsame Wahrscheinlichkeitsverteilung von x und y und p(x) und p(y) sind die Randwahrscheinlichkeitsverteilungen von x bzw. y.

Anwendung

• Merkmalsauswahl: Durch gegenseitige Information können nicht nur lineare Korrelationen erfasst, sondern auch nichtlineare Korrelationen berücksichtigt werden, wodurch die Merkmalsauswahl umfassender und genauer wird.
• In Bayes-Netzwerken wird gegenseitige Information verwendet, um die Beziehungsstruktur zwischen Zufallsvariablen zu lernen und die Stärke dieser Beziehungen zu definieren..

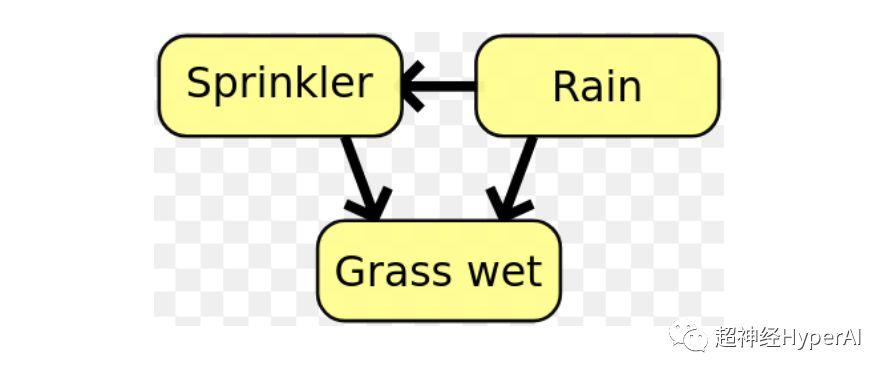
Abbildung 1: In einem Bayes-Netzwerk kann die Beziehungsstruktur zwischen Variablen mithilfe gegenseitiger Information bestimmt werden.

KL-Divergenz (Kullback-Leibler-Divergenz)

Die KL-Divergenz, auch als relative Entropie bekannt, wird verwendet, um den Grad der Abweichung zwischen zwei Wahrscheinlichkeitsverteilungen zu messen.

Angenommen, die benötigten Daten liegen in der wahren Verteilung P, aber wir kennen dieses P nicht. In diesem Fall können wir eine neue Wahrscheinlichkeitsverteilung Q erstellen, die zur wahren Verteilung P passt.

Da die Daten in Q nur annähernd P entsprechen, ist Q nicht so genau wie P. Daher gehen in Q im Vergleich zu P einige Informationen verloren, und das Ausmaß dieses Informationsverlusts wird durch die KL-Divergenz gemessen.

Die KL-Divergenz gibt an, wie viele Informationen wir verlieren, wenn wir uns für die Verwendung von Q (eine Näherung von P) entscheiden. Je näher die KL-Divergenz bei Null liegt, desto näher liegen die Daten in Q bei P.

Mathematische Formel

Die mathematische Formel für die KL-Divergenz einer Wahrscheinlichkeitsverteilung Q mit einer anderen Wahrscheinlichkeitsverteilung P lautet:

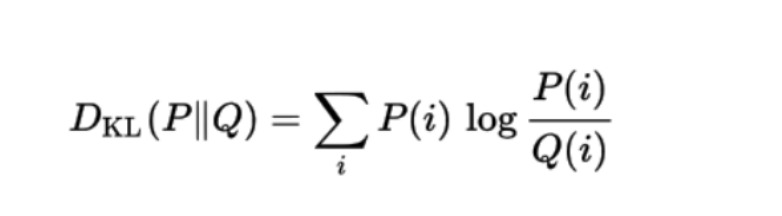
Anwendung

KL-Divergenz wird derzeit in VAE (Variational Autoencoder) in unüberwachten maschinellen Lernsystemen verwendet.

Im Jahr 1948 schlug Claude Shannon in seinem bahnbrechenden Aufsatz „A Mathematical Theory of Communication“ offiziell die „Informationstheorie“ vor und läutete damit eine neue Ära ein. Heute wird die Informationstheorie in vielen Bereichen breit eingesetzt, beispielsweise im maschinellen Lernen, im Deep Learning und in der Datenwissenschaft.

Wie wir alle wissen, ist der Turing Award die höchste Auszeichnung in der Computerbranche. Der Turing Award wurde 1966 von der Association for Computing Machinery ins Leben gerufen, um Turings herausragende Beiträge zu würdigen. Ebenso wichtig ist der Shannon Award im Bereich Information.

Der Unterschied besteht darin, dass Turing 1954 starb und nicht erfahren konnte, dass die Welt diesen Preis für ihn gestiftet hatte.

Shannon hatte viel mehr Glück. Der Shannon Award wurde verliehen von Die IEEE Society wurde 1972 gegründet, um Wissenschaftler und Ingenieure zu ehren, die herausragende Beiträge auf dem Gebiet der Informationstheorie geleistet haben. In der ersten Sitzung erhielt Shannon selbst den Shannon Award.

„Shannon hat den Shannon Award gewonnen und die Geschichte nennt es die Shannon-Routine.“