HyperAI超神经
首页资讯最新论文教程数据集百科SOTALLM 模型天梯GPU 天梯顶会
全站搜索
关于
HyperAI超神经

Gnnwr 时空智能回归 (STIR) 模型 Demo

在线运行此教程
PyPI - License

该教程为时空智能回归 (STIR) 模型的 PyTorch 实现，算力资源采用 RTX 4090，「工作空间」内含以下 notebook 自动化脚本演示示例：

  • GNNWR：演示示例为「PM2.5 空气污染」

英文版：demo_gnnwr.ipynb

中文版：demo_gnnwr-cn.ipynb

  • GTNNWR：演示示例为「近岸海域关键营养盐的时空分布」

英文版：demo_gnnwr.ipynb

中文版：demo_gnnwr-cn.ipynb

此外，本代码库包含：

  1. GNNWR 、 GTNNWR 模型及其他衍生模型的源代码
  2. 模型的教程笔记（notebook 自动化脚本）
  3. 已发布的 Python Wheels

目录

1. 简介

GNNWR (Geographically Neural Network Weighted Regression) 是由浙江大学 GIS 实验室于 2020 年开发的一种基于 PyTorch 的时空智能回归模型，专门用于处理空间和时间非平稳性问题。该模型通过将地理邻近性和非平稳权重的非线性拟合转化为神经网络的表示和构建，实现了对复杂地理过程的高精度建模。

时空非平稳性是大多数地理过程的固有属性，其估计是时空非平稳关系建模的关键问题。为了刻画时空非平稳关系，研究团队将地理邻近性的表达和非平稳权重的非线性拟合转化为神经网络的表示和构建，建立了一系列时空智能回归 (STIR) 模型，包括地理神经网络加权回归 (GNNWR) 和地理时间神经网络加权回归 (GTNNWR) 。

模型性能显著优于经典时空回归方法，例如地理加权回归 (GWR) 和地理时间加权回归 (GTWR)，以及神经网络和随机森林等机器学习方法。 STIR 模型已应用于生态环境建模、大气污染物估算、城市房价研究等领域。相关研究成果发表在「国际地理信息科学杂志」、「环境科学与技术」、「环境污染」、「整体环境科学」、「国际应用地球观测与地理信息杂志」等期刊上。

2. 模型

2.1 GNNWR

GNNWR（地理神经网络加权回归）是一种用于处理各种复杂地理过程领域中空间非平稳性的模型。本文提出了一种空间加权神经网络 (SWNN) 来表示非平稳权重矩阵，并通过加权最小二乘法对这些权重进行局部估计。 GNNWR 凭借其卓越的拟合能力，拥有结构良好的非平稳权重矩阵，从而能够更好地描述环境和城市研究中的复杂地理过程。

GNNWR

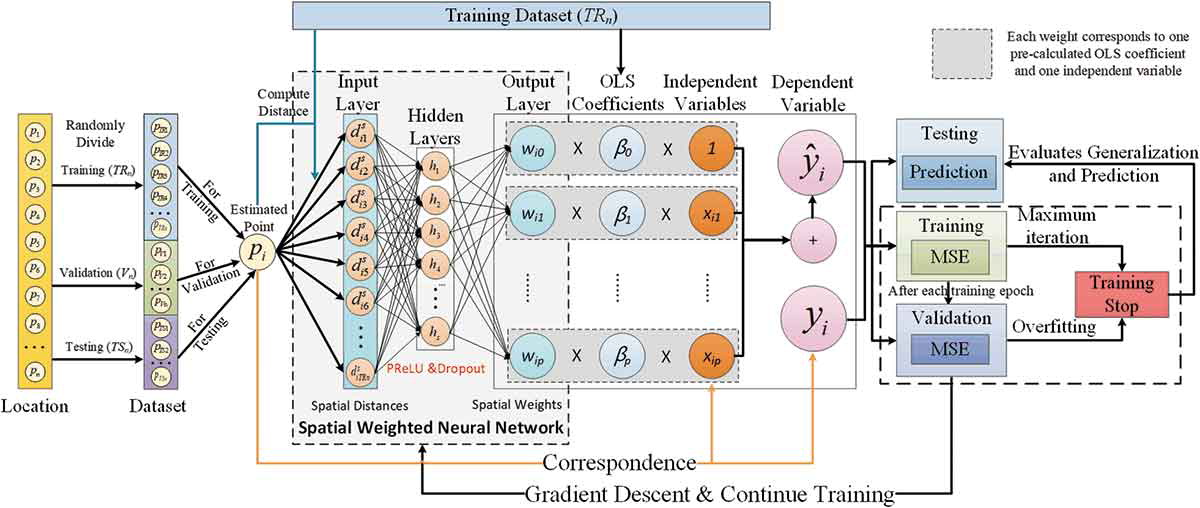
Du, Z., Wang, Z., Wu, S., Zhang, F., & Liu, R. (2020). Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. International Journal of Geographical Information Science, 34(7), 1353-1377.

演示示例-PM2.5 空气污染

英文版：demo_gnnwr.ipynb

中文版：demo_gnnwr-cn.ipynb

2.2 GTNNWR

GTNNWR（地理和时间神经网络加权回归），是一种估计时空非平稳关系的模型。由于时空非平稳性的存在，要素的空间关系随着时空结构的变化而表现出明显的差异性。时空距离的计算是解决时空非平稳问题的重要方面。因此，本模型将时空距离引入 GNNWR 模型，并提出时空邻近神经网络（STPNN）来精确计算时空距离，并与 GNNWR 模型中的 SWNN 协同计算时空非平稳权重矩阵，从而实现时空非平稳关系的精确建模。

GTNNWR

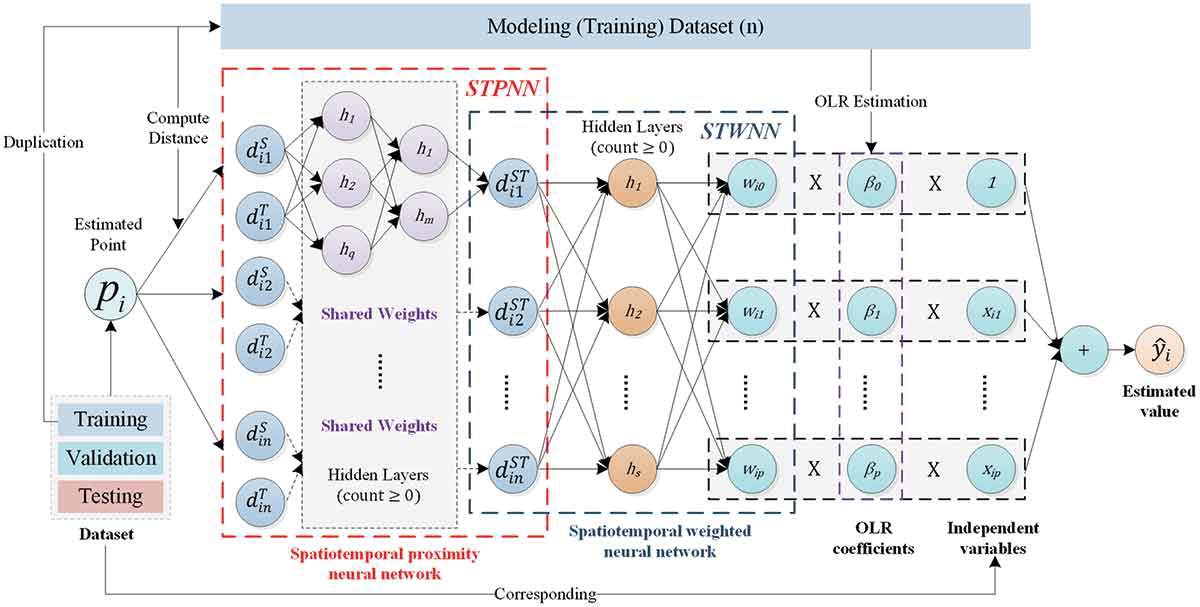
Wu, S., Wang, Z., Du, Z., Huang, B., Zhang, F., & Liu, R. (2021). Geographically and temporally neural network weighted regression for modeling spatiotemporal non-stationary relationships. International Journal of Geographical Information Science , 35(3), 582-608.

演示示例-近岸海域关键营养盐的时空分布

英文版：demo_gnnwr.ipynb

中文版：demo_gnnwr-cn.ipynb

3. 其他研究案例

3.1 大气环境

3.1.1 PM2.5 空气污染

空气污染，尤其是 PM2.5 的测量，近年来成为中国的热门研究课题。由于中国地形复杂、地域范围广，使用分散的 PM2.5 观测站数据，估算并绘制中国范围内的 PM2.5 浓度分布，面临着显著的空间非平稳性和复杂的非线性问题，难以实现高精度、高精细的分布估算。 GNNWR 模型能够结合气溶胶光学厚度 (AOD) 、数字高程模型 (DEM) 以及一些气候因子，获得中国范围内空间连续的 PM2.5 浓度估算值。与传统回归模型的结果相比，GNNWR 模型的 PM2.5 估算结果更接近地面观测值，在高值区精度更高，细节更丰富。

PM25

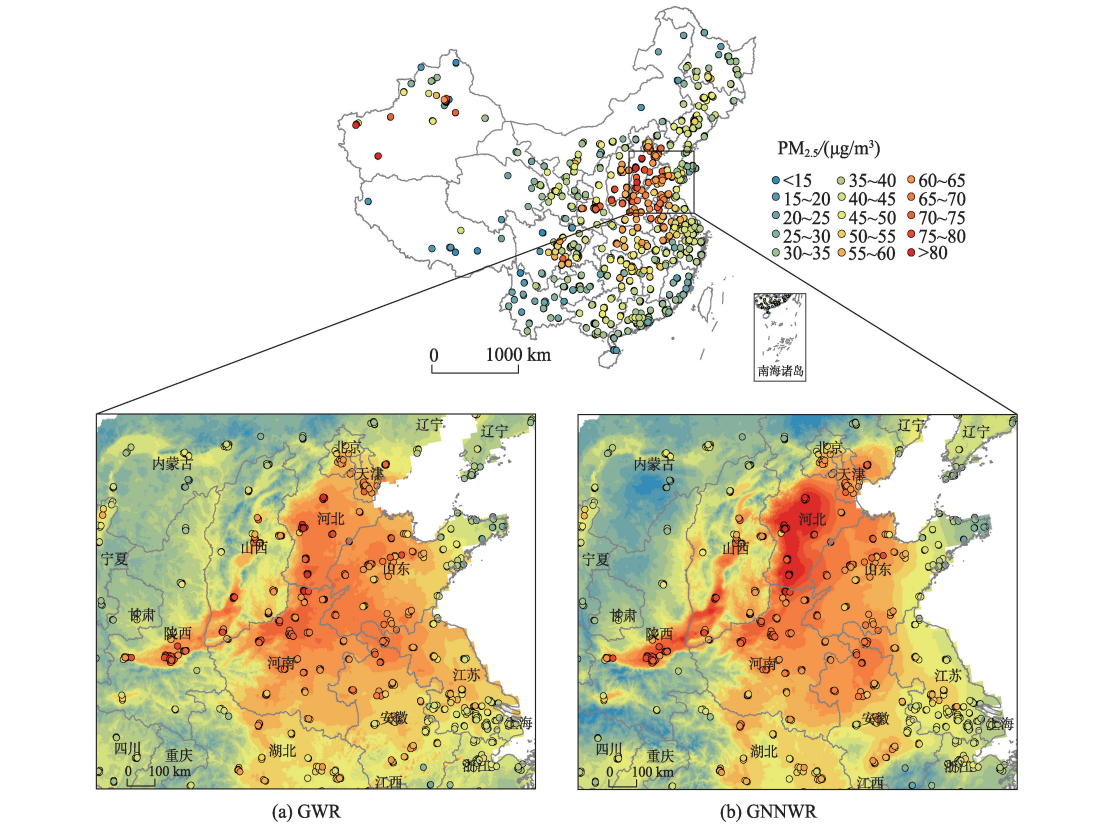
Chen, Y., Wu, S., Wang, Y., Zhang, F., Liu, R., & Du, Z. (2021). Satellite-based mapping of high-resolution ground-level pm2. 5 with VIIRS IP AOD in China through spatially neural network weighted regression. Remote Sensing, 13(10), 1979.

👉 Modeling PM2.5 with GNNWR on Deep-time.org

3.1.2 NO2 大气污染

本研究利用 TROPOMI 遥感数据、地面观测数据及其他辅助数据，基于 GTNNWR 模型构建了京津冀地区地面 NO2 浓度的高分辨率时空分布特征并进行评估。结果表明，GTNNWR 模型在性能指标上优于随机森林 (RF) 和卷积神经网络 (CNN) 模型，在考虑时空非平稳性时表现出更高的可靠性。本研究为京津冀地区大气环境管理和污染防治提供了重要的数据支持和参考。

NO2

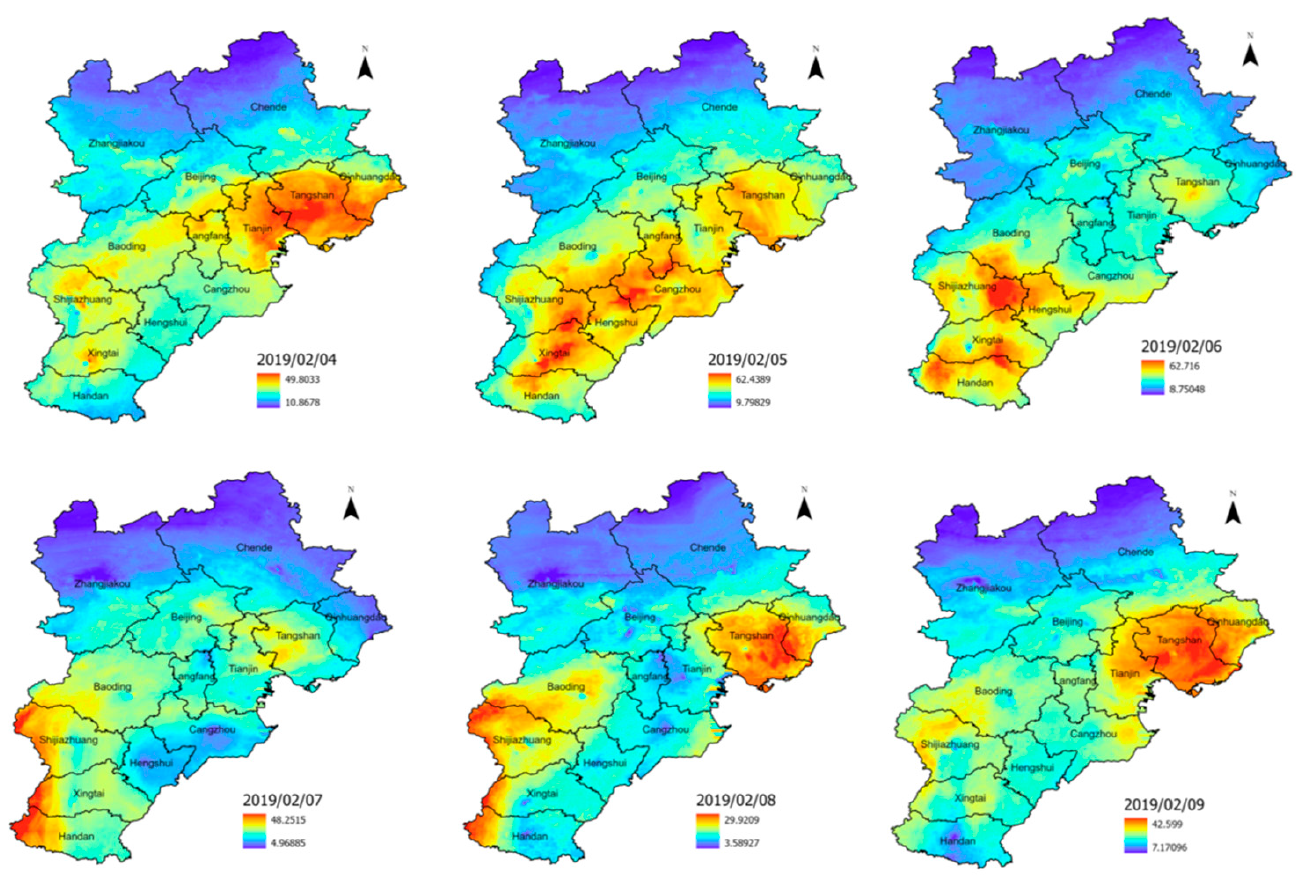
Liu, C., Wu, S., Dai, Z., Wang, Y., Du, Z., Liu, X., & Qiu, C. (2023). High-Resolution Daily Spatiotemporal Distribution and Evaluation of Ground-Level Nitrogen Dioxide Concentration in the Beijing–Tianjin–Hebei Region Based on TROPOMI Data. Remote Sensing, 15(15), 3878.

3.2 海岸带与海洋环境

3.2.1 水质

由于遥感与现场数据整合过程中涉及空间非平稳性和复杂的非线性，对大规模复杂海岸带水域进行准确评估是一项巨大的挑战。为了应对这一挑战，我们基于新提出的 GNNWR 模型，开发了一种水质评估方法，并基于中国水质分类标准综合指数，获得了高精度、符合实际的水质分布。与广泛使用的模型相比，GNNWR 模型具有更高的预测性能（平均 R² = 84%），并且获得的 2015-2017 年 5 月和 2015 年 8 月的水质分类（WQC）图能够直观、合理地描绘出零污染区水质的时空格局。

WaterQuality

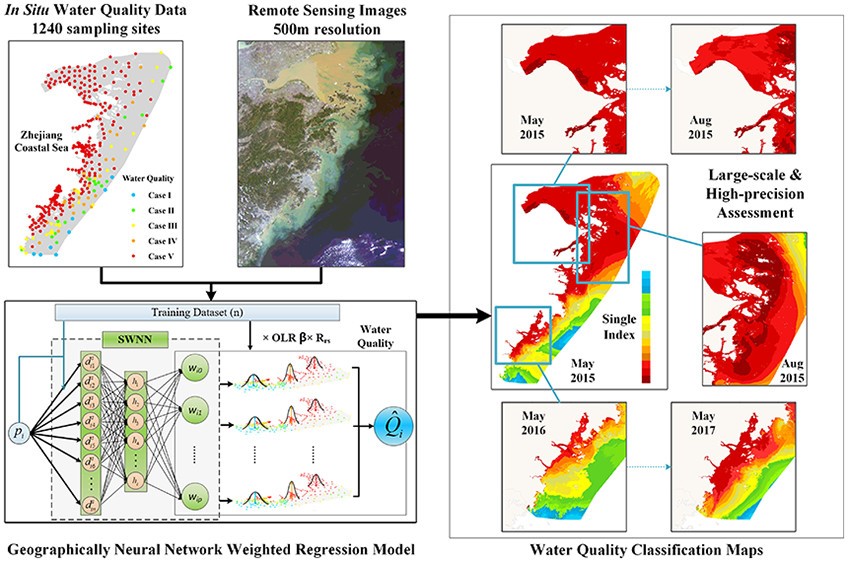
Du, Z., Qi, J., Wu, S., Zhang, F., & Liu, R. (2021). A spatially weighted neural network based water quality assessment method for large-scale coastal areas. Environmental science & technology, 55(4), 2553-2563.

3.2.2 海岸带环境

溶解硅酸盐 (DSi) 从陆地向海岸带环境的迁移对全球生物地球化学循环至关重要。然而，由于时空变异性、非线性建模和较低的采样分辨率，精确定位海岸带 DSi 的分布十分复杂。 GTNNWR 模型通过将稀疏采样点和未知点之间的时空关系转化为时空距离和权重，并利用神经网络确定非线性距离和非平稳权重，在拟合精度和泛化能力方面均优于传统的回归模型。这种有效的基于数据驱动的方法有助于探索海岸带海域（例如表层 DSi）的细尺度动态变化。

DSI

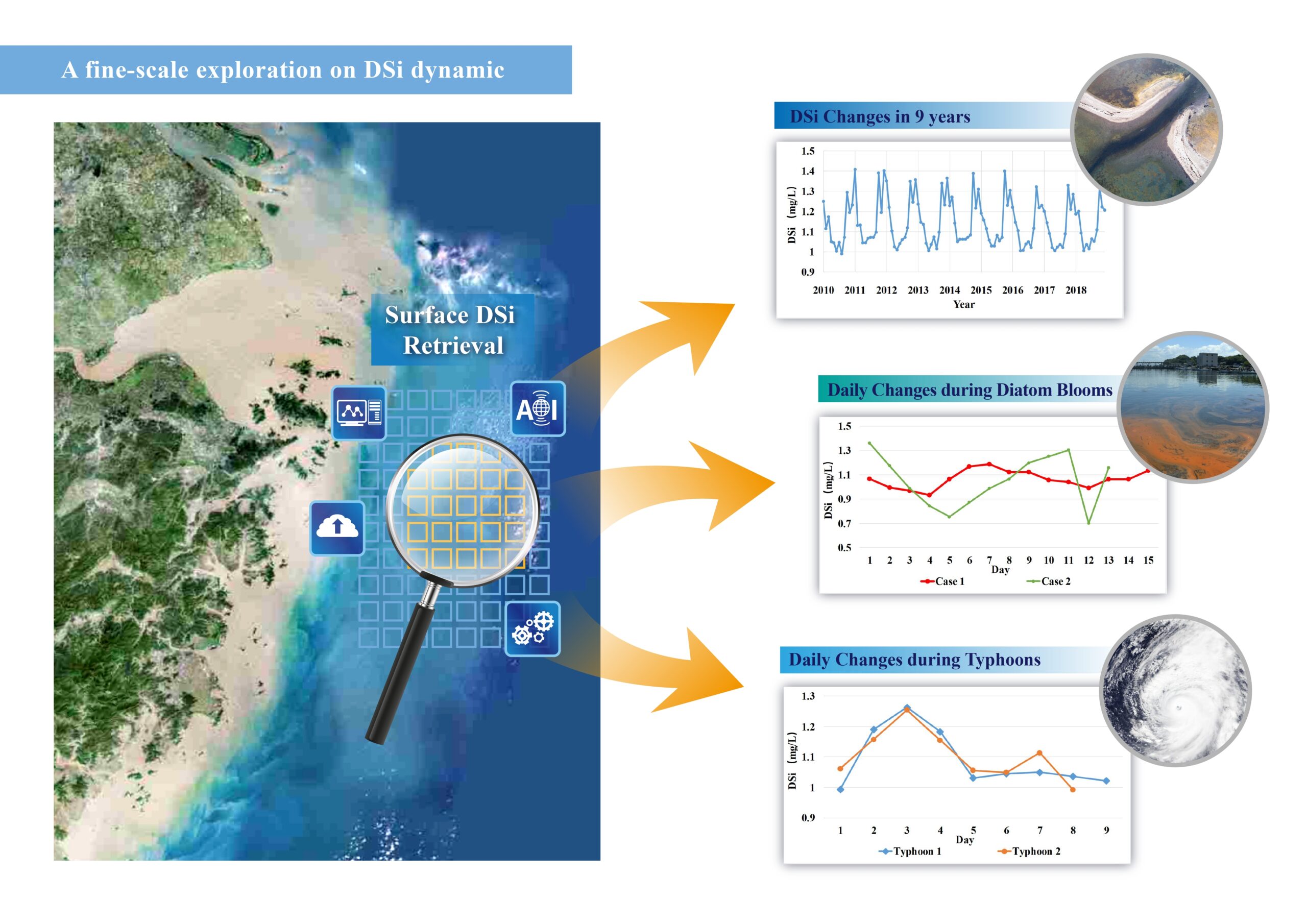
Qi, J., Du, Z., Wu, S., Chen, Y., & Wang, Y. (2023). A spatiotemporally weighted intelligent method for exploring fine-scale distributions of surface dissolved silicate in coastal seas. Science of The Total Environment , 886, 163981.

👉 Modeling DSi with GTNNWR on Deep-time.org

3.2.3 表层海水 pCO2

北太平洋是重要的碳汇，但由于其规模巨大且影响复杂，其时空动态仍缺乏深入研究。现有的机器学习模型缺乏可解释性，限制了对潜在机制的洞察。为了解决这个问题，我们引入了网格化时空神经网络加权回归 (GSTNNWR) 模型，该模型能够准确预测表层 pCO2，同时量化环境影响。

Liu, Y., Chen, Y., Huang, Z., Liang, H., Qi, J., Wu, S., & Du, Z. (2024). Spatiotemporal weighted neural network reveals surface seawater pCO2 distributions and underlying environmental mechanisms in the North Pacific Ocean. International Journal of Applied Earth Observation and Geoinformation, 133, 104120.

3.3 城市

3.3.1 房价

房价与城镇新居民的生活息息相关，也是政府需要密切关注的重要经济指标。与传统回归模型相比，GNNWR 和 GTNNWR 模型能够借助神经网络提高房地产估价的准确性，是评估房价的实用且有效的方法。

GNNWR 模型集成了一种优化的空间邻近度量。优化的空间邻近度量融合了多种距离度量，提高了其对空间非平稳过程的建模能力。

OSP

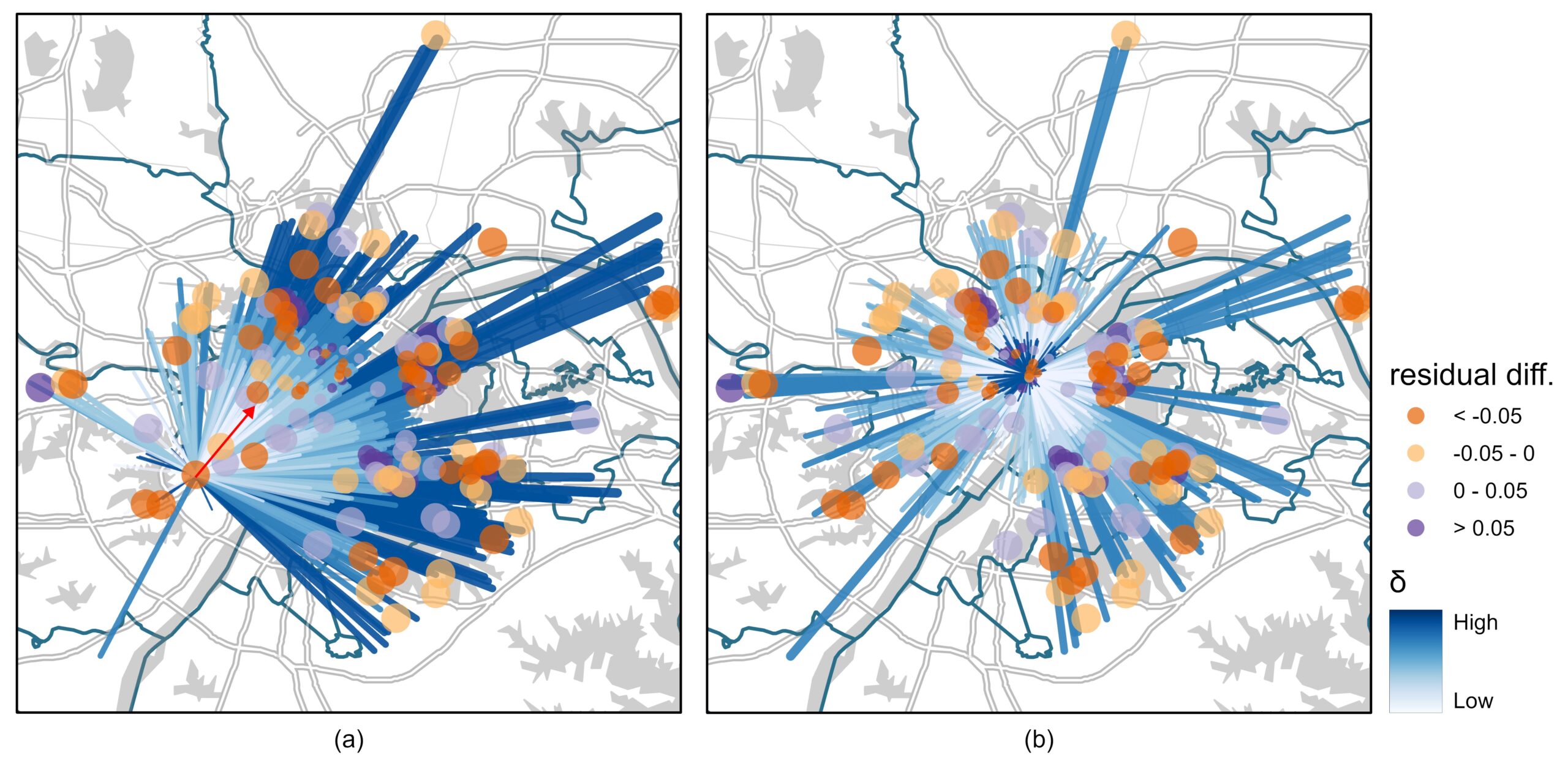
Ding, J., Cen, W., Wu, S., Chen, Y., Qi, J., Huang, B., & Du, Z. (2024). A neural network model to optimize the measure of spatial proximity in geographically weighted regression approach: a case study on house price in Wuhan. International Journal of Geographical Information Science, 1–21.

通过使用基于注意力的架构将上下文相似性纳入空间非平稳性估计，房价可以更好地适应复杂的城市区域。

CatGWR

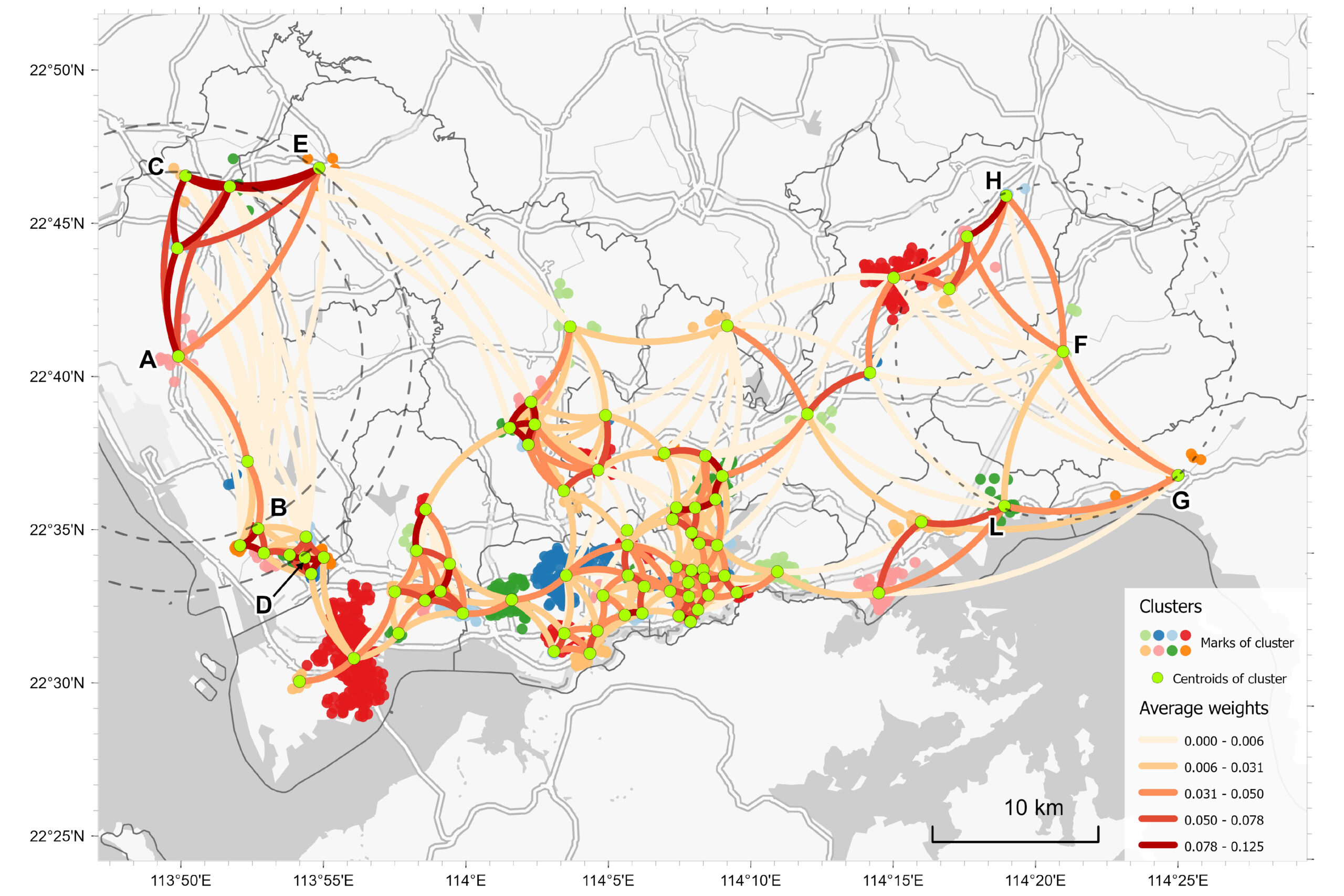
Wu, S., Ding, J., Wang, R., Wang, Y., Yin, Z., Huang, B., & Du, Z. (2025). Using an attention-based architecture to incorporate context similarity into spatial non-stationarity estimation. International Journal of Geographical Information Science, 1–24

HousePrice

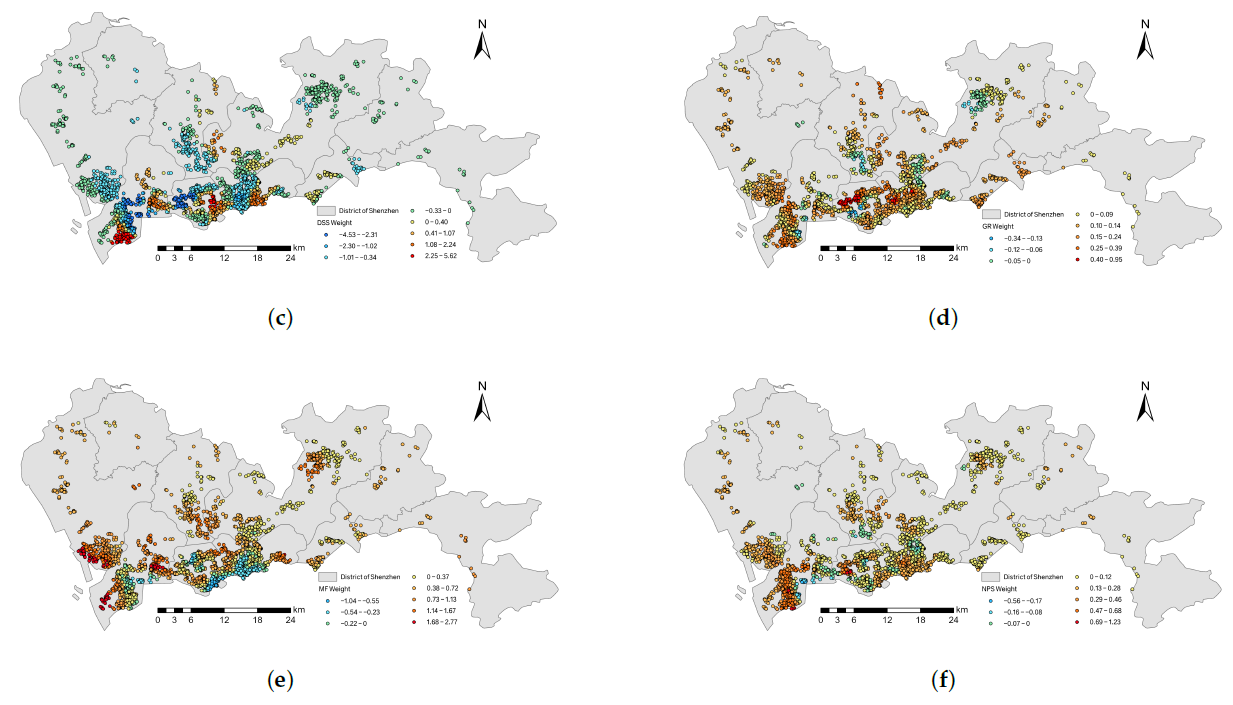
Wang, Z., Wang, Y., Wu, S., & Du, Z. (2022). House Price Valuation Model Based on Geographically Neural Network Weighted Regression: The Case Study of Shenzhen, China. ISPRS International Journal of Geo-Information, 11(8), 450.

3.3.2 地表温度与夜间光

空间降尺度是获取高分辨率地表温度（LST）数据用于热环境研究的重要方法。为了有效解决地表温度降尺度问题，本文提出了一种基于 GNNWR 的高分辨率地表温度降尺度方法。结果表明，在四个地形、地貌和季节差异较大的试验区，与广泛使用的方法相比，所提出的 GNNWR 模型获得了更高的降尺度精度。鉴于 GNNWR 的高精度和模型性能，研究结果表明，GNNWR 是一种实用的地表温度降尺度方法。

LST

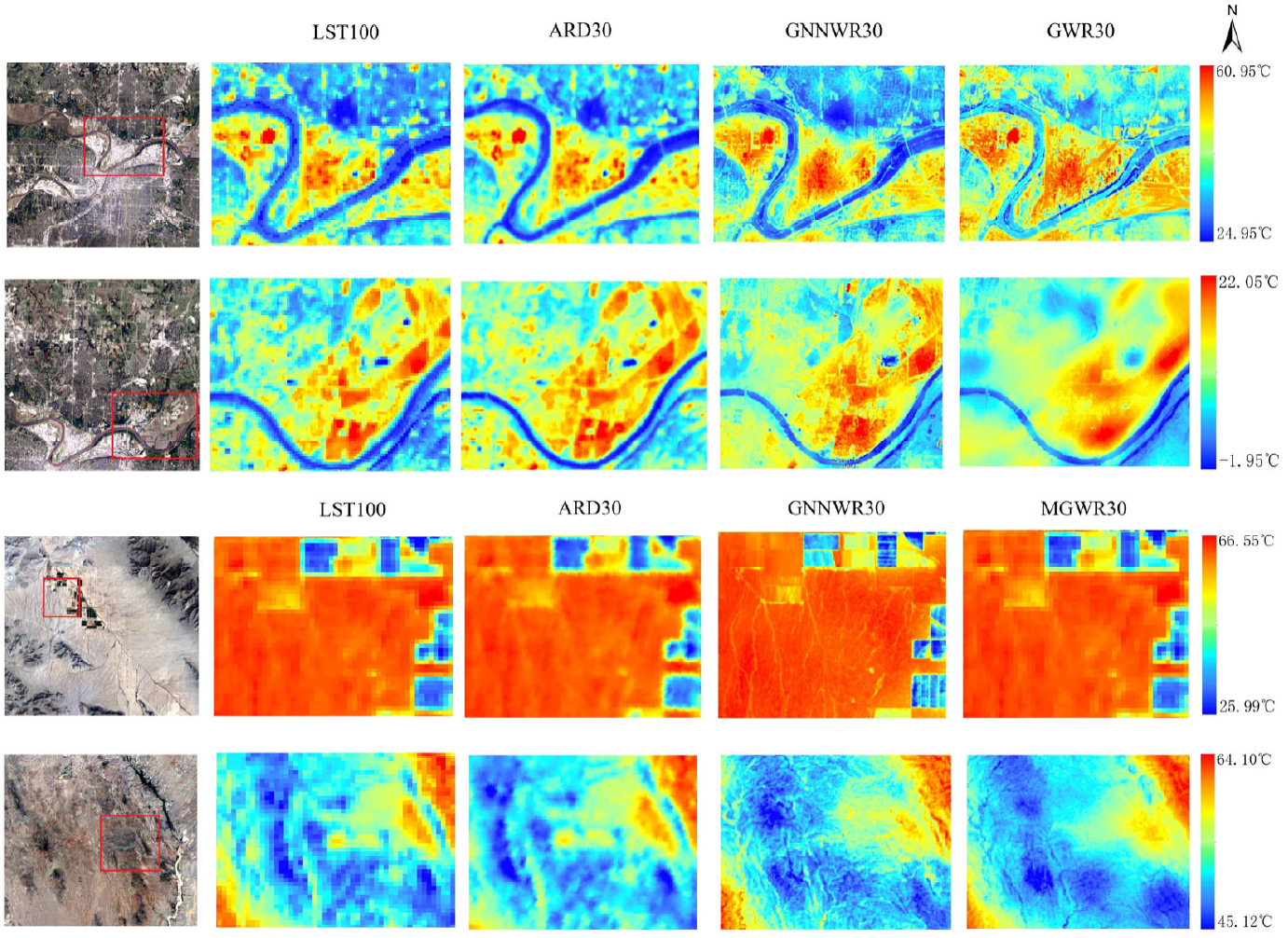
Liang, M., Zhang, L., Wu, S., Zhu, Y., Dai, Z., Wang, Y., … & Du, Z. (2023). A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression. Remote Sensing, 15(7), 1740.

利用卫星影像降尺度分析夜间灯光 (NTL) 对城市扩张和社会经济研究至关重要，但由于地理复杂性和因素不确定性，其面临诸多挑战。为了解决这一问题，我们提出了多因素地理神经网络加权回归 (MF-GNNWR) 框架，该框架整合了地表、社会经济和人类活动因素，以提升异质性城市区域的夜间灯光 (NTL) 精度。

Zhang, L., Wu, S., Liang, M., Jing, H., Shi, S., Zhu, Y., … & Du, Z. (2024). A Downscaling Framework for Urban Nighttime Light Based on Multi-Factor Geographically Neural Network Weighted Regression. IEEE Transactions on Geoscience and Remote Sensing.

3.4 地质学

3.4.1 矿产勘探潜力

在矿产预测领域，准确预测矿产资源对于满足现代社会的能源需求至关重要。地理神经网络加权逻辑回归用于矿产勘探地图绘制。该模型将空间模式、神经网络与 Shapley 的加性解释理论相结合，有效地处理变量的各向异性和变量之间的非线性关系，从而实现准确预测，并对复杂空间环境下的成矿作用提供解释。

mineral prospectivity

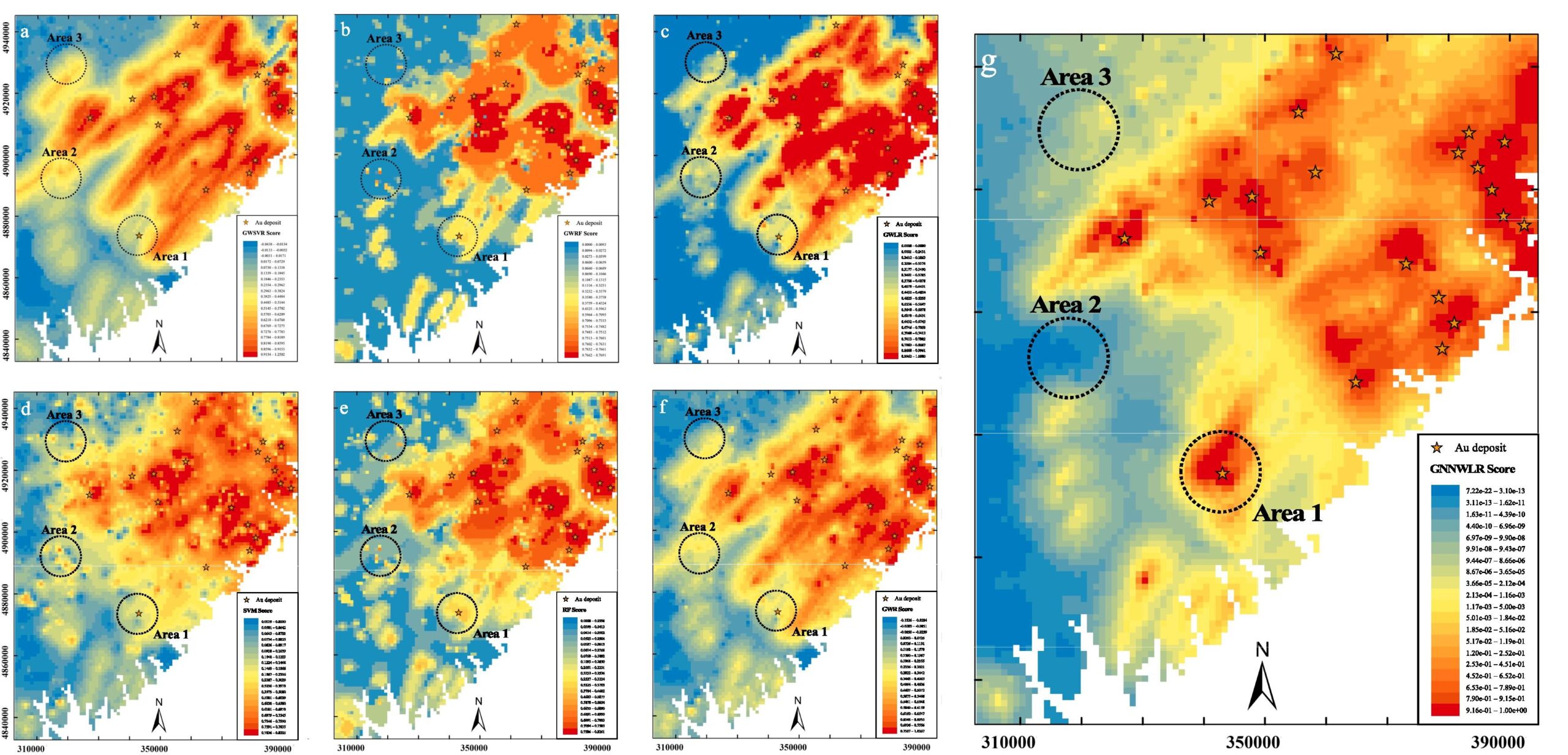
Wang, L., Yang, J., Wu, S., Hu, L., Ge, Y., & Du, Z. (2024). Enhancing mineral prospectivity mapping with geospatial artificial intelligence: A geographically neural network-weighted logistic regression approach. International Journal of Applied Earth Observation and Geoinformation, 128, 103746.

3.4.2 热流

地表热流 (SHF) 对于理解地球内部动力学至关重要。青藏高原是全球气候和地球动力学研究的关键区域，但由于观测数据稀疏，缺乏全面的 SHF 数据。为了解决这一问题，我们开发了增强可解释性的地理神经网络加权回归模型 (EI-GNNWR)，该模型整合了空间异质性和非线性地球物理相互作用。我们的模型准确地预测了整个高原的 SHF，揭示了受莫霍面深度、山脊和地形影响，SHF 高值集中在南部、东北部和东南部。这些发现增强了对该区域地热过程和构造活动的理解。

SHF

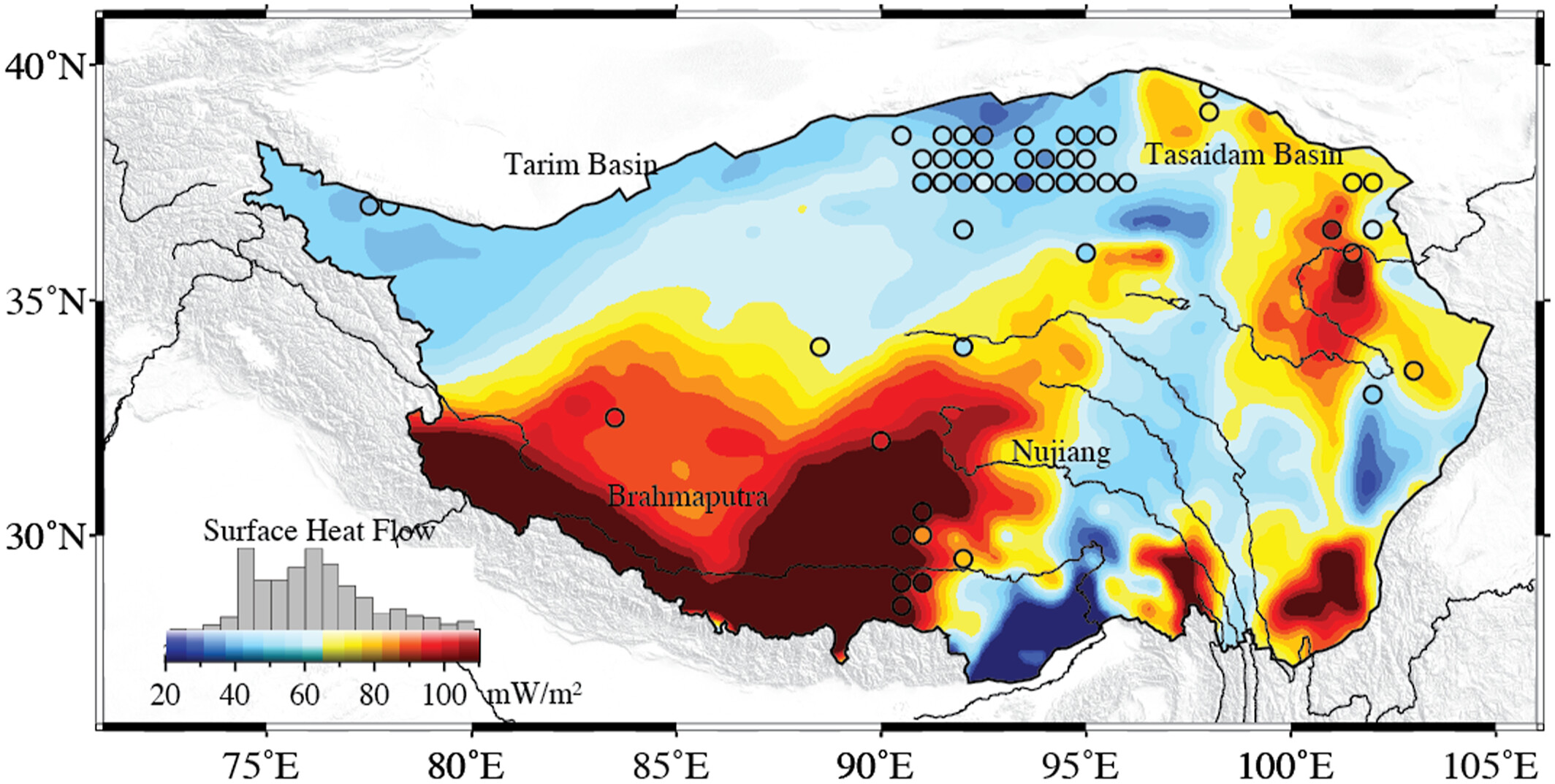
Zhang, Z., Wu, S., Zhang, B., Du, Z., & Xia, Q. (2024). The distribution of surface heat flow on the Tibetan Plateau revealed by data‐driven methods. Journal of Geophysical Research: Solid Earth, 129(10), e2023JB028491.

!! 此外，这些时空智能回归模型可以应用于其他时空建模问题和社会经济现象。

4. 相关研究论文

4.1 算法

  1. Du, Z., Wang, Z., Wu, S., Zhang, F., & Liu, R. (2020). Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. International Journal of Geographical Information Science, 34(7), 1353-1377.
  2. Wu, S., Wang, Z., Du, Z., Huang, B., Zhang, F., & Liu, R. (2021). Geographically and temporally neural network weighted regression for modeling spatiotemporal non-stationary relationships. International Journal of Geographical Information Science , 35(3), 582-608.
  3. Dai, Z., Wu, S., Wang, Y., Zhou, H., Zhang, F., Huang, B., & Du, Z. (2022). Geographically convolutional neural network weighted regression: A method for modeling spatially non-stationary relationships based on a global spatial proximity grid. International Journal of Geographical Information Science, 36(11), 2248-2269.

4.2 案例研究演示

  1. Chen, Y., Wu, S., Wang, Y., Zhang, F., Liu, R., & Du, Z. (2021). Satellite-based mapping of high-resolution ground-level pm2. 5 with VIIRS IP AOD in China through spatially neural network weighted regression. Remote Sensing, 13(10), 1979.
  2. Qi, J., Du, Z., Wu, S., Chen, Y., & Wang, Y. (2023). A spatiotemporally weighted intelligent method for exploring fine-scale distributions of surface dissolved silicate in coastal seas. Science of The Total Environment , 886, 163981.
  3. Du, Z., Qi, J., Wu, S., Zhang, F., & Liu, R. (2021). A spatially weighted neural network based water quality assessment method for large-scale coastal areas. Environmental science & technology, 55(4), 2553-2563.
  4. Liang, M., Zhang, L., Wu, S., Zhu, Y., Dai, Z., Wang, Y., … & Du, Z. (2023). A High-Resolution Land Surface Temperature Downscaling Method Based on Geographically Weighted Neural Network Regression. Remote Sensing, 15(7), 1740.
  5. Liu, C., Wu, S., Dai, Z., Wang, Y., Du, Z., Liu, X., & Qiu, C. (2023). High-Resolution Daily Spatiotemporal Distribution and Evaluation of Ground-Level Nitrogen Dioxide Concentration in the Beijing–Tianjin–Hebei Region Based on TROPOMI Data. Remote Sensing, 15(15), 3878.
  6. Wang, Z., Wang, Y., Wu, S., & Du, Z. (2022). House Price Valuation Model Based on Geographically Neural Network Weighted Regression: The Case Study of Shenzhen, China. ISPRS International Journal of Geo-Information, 11(8), 450.
  7. Wu, S., Du, Z., Wang, Y., Lin, T., Zhang, F., & Liu, R. (2020). Modeling spatially anisotropic nonstationary processes in coastal environments based on a directional geographically neural network weighted regression. Science of the Total Environment, 709, 136097.
  8. Wang, L., Yang, J., Wu, S., Hu, L., Ge, Y., & Du, Z. (2024). Enhancing mineral prospectivity mapping with geospatial artificial intelligence: A geographically neural network-weighted logistic regression approach. International Journal of Applied Earth Observation and Geoinformation, 128, 103746.
  9. Ding, J., Cen, W., Wu, S., Chen, Y., Qi, J., Huang, B., & Du, Z. (2024). A neural network model to optimize the measure of spatial proximity in geographically weighted regression approach: a case study on house price in Wuhan. International Journal of Geographical Information Science, 1–21.

5. Group

Leaders

Zhenhong DuZhenhong DuPh.DProfessor/ Ph.D SupervisorThe National Science Fund for Distinguished Young ScholarsDean of the School of Earth sciencesZhejiang University
Sensen WuSensen WuPh.DProfessor/ Ph.D SupervisorZhejiang University

Members

  • Jin Qi, Postdoctoral fellow, Zhejiang University
  • Jiale Ding, PhD student, Zhejiang University
  • Yi Liu, Undergraduate student, Zhejiang University
  • Ziyu Yin, Undergraduate student, Zhejiang University

6. License

GPLv3 license

引用信息:

Du, Z., Wang, Z., Wu, S., Zhang, F., & Liu, R. (2020). Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. International Journal of Geographical Information Science, 34(7), 1353-1377.

Wu, S., Wang, Z., Du, Z., Huang, B., Zhang, F., & Liu, R. (2021). Geographically and temporally neural network weighted regression for modeling spatiotemporal non-stationary relationships. International Journal of Geographical Information Science , 35(3), 582-608.

Yin, Z., Ding, J., Liu, Y., Wang, R., Wang, Y., Chen, Y., Qi, J., Wu, S., and Du, Z. (2024). GNNWR: an open-source package of spatiotemporal intelligent regression methods for modeling spatial and temporal nonstationarity. Geoscientific Model Development, 17 (22), 8455–8468.