Command Palette
Search for a command to run...
精准预测武汉房价!浙大 GIS 实验室提出 Osp-gnnwr 模型:准确描述复杂空间过程和地理现象

住房是人类福祉和社会发展的重要组成部分,住房价格波动受到社会的广泛关注。中国是一个地域跨度极广的国家,即使是在同一个城市的同一管辖区,不同区域的房屋由于社区环境、学区、配套商业等因素的不同,都会导致房价存在差异,因而房价问题研究关注的热点之一是其空间分异及影响机制,也就是所谓的「空间异质性」。
近年来,房价空间差异日益显著,单一的距离度量方式在捕捉复杂地理环境中房价的「空间异质性」时,显得捉襟见肘。尤其在武汉市这样的大城市中,自然地貌(如河流、湖泊)以及城市基础建设(如桥梁、隧道、多层道路网络)等因素对房价的影响错综复杂,传统地理加权回归模型 (GWR) 在衡量空间邻近性时面临挑战。
在此背景下,来自浙江大学 GIS 实验室的研究人员在地理信息科学领域知名期刊 International Journal of Geographical Information Science 上发表了题为「A neural network model to optimize the measure of spatial proximity in geographically weighted regression approach: a case study on house price in Wuhan」的研究论文。
本研究创新性地引入神经网络方法对观测点间的多种空间邻近性度量 (如欧式距离、旅行时间等) 进行非线性耦合,得到优化的空间邻近性度量 (OSP),从而提升模型对房价预测的准确性。
为解决抽象的「空间邻近性」无法构造损失函数、神经网络难以训练的问题,本研究将 OSP 与地理神经网络加权回归方法 (Geographically Neural Network Weighted Regression, GNNWR) 进一步结合,构建了 osp-GNNWR 模型,通过解算因变量与自变量的空间非平稳回归关系实现神经网络的训练。
研究亮点:
- 通过引入优化的空间邻近度指标,并将其融入神经网络架构,有效地改善了地理加权回归在房价等地理过程的空间分布研究中的适用性
- 通过模拟数据集和武汉市房价实证案例的研究,论文提出的模型被证明具有更好的全局性能,能更准确地描述复杂的空间过程和地理现象
- 为研究如何因地制宜地定制空间邻近度度量标准,进而提升各类地理空间回归模型的表现,开辟了新途径

论文地址:
https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2343771
开源项目「awesome-ai4s」汇集了百余篇 AI4S 论文解读,还提供海量数据集与工具:
https://github.com/hyperai/awesome-ai4s
数据集:以武汉作为典型研究区域
模拟数据集
为了评估 osp-GNNWR 模型的拟合精度,研究人员生成了一个 64×64 的空间异质性模拟数据集。模拟数据集的空间异质性不仅体现在直线距离上,也表现出由非欧式距离定义的空间分布特征,能够展示 OSP 的有效性。
实际数据集
湖北省省会武汉市位于中国中部,坐落在汉江汇入长江的交汇点上。武汉气候湿润,属于亚热带气候,降雨充沛,拥有众多河流、湖泊和池塘,这些特点使得评估空间临近性变得具有挑战性。作为中国中部最大、人口最密集的城市,武汉同时还拥有繁荣的房地产市场,为构建一种针对武汉特定房地产动态的综合模型提供了充足的数据。
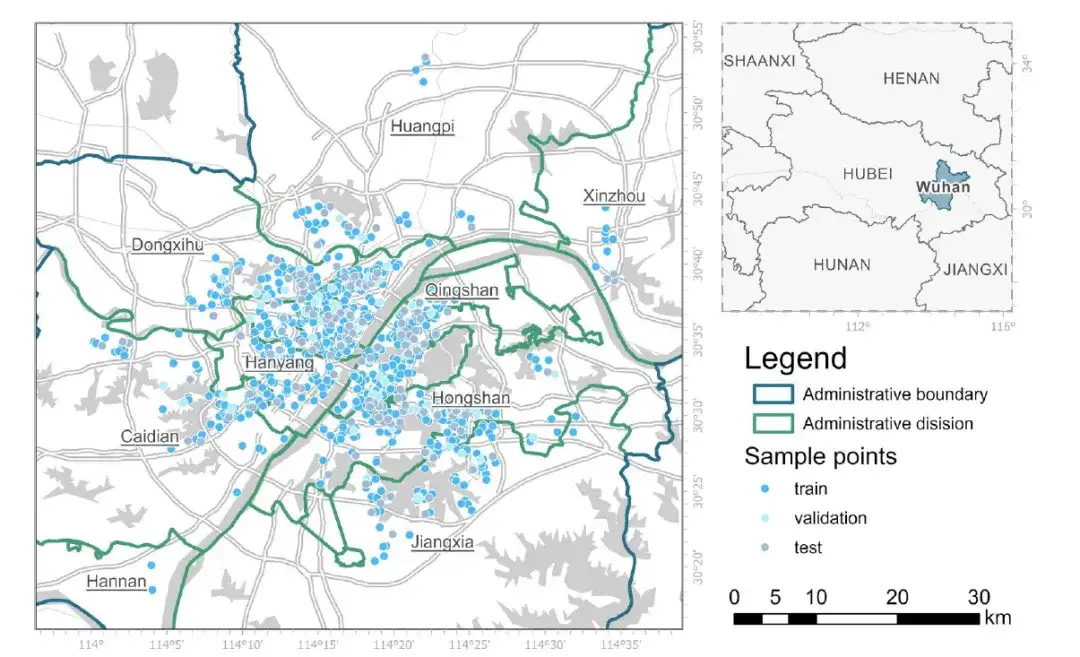
为此,研究人员汇编了一份包含 968 个不同房地产样本的数据集,这些数据来自于 2019 年在武汉范围内的二手住宅交易记录,数据来源为安居客(https://wuhan.anjuke.com)。所有这些记录都经过了清洗,特殊的房产类型(如别墅)被排除在外,并且数据质量得到了保证。
模型架构:引入优化的空间邻近度指标并将其融入神经网络
osp-GNNWR 模型的构建分为两步:
第一步:获得优化的空间邻近性度量 (OSP)
为了在复杂的地理分析中获得更准确的空间邻近度测量,本研究整合了多种距离测量方法,包括欧式距离、曼哈顿距离和旅行时间等,以优化空间邻近度 (OSP) 。通过这种方式,优化的空间邻近度测量可以更好地反映复杂空间关系中的各种影响因素,从而提高空间回归模型的拟合度和解释力。
第二步:将 OSP 与 GNNWR 进一步结合,研究人员提出了 osp-GNNWR 模型,如下图所示:
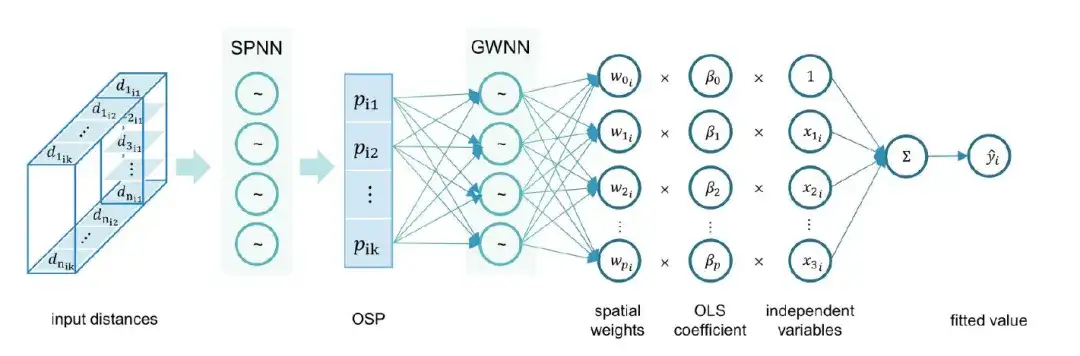
具体而言,osp-GNNWR 模型的训练和验证程序如下:
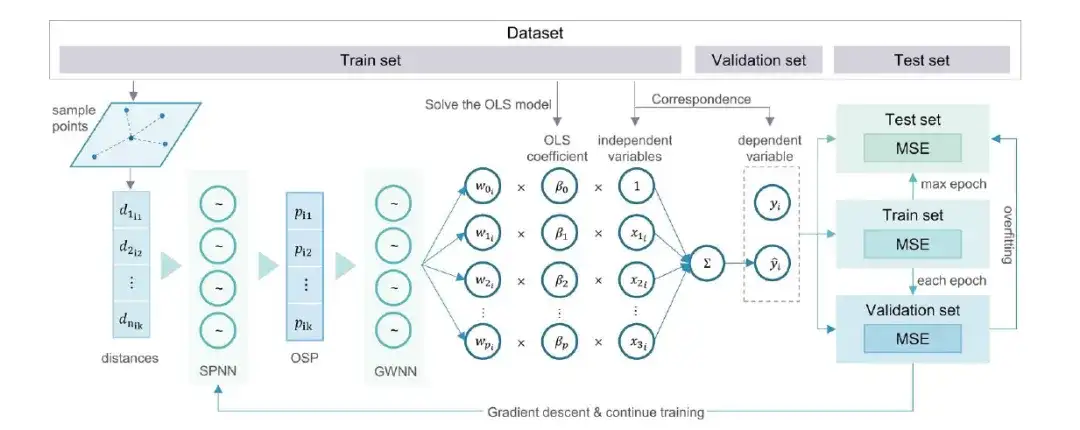
步骤 1:提取用于构建回归模型的因变量 (dependent variables) 和自变量 (independent variables);
步骤 2:将数据集按适当比例随机划分为训练集 (Train set) 、验证集 (Validation set) 和测试集 (Test set);
步骤 3:在 osp-GNNWR 模型中计算样本距离 (sample distances) 作为空间信息;
步骤 4:利用输入变量 (input variables) 和空间信息,建立包含网络结构和超参数的 osp-GNNWR 模型;
步骤 5:从训练集中获取 mini-batch 数据,使用梯度下降算法 (gradient descent algorithm) 进行训练,并评估拟合优度,如使用均方误差 (MSE) 作为损失函数;
步骤 6:评估当前周期 (epoch) 是否完成;如果未完成,返回步骤 5 。
步骤 7:在验证集上评估损失函数,以确定是否存在过拟合;如果损失比先前的最优结果有所改善,则保留新的优越模型;否则,增加过拟合容忍度的计数;
步骤 8:评估是否达到过拟合容忍度或周期数的最大值 (max epoch);达到限制时,训练停止,使用测试集评估最新的优越模型;否则,从步骤 5 开始继续迭代。
通过上述步骤,研究人员可以有效训练并验证 osp-GNNWR 模型,以捕捉和解释复杂空间关系中的异质性,提高模型的准确性和可靠性。
研究结果:osp-GNNWR 模型具有更好的全局性能
首先来看基于模拟数据集进行分析的结果。在一组基于欧式距离和 Z-order 距离的模拟数据集上,研究人员采用了包括 OLS 、 GWR 、 GNNWR 和 osp-GNNWR 在内的模型进行对比,结果如下表所示:
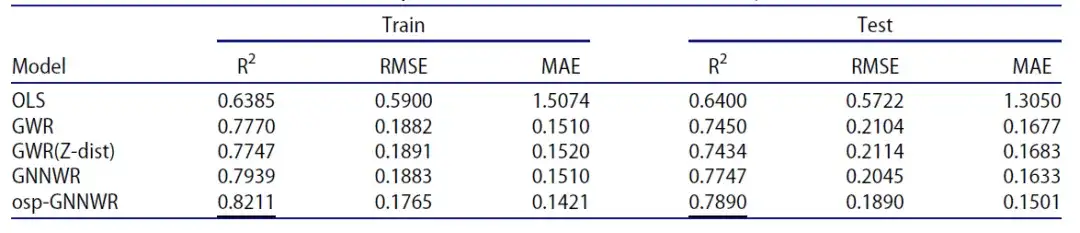
- R²:用于衡量一个变量(因变量)的变化中,有多少可以由另一个或多个变量(自变量)的变化来解释。这个值通常用于线性回归分析,以评估模型的拟合优度。 0% 表示模型无法解释响应变量在其均值附近的任何变异,即模型与数据之间几乎没有关系;100% 表示模型可以解释响应变量在其均值附近的所有变异,即模型完美地拟合了数据。
- RMSE(均方根差):用来衡量观测值与真值之间的偏差,数值越小表示模型的预测精度越高。
- MSE(平均绝对误差):用于衡量模型预测值与实际值之间的平均绝对偏差,数值越小表示模型的预测精度越高。
无论是在训练数据集还是测试数据集上,osp-GNNWR 模型都具有较高的 R²、较低的 RMSE 值和较低的 MSE 值,因此表现出更优的性能。这些模拟实验结果证明,osp-GNNWR 模型中使用的 SPNN 网络在处理输入距离时,具有出色的泛化能力和高度精确的拟合效果。因此,相比仅依赖欧氏距离的传统方法,osp-GNNWR 模型在描绘现实世界地理过程中的空间异质性方面具有潜在的优势。
其次是 osp-GNNWR 模型基于实际武汉市房价数据上的表现。下表显示了 OLS 、 GWR 、 GNNWR 和 osp-GNNWR 模型的性能比较结果:
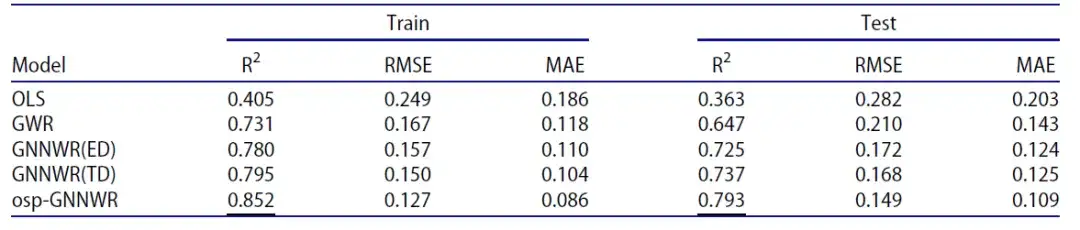
同样,无论是在训练数据集还是测试数据集上,osp-GNNWR 模型都具有较高的 R²、较低的 RMSE 值和较低的 MSE 值,因此展现出更优的性能。
值得注意的是,与 GNNWR(TD) 相比,osp-GNNWR 模型将测试数据集的 R² 从 0.737 提高到了 0.793,并且 RMSE 从 0.168 降低到了 0.149,MAE 从 0.125 降低到了 0.109 。这些结果表明,集成 OSP 提高了 osp-GNNWR 模型的拟合和预测性能,使其成为研究的模型中最有效的方法。
- GNNWR(TD):使用旅行时间作为临近性度量的 GNNWR 模型。
具体来看,在江夏区汤逊湖西岸、蔡甸区后宫湖沿岸以及汉江与长江交汇处等拥有复杂自然景观和基础设施的区域,洪山区和新洲区等高速公路网络发达、实际空间邻近性与物理距离差异较大的新兴开发区等区域,osp-GNNWR 模型残差显著小于其他模型,表现出更高的预测准确度。
总的来说,本研究的发现突显了 OSP 在增强 osp-GNNWR 模型表征空间异质性能力方面的有效性,从而推动了房地产市场内复杂空间关系的建模。
深度学习助力复杂的房价预测难题
探究住宅价格空间分异原因及影响机制,对维护房地产市场稳定发展,以及提升城市规划和居住满意度有着重要意义。然而,房价预测是一个十分复杂的问题,涉及到众多因素,如地理位置、交通便利性、学区、房龄、房屋类型等等。传统的方法通常基于统计学和机器学习,但是随着数据规模的增加和复杂性的提高,这些方法难以应对。深度学习具有强大的特征学习和分类能力,可以更好地处理这类问题。
为了提高房价预测的准确度,业内的研究主要从以下几个方向展开:
其一是混合模型方法,即结合深度学习和传统机器学习方法,发挥各自的优势。例如,可以将深度学习和支持向量机 (SVM) 或随机森林 (Random Forest) 等传统机器学习方法相结合,构建一个混合模型来进行房价预测。
其二是考虑时间序列数据,也就是在房价预测中,除了考虑房屋的静态属性外,还可以考虑时间序列数据,如历史房价、经济指标等,运用循环神经网络 (RNN) 等方法进行分析和预测。
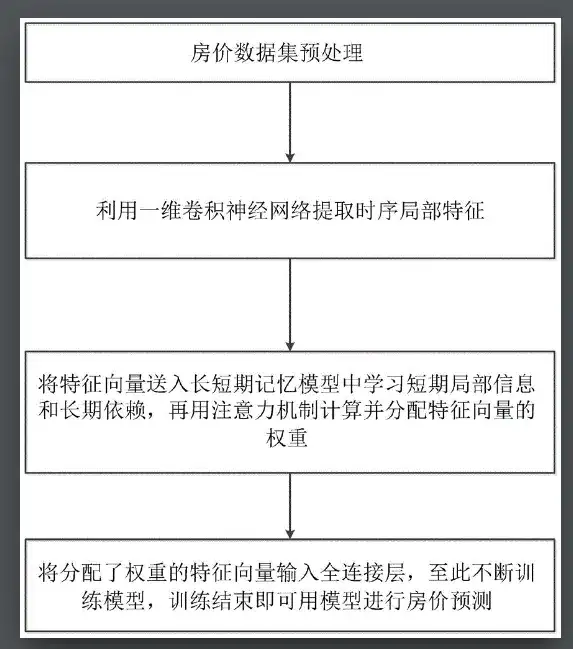
例如,有研究人员在 Google patents 上介绍了一种基于注意力机制的卷积时序房价预测方法。研究人员首先对房价数据集进行预处理,并得到由房屋价格相关多维因素按时间构成的序列。
考虑到影响房子价格有多维相关因素,对房屋价格趋势的波动和影响,使基于注意力机制的用卷积时序神经网络来对房价进行预测,其中采用了一维卷积神经网络对多维相关因素的特征进行处理,得到进一步特征提取和降维后的多维特征向量,再将特征向量输入到长短期记忆模型中学习特征之间的长期整体趋势和短期局部依赖信息。
这一方法结合了房价时序预测在长期整体趋势和短期局部的信息,降低了房价预测的方差,提高了多维时序数据房价预测方法的泛化能力。
其三是应用地理信息系统 (GIS),将深度学习与地理信息系统 (GIS) 相结合,分析地理位置等因素对房价的影响,提高模型的预测准确性——前文所述的 osp-GNNWR 模型就是典型代表之一。
有了 AI 的加持,房价预测模型将变得更可靠和精确。基于此,房产企业能够降低投资风险;政府则可以全面精准的掌控住房信息,从而有的放矢地进行管理,共同打造良好的房地产环境,帮助老百姓真正做到安居乐业。
参考资料:
1.https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2343771
2.https://mp.weixin.qq.com/s/P4nk5sl2v60Q5DeVrOfWLw
3.https://cloud.baidu.com/article/1892933
4.https://patents.google.com/pate