By 超神经
标题有些危言耸听,前几天我们也写过图灵的八卦了,他被业界奉为「人工智能之父」毋庸置疑。
今天写的这位长者,也是位不得了的人物——香农,学界尊称他为「信息科学之父」。大家都知道,信息论对人工智能实业的推动之大,所以我们就称香农为「人工智能之舅老爷」。

青年香农时的俊朗自信,还是发明家爱迪生的远方亲戚
1916 年 4 月 30 日,克劳德·香农出生于美国密歇根州一个叫做 Gaylord 的小镇,此时的图灵远在英国,已经成长到四岁。香农在 1936 年获得密歇根大学的数学与电气工程学士学位 。 1940 年在 MIT 获得数学硕士和博士学位,1941 年进入贝尔实验室工作。
相比于图灵,香农的人生更加顺遂一些,他于 2001 年 2 月 26 日去世,享年 84 岁。
舅老爷对 AI 事业的鼎力相助
香农所开创的信息论,不单单是信息通信科学的基石,直至今日,仍然是是深度学习的重要理论依据。
信息论综合运用了微积分、概率论和统计学等诸多学科,在深度学习中,也起到了非常重要的作用:
-
常见的交叉熵损失函数;
-
在最大信息增益的基础上构建决策树;
-
在 NLP 和演讲中广泛使用的 Viterbi 算法;
-
在机器翻译中常用的 RNN 和各种类型的模型中普遍使用的编码器和解码器;
信息论の发展简史
我们从一个简单的例子来引入,在下面两个句子里,包含了不同的信息量。
「Bruno 是条狗。」
「Bruno 是一条棕色的大狗。」
很明显,这两个句子传达出的信息量不同,跟第一句话相比,第二句话信息量更丰富,不仅告诉我们 Bruno 是条狗,还告诉我们狗的毛色和体型。
但就这两个简单句子,在 20 世纪早期,让科学家和工程师们最头疼的问题。
他们希望量化这些信息之间的差异,并从数学角度来对这些信息进行描述。
遗憾的是,当时并没有一种现成的分析方法,或数学方法可以做到这一点。
之后,科学家们一直在苦寻这个问题的答案,希望从数据的语义等方面找到答案。但结果证明,这样的研究除了增加问题的复杂性,再无它用。
直到香农,作为一个数学家兼工程师,在该问题上引入 「熵」的概念后。信息的量化度量问题终于得到解决,这也标志着我们开始进入「数字信息时代」。
香农并没有把精力花在对数据的语义研究上,而是通过概率分布和 「不确定性」来量化信息,并引入 「bit」概念来度量信息量。
他认为,当涉及到信息内容时,数据的语义并不重要。
这一革命性的思想不仅为信息理论奠定了基础,也为人工智能等领域的发展开辟了新的道路。因此,克劳德·香农,也被公认为信息时代之父。
深度学习中的常见元素:熵
信息论应用场景众多,这里我们主要看看它在深度学习和数据科学领域四种比较常见的应用。
熵(Entropy)
又叫信息熵或香农熵,用于度量具有不确定的结果,我们可以通过下面两个实验来理解:
-
抛一枚均匀的硬币, 使得结果出现概率为 0.5;
-
抛一枚存在偏差的硬币,使结果出现概率为 0.99;
很明显,跟实验 1 相比,我们更容易预测实验 2 的结果。因此,从结果来看,实验 1 比实验 2 更具不确定性,而熵就是专门用来度量这个不确定性。
如果实验结果的不确定性越多,那么它的熵就越高,反之就越低。
一个完全可以肯定结果的确定性实验中,熵为零。在一个完全随机的实验中,比如公平的骰子,每种结果都存在很大的不确定性,其熵就会很大。
另一种确定熵的方法是,把观察随机实验结果时获得的平均信息,做为定义熵的函数。结果越少,观察到的信息也就越少,熵就越小。
例如,在确定性实验中,我们总是知道结果,所以从观察结果中没有得到新的信息,因此熵为零。
数学公式
对于一个离散的随机变量 X,可能产生的结果记做 x_1,…,x_n , 则熵的计算公式如下(熵用 H 表示,单位 bit):
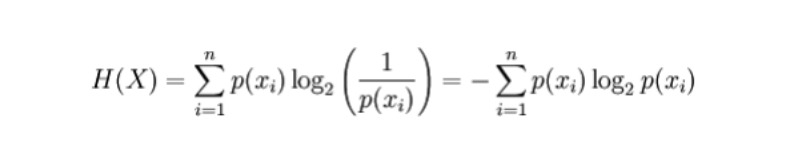
其中,p(x_i) 是变量 X 所产生的结果的概率。
应用
-
构建自动决策树,在构建过程中,所有功能的选择都可以使用熵的标准来完成。
-
熵越大,信息量也就越多,也就更具预测价值。可以据此从相互竞争的两个模型中找出最有价值的模型,即熵最高的模型。
深度学习中常见的重要元素:交叉熵
交叉熵(Cross-Entropy)
定义:交叉熵主要用于度量两个概率分布间的差异性信息,它可以告诉我们这两个概率有多相似。
数学公式
在同一个样本中定义的两个概率 p 和 q 的交叉熵计算公式为(熵用 H 表示,单位 bit):
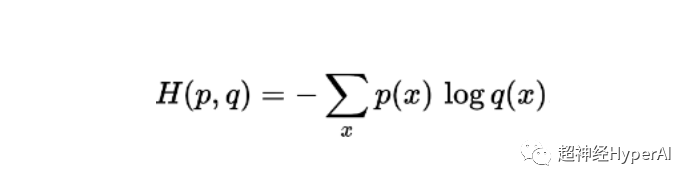
应用
-
交叉熵损失函数广泛应用于 Logistic 回归等分类模型。当预测偏离真实输出时,交叉熵损失函数增加。
-
在像 CNN 这样的深度学习体系结构中,最终输出的 “softmax” 层经常使用交叉熵损失函数。
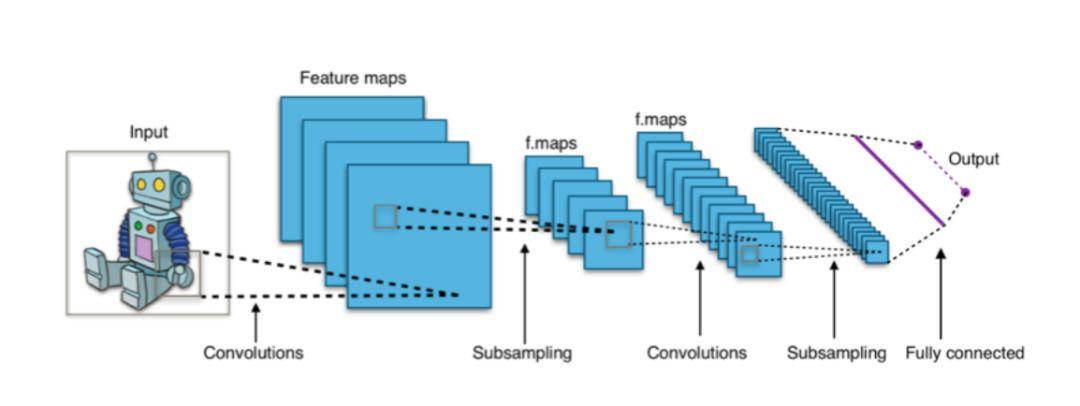
图注:基于 CNN 的分类器通常把 softmax 层作为最终层,使用交叉熵损失函数进行训练
深度学习中常见的重要元素:互信息
互信息(Mutual Information)
定义互信息用来度量两个概率分布或随机变量之间相互依赖程度,简单来讲就是一个变量有多少信息被另一个变量携带。
互信息捕获的随机变量之间的相关性,不同于一般性相关仅局限在线性领域,它还可以捕获一些非线性相关信息,其应用范围也更广。
数学公式
两个离散随机变量 X 和 Y 的互信息公式为:
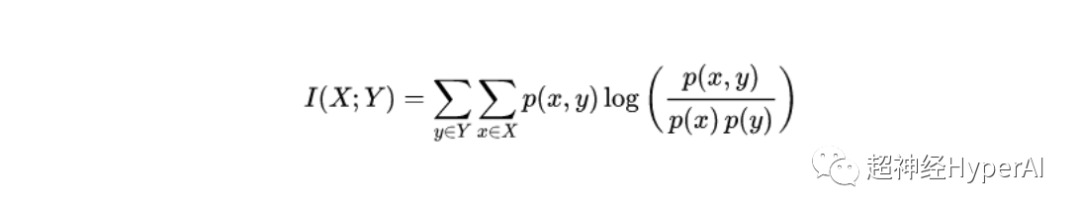
其中 p(x,y) 为 x 和 y 的联合概率分布,p(x) 和 p(y) 分别为 x 和 y 的边际概率分布。
应用
- 特征选择:互信息不仅可以捕捉线性相关,还能关注到非线性相关,在进行特征选择时更全面,准确度也更高。
- 在贝叶斯网络中,互信息被用来学习随机变量之间的关系结构,并定义这些关系的强度。
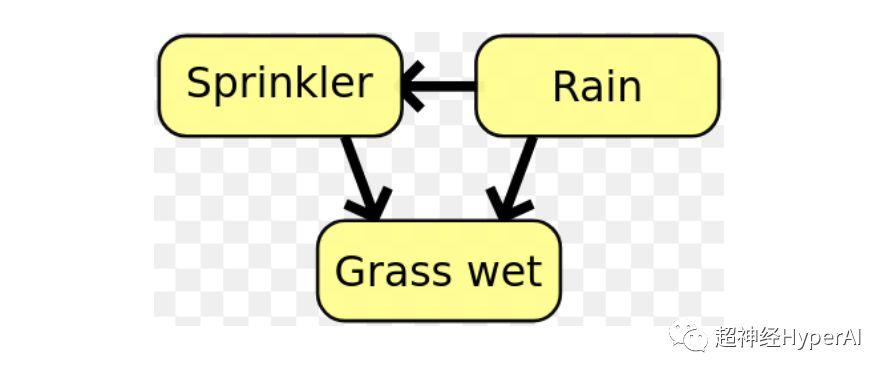
图注:在贝叶斯网络中,变量之间的关系结构可以使用互信息来确定
深度学习中常见的重要元素:KL 散度
KL 散度(Kullback–Leibler divergence)
KL 散度又叫相对熵,用来衡量两个概率分布的偏离程度。
假设我们需要的数据在真实分布 P 里,但我们不知道这个 P,这时我们可以新建概率分布 Q,来拟合真实分布 P 。
由于 Q 里面的数据只近似于 P,因此 Q 没有 P 精确。所以,Q 相对于 P 而言,会出现部分信息丢失的情况,这部分丢失的信息量就由 KL 散度度量。
KL 散度可以告诉我们,当我们决定使用 Q(P 的近似数据)时,我们将损失多少信息。 KL 散度越趋近于零,Q 里面的数据也就越接近于 P 。
数学公式
一个概率分布 Q 与另一个概率分布 P 的 KL 散度的数学公式为:
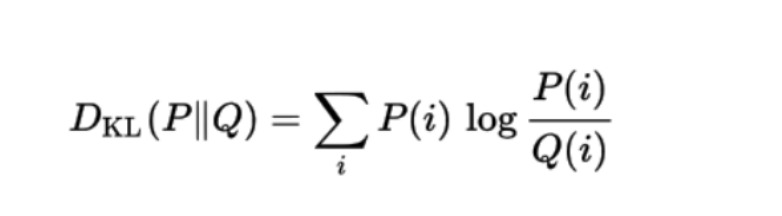
应用
KL 散度目前多用于无监督机器学习系统中的 VAE(变分自动编码器)。
1948 年,克劳德·香农在独具开创性的论文《通信的数学理论》中正式提出「信息论」,开启一个新时代。如今,信息论已经被广泛使用于机器学习、深度学习和数据科学等诸多领域。
第一届香农奖
大家都知道,计算机界最高荣誉奖项是图灵奖。图灵奖是 1966 年起,由美国计算机学会为了纪念图灵的卓越贡献而设立。同样,在信息领域中香农奖的地位同样重要。
不一样的是,图灵早在 1954 年就去世了,并没有机会知道世人为他设置了这个奖项。
而香农则幸运得多,香农奖由 IEEE 学会在 1972 年设立,为了表彰在信息论领域有着卓越贡献的科学家和工程师,在第一届里,香农自己领取了香农奖。

「香农获得香农奖,史称香农套路」