시그모이드 함수
시그모이드 함수이는 일반적인 S자 모양 함수로, S자 모양 성장 곡선이라고도 합니다. 시그모이드 함수는 단조 증가 및 역단조 증가 특성을 가지므로, 변수를 0과 1 사이로 매핑하는 신경망의 임계값 함수로 자주 사용됩니다.
시그모이드 함수의 기본 속성
시그모이드 함수의 형태와 이미지는 다음과 같습니다.
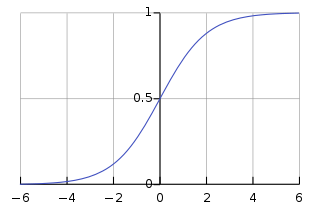
- 도메인: ( −∞ , +∞ )
- 범위: (− 1 , 1 );
- 함수는 정의 영역 내에서 연속적이고 매끄러운 함수입니다.
- 이는 어디에서나 미분 가능하며, 그 미분은 다음과 같습니다. f′(x) = f(x)(1−f(x));
- 이 함수는 0과 1 사이의 값을 취하고, 0.5에서 중심 대칭을 이루고, x = 0에 가까워질수록 기울기가 커집니다.
시그모이드 함수와 로지스틱 회귀
로지스틱 회귀 LR의 목적에 따라 함수를 선택할 때 다음 두 가지 조건이 충족되어야 합니다.
1) 값의 범위는 0과 1 사이입니다.
2) 이벤트 발생의 경우 50%가 결과의 분수령이며, 선택 함수는 0.5를 중심으로 대칭적이어야 합니다.
이 두 가지 점을 기반으로 볼 때, 시그모이드는 LR의 요구 사항을 충족합니다.