Fonction sigmoïdeIl s’agit d’une fonction en forme de S courante, également connue sous le nom de courbe de croissance en forme de S. En raison de ses propriétés monotones croissantes et inversement croissantes, la fonction sigmoïde est souvent utilisée comme fonction de seuil d'un réseau neuronal pour mapper des variables entre 0 et 1.

Propriétés de base de la fonction sigmoïde

La forme et l'image de la fonction sigmoïde sont les suivantes :

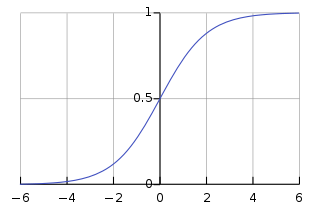
• Domaine : ( −∞ , +∞ )
• Plage : (− 1 , 1 );
• La fonction est une fonction lisse continue dans le domaine de définition ;
• Elle est différentiable partout, et sa dérivée est : f′ ( x ) = f ( x ) ( 1 − f ( x ) );
• La fonction prend des valeurs comprises entre 0 et 1, est symétrique au centre à 0,5 et présente une pente plus grande à mesure qu'elle s'approche de x = 0.

Fonction sigmoïde et régression logistique

Conformément à l'objectif de la régression logistique LR, les deux conditions suivantes doivent être remplies lors de la sélection de la fonction :

1) La plage de valeurs est comprise entre 0 et 1 ;

2) Pour une occurrence d'événement, 50% est le seuil du résultat et la fonction de sélection doit être symétrique autour de 0,5.

Sur la base de ces deux points, Sigmoid répond parfaitement aux besoins de LR.

Termes connexes : régression logistique, fonction de valve