Analyse De La Réponse Dynamique Non Linéaire Du Tremblement De Terre De Koyna En Tenant Compte De La Pression Hydrodynamique
Introduction au tutoriel
Introduction à Abaqus
Abaqus est un puissant logiciel d'analyse par éléments finis (FEA) largement utilisé dans le domaine de la simulation d'ingénierie. Il simule et analyse divers problèmes d'ingénierie grâce à la méthode des éléments finis et peut gérer des problèmes allant des problèmes linéaires simples aux problèmes non linéaires complexes. Abaqus a été initialement publié en 1978 et développé par Hibbitt, Karlsson & Sorensen, Inc. (HKS), qui a ensuite été renommé ABAQUS et acquis par Dassault Systèmes en 2005.
Introduction au tutoriel
Ce tutoriel est le tutoriel officiel d'Abaqus :Analyse sismique d'un barrage-poids en béton. Cet exemple illustre une application typique du modèle de matériau de plasticité endommagé pour le béton afin d'évaluer la stabilité et les dommages des structures en béton soumises à des charges arbitraires.
Le tutoriel analyse le barrage de Koyna, qui a été frappé par un tremblement de terre de magnitude 6,5 sur l'échelle de Richter le 11 décembre 1967. Ce problème a été choisi car il a été largement analysé par de nombreux chercheurs, notamment Chopra et Chakrabarti (1973), Bhattacharjee et Léger (1993), Ghrib et Tinawi (1995), Cervera et al. (1996) et Lee et Fenves (1998).
Introduction aux paramètres de base
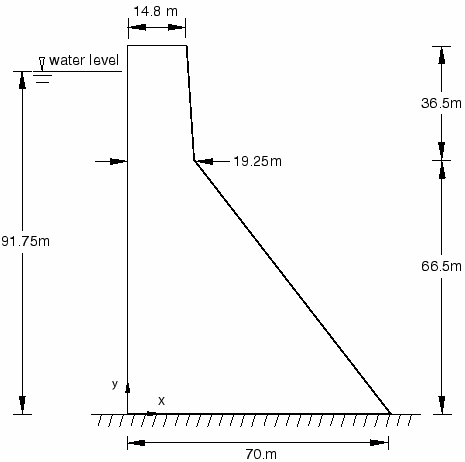
La géométrie transversale d'une section typique sans débordement du barrage de Koyna est illustrée à la figure 1. Cette section de barrage mesure 103 mètres de haut et 71 mètres de large à la base. La face amont de la section du barrage est supposée verticale. La profondeur de l'eau du réservoir au moment du tremblement de terre est de hw=91,75 m. Selon les chercheurs, une analyse bidimensionnelle de la section du barrage sans débordement dans des conditions de contrainte plane a été envisagée.
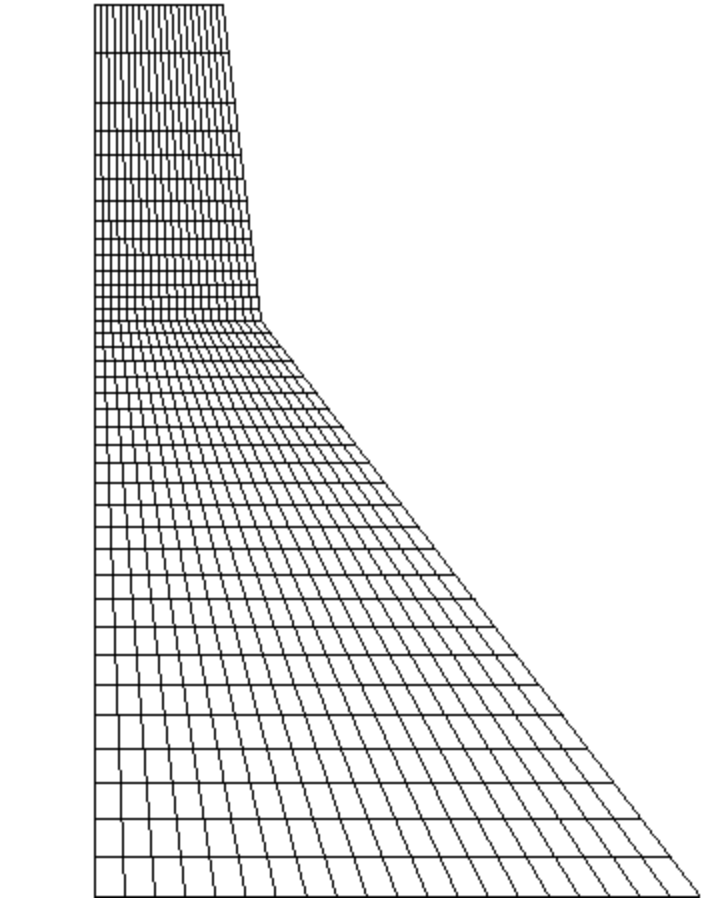
Le maillage d'éléments finis utilisé pour l'analyse est présenté dans la figure 2. Le maillage est composé de 760 éléments de contrainte plane à intégration réduite du premier ordre (CPS4R). Les nœuds sont définis dans un système de coordonnées rectangulaires global centré dans le coin inférieur gauche du barrage, avec l'axe vertical y pointant vers le haut et l'axe horizontal x pointant vers l'aval.
Dans cet exemple, nous ignorons l’interaction entre le barrage et la fondation en supposant que la fondation est rigide. L'interaction dynamique entre le barrage et le réservoir, due à la composante latérale du mouvement du sol, peut être modélisée sous une forme simple par la technique de masse ajoutée de Westergaard. Selon Westergaard (1933), la pression hydrodynamique exercée par l'eau sur le barrage lors d'un tremblement de terre équivaut à un certain volume d'eau se déplaçant d'avant en arrière avec le barrage, tandis que le reste du réservoir reste stationnaire. La masse additionnelle par unité de surface de la surface amont peut être exprimée par la formule approximative :
, où y ≤ hw, ρw=1000kg/m3 est la densité de l'eau. Dans l'analyse Abaqus/Standard, la méthode de masse ajoutée est mise en œuvre au moyen d'éléments utilisateur simples à 2 nœuds codés dans la sous-routine utilisateur UEL. Étant donné que la pression hydrodynamique générée par la composante verticale du mouvement du sol est considérée comme faible, elle est négligée dans toutes les simulations.
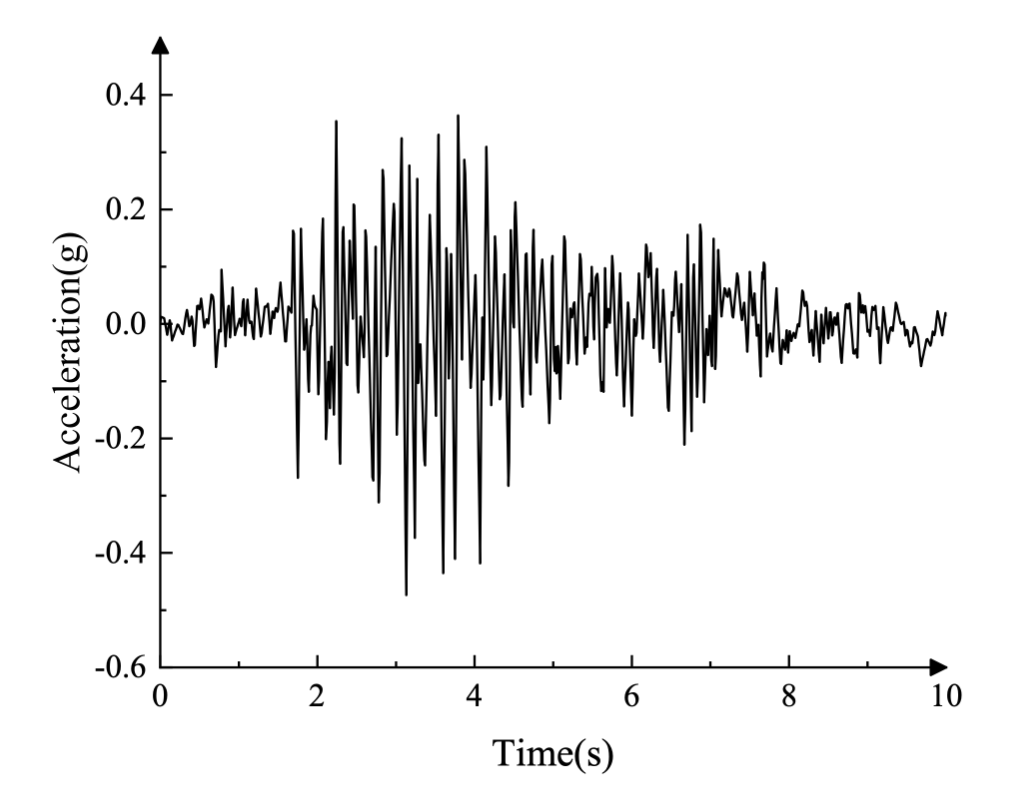
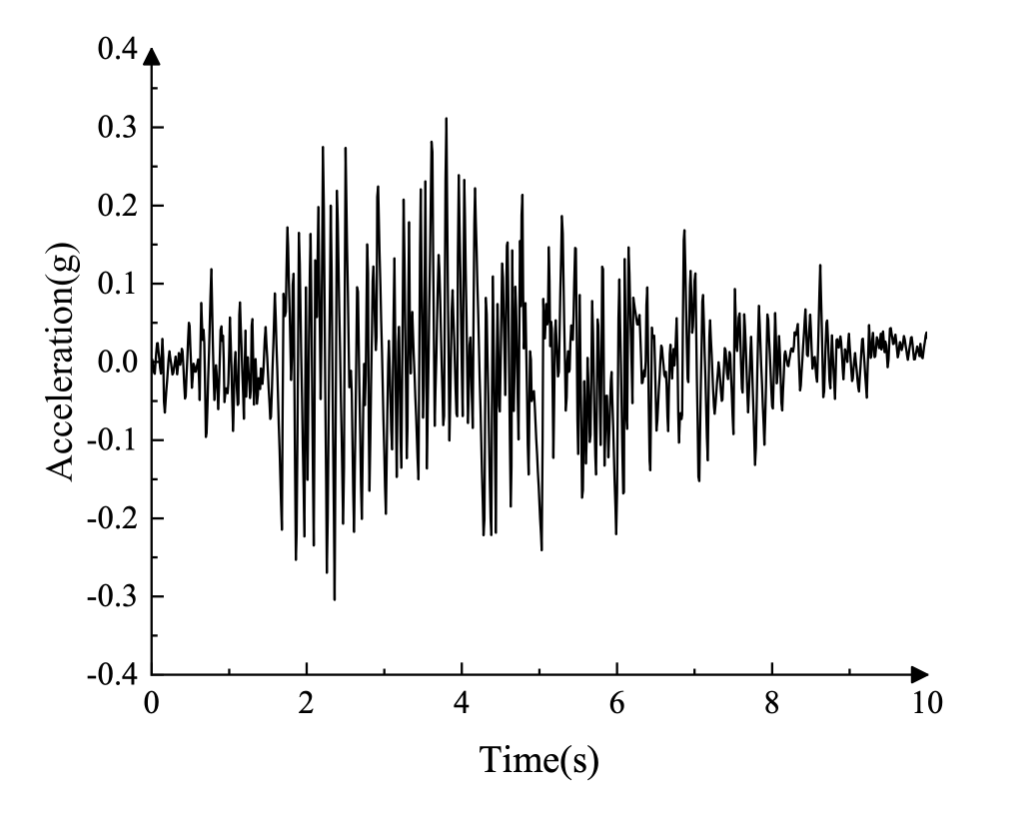
Les composantes latérales et verticales de l'accélération du sol enregistrées lors du séisme de Koyna sont présentées dans la figure 3 (en g = 9,81 m/s²). Avant l'excitation sismique, le barrage est soumis à des charges gravitaires générées par son propre poids et à la pression hydrostatique générée par le réservoir sur la face amont.
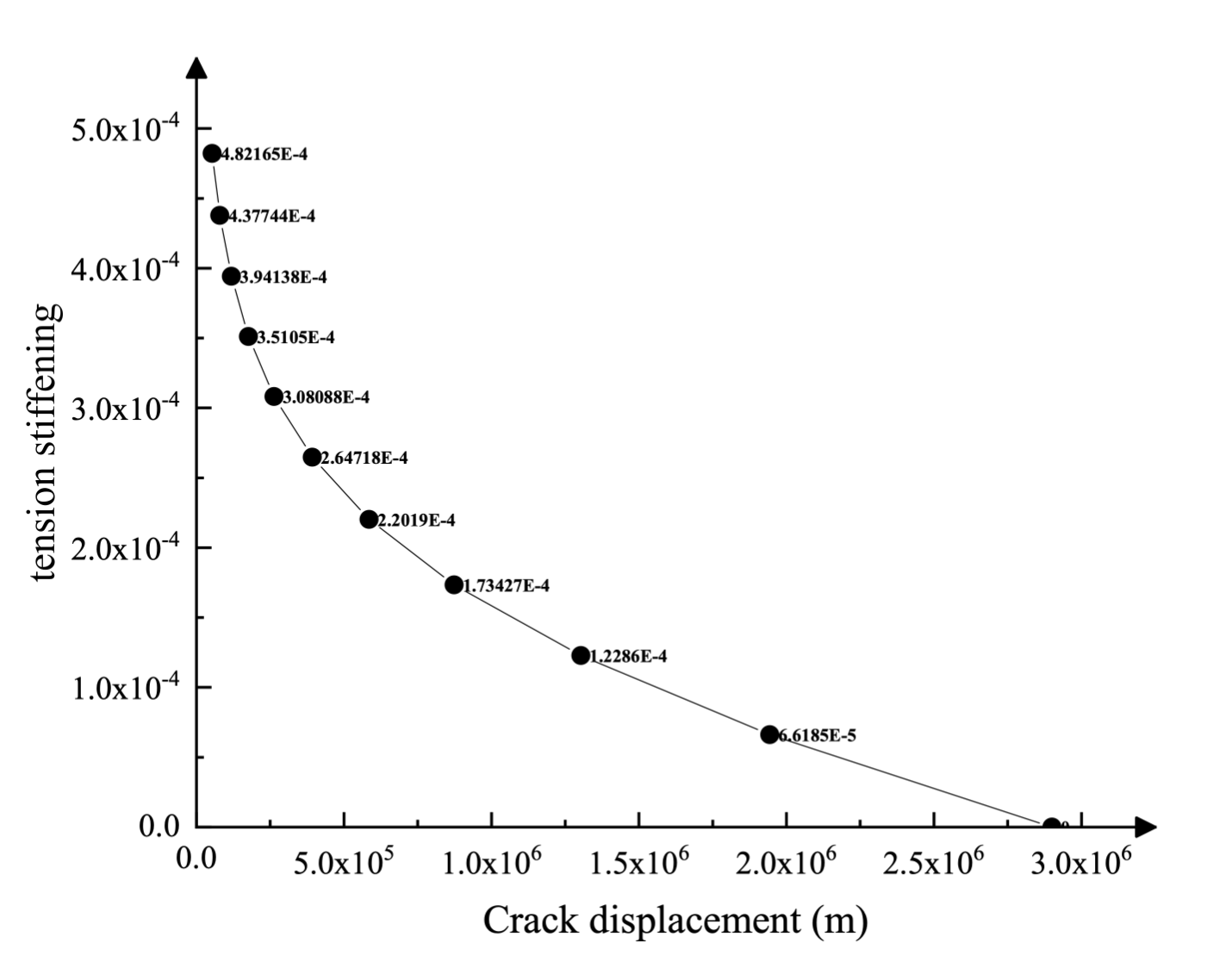
Le comportement mécanique du matériau béton est simulé par le modèle constitutif de plasticité des dommages du béton. Les propriétés des matériaux utilisés pour la simulation sont données dans le tableau 1 et la figure 4. Ces propriétés sont considérées comme représentatives du matériau en béton du barrage de Koyna et sont basées sur les propriétés utilisées par les chercheurs précédents. Pour obtenir ces propriétés matérielles, plusieurs hypothèses ont été formulées. L’étalonnage du comportement en traction du béton est particulièrement remarquable. La résistance à la traction est estimée comme la résistance ultime à la compression σcu = 10% de 24,1 MPa, et multiplié par un facteur d'amplification dynamique de 1,2 pour tenir compte des effets de taux ; par conséquent, σt0 = 2,9 MPa. Afin d'éviter des résultats inappropriés dus à la sensibilité du maillage en raison du manque de renforcement dans la structure, le comportement après rupture par traction est donné en spécifiant une courbe contrainte/déplacement plutôt qu'une courbe contrainte-déformation, comme illustré dans la figure 4.1. Ceci est réalisé grâce à la courbe contrainte/déplacement post-fissure.
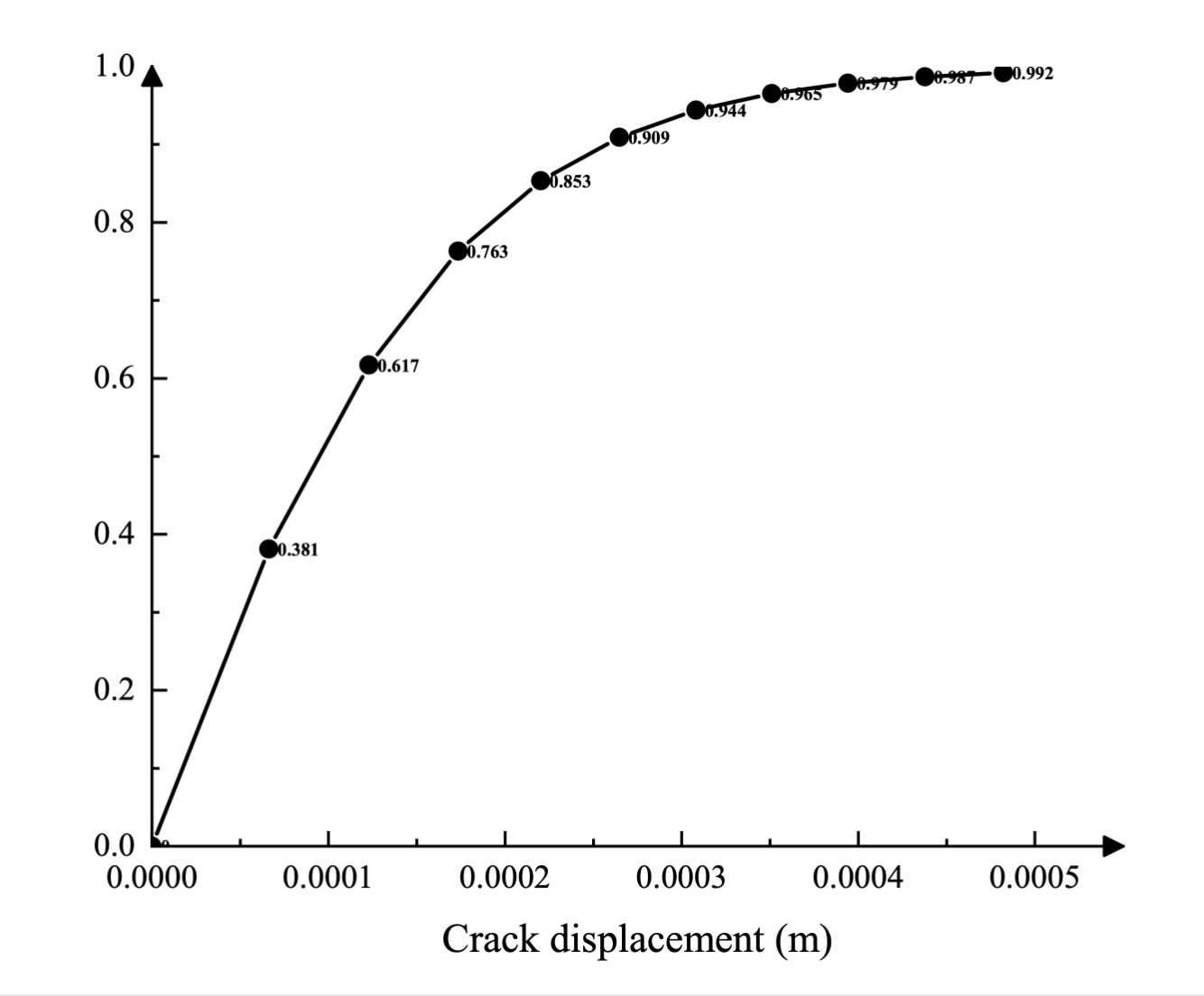
De même, les dommages dus à la traction sont spécifiés sous forme de tableau en fonction du déplacement de la fissure à l'aide d'une courbe de déplacement des dommages post-fissure. La courbe est illustrée dans la figure 4.2. Les dommages dus à la dégradation de la rigidité due à la rupture par compression (écrasement) du béton sont supposés être nuls.
Cas 1 : Analyse du domaine fréquentiel
L'analyse de fréquence des barrages en béton est d'une grande importance dans les projets de conservation de l'eau, principalement dans les aspects suivants :
1. Évaluation des performances sismiques
Les barrages en béton de grande hauteur sont généralement situés dans des zones sujettes aux tremblements de terre, et la résistance sismique est la clé de leur fonctionnement sûr. Grâce à l’analyse fréquentielle, nous pouvons comprendre les caractéristiques de réponse dynamique du barrage sous l’action d’un tremblement de terre et évaluer sa résistance aux tremblements de terre. Par exemple, l’analyse de fréquence peut aider à déterminer les fréquences naturelles et les modes de vibration d’un barrage sous l’action d’un tremblement de terre, évaluant ainsi ses performances sismiques3.
2. Analyse des caractéristiques dynamiques
L’analyse de fréquence peut révéler les caractéristiques dynamiques du barrage, notamment la fréquence naturelle, le mode de vibration et le rapport d’amortissement. Ces caractéristiques dynamiques sont cruciales pour comprendre la réponse dynamique et le comportement du barrage. Par exemple, l’analyse de fréquence peut être utilisée pour comprendre les changements de la fréquence naturelle du barrage sous différents niveaux d’eau et conditions de charge, évaluant ainsi sa stabilité dynamique.
- La figure suivante montre les 4 premiers modes de vibration de Koyna
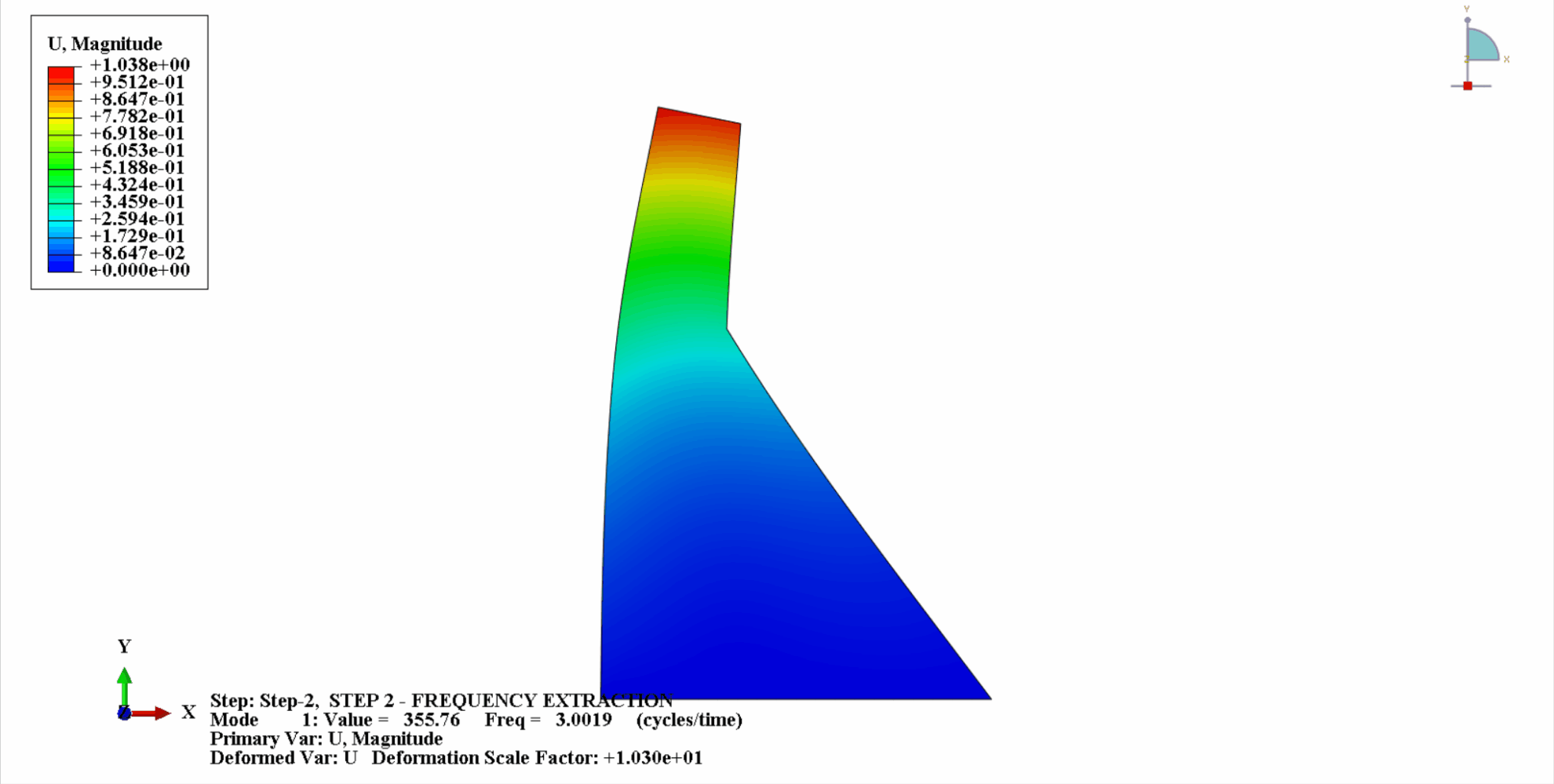
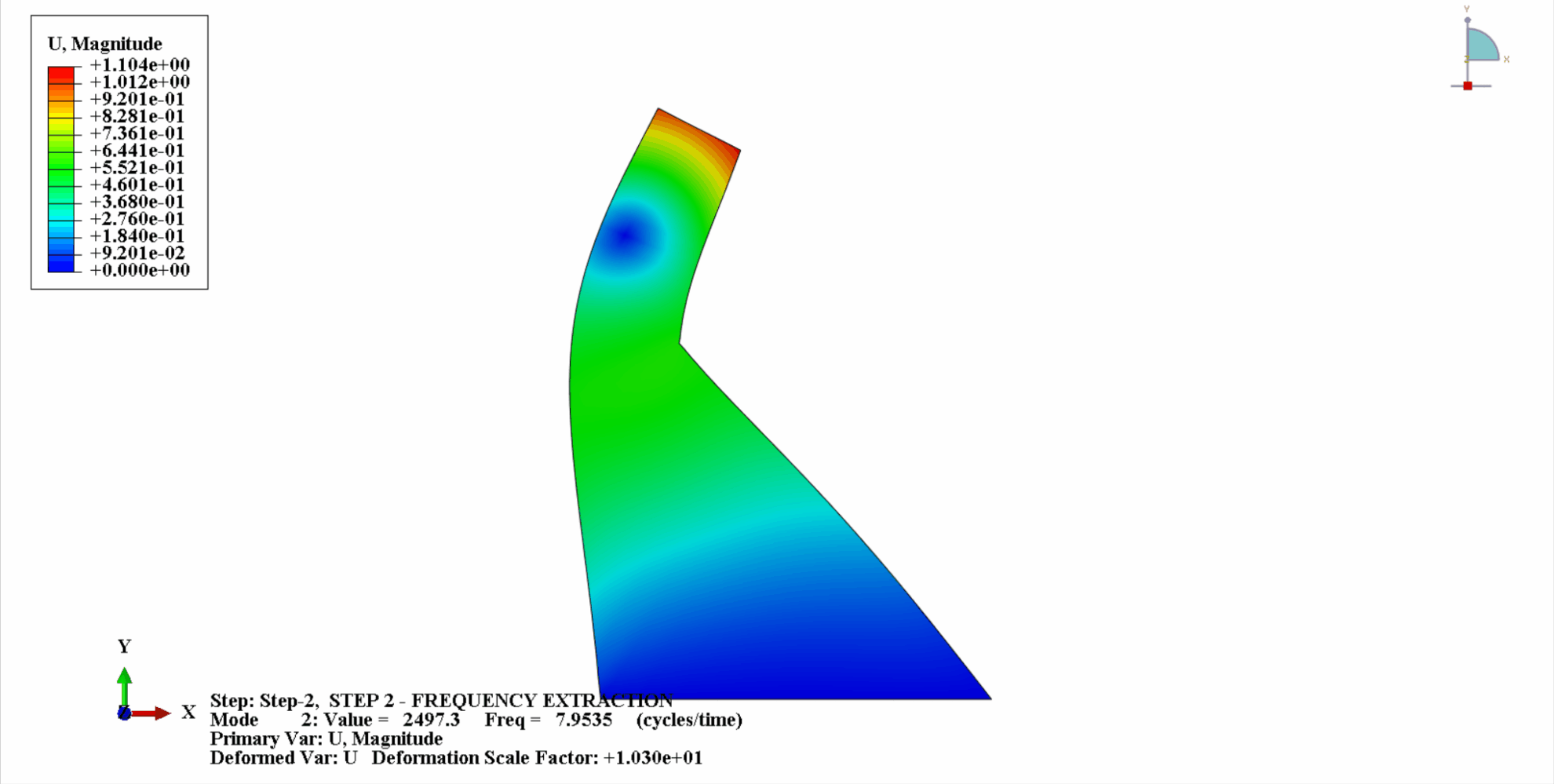
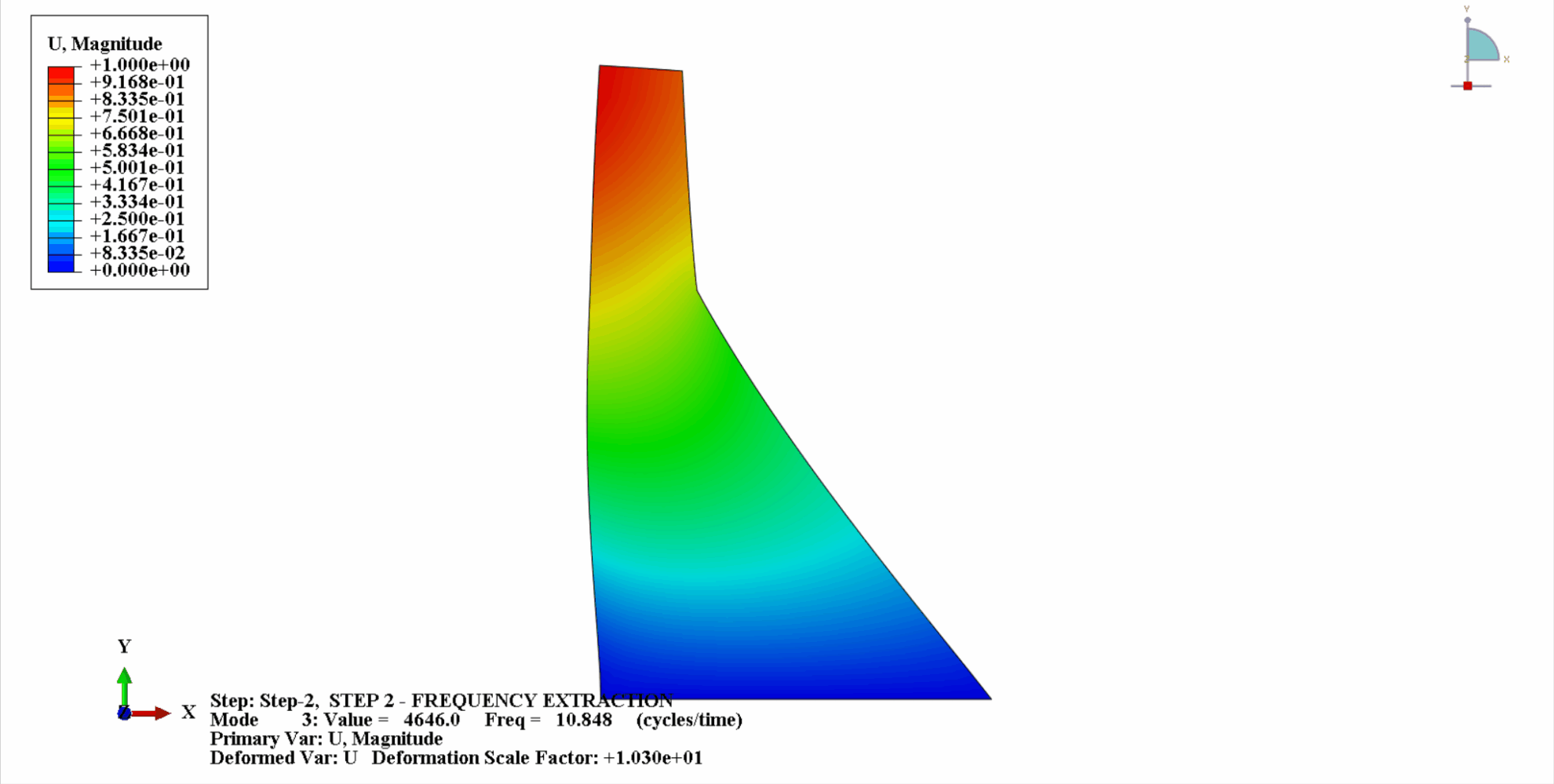
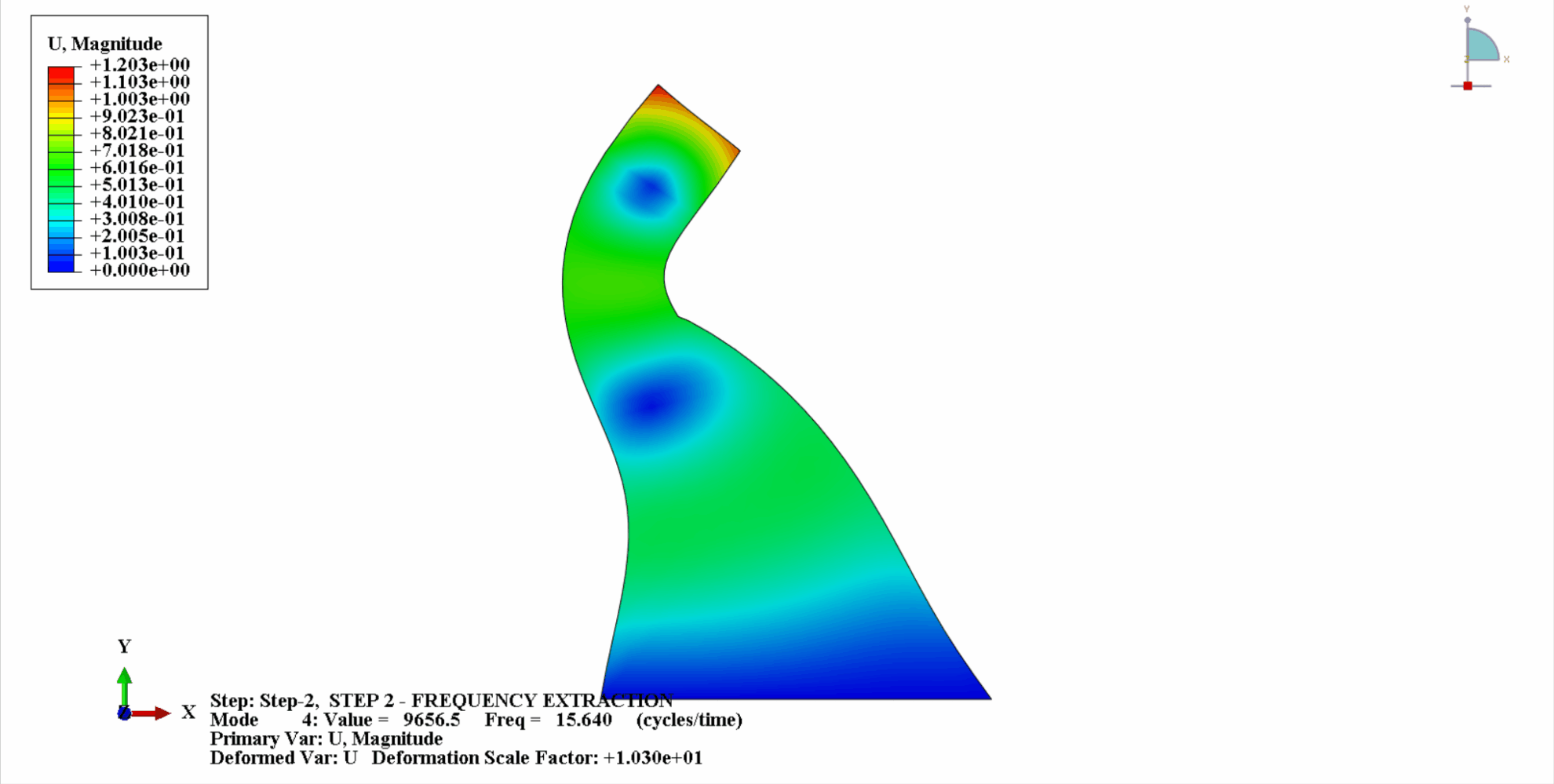
- Le tableau suivant montre la comparaison des fréquences naturelles : On peut voir que les résultats de calcul dans cet exemple sont cohérents avec les calculs de Chopra, et l'erreur de calcul est dans une plage acceptable.
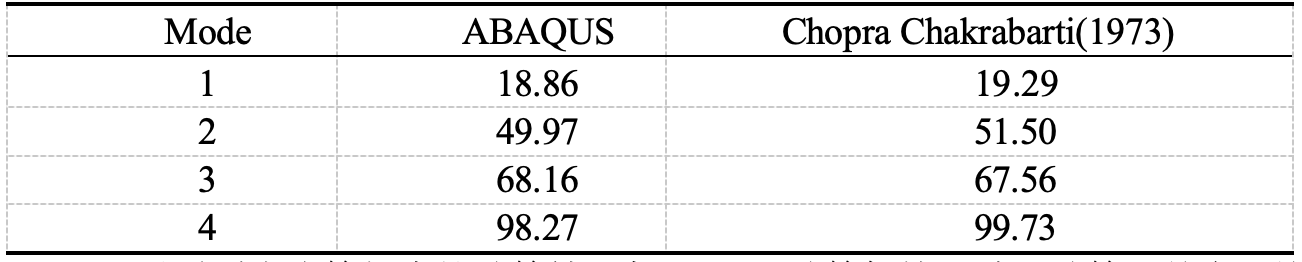
On peut voir que les résultats du calcul dans cet exemple sont cohérents avec le calcul de Chopra et que l’erreur de calcul se situe dans une plage acceptable.
Cas 3 : Analyse de la réponse sismique - prise en compte de la pression dynamique de l'eau
Dans l'analyse de la réponse sismique des barrages en béton, l'accent est mis principalement sur les données relatives entre la crête du barrage et la cloche du barrage, telles que les données de déplacement relatif, de vitesse relative et d'accélération relative.
* Ci-dessous se trouve la courbe chronologique du déplacement relatif de la crête et de la cloche du barrage le long de la rivière :
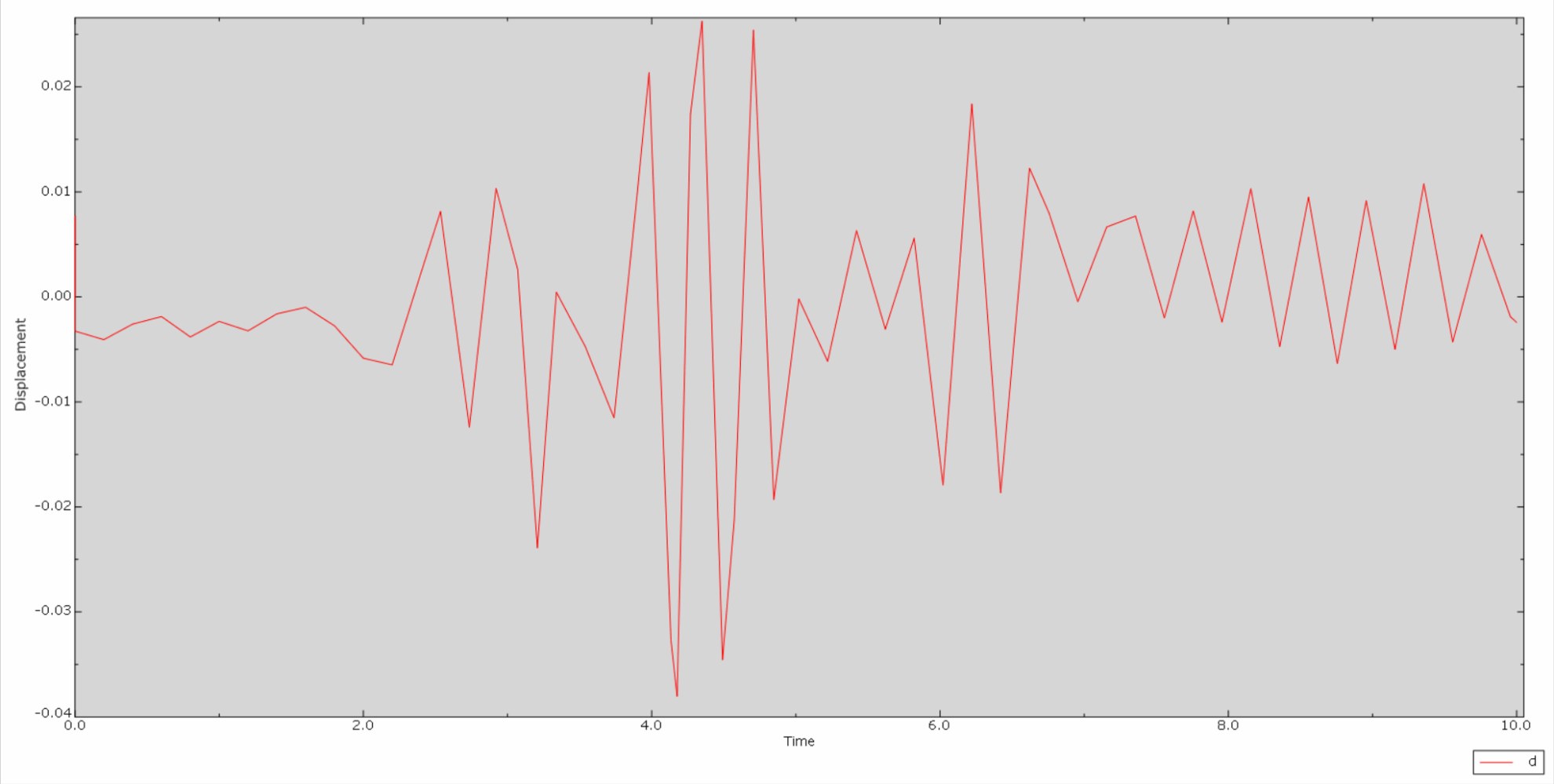
*Voici alors la courbe de l'historique de la vitesse relative de la crête et de la cloche du barrage :
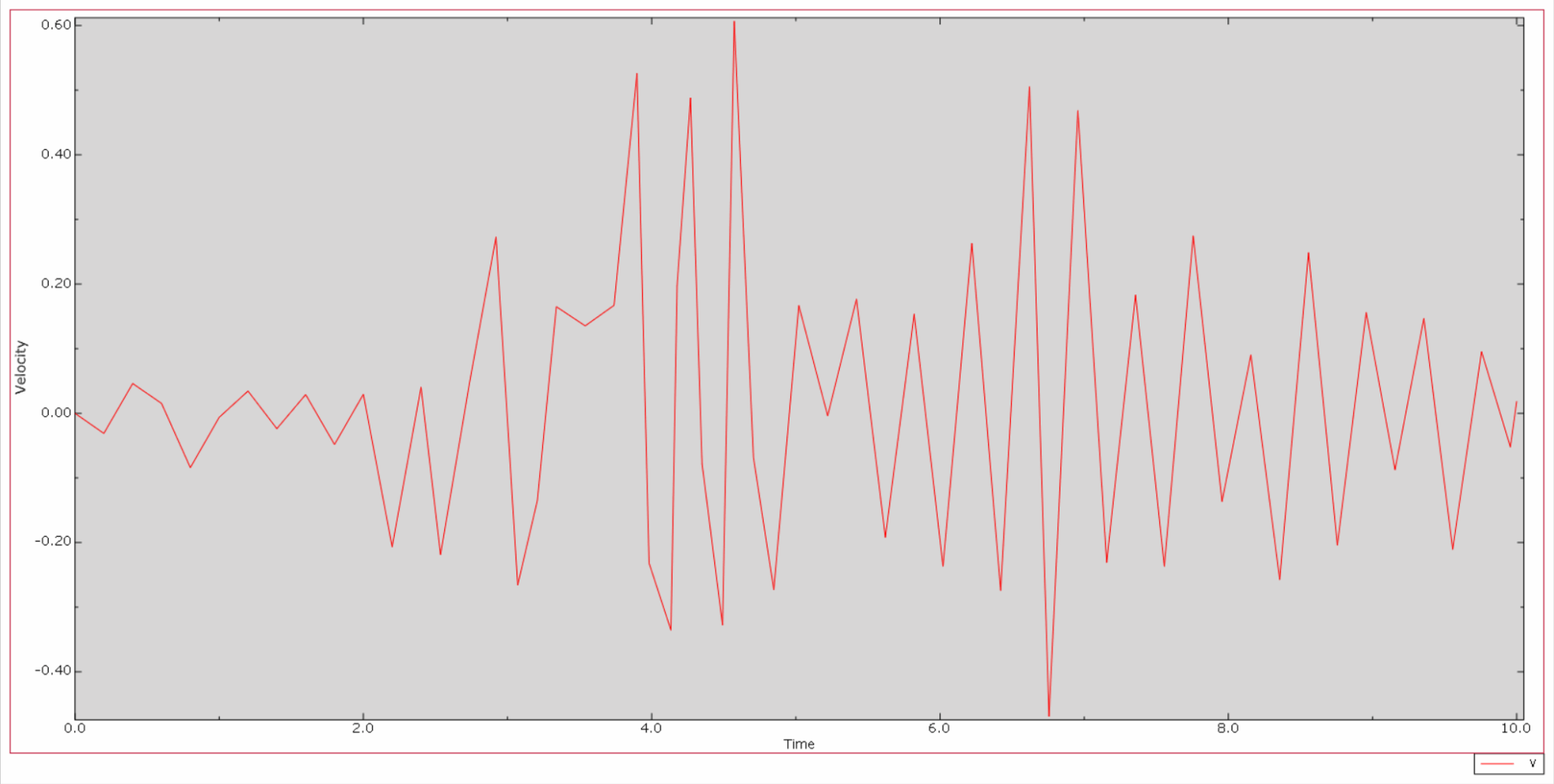
*Ensuite, la courbe d'accélération relative de la crête et de la cloche du barrage est la suivante :
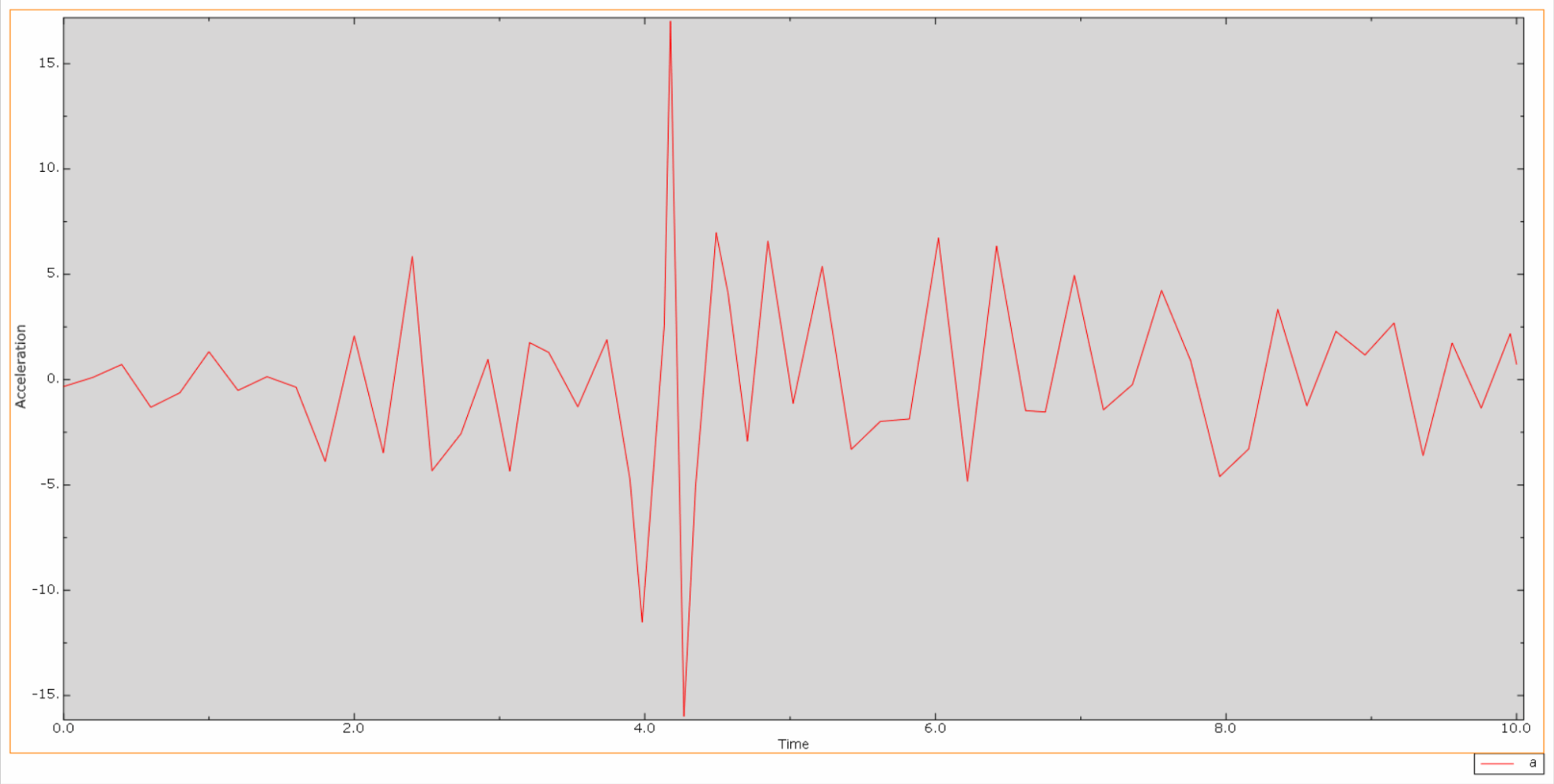
Sous l'action d'un tremblement de terre, le matériau du barrage en béton se trouve dans un état cyclique de tension-compression et le béton sera endommagé. Ce qui suit est un diagramme en nuage des dommages dus à la traction du corps du barrage à différents moments.
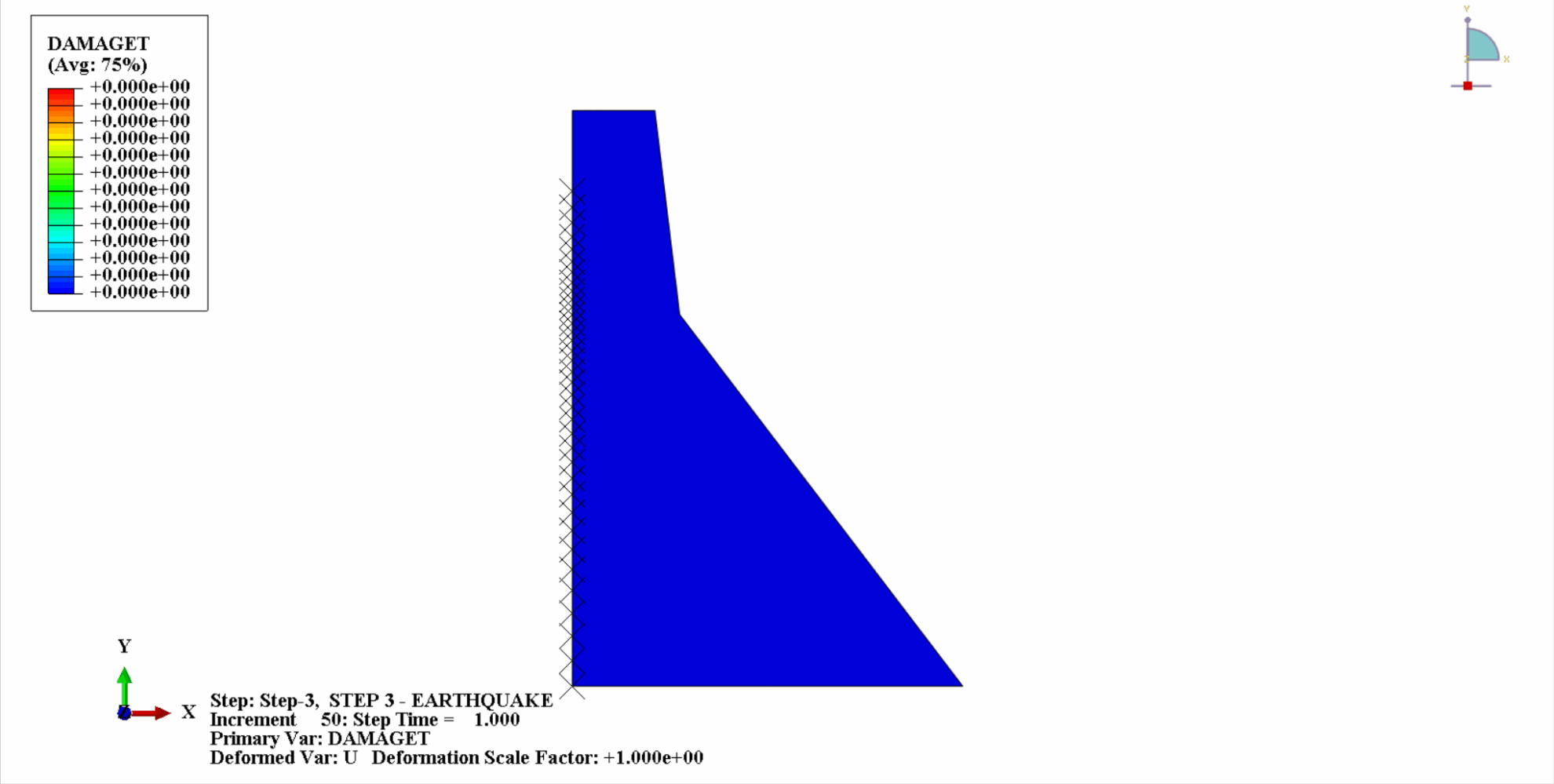
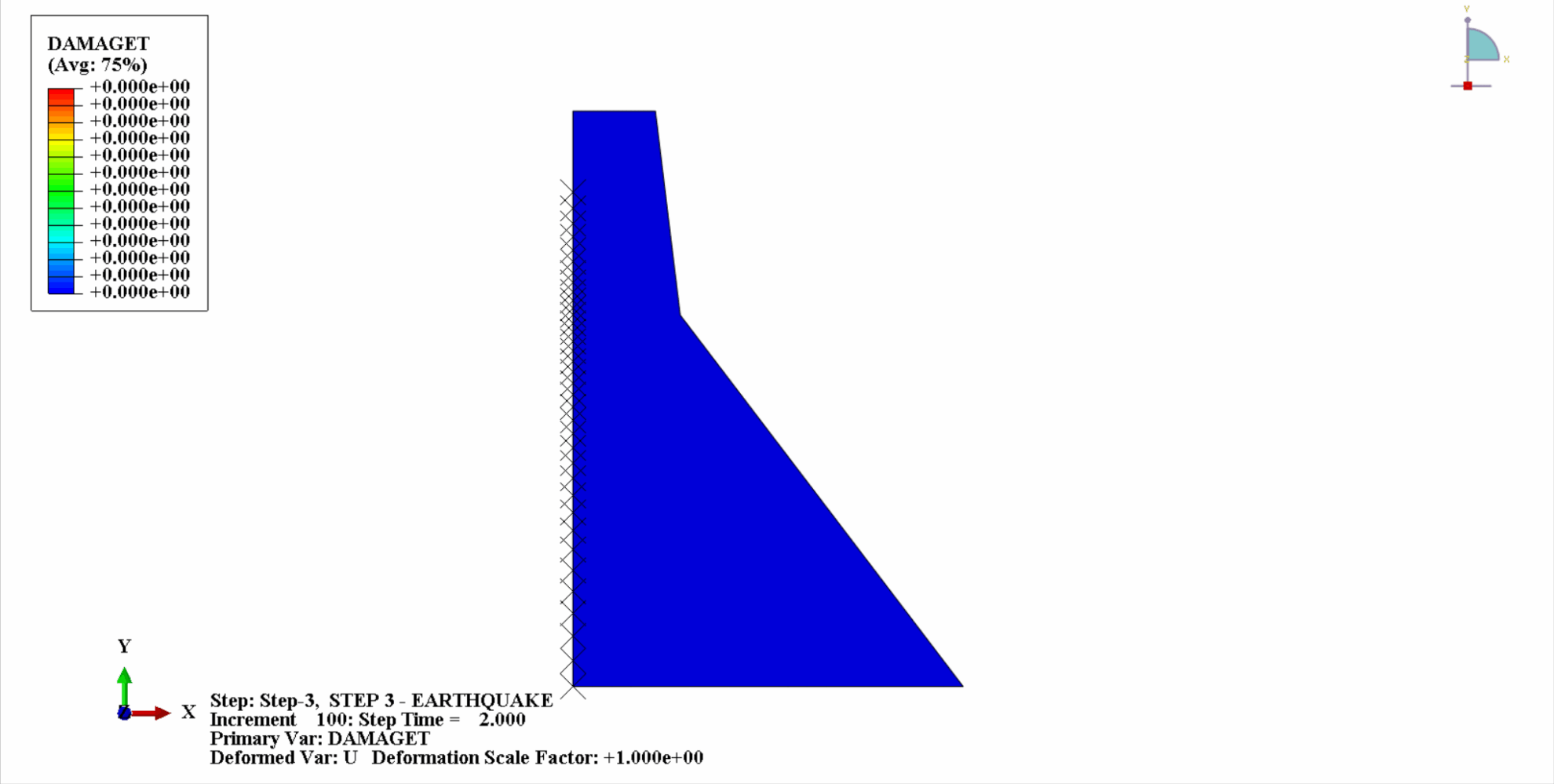
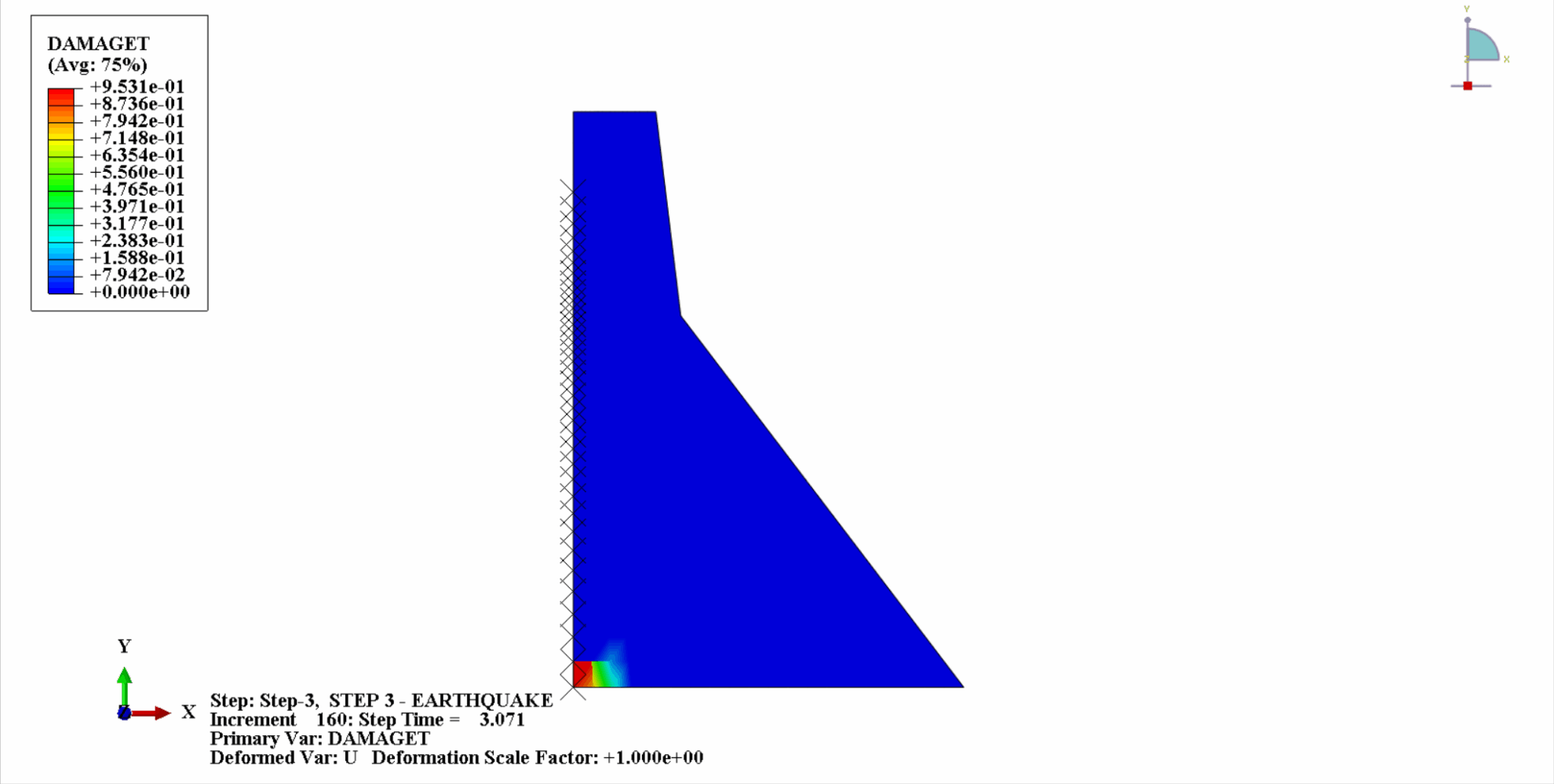
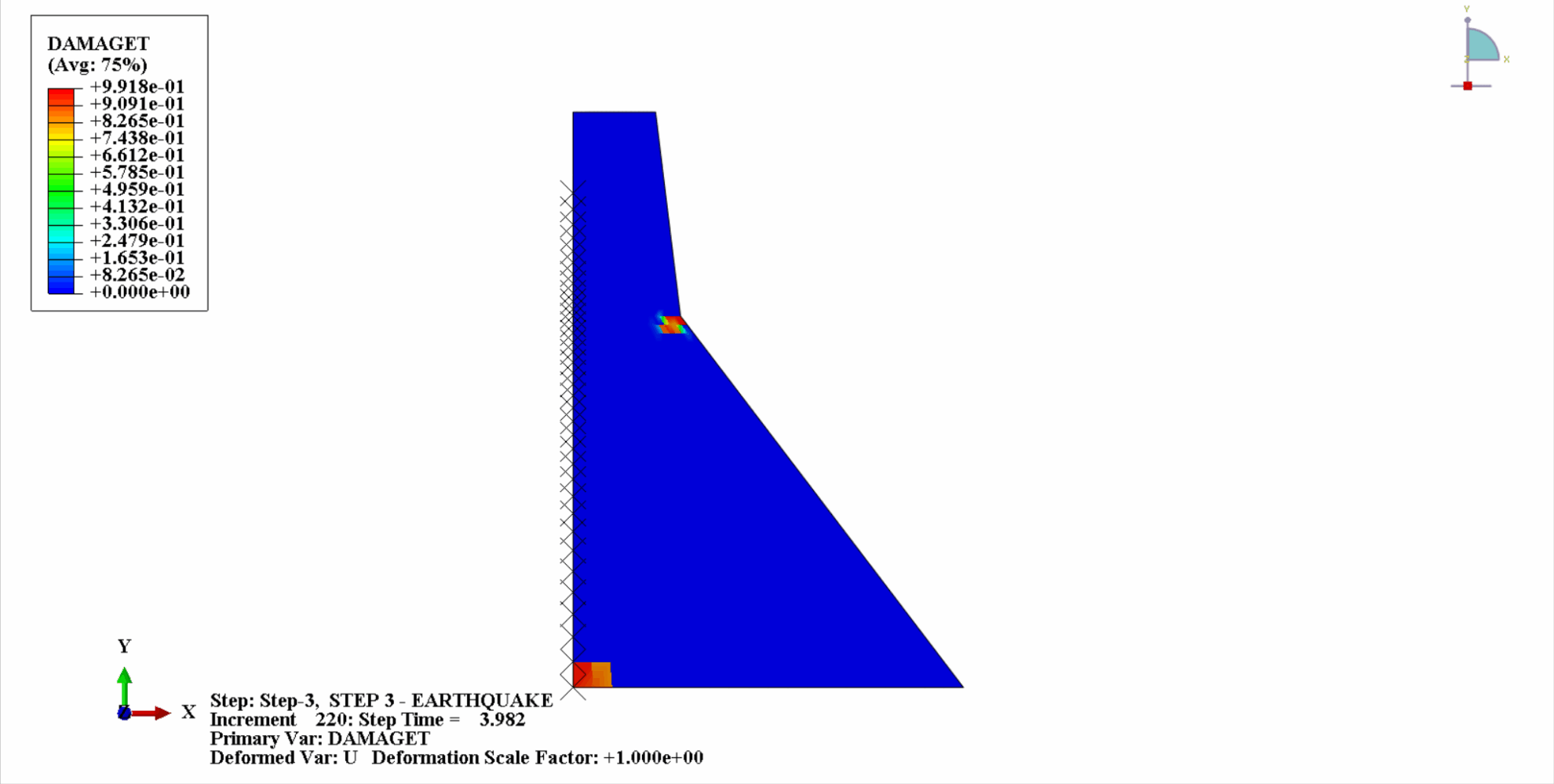
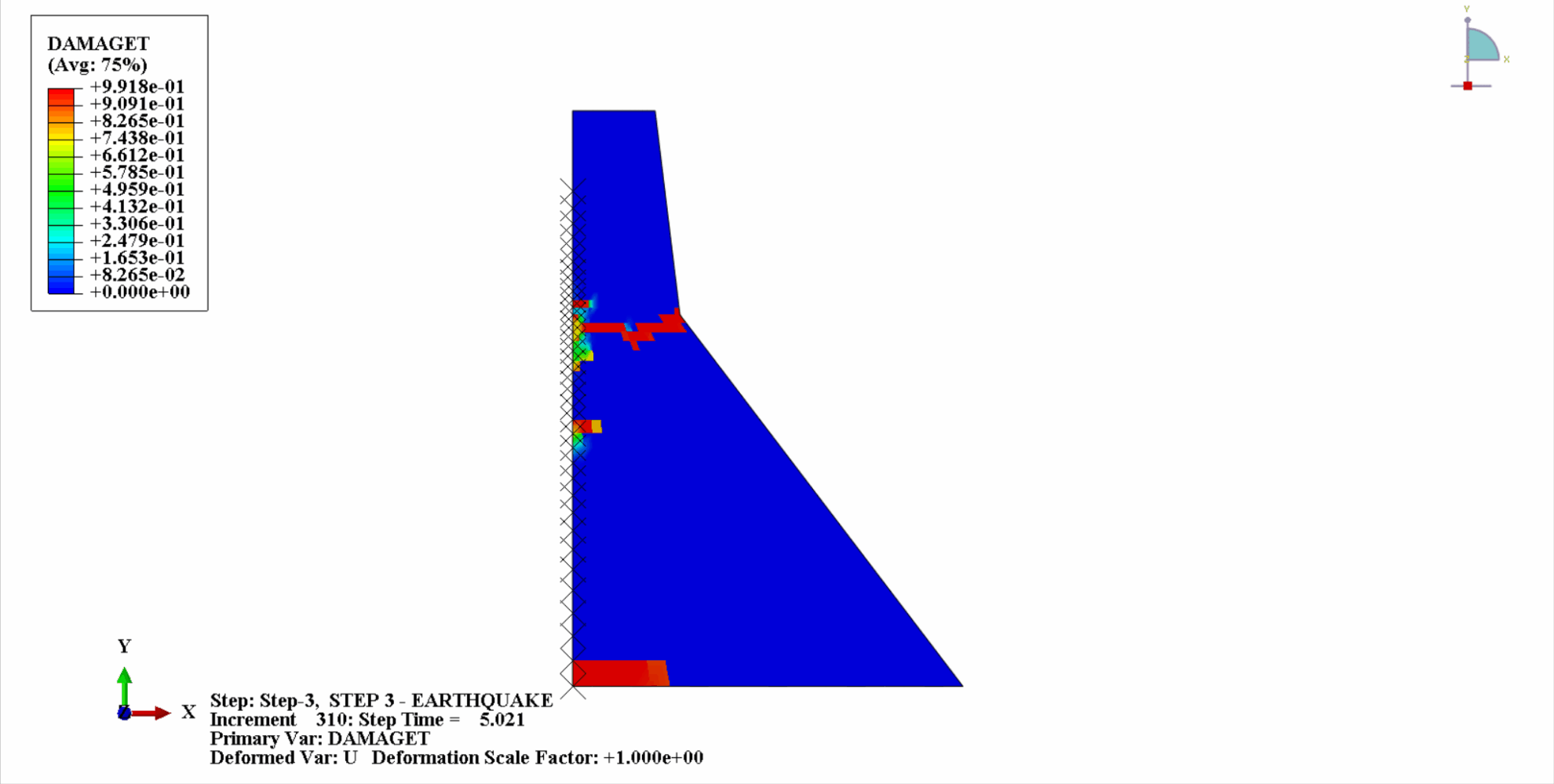
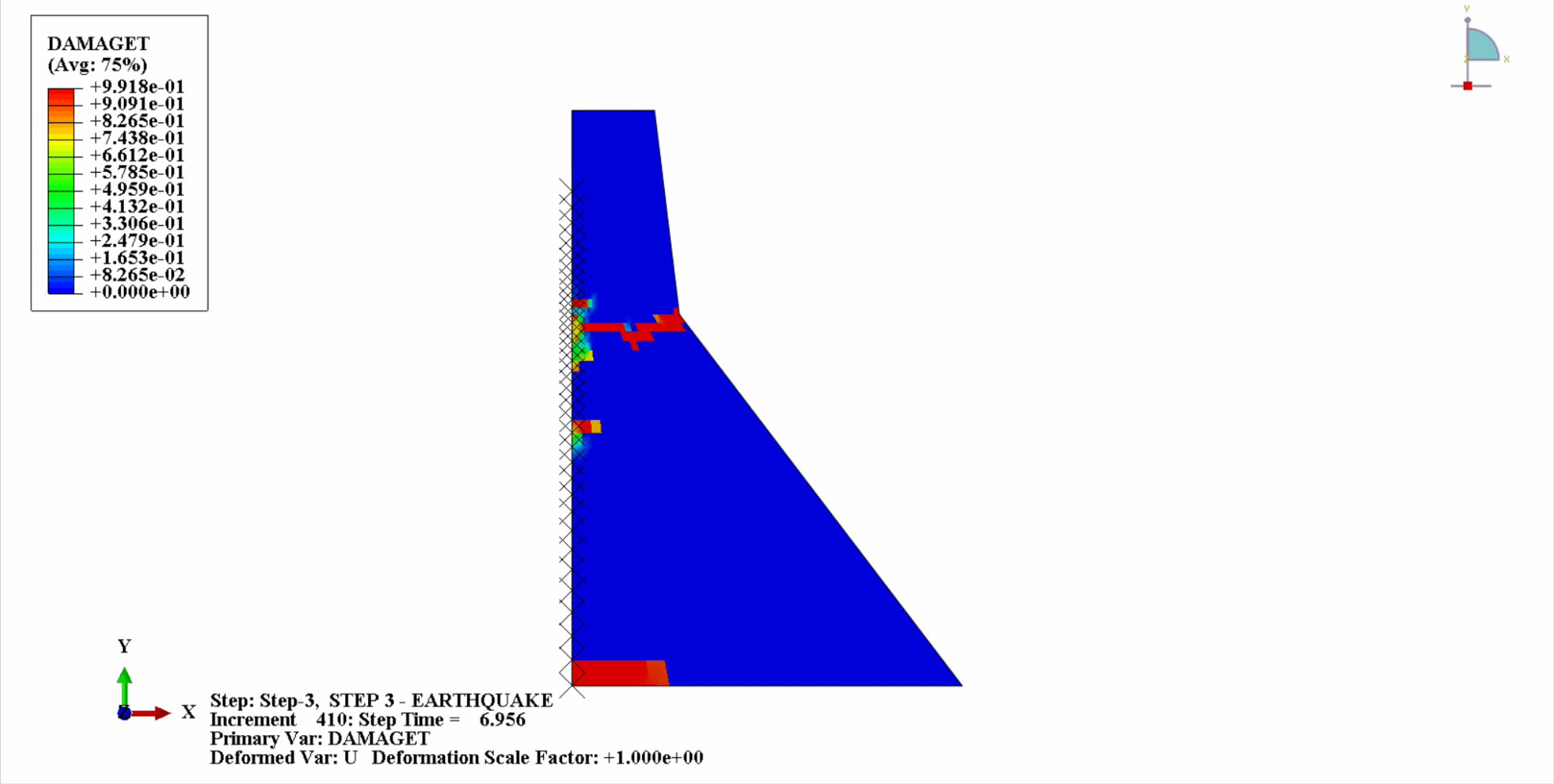
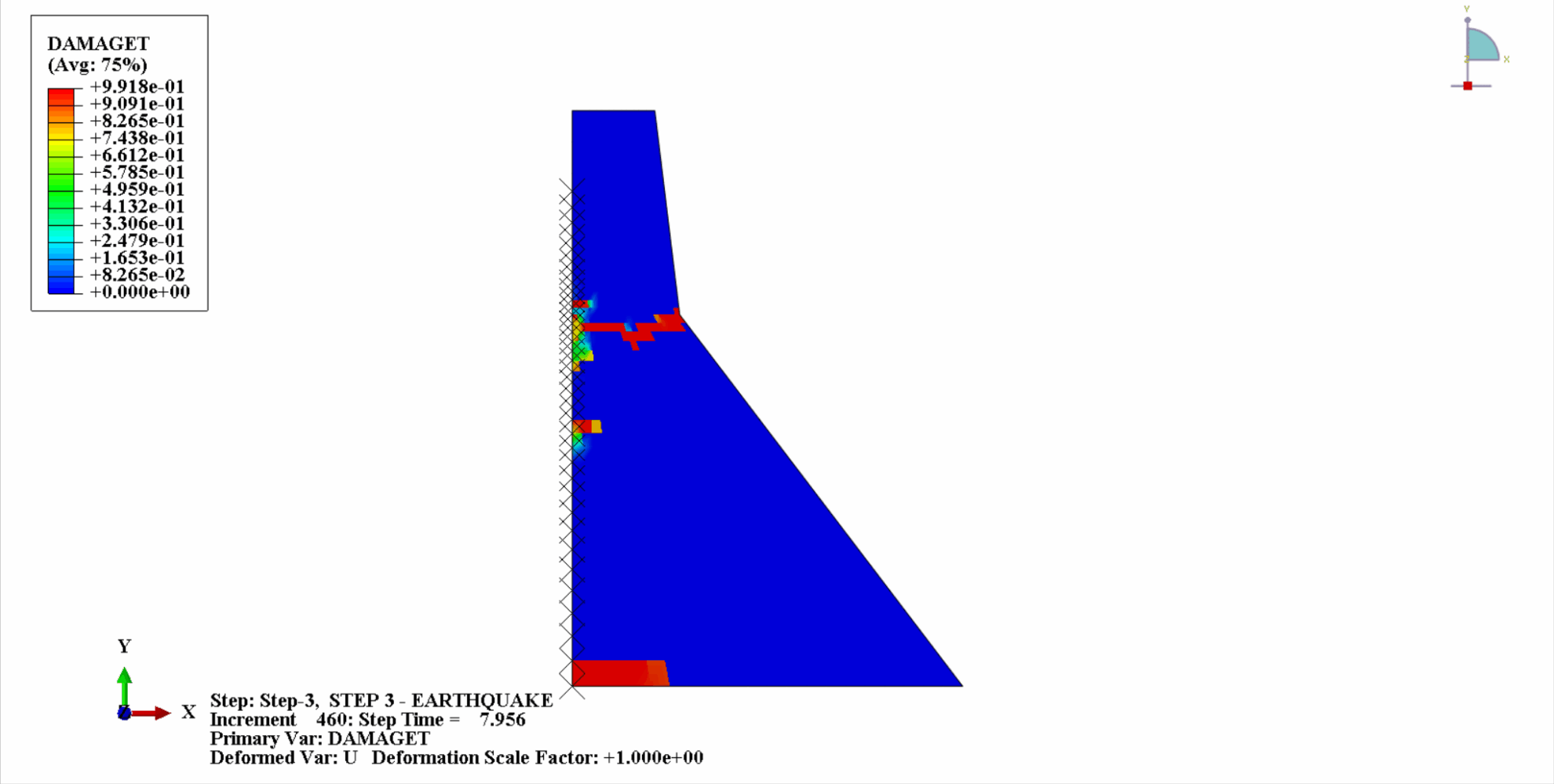
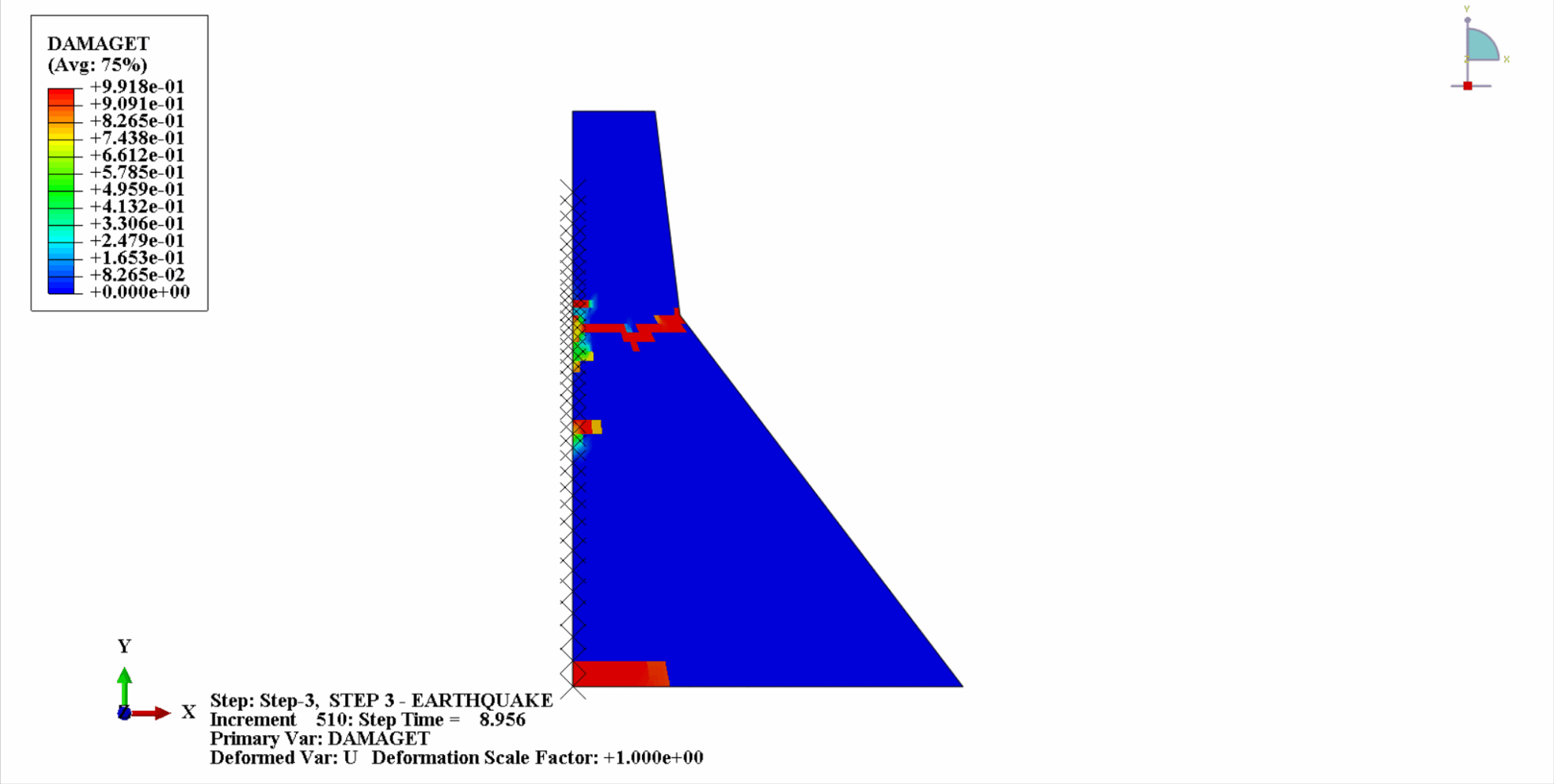
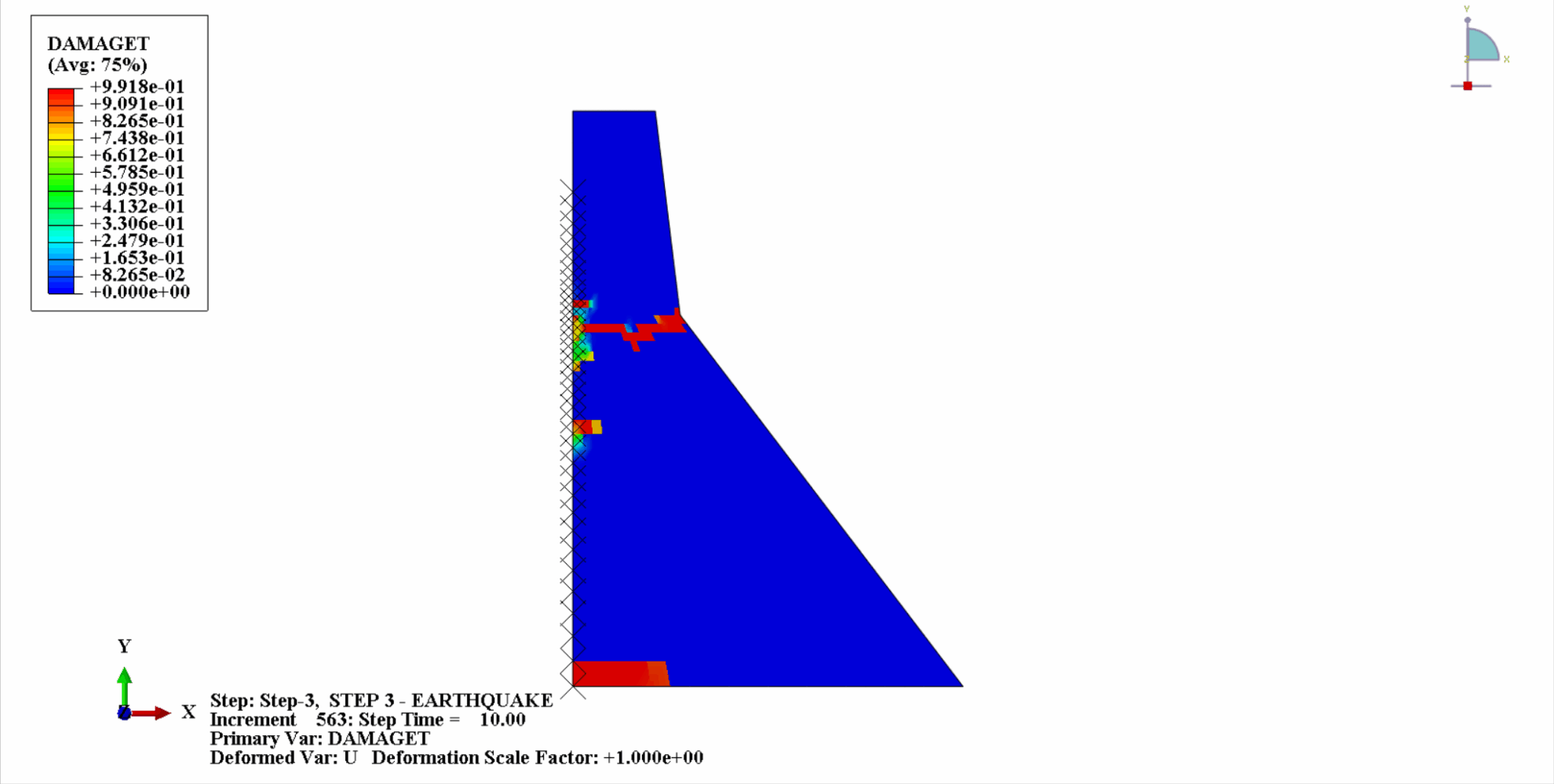
On peut constater qu’avec le temps, les dommages dus à la traction du béton du barrage s’accumulent progressivement. Au dernier moment du tremblement de terre, les dégâts atteignent leur maximum. La zone de dommage par traction du barrage en béton est principalement concentrée au centre du barrage et sur les pentes de pliage en amont et en aval du corps du barrage.