One-sentence Summary

Researchers from Shanghai AI Laboratory, Shanghai Jiao Tong University, and Peking University et al. propose InternGeometry, a medalist-level LLM agent for geometry that iteratively generates and verifies propositions using a symbolic engine, guided by a dynamic memory mechanism and trained with Complexity-Boosting Reinforcement Learning, solving 44 of 50 IMO problems with minimal data and outperforming AlphaGeometry 2 in efficiency.

Key Contributions

• InternGeometry addresses the challenge of weak heuristics in AI-driven geometry problem solving by enabling long-horizon interactions between an LLM and a symbolic engine, where the model iteratively proposes propositions and auxiliary constructions, verifies them formally, and uses feedback to guide future steps.
• The method introduces a dynamic memory mechanism to maintain and compress interaction history, allowing over 200 reasoning steps per problem, and employs Complexity-Boosting Reinforcement Learning (CBRL), a curriculum learning strategy that progressively increases problem difficulty during training to improve convergence and generalization.
• Evaluated on 50 IMO geometry problems (2000–2024), InternGeometry solves 44, exceeding the average gold medalist score (40.9) and prior systems like AlphaGeometry2 (42) and SeedGeometry (43), using only 13K training examples—just 0.004% of AlphaGeometry2's data—while also generating novel, human-unseen auxiliary constructions.

Introduction

The authors leverage large language model (LLM) agents to tackle International Mathematical Olympiad (IMO)-level geometry problems, a domain where performance has been dominated by expert systems like AlphaGeometry 2 that rely on massive synthetic datasets and extensive search. Geometry problems pose unique challenges due to the need for creative auxiliary constructions and long proof chains, which are difficult to model with standard heuristics or short-horizon reasoning. Prior LLM-based approaches have underperformed in this area, often limited to elementary problems or constrained by weak integration with symbolic reasoning tools.

To address these limitations, the authors introduce InternGeometry, an LLM agent that achieves medalist-level performance through iterative interaction with a symbolic engine. The agent proposes propositions and auxiliary constructions in natural language, verifies them formally, and reflects on feedback over hundreds of reasoning steps, guided by a dynamic memory mechanism that preserves critical information across turns. This long-horizon, trial-and-error reasoning mimics expert human strategies and enables the discovery of non-trivial proofs.

The key innovation is Complexity-Boosting Reinforcement Learning (CBRL), a curriculum learning framework that progressively increases the difficulty of synthetically generated training problems based on the agent’s current capability. This staged approach ensures stable policy learning and strong generalization, allowing InternGeometry to solve 44 of 50 IMO geometry problems (2000–2024), exceeding the average gold medalist score (40.9) with only 13K training examples—just 0.004% of the data used by AlphaGeometry 2. Notably, the model can generate novel auxiliary constructions not seen in human solutions, demonstrating emergent creativity in geometric reasoning.

Method

The authors leverage a tightly coupled architecture comprising an interactive geometric proof engine and a reasoning agent, designed to handle the long-horizon, multi-step nature of geometric theorem proving. The system operates through iterative cycles of natural-language reasoning, formal action execution, and environment feedback, with dynamic memory management enabling scalable interaction over hundreds of steps.

At the core of the framework is the InternGeometry-DDAR engine, which extends the open-source Newclid system with enhanced capabilities for global geometric constraint satisfaction, double-point handling, and integration of advanced theorems such as Power of a Point and Menelaus’ theorem. The engine maintains state across steps, including constructed auxiliary points, proven propositions, and geometric relationships. It executes actions issued by the agent—such as constructing points, circles, or lines, or proposing and verifying propositions—and returns structured feedback indicating success or failure. This feedback is critical for guiding the agent’s next reasoning step.

The geometric proof agent, denoted $\mathbb{G}$G, operates in a stepwise fashion. At each step $t$t, given the problem $X$X and a compressed history $\mathfrak{W}(H_{t-1})$W(Ht−1​), the agent outputs a pair $[P_t, A_t]$[Pt​,At​], where $P_t$Pt​ is a natural-language chain-of-thought and $A_t$At​ is a formalized action in domain-specific language (DSL). The action $A_t$At​ is executed by the engine $\mathbb{E}$E, which returns an observation $O_t$Ot​ and updates its internal state. The interaction history is then augmented as $H_t = H_{t-1} + [P_t, A_t, O_t]$Ht​=Ht−1​+[Pt​,At​,Ot​], forming the basis for subsequent reasoning.

To manage the exponential growth of interaction history, the authors introduce a memory manager $\mathfrak{W}$W that compresses earlier exchanges while preserving core actions and key feedback. This allows the agent to retain awareness of critical outcomes—such as whether an auxiliary construction succeeded or a proposition was proven—without being overwhelmed by verbose historical context. As shown in the framework diagram, this compressed history is fed back into the agent at each step, enabling long-horizon planning and reducing context inefficiency.

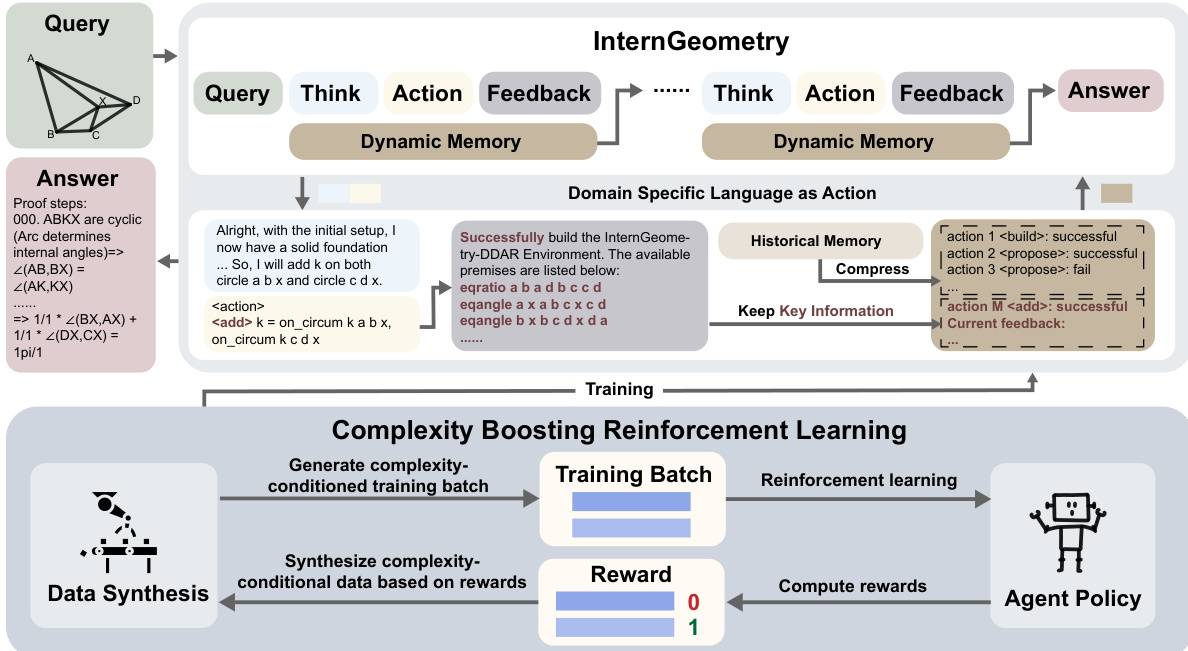
To mitigate action collapse—where the agent falls into repetitive or degenerate output patterns—the authors implement a prior-guided rejection sampling mechanism. During inference, candidate outputs $[\hat{P}_t, \hat{A}_t]$[P^t​,A^t​] are evaluated by a rule-based PassCheck policy that enforces diversity, validity, and action variety. Outputs violating these constraints are rejected and resampled, ensuring the agent maintains productive exploration throughout the proof process.

Training proceeds in two phases. First, supervised fine-tuning is performed on a synthetic dataset $\mathcal{D} = \{(X^i, h^i, y^i)\}_{i=1}^N$D={(Xi,hi,yi)}i=1N​, where $h^i = \mathfrak{W}(H^i)$hi=W(Hi) and $y^i = [P^i, A^i]$yi=[Pi,Ai]. The objective minimizes the negative log-likelihood of the agent’s outputs given the input and compressed history:

This phase instills foundational behaviors such as structured thinking and tool invocation.

The second phase employs Complexity Boosting Reinforcement Learning (CBRL), an iterative curriculum-driven RL loop. In each iteration, the agent attempts proofs on complexity-conditioned tasks sampled from a data synthesis pipeline $\mathfrak{X}(\kappa)$X(κ), where $\kappa$κ denotes the DDAR proof step count—a proxy for problem difficulty. The agent’s policy is updated using a GRPO-style objective that incorporates clipped policy ratios and KL regularization:

The reward $r$r is binary: $r = r^o \wedge r^s$r=ro∧rs, where $r^o = 1$ro=1 if the proof is complete, and $r^s = 1$rs=1 if the step’s action was effective (e.g., a proposed proposition was proven or an auxiliary construction was successfully used in the final proof). The advantage $A(X, y_t)$A(X,yt​) is normalized across trajectories to measure relative step quality.

Crucially, CBRL dynamically adjusts $\kappa$κ to maintain an average reward near 0.5, which maximizes the expected absolute advantage and thus accelerates learning. This is grounded in the observation that for binary rewards, the expected absolute advantage $2\sqrt{p(1-p)}$2p(1−p)​ is maximized at $p=0.5$p=0.5. The data synthesis pipeline generates nontrivial problems by sampling raw structures, augmenting them with auxiliary constructions, and selecting conclusions provable only with those additions—ensuring the training data is both challenging and solvable.

The entire system is trained end-to-end, with the agent policy continuously refined through interaction with the symbolic engine and feedback from the reward signal, enabling it to master complex geometric reasoning through iterative, curriculum-guided exploration.

Experiment

InternGeometry's reasoning style and larger model indeed increase computation. Each InternGeometry step involves natural-language reasoning, resulting in more tokens and higher compute: for IMO-50, the average number of output tokens per trajectory is 89.6K. The InternGeometry model (32B) is also larger than AlphaGeometry 2 (3.3B). Due to the unknown total cost of AlphaGeometry 2, a direct comparison is difficult. However, we emphasize that the increased computation from deeper reasoning and larger models should not be viewed as a drawback. Instead, it represents a feasible new scaling dimension—alongside training data size and the number of searched solutions—one that aligns more naturally with LLM-based approaches than with expert-model diagram."

InternGeometry, an LLM agent, solves 44 out of 50 IMO geometry problems using only 13K training samples, outperforming AlphaGeometry 2 and SeedGeometry despite using orders of magnitude less data. Its Pass@256 sampling setting achieves this result with a significantly smaller training dataset compared to the expert models, which rely on hundreds of millions of data points. The results highlight the efficiency of LLM-based agents in expert-level geometric reasoning when paired with targeted data synthesis and test-time scaling.

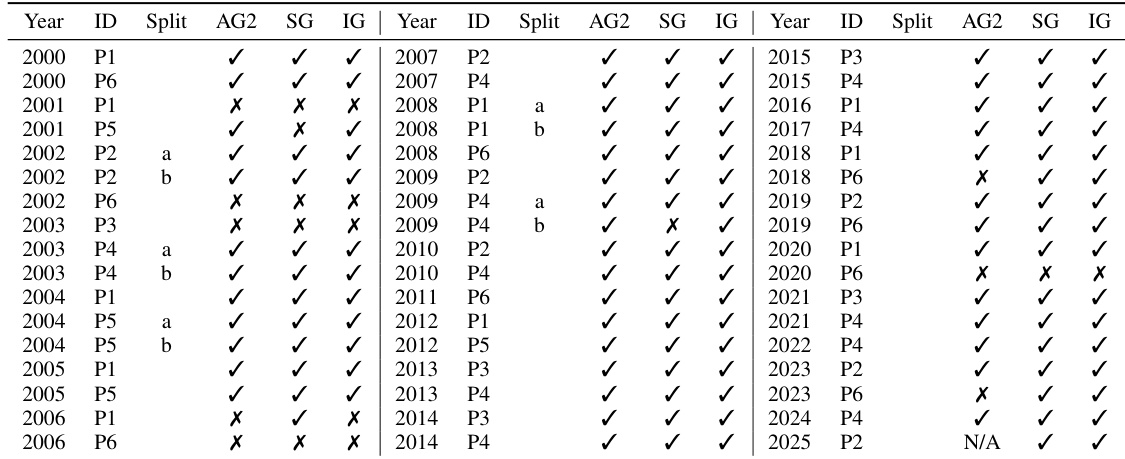
InternGeometry solved 44 out of 50 IMO geometry problems, outperforming AlphaGeometry 2 and SeedGeometry on this benchmark. It additionally solved two problems missed by both prior models—2018 P6 and 2023 P6—while only failing on three problems, two of which involve non-geometric computation beyond the current system’s scope. The model achieved this with significantly less training data and a more efficient inference budget compared to expert models.

The authors use ablation studies to evaluate the contribution of each long-horizon agent component in InternGeometry, showing that removing any of Propositions, Slow Thinking, Context Compression, or Reject Sampling reduces performance on IMO 50. Results show that all four components are critical, with the full configuration solving 44 out of 50 problems, while removing any single component drops performance by at least 6 problems. Slow Thinking and Context Compression have the largest individual impact, each contributing more than 10 additional solved problems when included.

Results show that InternGeometry achieves 44/50 on IMO 50 when trained with CBRL, significantly outperforming the 22/50 baseline from supervised fine-tuning alone. Using only easy or only challenging data during reinforcement learning yields lower performance at 29/50 and 24/50 respectively, while removing the dynamic difficulty schedule reduces performance to 38/50, confirming the importance of curriculum-based reinforcement learning.