Summarization

Researchers from Université Grenoble Alpes, New York University, and Genentech introduce MIST, a fully data-driven mutual information estimator trained on synthetic meta-datasets that utilizes quantile regression to provide calibrated uncertainty intervals, offering a differentiable and highly efficient alternative to classical baselines that relies on empirical generalization rather than theoretical guarantees.

Introduction

Mutual Information (MI) is a critical metric in data science for quantifying nonlinear dependencies between variables, serving as a cornerstone for tasks such as feature selection, representation learning, and causality. Because the true probability distributions of real-world data are rarely known, practitioners rely on estimators to infer MI from finite samples. However, existing techniques—whether they estimate data densities directly or approximate density ratios—often struggle in challenging, realistic settings. These methods tend to fail when dealing with high-dimensional data, limited sample sizes, or complex distributions, and they are frequently validated only on simple, low-MI Gaussian benchmarks that mask these performance gaps.

To overcome these limitations, the authors introduce MIST (Mutual Information estimation via Supervised Training), a framework that reframes MI estimation as a supervised learning problem rather than a mathematical derivation. Instead of approximating density functions during inference, the authors train a neural network end-to-end using a massive meta-dataset of synthetic distributions with known ground-truth MI values. This allows the model to learn the mapping from data samples to information content directly.

Key innovations and advantages of this approach include:

• Robustness in Low-Data Regimes: The estimator significantly outperforms existing baselines in difficult settings, providing reliable estimates with as few as 10 to 500 samples and across higher dimensions.
• Computational Efficiency: By amortizing the computational cost during training, the model performs inference orders of magnitude faster than prior neural methods, requiring only a single forward pass.
• Calibrated Uncertainty: The architecture incorporates quantile regression to provide built-in, well-calibrated confidence intervals, offering reliability that standard point-estimate methods lack.

Dataset

The authors construct a synthetic meta-dataset using the BMI library to enable supervised learning over distributions with known Mutual Information (MI). The dataset is organized as follows:

• Dataset Composition and Sources The meta-dataset consists of synthetic distributions generated via invertible transformations applied to base families with analytical MI. Each entry, or "meta-sample," pairs joint samples from a specific distribution with its ground-truth MI value.

• Distribution Categories The data is categorized into two main groups based on their relationship to the training data:

  • In-Meta-Distribution (IMD): This subset includes base distributions such as Multivariate Normal (with dense or latent variable model variants) and Multivariate Student’s t-distributions (with dense or sparse structures). These families share covariance structures but differ in tail heaviness and parameterization.
  • Out-of-Meta-Distribution (OoMD): This subset contains distribution families entirely absent from the training set to test generalization. It features a multivariate additive noise model characterized by non-Gaussian properties and bounded support, where noise is controlled by a shared scale parameter.

• Data Partitioning and Usage To promote diversity, the authors partition distribution families into disjoint training and testing groups. For evaluation, they construct two distinct corpora:

  • Standard Benchmark: A smaller test set designed for comparison with existing, computationally intensive estimators.
  • Extended Benchmark: A larger test set used to assess generalization to novel distributions and higher dimensions.

• Processing and Metadata

  • Dimensionality: The sample dimensionality across the dataset varies from 2 to 32.
  • Ground Truth: True MI values are computed either analytically or numerically depending on the tractability of the specific distribution family.
  • Parameter Sampling: Hyperparameters for structure (such as correlation, latent signal strength, and degrees of freedom) are sampled from specific uniform distributions to ensure variety within each family.

Method

The authors propose a fully data-driven framework for mutual information estimation, reimagining the problem as a supervised learning task where a model learns to predict mutual information directly from finite samples. This approach, termed MIST (Mutual Information estimation from Supervised Training), bypasses traditional density estimation or ratio approximation methods by training a neural network to map a set of paired samples $\{(x_i, y_i)\}_{i=1}^n${(xi​,yi​)}i=1n​ to an estimate of $I(X;Y)$I(X;Y). The model is trained end-to-end on a large meta-dataset of synthetic joint distributions, where each training example consists of a dataset of samples and its corresponding ground-truth mutual information value. The learning objective is to minimize the mean squared error between the predicted MI and the true MI, effectively training the model to approximate the Bayes-optimal regression function that outputs the posterior expectation of MI given the observed data.

As shown in the figure below, the framework consists of two main components: a synthetic meta-dataset and a supervised prediction model. The meta-dataset is constructed by sampling from a diverse family of joint distributions, each with a known mutual information value, and generating finite datasets of varying sizes and dimensions. The prediction model, MIST, is designed to process these variable-sized datasets while being invariant to the order of samples. The model architecture is based on the SetTransformer++ framework, which is well-suited for processing unordered sets of data. The core of the architecture is a series of ISAB (Intra-Set Attention Block) layers that perform attention over a fixed number of learned inducing points, enabling efficient processing of variable-length inputs. To handle variable input dimensions, an additional row-wide attention block is introduced, which operates along the feature axis and uses a learned pooling mechanism to reduce the dimensionality to a fixed size. This row pooling step ensures that the model can process inputs of different dimensionalities. The processed features are then passed through a final MLP (Multi-Layer Perceptron) to produce the MI prediction. The model can be trained to predict a point estimate of MI using a mean squared error loss, or to predict quantiles of the MI distribution using a pinball loss, enabling built-in uncertainty quantification. The framework is designed to be robust to the wide range of MI values encountered in practice, with the authors finding that direct prediction of MI yields the best performance, provided the meta-dataset includes a sufficient range of MI labels.

Experiment

• Benchmarking against existing methods on synthetic distributions validated that the learned estimators outperform baselines, achieving approximately 10x lower error on seen distributions and 5x lower error on unseen distributions.
• In high-dimensional and low-sample regimes, the models demonstrated up to 100x lower loss than the KSG baseline and avoided the negative bias typically associated with estimating large Mutual Information values.
• Scaling and efficiency experiments showed the method requires roughly half the samples of the best baseline for reliable estimates and performs inference 4 to 80 times faster than KSG.
• Uncertainty quantification analysis confirmed that quantile-based intervals are well-calibrated, yielding approximately 2x better coverage than KSG across tested settings.
• Generalization studies indicated robust performance on unseen distributions and sample sizes, though accuracy decreases when simultaneously encountering unseen distributions and higher dimensionalities.
• Variable dimension experiments revealed that training on a diverse mix of dimensions reduces Mean Squared Error by 2 to 3 times for high-dimensional data ($D \ge 16$D≥16) compared to specialized single-dimension models.

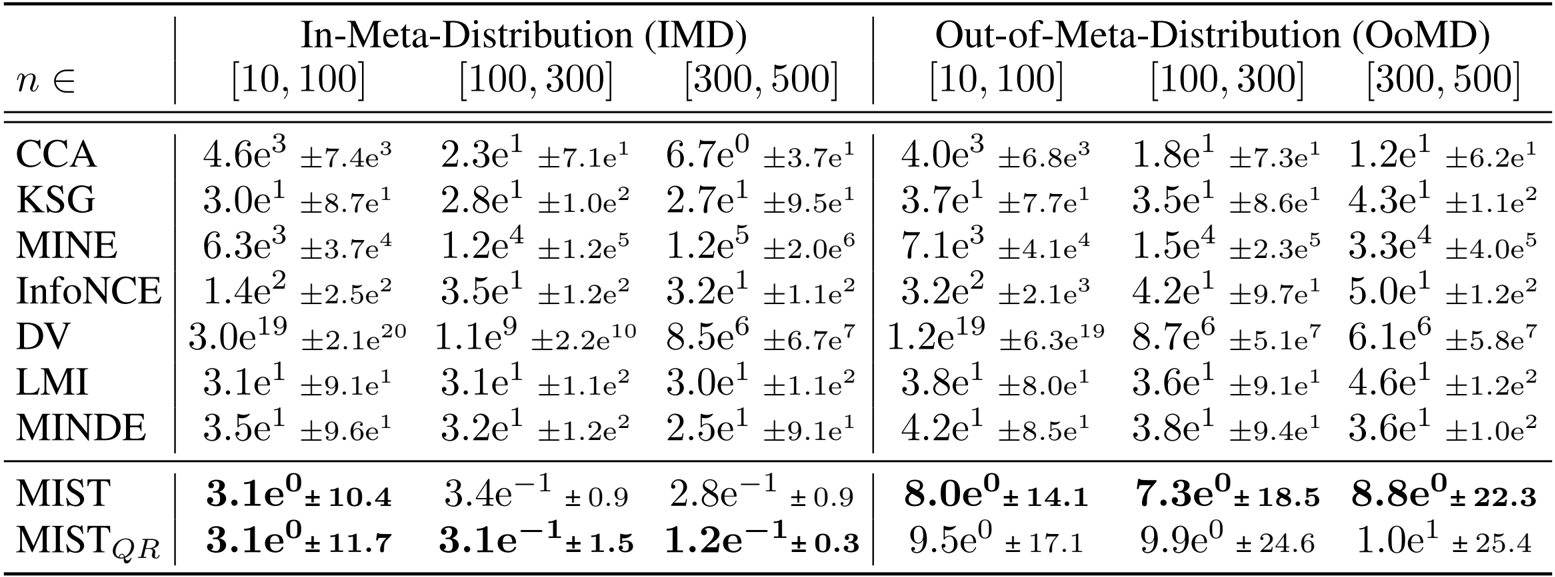
The authors use the table to compare the performance of their learned estimators, MIST and MIST_QR, against several existing methods across different sample sizes and distribution types. Results show that MIST and MIST_QR achieve significantly lower mean squared error than all baselines, particularly in low-sample and high-dimensional settings, with MIST_QR demonstrating superior calibration and reliability in uncertainty estimation.