Notions De Base Sur Les Réseaux Neuronaux : Algorithme De Rétropropagation

Geoffrey Hinton

Geoffrey Hinton est un informaticien et psychologue canadien d'origine britannique qui a apporté de nombreuses contributions au domaine des réseaux neuronaux. Il est l’un des inventeurs de l’algorithme de rétropropagation et un promoteur actif de l’apprentissage profond. Il est connu comme le père des réseaux neuronaux et de l’apprentissage profond.

De plus, Hinton est le fondateur du Gatsby Centre for Computational Neuroscience de l'Université de Londres et est actuellement professeur au Département d'informatique de l'Université de Toronto, au Canada. Ses principaux intérêts de recherche portent sur l’application des réseaux de neurones artificiels à l’apprentissage automatique, à la mémoire, à la perception et au traitement des symboles. Actuellement, Hinton étudie comment appliquer les réseaux neuronaux aux algorithmes d’apprentissage non supervisé.

Cependant, parmi les nombreux résultats de recherche scientifique de Hinton, la rétropropagation est la plus célèbre et constitue la base de la plupart des algorithmes actuels de réseaux neuronaux d'apprentissage supervisé, qui reposent sur la méthode de descente de gradient. Son principe de fonctionnement principal est :

En fonctionnement réel, l'algorithme ANN est généralement divisé en trois catégories : couche d'entrée, couche cachée et couche de sortie. Lorsqu'il y a une erreur entre le résultat de sortie de l'algorithme et le résultat cible, l'algorithme calcule la valeur d'erreur, puis renvoie la valeur d'erreur à la couche cachée via la rétropropagation, l'ajuste en modifiant les paramètres pertinents et répète cette étape jusqu'à ce que le résultat attendu soit obtenu.

La rétropropagation permet à l’algorithme ANN d’obtenir des résultats plus proches de la cible. Cependant, avant de comprendre comment la rétropropagation est appliquée à l’algorithme ANN, il est nécessaire de comprendre d’abord le principe de fonctionnement de l’ANN.

L'ANN est un modèle mathématique ou un modèle informatique basé sur le réseau neuronal du cerveau humain, qui est composé d'un grand nombre de nœuds (qui peuvent être compris comme des neurones biologiques) connectés les uns aux autres.

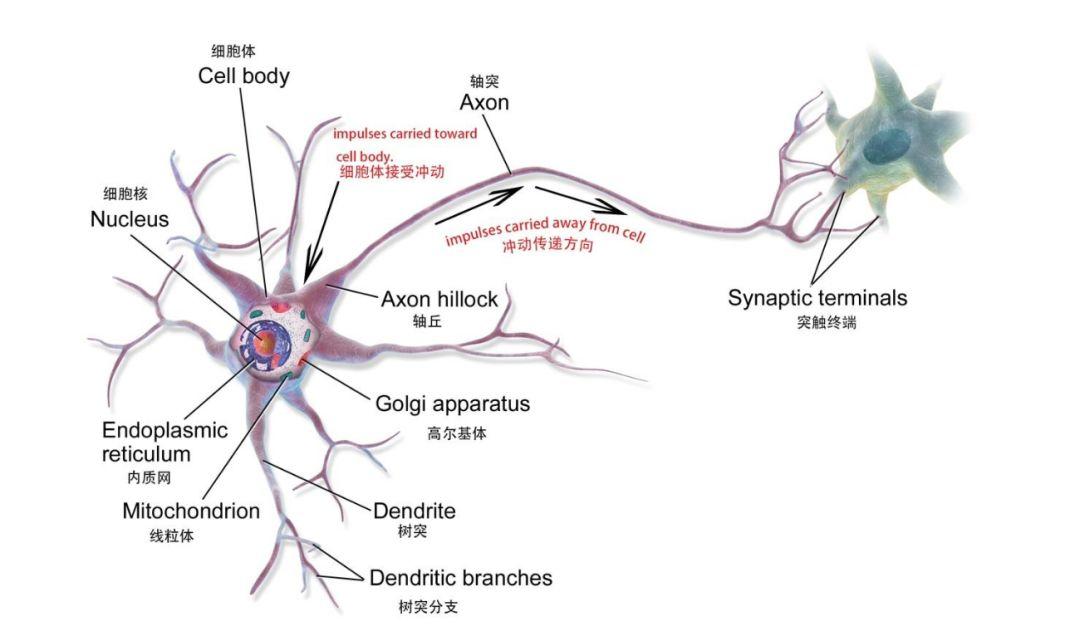
Neurones biologiques

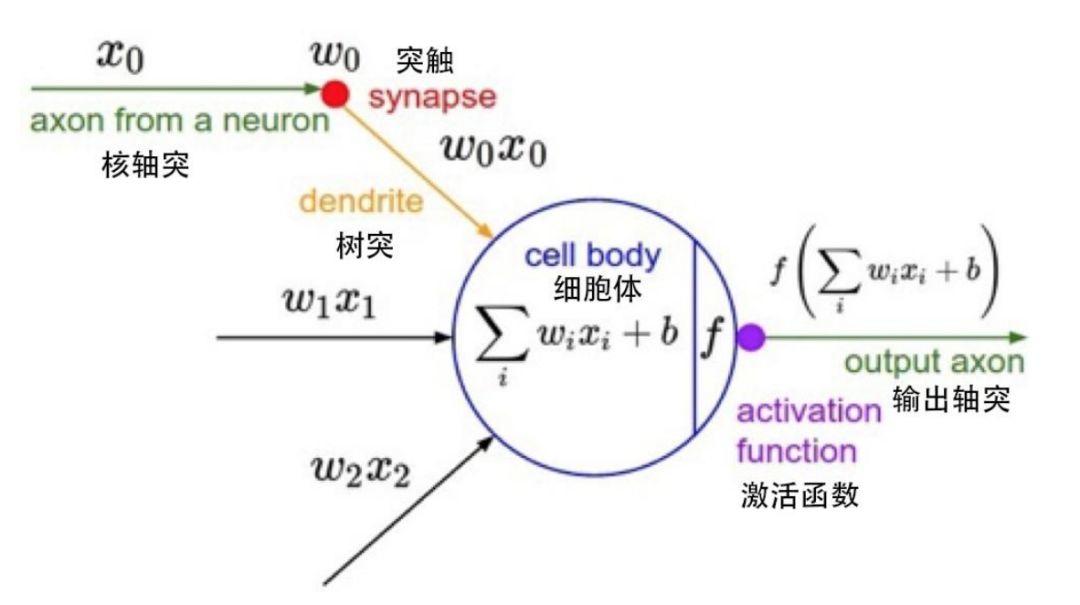
Un seul nœud dans un modèle mathématique

Chaque nœud représente une fonction de sortie spécifique, appelée fonction d’activation ; la connexion entre deux nœuds représente une valeur pondérée, également appelée valeur de pondération. Lors du fonctionnement de l'algorithme ANN, chaque connexion correspond à un poids w et à un décalage b (également appelés paramètres ANN). La valeur de sortie est liée au nœud, au poids et au décalage.

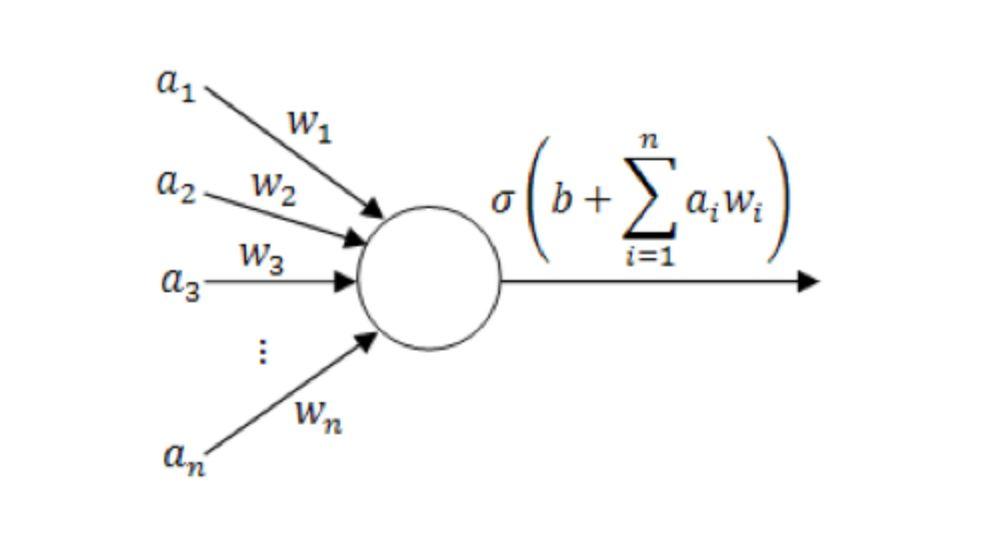
Diagramme du modèle de neurone unique

(où un1~unn sont les composantes du vecteur d'entrée ; w1~wn est la valeur de poids ; b est le décalage ; σ est la fonction d'activation, telle que tanh, Sigmoid, ReLU, etc.)

Un ANN complet se compose généralement d'une couche d'entrée, de plusieurs couches cachées et d'une couche de sortie. La couche cachée est principalement composée de neurones et effectue le travail de calcul le plus important. Au cours de l'opération proprement dite, les neurones de chaque couche prendront des décisions et transmettront les décisions aux neurones de la couche cachée suivante jusqu'à ce que le résultat final soit obtenu.

Par conséquent, plus il y a de couches cachées, plus le réseau de neurones artificiels est complexe et plus les résultats seront précis. Par exemple, si vous souhaitez utiliser un ANN pour déterminer si l'animal d'entrée est « un chat » ou « pas un chat », après avoir entré l'animal, les neurones de chaque couche cachée porteront un jugement sur celui-ci, obtiendront un résultat et transmettront le résultat vers le bas jusqu'à ce que la dernière couche de neurones génère le résultat.

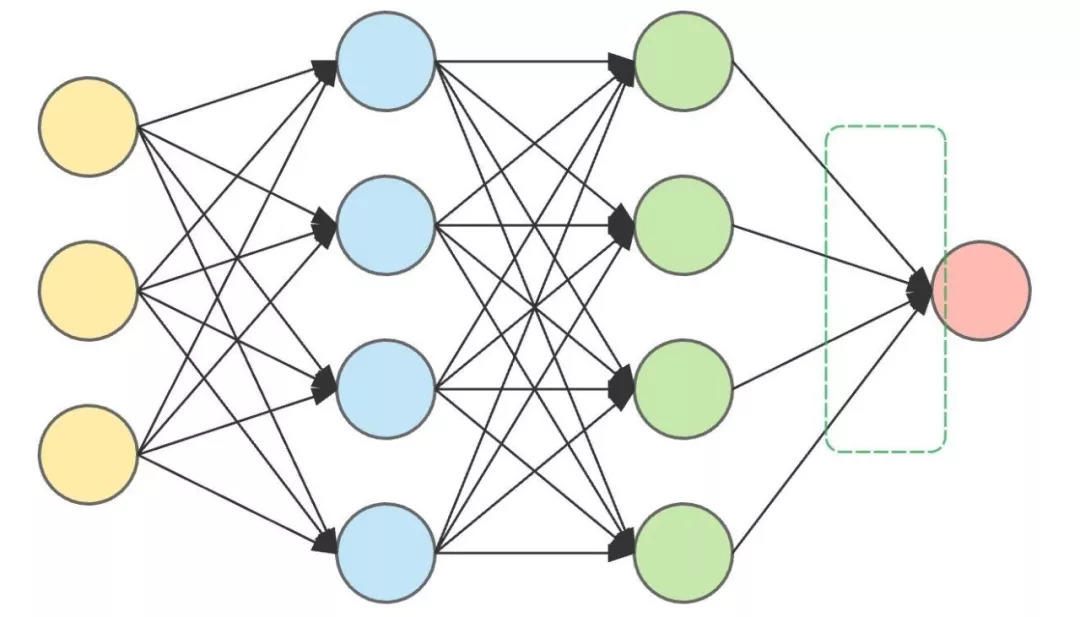
Il s’agit d’une architecture ANN avec deux couches cachées.

La couche d'entrée (à gauche) et la couche de sortie (à droite) se trouvent des deux côtés, et les deux couches cachées se trouvent au milieu.

Si l’animal est biologiquement un chat, mais que le réseau de neurones artificiels indique qu’il « n’est pas un chat », alors la sortie du réseau de neurones artificiels est erronée. Maintenant, la seule chose que nous pouvons faire est de revenir à la couche cachée et d’ajuster les poids et les biais, et ce processus de retour en arrière et d’ajustement des données est la rétropropagation.

Cependant, pour réaliser la rétropropagation, nous devons également nous appuyer sur un type d’algorithme important : l’algorithme de descente de gradient. La descente de gradient accélère considérablement le processus d’apprentissage. Cela peut être simplement compris comme suit : lorsque l'on descend la montagne depuis le sommet, choisir le chemin avec la pente la plus raide est le plus rapide.

Étant donné que nous devons constamment calculer l’écart entre la sortie et la valeur réelle pour modifier les paramètres (plus la différence est grande, plus la modification est importante), nous devons utiliser une fonction d’erreur (également appelée fonction de perte) pour mesurer l’erreur entre la valeur prédite finale et la valeur réelle de tous les échantillons de l’ensemble d’apprentissage.

dans y^i est le résultat de la prédiction, yje Pour des résultats réels.

Cette expression mesure l'erreur entre la valeur prédite finale et la valeur réelle de tous les échantillons de l'ensemble d'apprentissage, qui n'est liée qu'à la catégorie prédite de la couche de sortie, mais cette valeur prédite dépend des paramètres des couches précédentes. Si nous ne voulons pas classer les chiens comme des chats, nous devons minimiser cette fonction d’erreur.

L'algorithme de descente de gradient est l'un des algorithmes qui minimise la fonction d'erreur. Il s’agit également d’un algorithme d’optimisation couramment utilisé dans la formation des modèles ANN. La plupart des modèles d’apprentissage en profondeur utilisent l’algorithme de descente de gradient pour la formation à l’optimisation. Étant donné un ensemble de paramètres de fonction, la descente du gradient commence à partir d'un ensemble initial de valeurs de paramètres et se déplace de manière itérative vers un ensemble de valeurs de paramètres qui minimise la fonction de perte. Cette minimisation itérative est implémentée à l'aide du calcul, en prenant les changements de gradient dans la direction négative du gradient. L’exemple classique d’utilisation de la descente de gradient est la régression linéaire. Au fur et à mesure que le modèle s’exécute, la fonction de perte converge progressivement vers la valeur minimale.

Étant donné que le gradient exprime la direction du taux de variation maximal d'une fonction à un certain point et est obtenu en calculant la dérivée partielle, l'utilisation de la méthode de descente de gradient accélérera considérablement le processus d'apprentissage.

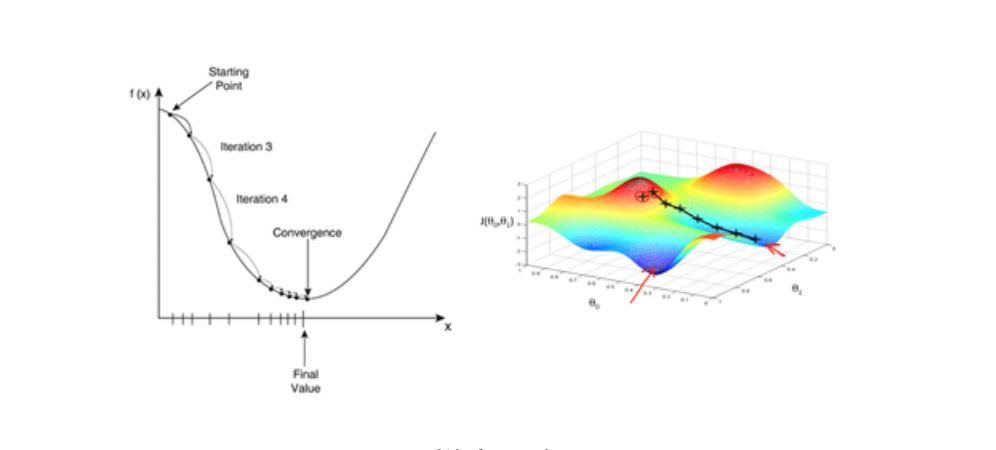
Descente de gradient

En pratique, il est théoriquement possible de vérifier d’abord comment les poids et les biais de la dernière couche affectent le résultat. En prenant la dérivée partielle de la fonction d'erreur E, nous pouvons voir l'impact des valeurs de poids et des décalages sur la fonction d'erreur.

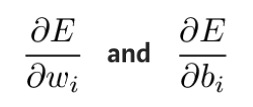
Ces dérivées partielles peuvent être calculées à l’aide de la règle de la chaîne pour découvrir comment les changements de ces paramètres affectent la sortie. La formule de dérivation est la suivante :

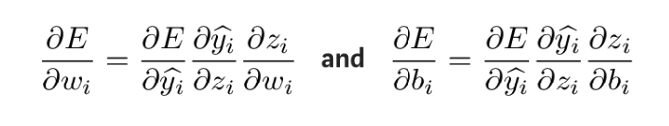
Pour obtenir la quantité inconnue dans l'expression ci-dessus, prenez la dérivée partielle de zi par rapport à wi et bi respectivement :

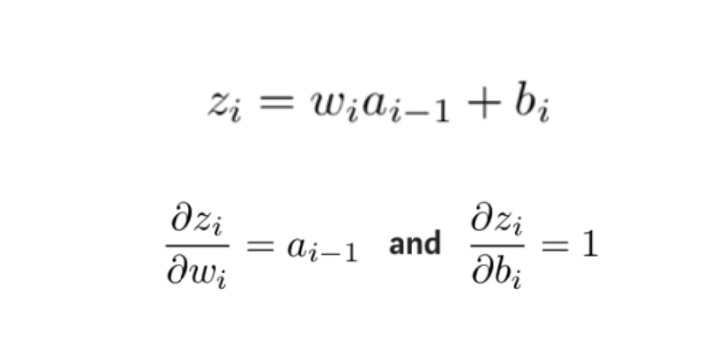Ensuite, les dérivées partielles de la fonction d'erreur par rapport aux poids et aux décalages de chaque couche sont calculées dans l'ordre inverse, et les poids et les décalages ajustés sont mis à jour par la méthode de descente de gradient jusqu'à la couche initiale où l'erreur se produit.

Ce processus est l'algorithme de rétropropagation, également connu sous le nom d'algorithme BP, qui propage l'erreur de la couche de sortie vers l'arrière couche par couche et met à jour les paramètres du réseau en calculant des dérivées partielles pour minimiser la fonction d'erreur, afin que l'algorithme ANN puisse obtenir la sortie attendue.

Actuellement, la rétropropagation est principalement utilisée dans les algorithmes ANN sous apprentissage supervisé.