Prédisez Avec Précision Les Prix De L'immobilier À Wuhan ! Le Laboratoire SIG De L'université Du Zhejiang a Proposé Le Modèle Osp-gnnwr : Décrivant Avec Précision Les Processus Spatiaux Complexes Et Les Phénomènes Géographiques

Le logement est un élément important du bien-être humain et du développement social, et les fluctuations des prix du logement ont fait l’objet d’une attention généralisée de la part de la société. La Chine est un pays avec une étendue géographique très vaste. Même dans la même juridiction de la même ville, les maisons dans différentes zones auront des prix de logement différents en raison des différences d'environnement communautaire, de districts scolaires, d'entreprises de soutien et d'autres facteurs. Par conséquent, l’un des sujets brûlants dans l’étude des prix de l’immobilier est sa différenciation spatiale et son mécanisme d’influence, ce qu’on appelle « l’hétérogénéité spatiale ».

Ces dernières années, les différences spatiales dans les prix des logements sont devenues de plus en plus importantes, et une seule méthode de mesure de distance est insuffisante pour saisir « l’hétérogénéité spatiale » des prix des logements dans un environnement géographique complexe. En particulier dans les grandes villes comme Wuhan, des facteurs tels que les caractéristiques naturelles (comme les rivières et les lacs) et les infrastructures urbaines (comme les ponts, les tunnels et les réseaux routiers à plusieurs niveaux) ont un impact complexe sur les prix des logements.Les modèles traditionnels de régression pondérée géographiquement (GWR) sont confrontés à des défis dans la mesure de la proximité spatiale.

Dans ce contexte, des chercheurs du laboratoire SIG de l'Université du Zhejiang ont publié un article de recherche intitulé « Un modèle de réseau neuronal pour optimiser la mesure de la proximité spatiale dans l'approche de régression géographiquement pondérée : une étude de cas sur le prix de l'immobilier à Wuhan » dans l'International Journal of Geographical Information Science, une revue bien connue dans le domaine des sciences de l'information géographique.

Cette étude a introduit de manière innovante une méthode de réseau neuronal pour effectuer un couplage non linéaire sur plusieurs mesures de proximité spatiale (telles que la distance euclidienne, le temps de trajet, etc.) entre les points d'observation pour obtenir une mesure de proximité spatiale optimisée (OSP), améliorant ainsi la précision de la prédiction du modèle des prix des logements.

Pour résoudre le problème selon lequel la « proximité spatiale » abstraite ne peut pas construire de fonctions de perte et les réseaux neuronaux sont difficiles à former,Cette étude combine en outre l'OSP avec la méthode de régression pondérée par réseau neuronal géographique (GNNWR).Le modèle osp-GNNWR a été construit pour réaliser la formation du réseau neuronal en résolvant la relation de régression spatiale non stationnaire entre les variables dépendantes et les variables indépendantes.

Points saillants de la recherche :

• En introduisant une mesure de proximité spatiale optimisée et en l'intégrant dans l'architecture du réseau neuronal, l'applicabilité de la régression pondérée géographiquement dans l'étude de la distribution spatiale des processus géographiques tels que les prix des logements est efficacement améliorée.
• Grâce à l’étude d’ensembles de données simulées et de cas empiriques de prix de l’immobilier à Wuhan, le modèle proposé dans l’article s’avère avoir de meilleures performances globales et peut décrire plus précisément des processus spatiaux complexes et des phénomènes géographiques.
• Cela ouvre de nouvelles perspectives pour étudier comment personnaliser les mesures de proximité spatiale afin d'améliorer les performances de divers modèles de régression géospatiale.

Adresse du document :
https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2343771

Le projet open source « awesome-ai4s » rassemble plus de 100 interprétations d'articles AI4S et fournit également des ensembles de données et des outils massifs :

https://github.com/hyperai/awesome-ai4s

Ensemble de données : Wuhan est utilisé comme zone de recherche typique

Ensemble de données simulées

Pour évaluer la précision d’ajustement du modèle osp-GNNWR, les chercheurs ont généré un ensemble de données simulées spatialement hétérogènes 64 × 64. L'hétérogénéité spatiale de l'ensemble de données simulées ne se reflète pas seulement dans la distance en ligne droite, mais montre également les caractéristiques de distribution spatiale définies par la distance non euclidienne, ce qui peut démontrer l'efficacité de l'OSP.

Ensemble de données réel

Wuhan, capitale de la province du Hubei, est située dans le centre de la Chine, au confluent du fleuve Han et du fleuve Yangtze. Wuhan a un climat subtropical humide avec des précipitations abondantes et de nombreuses rivières, lacs et étangs, ce qui rend l’évaluation de la proximité spatiale difficile. En tant que ville la plus grande et la plus densément peuplée du centre de la Chine, Wuhan dispose également d’un marché immobilier florissant, fournissant de nombreuses données pour construire un modèle complet de la dynamique immobilière spécifique de Wuhan.

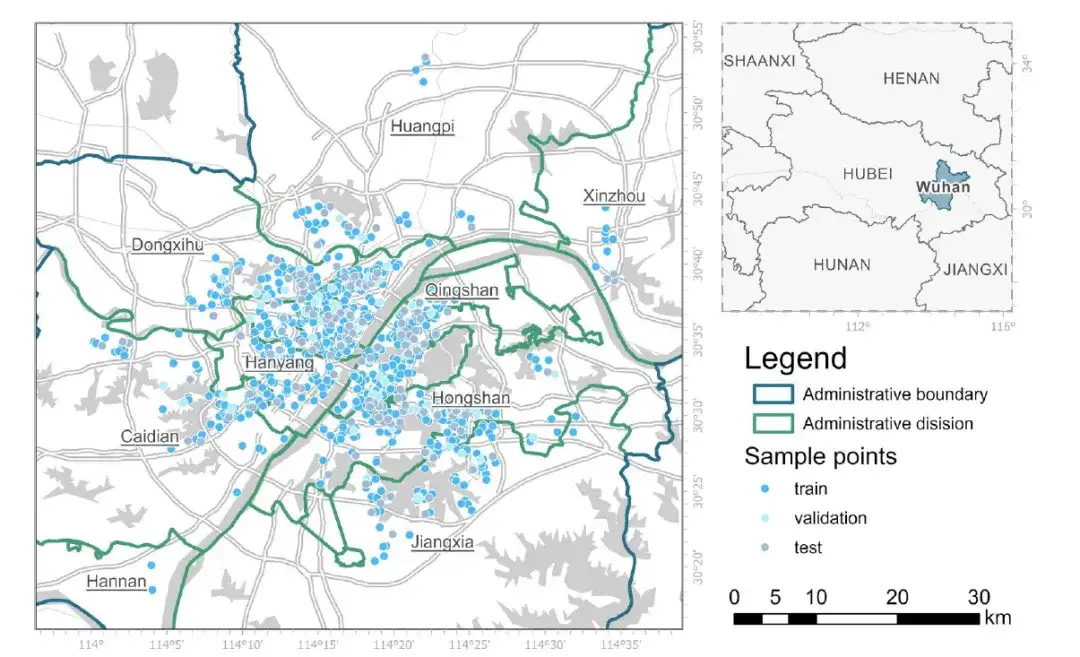
à cette fin,Les chercheurs ont compilé un ensemble de données contenant 968 échantillons immobiliers différents.Ces données proviennent des registres des transactions de logements d'occasion à Wuhan en 2019, et la source des données est Anjuke (https://wuhan.anjuke.com). Tous ces enregistrements ont été nettoyés, les types de propriétés particulières (comme les villas) ont été exclus et la qualité des données a été assurée.

Architecture du modèle : introduction d'une métrique de proximité spatiale optimisée et son intégration dans un réseau neuronal

La construction du modèle osp-GNNWR est divisée en deux étapes :

Étape 1 : Obtenir la mesure de proximité spatiale optimisée (OSP)

Afin d'obtenir une mesure de proximité spatiale plus précise dans une analyse géographique complexe, cette étude a intégré plusieurs méthodes de mesure de distance, notamment la distance euclidienne, la distance de Manhattan et le temps de trajet, pour optimiser la proximité spatiale (OSP). De cette manière, la mesure optimisée de la proximité spatiale peut mieux refléter les différents facteurs d’influence dans les relations spatiales complexes, améliorant ainsi l’ajustement et le pouvoir explicatif du modèle de régression spatiale.

Étape 2 : En combinant davantage l’OSP avec le GNNWR, les chercheurs ont proposé le modèle osp-GNNWR.Comme le montre la figure suivante :

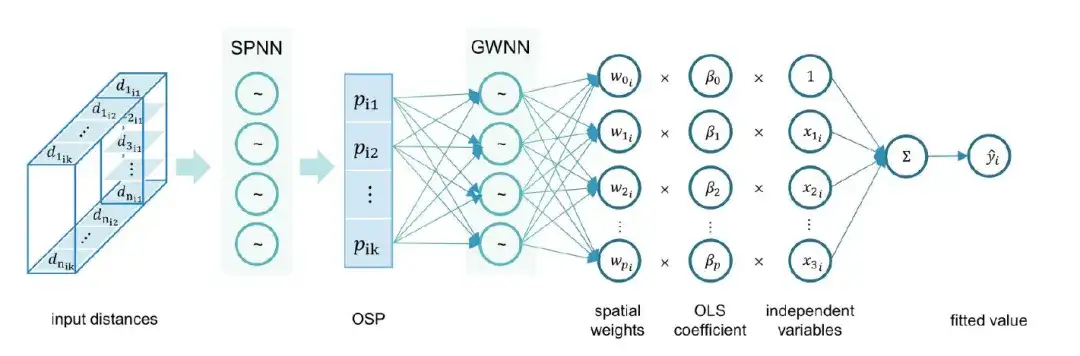
Plus précisément, les procédures de formation et de validation du modèle osp-GNNWR sont les suivantes :

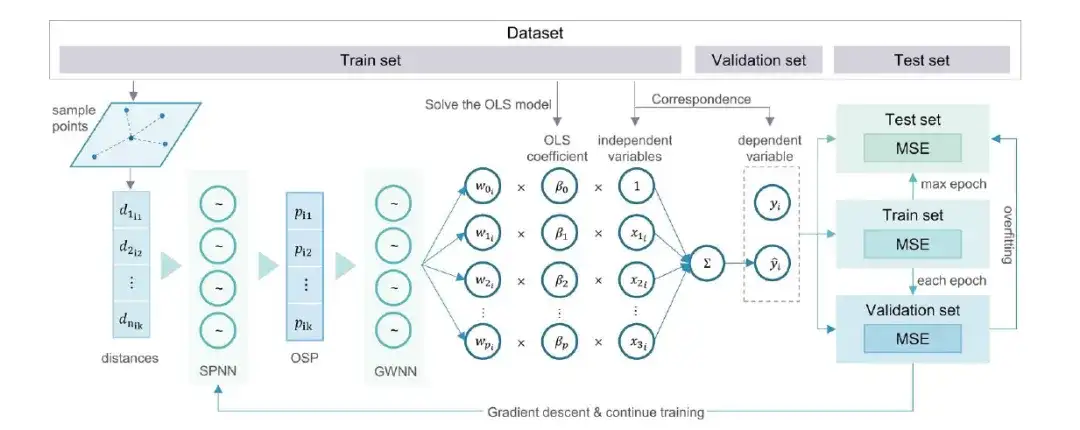
Étape 1 :Extraire des variables dépendantes et des variables indépendantes pour construire des modèles de régression ;

Étape 2 :L'ensemble de données est divisé aléatoirement en un ensemble d'apprentissage, un ensemble de validation et un ensemble de test dans des proportions appropriées ;

Étape 3 :Les distances d’échantillonnage sont calculées comme des informations spatiales dans le modèle osp-GNNWR ;

Étape 4 :À l’aide de variables d’entrée et d’informations spatiales, un modèle osp-GNNWR incluant la structure du réseau et les hyperparamètres est établi ;

Étape 5 :Obtenez des données par mini-lots à partir de l'ensemble d'entraînement, entraînez-vous à l'aide de l'algorithme de descente de gradient et évaluez la qualité de l'ajustement, par exemple en utilisant l'erreur quadratique moyenne (MSE) comme fonction de perte ;

Étape 6 :Évaluer si l’époque actuelle est terminée ; sinon, revenez à l'étape 5.

Étape 7 :Évaluer la fonction de perte sur l’ensemble de validation pour déterminer s’il y a surajustement ; si la perte est améliorée par rapport au meilleur résultat précédent, conserver le nouveau modèle supérieur ; sinon, augmentez le nombre de tolérances de surajustement ;

Étape 8 :Évaluer si la tolérance de surapprentissage ou le nombre maximal d’époques (époque maximale) a été atteint ; lorsque la limite est atteinte, l'entraînement s'arrête et l'ensemble de test est utilisé pour évaluer le dernier modèle supérieur ; sinon, continuez l'itération à partir de l'étape 5.

Grâce aux étapes ci-dessus, les chercheurs peuvent former et valider efficacement le modèle osp-GNNWR pour capturer et expliquer l’hétérogénéité des relations spatiales complexes et améliorer la précision et la fiabilité du modèle.

Résultats de recherche : le modèle osp-GNNWR a de meilleures performances globales

Commençons par examiner les résultats de l’analyse basée sur l’ensemble de données simulées. Sur un ensemble de données simulées basées sur la distance euclidienne et la distance d'ordre Z, les chercheurs ont utilisé des modèles incluant OLS, GWR, GNNWR et osp-GNNWR à des fins de comparaison. Les résultats sont présentés dans le tableau suivant :

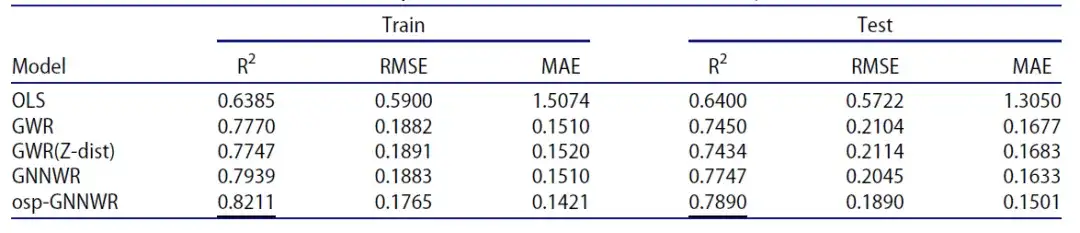
• R² : Mesure de la mesure dans laquelle la variation d'une variable (la variable dépendante) peut être expliquée par la variation d'une ou plusieurs autres variables (les variables indépendantes). Cette valeur est souvent utilisée dans l’analyse de régression linéaire pour évaluer la qualité de l’ajustement du modèle. 0% signifie que le modèle ne peut expliquer aucune variation de la variable de réponse autour de sa moyenne, c'est-à-dire qu'il n'y a presque aucune relation entre le modèle et les données ; 100% signifie que le modèle peut expliquer toute variation de la variable de réponse autour de sa moyenne, c'est-à-dire que le modèle s'adapte parfaitement aux données.
• RMSE (root mean square error) : Il est utilisé pour mesurer l'écart entre la valeur observée et la valeur vraie. Plus la valeur est petite, plus la précision de prédiction du modèle est élevée.
• MSE (erreur absolue moyenne) : utilisé pour mesurer l'écart absolu moyen entre la valeur prédite du modèle et la valeur réelle. Plus la valeur est petite, plus la précision de prédiction du modèle est élevée.

Que ce soit sur l'ensemble de données d'entraînement ou sur l'ensemble de données de test, le modèle osp-GNNWR a un R² plus élevé, une valeur RMSE plus faible et une valeur MSE plus faible, affichant ainsi de meilleures performances. Ces résultats expérimentaux de simulation démontrent que le réseau SPNN utilisé dans le modèle osp-GNNWR possède une excellente capacité de généralisation et un effet d'ajustement très précis lors du traitement des distances d'entrée. Par conséquent, par rapport à la méthode traditionnelle qui repose uniquement sur la distance euclidienne,Le modèle osp-GNNWR présente des avantages potentiels pour décrire l’hétérogénéité spatiale des processus géographiques du monde réel.

Le deuxième est la performance du modèle osp-GNNWR basé sur les données réelles des prix des logements à Wuhan. Le tableau suivant présente les résultats de comparaison des performances des modèles OLS, GWR, GNNWR et osp-GNNWR :

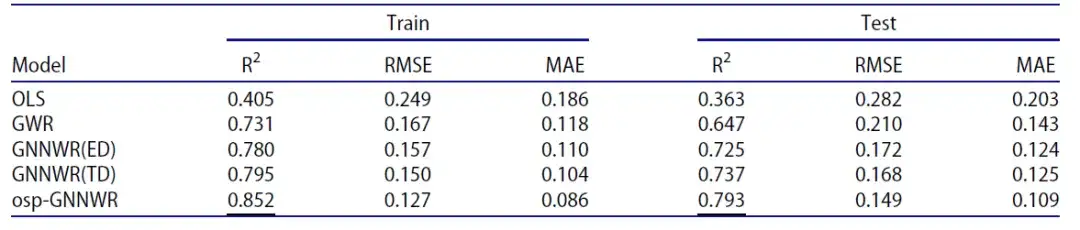
De même, le modèle osp-GNNWR présente un R² plus élevé, une valeur RMSE plus faible et une valeur MSE plus faible sur les ensembles de données d’entraînement et de test, affichant ainsi de meilleures performances.

Il convient de noter que par rapport au GNNWR(TD), le modèle osp-GNNWR améliore le R² de l'ensemble de données de test de 0,737 à 0,793, et réduit le RMSE de 0,168 à 0,149 et le MAE de 0,125 à 0,109. Ces résultats indiquent queL'intégration d'OSP améliore les performances d'ajustement et de prédiction du modèle osp-GNNWR.ce qui en fait l’approche la plus efficace parmi les modèles étudiés.

• GNNWR(TD) : modèle GNNWR utilisant le temps de trajet comme mesure de proximité.

Plus précisément, dans les zones dotées de paysages naturels et d'infrastructures complexes, telles que la rive ouest du lac Tangxun dans le district de Jiangxia, la rive du lac Hougong dans le district de Caidian et le confluent du fleuve Han et du fleuve Yangtze, et dans les zones de développement émergentes dotées de réseaux routiers bien développés et de grandes différences entre la proximité spatiale réelle et la distance physique, telles que les districts de Hongshan et de Xinzhou,Le résidu du modèle osp-GNNWR est significativement plus petit que celui des autres modèles, ce qui montre une précision de prédiction plus élevée.

Dans l’ensemble, les résultats de cette étude soulignent l’efficacité de l’OSP pour améliorer la capacité du modèle osp-GNNWR à représenter l’hétérogénéité spatiale, faisant ainsi progresser la modélisation des relations spatiales complexes au sein des marchés immobiliers.

L'apprentissage profond aide à résoudre les problèmes complexes de prévision des prix de l'immobilier

L’exploration des causes et des mécanismes d’influence de la différenciation spatiale des prix de l’immobilier est d’une grande importance pour maintenir le développement stable du marché immobilier et améliorer l’urbanisme et la satisfaction résidentielle. Cependant, la prévision du prix des logements est une question très complexe, impliquant de nombreux facteurs, tels que la situation géographique, la commodité des transports, le district scolaire, l'âge de la maison, le type de maison, etc. Les méthodes traditionnelles sont souvent basées sur des statistiques et l'apprentissage automatique, mais ces méthodes ont du mal à faire face à la taille et à la complexité croissantes des données. L’apprentissage profond dispose de puissantes capacités d’apprentissage et de classification des fonctionnalités et peut mieux gérer ces problèmes.

Afin d’améliorer la précision des prévisions des prix des logements, les recherches du secteur sont principalement menées dans les directions suivantes :

L’une d’elles est l’approche du modèle mixte.Il s’agit de combiner les méthodes d’apprentissage profond et d’apprentissage automatique traditionnelles pour exploiter pleinement leurs avantages respectifs. Par exemple, l’apprentissage profond peut être combiné avec des méthodes d’apprentissage automatique traditionnelles telles que les machines à vecteurs de support (SVM) ou les forêts aléatoires pour créer un modèle hybride de prévision des prix des logements.

La deuxième consiste à prendre en compte les données de séries chronologiques.Autrement dit, dans la prévision des prix des logements, en plus de prendre en compte les propriétés statiques de la maison, des données de séries chronologiques peuvent également être prises en compte, telles que les prix historiques des logements, les indicateurs économiques, etc., et des méthodes telles que les réseaux neuronaux récurrents (RNN) peuvent être utilisées pour l'analyse et la prédiction.

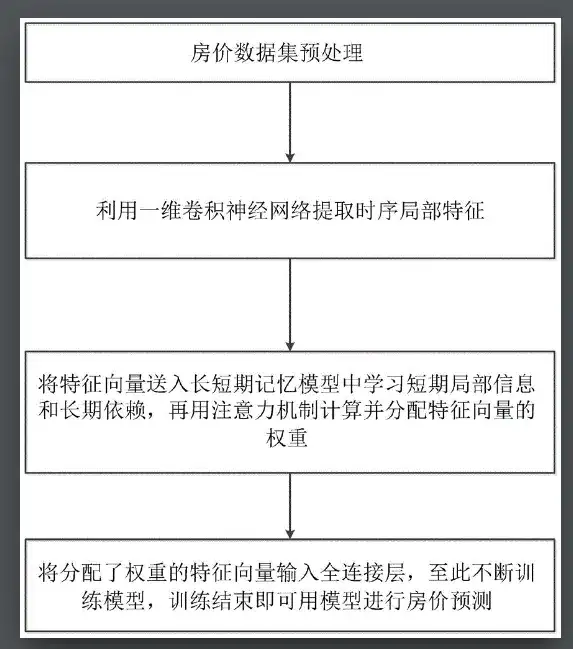
Par exemple,Certains chercheurs ont introduit une méthode de prédiction des prix des maisons par séries chronologiques convolutionnelles basée sur le mécanisme d'attention dans les brevets de Google.Les chercheurs ont d’abord prétraité l’ensemble de données sur les prix des logements et ont obtenu une série chronologique de facteurs multidimensionnels liés aux prix des logements.

En tenant compte des facteurs multidimensionnels connexes qui affectent les prix des logements, des fluctuations et des impacts sur les tendances des prix des logements, un réseau neuronal de séries temporelles convolutives basé sur le mécanisme d'attention est utilisé pour prédire les prix des logements. Un réseau neuronal convolutif unidimensionnel est utilisé pour traiter les caractéristiques des facteurs liés multidimensionnels afin d'obtenir un vecteur de caractéristiques multidimensionnel après une extraction de caractéristiques supplémentaire et une réduction de dimensionnalité. Le vecteur de caractéristiques est ensuite introduit dans le modèle de mémoire à long terme pour connaître la tendance globale à long terme et les informations de dépendance locale à court terme entre les caractéristiques.

Cette méthode combine la tendance générale à long terme et les informations locales à court terme des prévisions de séries chronologiques des prix des logements, réduit la variance des prévisions de prix des logements et améliore la capacité de généralisation des méthodes de prévision des prix des logements basées sur des données de séries chronologiques multidimensionnelles.

La troisième est l’application du Système d’Information Géographique (SIG).Combinez l’apprentissage profond avec les systèmes d’information géographique (SIG) pour analyser l’impact de facteurs tels que la situation géographique sur les prix des logements et améliorer la précision de prédiction du modèle – le modèle osp-GNNWR mentionné ci-dessus en est un exemple typique.

Avec le soutien de l’IA, le modèle de prévision des prix des logements deviendra plus fiable et plus précis. Sur cette base, les sociétés immobilières peuvent réduire les risques d’investissement ; Le gouvernement peut contrôler pleinement et précisément les informations sur le logement, afin de mener une gestion ciblée, de créer conjointement un bon environnement immobilier et d'aider les gens à vivre et à travailler véritablement dans la paix et la satisfaction.

Références :
1.https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2343771
2.https://mp.weixin.qq.com/s/P4nk5sl2v60Q5DeVrOfWLw
3.https://cloud.baidu.com/article/1892933
4.https://patents.google.com/pate