Command Palette
Search for a command to run...
L'article De l'Institut Des semi-conducteurs De l'Académie Chinoise Des Sciences a Été Publié À Nouveau Dans La Revue De Référence Du TNNLS, Apportant Une Nouvelle Perspective Sur l'exploration Des Expressions mathématiques.
La résolution d’expressions mathématiques est un sujet de recherche très important dans le domaine de l’apprentissage automatique, et la régression symbolique (SR) est une méthode permettant de trouver des expressions mathématiques précises à partir de données.
La régression symbolique est utilisée pour révéler l’expression mathématique sous-jacente de données d’observation données. Il possède une capacité naturelle à expliquer et à généraliser, et peut expliquer les mécanismes causaux entre les variables ou prédire les tendances de développement de systèmes complexes. Il est également largement utilisé dans différents domaines tels que la physique et l’astronomie.
Un cas d’application célèbre est la découverte par Kepler des orbites des planètes. Les scientifiques ont utilisé des algorithmes de régression symbolique pour découvrir de nouvelles lois du mouvement céleste et ainsi déduire leurs orbites. Il s’agit d’une contribution importante à l’exploration humaine de la vaste mer d’étoiles de l’univers.
Cependant, la recherche sur la régression symbolique présente également ses propres difficultés. La régression symbolique se concentre sur l'obtention de la meilleure combinaison de ces éléments et sur la résolution des coefficients les plus appropriés étant donné les variables indépendantes X et la variable dépendante Y. Cependant, l'obtention de la meilleure combinaison est un problème NP-difficile (polynôme non déterministe), et l'espace de combinaison croît exponentiellement avec la longueur de l'expression symbolique. De plus, le processus de résolution non linéaire des coefficients et le processus d'optimisation de la combinaison d'éléments interfèrent l'un avec l'autre, il est donc très long de déterminer l'expression exacte.
En réponse à ce problème académique,Des chercheurs de l'Institut des semi-conducteurs de l'Académie chinoise des sciences ont considéré la solution de la structure d'expression comme un problème de classification et l'ont résolu grâce à l'apprentissage supervisé, en proposant un réseau symbolique appelé DeepSymNet pour représenter les expressions symboliques.Comparé à plusieurs algorithmes SR populaires basés sur l'apprentissage supervisé, DeepSymNet utilise des étiquettes plus courtes, réduit l'espace de recherche de prédiction et améliore la robustesse de l'algorithme.

Adresse du document :
https://ieeexplore.ieee.org/document/10327762
Suivez le compte officiel et répondez « DeepSymNet » pour télécharger le document
Les limites des méthodes existantes mises en évidence
Il existe deux principaux types de solutions à la structure d'expression symbolique actuellement populaire :
- Solutions basées sur la recherche
La solution classique basée sur la recherche est l’algorithme GP (programmation génétique). Tout d’abord, de nombreuses expressions sont obtenues de manière aléatoire en tant que population initiale, puis l’évolution est réalisée par réplication, échange et mutation, et la progéniture avec une qualité moindre est sélectionnée pour continuer à évoluer jusqu’à ce que l’expression réponde à l’exigence de qualité.
En outre, parmi les méthodes basées sur la recherche, une classe importante de méthodes consiste à utiliser l'apprentissage par renforcement pour rechercher des structures d'expression appropriées, telles que l'algorithme DSR, qui code l'arbre de symboles sous forme de séquence et utilise la méthode du gradient de politique dans l'apprentissage par renforcement profond pour le résoudre. L’idée derrière DSR est d’augmenter la probabilité d’échantillonner des expressions avec des récompenses plus importantes, produisant ainsi des expressions avec des erreurs plus petites.
Il existe également un algorithme SR pour les formules physiques - AIFeynman, qui utilise principalement les connaissances préalables en physique pour juger la structure de l'expression, décomposant ainsi l'expression en sous-problèmes plus petits et réduisant l'espace de recherche ; une autre méthode basée sur l'optimisation parcimonieuse - EQL, utilise principalement l'algorithme BP combiné à l'optimisation parcimonieuse pour apprendre les paramètres, obtenant ainsi un sous-réseau parcimonieux dans le réseau EQL, puis obtenant la structure d'expression mathématique.
Outre leurs propres défauts évidents, ce type de méthode présente l’inconvénient commun d’être lent car l’espace de recherche est grand et l’expérience de solution ne peut pas être réutilisée.
- Solutions basées sur l'apprentissage supervisé
Les solutions basées sur l’apprentissage supervisé peuvent surmonter les lacunes chronophages des solutions basées sur la recherche. Les méthodes représentatives incluent SymbolicGPT, NeSymReS et E2E.
* SymbolicGPT encode les expressions symboliques en chaînes et considère la solution de structure d'expression comme une tâche de traduction de langue. Le modèle GPT dans le processus de traduction linguistique utilise un grand nombre d’échantillons générés artificiellement pour la formation supervisée ;
* NeSymReS encode l'arbre de symboles sous forme de séquence via une traversée pré-commandée et l'entraîne à l'aide de l'ensemble Transformer ;
* E2E encode la structure d'expression et les coefficients dans des étiquettes pour la formation, prédisant ainsi simultanément la structure d'expression et les coefficients.
Cependant, ces solutions présentent des problèmes d’étiquettes multiples équivalentes et d’échantillons d’entraînement déséquilibrés, ce qui peut facilement provoquer une ambiguïté pendant le processus d’entraînement et affecter la robustesse de l’algorithme.De plus, ils présentent d’autres défauts. Par exemple, SymbolicGPT considère des expressions relativement simples car le nombre de symboles utilisés pour l’échantillonnage est au maximum de quatre couches ; E2E encode les coefficients sous forme d'étiquettes, ce qui rend les étiquettes très longues et affecte la précision de la prédiction, etc.
Une nouvelle approche pour résoudre les problèmes - DeepSymNet
Des chercheurs de l'Institut des semi-conducteurs de l'Académie chinoise des sciences ont proposé un nouveau réseau symbolique appelé DeepSymNet pour représenter les expressions symboliques et ont présenté le cadre global de DeepSymNet.La première couche est celle des données, la couche intermédiaire est la couche cachée et la dernière couche est la couche de sortie.

Les nœuds de la couche cachée sont composés de symboles d'opération, notamment +, -, ×, ÷, sin, cos, exp, log, id, etc., où l'opérateur id est le même que l'opérateur id dans EQL.
Le nombre d'opérateurs d'identification dans chaque couche cachée est égal au nombre de nœuds dans la couche précédente, tandis que les autres opérateurs n'apparaissent qu'une seule fois dans chaque couche cachée. L'identifiant de l'opérateur correspond un à un au nœud de la couche précédente, ce qui permet à chaque couche d'utiliser toutes les informations de la couche précédente. Les autres opérateurs sont des opérateurs ordinaires et sont entièrement connectés à la couche précédente.
La connexion entre l'opérateur id et la couche précédente est fixe, et l'opérateur ordinaire n'a aucune connexion à la couche précédente, ou une ou deux connexions, ce qui signifie que dans ce réseau, un sous-réseau représente une expression symbolique. Plus une expression occupe de couches cachées, plus sa complexité est élevée. Par conséquent, le nombre de couches cachées peut être utilisé pour mesurer approximativement la complexité d’une expression.
Mais veuillez noter que la couche d'entrée possède un nœud spécial « const » qui est utilisé pour représenter des coefficients constants dans des expressions symboliques. Seuls les bords connectés aux nœuds « const » ont des poids (coefficients constants) pour empêcher qu'un nombre suffisant de coefficients constants n'apparaissent dans les expressions symboliques.
en tout,DeepSymNet est un réseau complet qui peut représenter n'importe quelle expression. La résolution de SR est le processus de recherche de sous-réseaux dans DeepSymNet.
Deux groupes de comparaisons expérimentales montrent les avantages
L’équipe de recherche a mené des tests basés sur des ensembles de données générés artificiellement et des ensembles de données publics, et a comparé les algorithmes actuellement populaires.
Adresse de téléchargement du jeu de données :
https://hyper.ai/datasets/29321
Dans l'expérience, DeepSymNet possède au plus 6 couches cachées et prend en charge au plus 3 variables. L’équipe de recherche a généré 20 échantillons pour chaque étiquette, chacun contenant 20 points de données. L'intervalle d'échantillonnage pour les coefficients constants et les variables est [-2,2]. La stratégie d’entraînement consiste à arrêter précocement (c’est-à-dire à arrêter l’entraînement lorsque la perte sur l’ensemble de validation ne diminue plus). Assisté par Adam Optimizer.
- Résultats des tests sur des données générées artificiellement
Les résultats des tests montrent :
* La difficulté de prédiction augmente à mesure que le nombre d’objets de prédiction augmente, et la couche cachée (c’est-à-dire la complexité) de l’expression augmente également ;
* Le goulot d’étranglement de la prédiction d’étiquettes réside dans le choix de l’opérateur ;
* DSN2 résout les solutions optimales et approximatives mieux que DSN1 ;
* La fusion d’étiquettes équivalentes et l’équilibrage des échantillons peuvent améliorer la robustesse de l’algorithme.
d'abord,DeepSymNet peut représenter des expressions plus efficacement que les arbres symboliques, et pour le même module qui apparaît plusieurs fois dans une expression, la longueur moyenne de l'étiquette de DeepSymNet est plus courte que celle de NeSymRes.

La précision de prédiction du modèle formé avec les étiquettes DeepSymNet dépasse de loin celle du modèle formé avec les étiquettes NeSymReS, comme le montre la figure ci-dessus. Cela montre que les étiquettes DeepSymNet sont meilleures que les étiquettes d’arbre symbolique.
Deuxièmement,À mesure que le nombre de couches cachées occupées par l’expression augmente, la précision de prédiction du modèle diminue rapidement. Par conséquent, l'équipe de recherche a proposé que la prédiction d'étiquettes puisse être divisée en deux sous-tâches : la prédiction d'opérateur et la prédiction de relation de connexion, afin de garantir que le problème de prédiction d'étiquettes puisse être mieux résolu.

Les résultats de la formation de DeepSymNet en deux parties montrent qu'à mesure que le nombre de couches cachées augmente, la précision de prédiction de la sélection des opérateurs diminue fortement, tandis que la précision de prédiction des relations de connexion reste élevée. Cela est dû au fait que l’espace de sélection de l’opérateur est beaucoup plus grand que l’espace de sélection de la relation de connexion. Par conséquent, afin d’améliorer la précision de la sélection des opérateurs, les chercheurs ont mené une formation distincte sur la sélection des opérateurs.

Au cours du processus de prédiction, l’équipe a d’abord utilisé le modèle de sélection d’opérateur pour obtenir la séquence de sélection d’opérateur, puis l’a saisie dans le modèle DSN1 formé pour prédire la relation de connexion. Les résultats du test sont présentés dans la figure ci-dessus. Après une formation distincte sur la sélection des opérateurs, la précision des prédictions s’est considérablement améliorée. Le modèle formé séparément est appelé DSN2.
De plus, les chercheurs ont mené des expériences d’ablation pour vérifier la robustesse de la fusion d’étiquettes équivalentes et de l’amélioration de l’équilibrage des échantillons. Tout d’abord, 500 000 échantillons d’entraînement ont été sélectionnés au hasard, contenant 128 455 étiquettes différentes (TrainDataOrg). Les résultats montrent que les numéros d'échantillons de ces étiquettes sont distribués de manière très inégale, le numéro d'échantillon minimum étant de 1, le numéro d'échantillon maximum étant de 13 196 et la variance du numéro d'échantillon étant de 13 012,29.

L'équipe a ensuite équilibré le nombre d'échantillons pour obtenir des échantillons d'entraînement TrainDataB et des échantillons d'entraînement TrainDataBM après avoir fusionné des étiquettes équivalentes.
Ensuite, sur la base des trois données d’entraînement, les modèles DSNOrg, DSNB et DSNBM ont été obtenus. Ces trois modèles ont été testés sur l’ensemble de test. La précision des trois modèles a augmenté du début à la fin.Cela montre qu'après avoir augmenté l'équilibre de l'échantillon et fusionné les étiquettes équivalentes, la précision du modèle dans la recherche de la solution optimale a été améliorée, ce qui a en effet renforcé la robustesse de l'algorithme et amélioré les performances de l'algorithme.
- Résultats des tests de l'ensemble de données publiques
L'équipe de recherche a utilisé 6 ensembles de données de test :Koza Korns, Keijzer, Vlad, ODE et AIFeynman ont sélectionné des expressions ne comportant pas plus de 3 variables à partir de ces ensembles de données pour les tests. La comparaison avec les méthodes d’apprentissage supervisé actuellement populaires montre que la précision des algorithmes proposés (DSN1, DSN2) est supérieure à celle des algorithmes de comparaison.
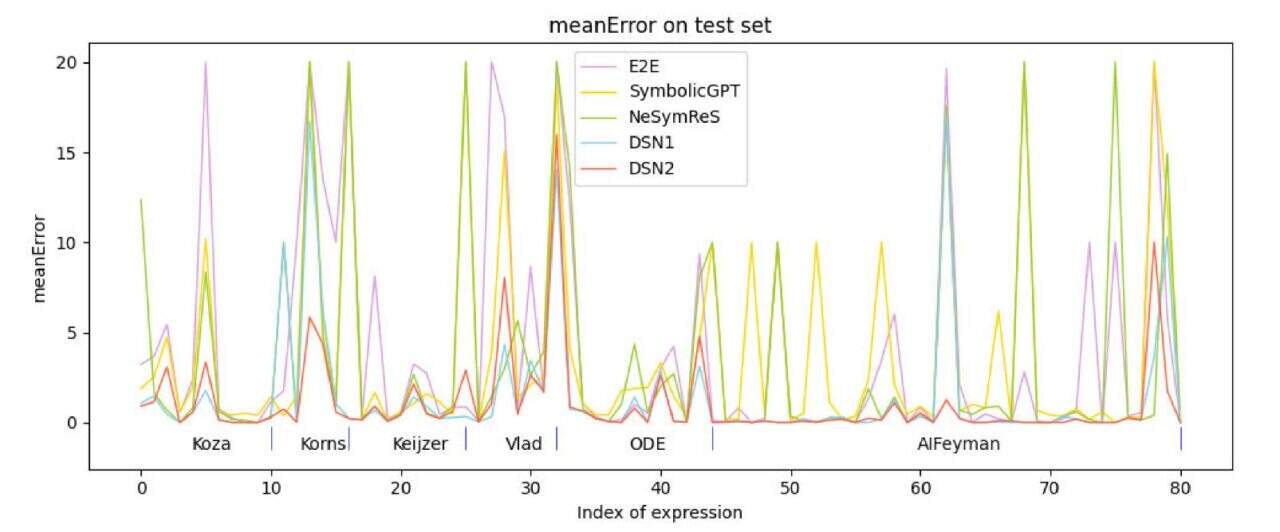
De plus, l’équipe a comparé l’algorithme avec les méthodes de recherche actuellement populaires EQL, GP et DSR, et les résultats sont présentés dans la figure ci-dessous.
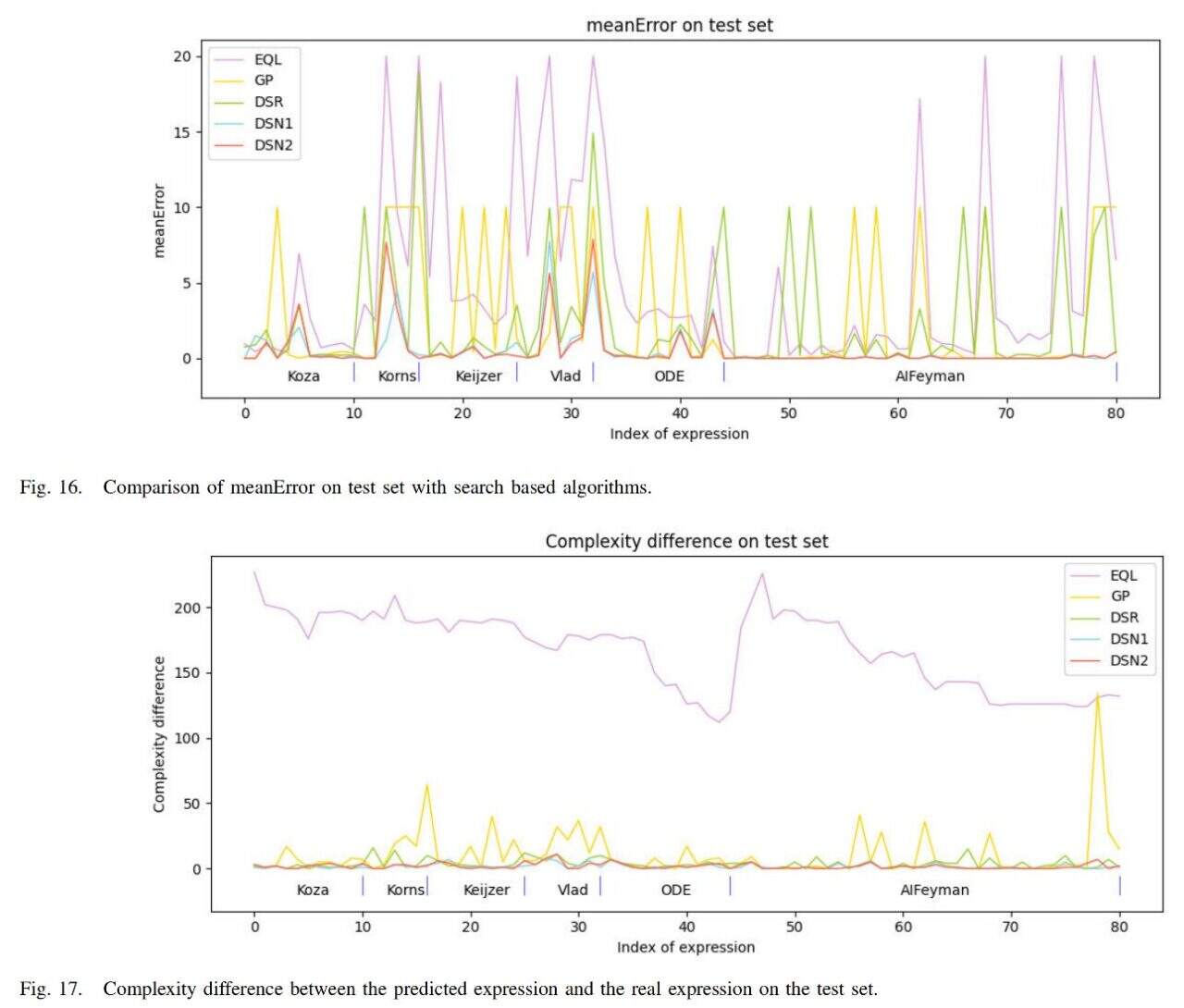
L'erreur moyenne de l'algorithme (DSN1, DSN2) est la plus petite et la complexité de l'expression obtenue est également la plus proche de la complexité de l'expression vraie.
En résumé, sur la base des résultats, on peut conclure queL'algorithme étudié par l'équipe surpasse les algorithmes comparatifs dans trois aspects : l'erreur d'expression symbolique, la complexité de l'expression symbolique et la vitesse d'exécution, ce qui confirme l'efficacité de l'algorithme.
L'équipe en coulisses est composée de stars
Les scientifiques du monde entier travaillent d’arrache-pied sur les questions fondamentales de la régression symbolique. Bien que l’article mentionne que DeepSymNet présente encore certaines limites, cette recherche apporte néanmoins une contribution importante à l’intelligence artificielle dans la résolution de problèmes mathématiques. En le traitant comme un problème de classification, il fournit sans aucun doute une nouvelle solution pour les méthodes SR basées sur l'apprentissage supervisé.
Bien sûr, cette réussite est indissociable de la passion et de la sueur d’un groupe de personnes, comme Wu Min, le premier auteur de l’article. Selon le site officiel de l'Institut des semi-conducteurs de l'Académie chinoise des sciences,Wu Min est actuellement chercheur adjoint à l'Institut des semi-conducteurs de l'Académie chinoise des sciences. Il a participé à plusieurs projets de recherche scientifique, notamment « Régression symbolique basée sur l'apprentissage profond et son application dans la recherche et le développement de dispositifs semi-conducteurs » et « Méthode de régression symbolique de simplification par division et conquête du réseau neuronal de fusion des connaissances ».
en outre,Le Dr Jingyi Liu, l'un des auteurs de l'article, a été le premier auteur d'un article publié dans la revue de pointe sur l'intelligence artificielle Neural Networks en juillet de l'année dernière. L'article s'intitulait « SNR : Cadre d'apprentissage rectifiable basé sur un réseau symbolique pour la régression symbolique ».Un cadre d’apprentissage avec des capacités de correction est fourni pour le problème de régression symbolique.
À en juger par les recherches sur des sujets connexes, le pays est résolument à la pointe des méthodes innovantes. On peut s’attendre à ce que ces théories et ces résultats de recherche apportent certainement des contributions importantes à la résolution de problèmes pratiques dans un avenir proche.