Command Palette
Search for a command to run...
AlphaGeometry : La Puissance De Calcul Massive De DeepMind Crée À Nouveau Des Miracles, Mais « La Puissance De Calcul Au Lieu De l'intelligence » n'est Peut-être Pas La Solution Optimale

Auteur : Li Baozhu
Rédacteur en chef : Sanyang
Source de l'image de couverture : Google DeepMind
DeepMind utilise la puissance de calcul pour créer des miracles ? Quelle est la valeur du très apprécié AlphaGeometry ?
Récemment, la série Alpha de Google DeepMind a ajouté un nouveau membre - AlphaGeometry, qui est toujours très populaire, avec des éloges tels que « étape importante », « épique » et « proche des humains » débordant de l'écran. Alors, quelle est la valeur de ce système d’IA, qui prétend avoir des capacités dignes d’une médaille d’or aux Olympiades mathématiques ?
AlphaGeometry a été développé par l'équipe Google DeepMind et des chercheurs de l'Université de New York.Combinaison d'un modèle de langage neuronal avec un moteur de déduction symbolique,Capable de résoudre des problèmes de géométrie complexes à un niveau proche de celui des humains.
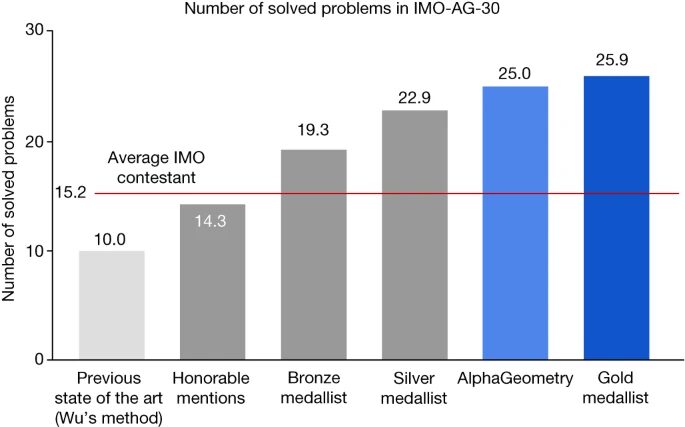
Lors d'un test de référence portant sur 30 problèmes de géométrie de l'Olympiade mathématique internationale (IMO), AlphaGeometry en a résolu 25 dans le temps imparti, qui était auparavant SOTA La « méthode Wu » de Wu a permis de résoudre 10 problèmes, tandis que le médaillé d'or humain de l'OMI a pu résoudre en moyenne 25,9 problèmes.
En effet, depuis le lancement d'AlphaGo, accompagné de nombreuses avancées innovantes dans différentes disciplines, le positionnement « les produits DeepMind doivent être de haute qualité » s'est progressivement ancré dans les esprits. Mais en même temps, il y a aussi des voix rationnelles et dialectiques dans l'industrie : le remplacement de l'intelligence par la puissance de calcul est certainement gratifiant, mais la valeur réelle de l'application est plus importante. Par conséquent, avec la sortie d'AlphaGeometry, nous aimerions discuter brièvement s'il s'agit d'un carnaval sous l'avantage de la puissance de calcul, ou L'IA pour la science Éclaireur.
Il convient de mentionner queNous avons interviewé le professeur de l'École du renseignement de l'Université de PékinLin Zhouchen, et discuté et étudié des questions académiques pertinentes.Le professeur Lin Zhouchen a étudié les mathématiques et les mathématiques appliquées à l'Université de Nankai, à l'Université de Pékin et à l'Université polytechnique de Hong Kong, puis est retourné à l'École de mathématiques de l'Université de Pékin pour poursuivre un doctorat et a commencé à entrer dans le domaine de l'intelligence artificielle. (Cliquez ici pour voir l'interview du professeur Lin Zhouchen)
Expression et calcul : deux défis majeurs de l'IA pour les mathématiques
Le professeur Lin Zhouchen a déclaré :« Dans le passé, l’expression de théorèmes mathématiques et le calcul à grande échelle étaient les deux principaux défis de l’IA pour prouver des théorèmes mathématiques. »
« Tout d'abord, en tant que matière très abstraite qui repose fortement sur le raisonnement logique, la première étape pour que les mathématiques adoptent l'IA consiste à résoudre le problème de l'« expression ». Exprimer des théorèmes mathématiques de manière à ce qu'ils soient calculables par ordinateur est la base des applications ultérieures de l'IA. »
Les problèmes géométriques ciblés par AlphaGeometry sont relativement faciles à exprimer. L’émergence de la géométrie analytique et de la géométrie algébrique a permis d’exprimer des formes géométriques et la relation entre des objets géométriques à travers des valeurs numériques.Wu WenjunLe "mécanisation mathématique", et dans une certaine mesure, il a également construit un pont entre les théorèmes de géométrie plane et le langage machine. "
Deuxièmement, la méthode Wu proposée par l'académicien Wu Wenjun et les méthodes traditionnelles telles que la base de Gröbner ont théoriquement résolu le problème de la démonstration des théorèmes de géométrie plane, mais elles sont limitées par la puissance de calcul. Autrement dit, en raison de l'important volume de stockage et de calcul, notamment face à des problèmes de géométrie plane plus complexes, l'espace de travail croît de manière exponentielle, ce qui rend difficile la résolution de nombreuses problèmes complexes par les méthodes précédentes.
Le problème de la grande quantité de calcul n’est évidemment pas le principal obstacle pour DeepMind, qui dispose de moyens importants. La principale difficulté réside dans la manière d’éviter la croissance exponentielle de l’espace d’exploitation, et c’est là que les méthodes d’apprentissage automatique peuvent aider. "
Plus précisément, AlphaGeometry est formé sur 100 millions de points de données synthétiques, peut résoudre de manière autonome des défis géométriques complexes sans démonstrations humaines et générer des preuves lisibles par l'homme.
Comme le montre la figure ci-dessous, en prenant comme exemple le « théorème isocèle » qui est le plus familier aux élèves du primaire et du secondaire de mon pays, si vous voulez prouver que ∠ABC=∠BCA, vous devez d'abord convertir manuellement le problème en langage informatique, puis le saisir dans AlphaGeometry.
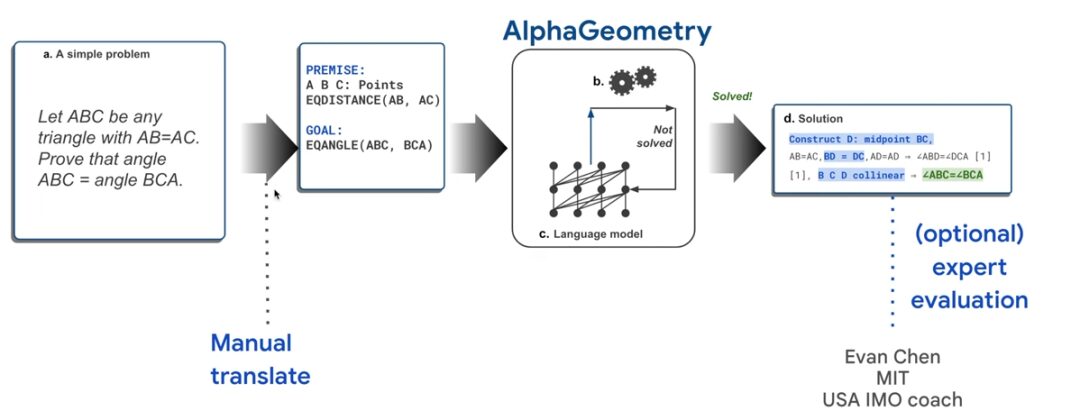
AlphaGeometry lance la recherche de preuves en exécutant un moteur de déduction symbolique qui déduit « de manière exhaustive » de nouvelles déclarations à partir des prémisses du théorème jusqu'à ce que le théorème soit prouvé ou que de nouvelles déclarations soient épuisées. Si le moteur de déduction symbolique ne parvient pas à trouver une preuve, le modèle de langage construit un point auxiliaire, ajoute des conditions prouvables et redémarre la recherche d'une preuve via le moteur symbolique. Ce cycle continue jusqu’à ce qu’une solution soit trouvée.
Les solutions seront automatiquement analysées dans un langage lisible par l’homme, afin qu’elles puissent être vérifiées et évaluées.
Il convient de mentionner qu'AlphaGeometry utilise des données synthétiques pour la formation des modèles, résolvant ainsi le problème du manque de bases de données pertinentes.
En utilisant le moteur symbolique existant sur diverses prémisses de théorèmes aléatoires et en l'exécutant sur 100 000 processeurs pendant 72 heures, les chercheurs ont obtenu environ 500 millions d'exemples de preuves de théorèmes synthétiques. Après normalisation formelle et déduplication, ils ont finalement obtenu 100 millions d'exemples de preuve de théorème, dont 9 millions d'exemples impliquaient au moins une construction auxiliaire, et de nombreuses étapes de preuve dépassaient 200, ce qui représente quatre fois la longueur moyenne de preuve des problèmes de géométrie dans l'Olympiade mathématique internationale.
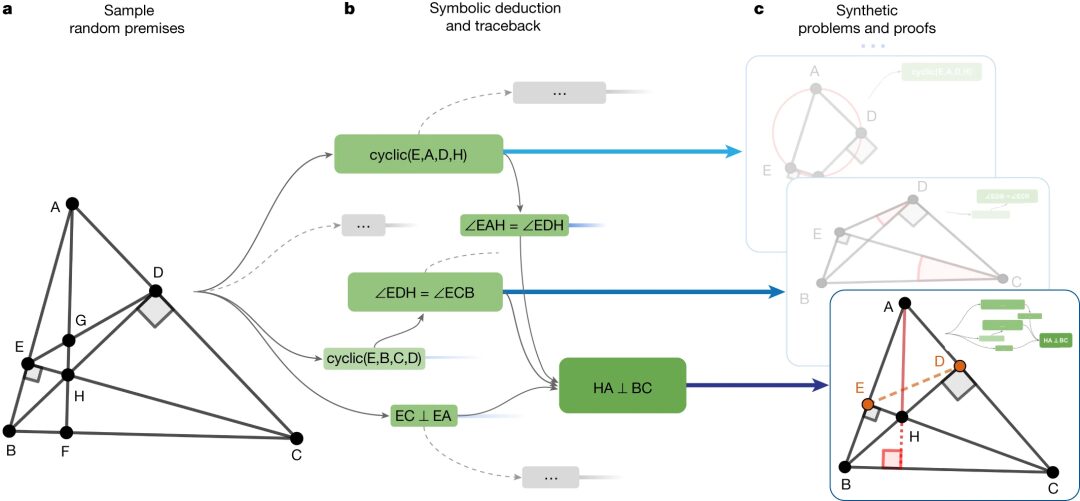
Afin de comparer et de tester la capacité d'AlphaGeometry à résoudre des problèmes pratiques, les chercheurs ont essayé de convertir les problèmes de géométrie du concours IMO depuis 2000 en langage machine lisible par les moteurs symboliques, et ont découvert que seul 75% pouvait être exprimé avec succès, formant ainsi un ensemble de test IMO-AG-30 composé de 30 problèmes de géométrie classiques.
Chaque problème a un temps d'exécution différent car la taille de sa fermeture de dérivation est différente. Les chercheurs ont constaté que le temps d’exécution n’était pas corrélé à la difficulté du problème. Par exemple, IMO 2019 P6 est beaucoup plus difficile que IMO 2008 P1a, mais nécessite beaucoup moins de temps de parallélisation pour être résolu dans le délai IMO.
Étant donné que le processus de décodage du modèle de langage renvoie k séquences différentes, décrivant k structures auxiliaires facultatives, les chercheurs ont effectué une recherche de faisceau sur les k options, en utilisant le score de chaque faisceau comme fonction de valeur. Cette méthode présente un fort parallélisme et peut grandement améliorer la vitesse de recherche lorsque des ressources de calcul parallèle sont disponibles.
Les chercheurs ont découvert que le nombre minimum de processeurs parallèles requis pour résoudre les 25 problèmes et rester dans la limite de temps avec quatre copies parallèles du modèle de langage accéléré GPU V100 est indiqué dans la figure suivante :
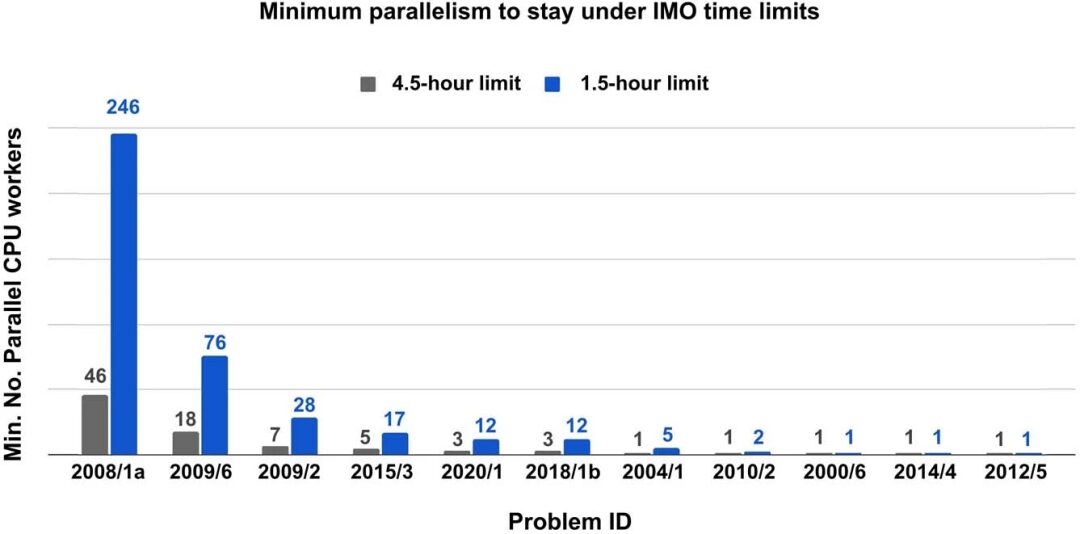
Les performances de 10 modèles/méthodes différents sur l’ensemble de tests IMO-AG-30 sont présentées dans la figure ci-dessous. Il est intéressant de noter que GPT-4 n’a pas eu une seule bonne réponse à une question du test.
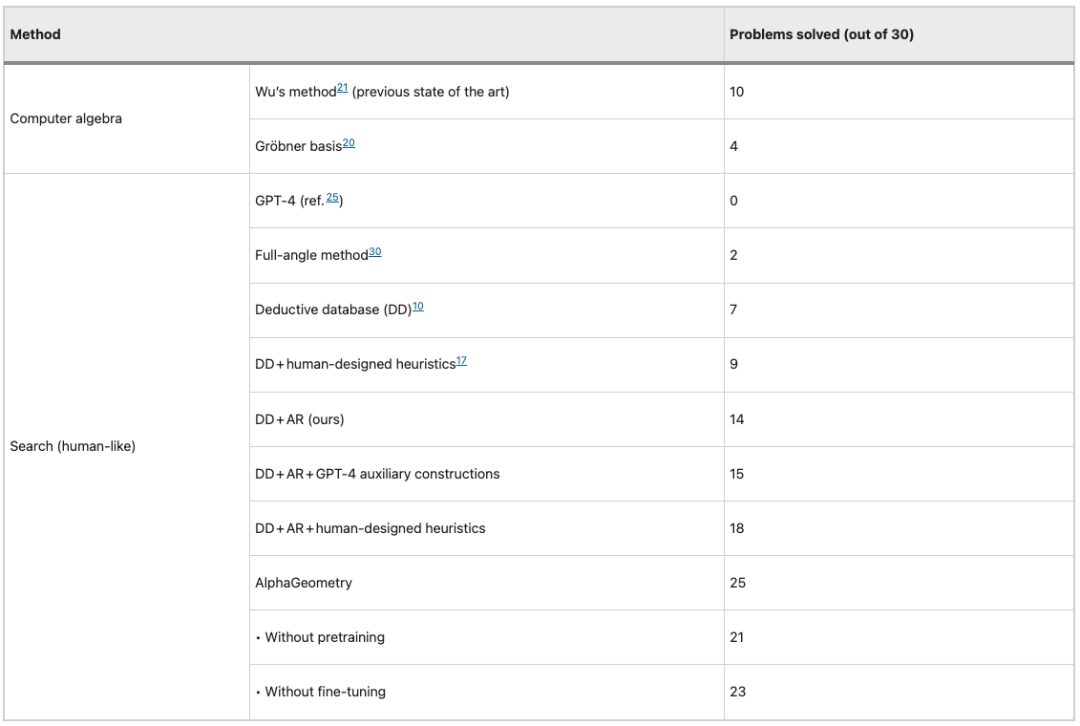
Derrière la substitution de la puissance de calcul à l'intelligence, la valeur de l'application est la clé
Au cours des deux derniers jours, les rapports accablants sur Internet ont pleinement révélé les réalisations d’AlphaGeometry. Son influence n’a pas besoin d’être élaborée, nous aimerions donc explorer, après le bruit, quelle valeur pratique AlphaGeometry peut apporter à la recherche scientifique et au développement d’applications d’IA ?
Le professeur Lin Zhouchen a déclaré :À l’heure actuelle, AlphaGeometry peut devenir un « enseignant » comme AlphaGo et jouer un rôle auxiliaire plus important dans l’enseignement.De plus, la percée d'AlphaGeometry en matière de performance des modèles est indéniable et démontre une fois de plus que « une grande puissance peut créer des miracles » : l'avantage de la puissance de calcul puissante crée de solides performances de modèle, ce qui, dans une certaine mesure, ajoute encore plus de confiance aux chercheurs et aux entreprises qui « vénèrent » la puissance de calcul. "
Cependant, comme l’a dit le professeur Lin Zhouchen,Dans le domaine de l'IA, bien que nous ayons été témoins à maintes reprises de l'efficacité de la « puissance de calcul remplaçant l'intelligence », la percée finale 1% pour devenir un expert de l'industrie est encore difficile à réaliser avec l'IA.
Ainsi, pour l'instant, qu'il s'agisse d'AlphaGeometry ou d'autres outils d'IA tels que le modèle GPT, ils restent « à la fois des enseignants et des amis » dans la vie quotidienne des gens et dans la recherche scientifique. L’utilisation flexible des outils d’IA est devenue une tendance générale. Comment appliquer le « miracle » créé par la puissance de calcul à des problèmes pratiques est une valeur des êtres humains difficile à remplacer.
Tirant les leçons du passé et les appliquant au présent, l’essor rapide des outils d’IA présente de nombreuses similitudes avec la popularisation des ordinateurs. Par exemple, il a révolutionné notre façon de travailler, remplaçant les méthodes traditionnelles avec une grande ampleur et devenant progressivement un critère d'évaluation des capacités sur le lieu de travail... Mais en revanche, les limites des outils d'IA sont également plus importantes, c'est-à-dire la spécificité.
Le professeur Lin Zhouchen estime que :Les outils d’IA actuels manquent d’uniformitéMême si l’on se concentre uniquement sur les mathématiques, il existe une grande différence entre les outils d’IA développés pour la théorie des nombres et la géométrie, sans parler des outils d’IA interdisciplinaires. Les outils d’IA ne sont pas encore aussi accessibles que l’infrastructure fondamentale que constituent les ordinateurs aujourd’hui. Les langages informatiques actuels incluent C, Java, Python, etc. Il est tout à fait possible de résoudre des problèmes dans plusieurs disciplines telles que les mathématiques, la physique, la chimie, etc. en se basant sur l'un de ces langages, ce qui reflète sa polyvalence. Cependant, ce n’est pas le cas avec les outils d’IA, comme le montre la série Alpha. "
Par conséquent, le professeur Lin Zhouchen estime que : « À l’avenir, lorsque les outils d’IA pourront être abstraits et réutilisés, l’IA pour la science pourra devenir populaire. » "
Il s’agit également d’un phénomène qu’HyperAI a observé en suivant en permanence le développement de l’IA pour la science. Certains groupes de recherche ou équipes de recherche recruteront un membre spécialisé en IA en plus des membres de la discipline pour être responsable du développement des outils d'IA nécessaires à la recherche, tandis que la partie Science est toujours laissée aux chercheurs scientifiques traditionnels.
Il ne fait aucun doute que l’aide et l’amélioration de l’IA dans le processus de recherche scientifique sont devenues de plus en plus évidentes et deviennent une nouvelle tendance, mais ce modèle d’équipe IA + Science est-il une solution à long terme ?
Le professeur Lin Zhouchen estime : « À l'avenir, d'une part, le seuil d'utilisation des outils d'IA doit être abaissé et un certain degré d'uniformité doit être atteint, afin que les scientifiques puissent également combiner et utiliser les composants des outils d'IA pour différents problèmes, tout comme la programmation informatique ; d'autre part, les scientifiques doivent également améliorer progressivement leur capacité à utiliser les outils d'IA afin de tirer pleinement parti de la puissance de l'IA. »
La route est longue et difficile, mais si vous continuez, vous atteindrez votre destination. L’IA pour la science a été initiée par de grandes entreprises telles que DeepMind, et avec la promotion des politiques nationales, elle a commencé un long voyage. Les épines du chemin doivent être éliminées par la recherche scientifique et l’industrie ensemble pour créer véritablement de la valeur pour le développement humain dans sa mise en œuvre.
Enfin, je voudrais remercier le professeur Lin Zhouchen de l’École du renseignement de l’Université de Pékin pour son aide et son soutien dans la rédaction de cet article. Actuellement, le groupe de recherche du professeur Zhouchen Lin recrute des doctorants. Les étudiants qui répondent aux exigences sont invités à envoyer leur CV à : [email protected]
Je vis selon le credo du physicien Ludwig Boltzmann : rien n’est plus pratique qu’une bonne théorie. Je recherche actuellement des doctorants forts en mathématiques (mais cela ne signifie pas que vous devez être issu d'un département de mathématiques) et très intéressés par l'analyse théorique, afin qu'ils puissent apprécier avec moi comment utiliser élégamment les mathématiques pour résoudre des problèmes pratiques. N'hésitez pas à m'envoyer votre CV.
——Lin Zhouchen